Bird J. Electrical Circuit Theory and Technology

Подождите немного. Документ загружается.

428 Electrical Circuit Theory and Technology

Powers and roots of complex numbers

In problems 32 to 35, evaluate in cartesian and in polar form.

32 (a) 2 C j3

(b) 4 j5

[(a) 5 C j12; 13

112

(b) 9  j40; 41

102

]

33 (a) 3 C j2

(b) 2  j

[(a) 597 C j122; 609.3

(b)  2  j11; 11.18

100

]

34 (a) 4



(b) 2

125



[(a)  157.6 C j201.7I 256

128

(b)  2.789  j31.88I32

95

]

35 (a) 3

/3

(b) 1.5

160



[(a) 27 C j0; 27

 (b) 0.8792 C j4.986; 5.063

]

In problems 36 to 38, determine the two square roots of the given

complex numbers in cartesian form and show the results on an

Argand diagram.

36 (a) 2 C j (b) 3  j2

[(a) š1.455 Cj0.344 (b) š1.818  j0.550]

37 (a) 3 C j4(b)1  j3 [(a) š1 Cj2 (b) š1.040  j1.442]

38 (a) 5

(b) 14

3/2

[(a) š2.127 Cj0.691 (b) š2.646 C j2.646]

39 Convert 2  j into polar form and hence evaluate 2  j

in polar

form. [

26

; 279.5

174

]

24 Application of complex

numbers to series a.c.

circuits

At the end of this chapter you should be able to:

ž appreciate the use of complex numbers in a.c. circuits

ž perform calculations on series a.c. circuits using complex

numbers

24.1 Introduction

Simple a.c. circuits may be analysed by using phasor diagrams. However,

when circuits become more complicated analysis is considerably simpli-

ﬁed by using complex numbers. It is essential that the basic operations

used with complex numbers, as outlined in Chapter 23, are thoroughly

understood before proceeding with a.c. circuit analysis. The theory intro-

duced in Chapter 15 is relevant; in this chapter similar circuits will be

analysed using j notation and Argand diagrams.

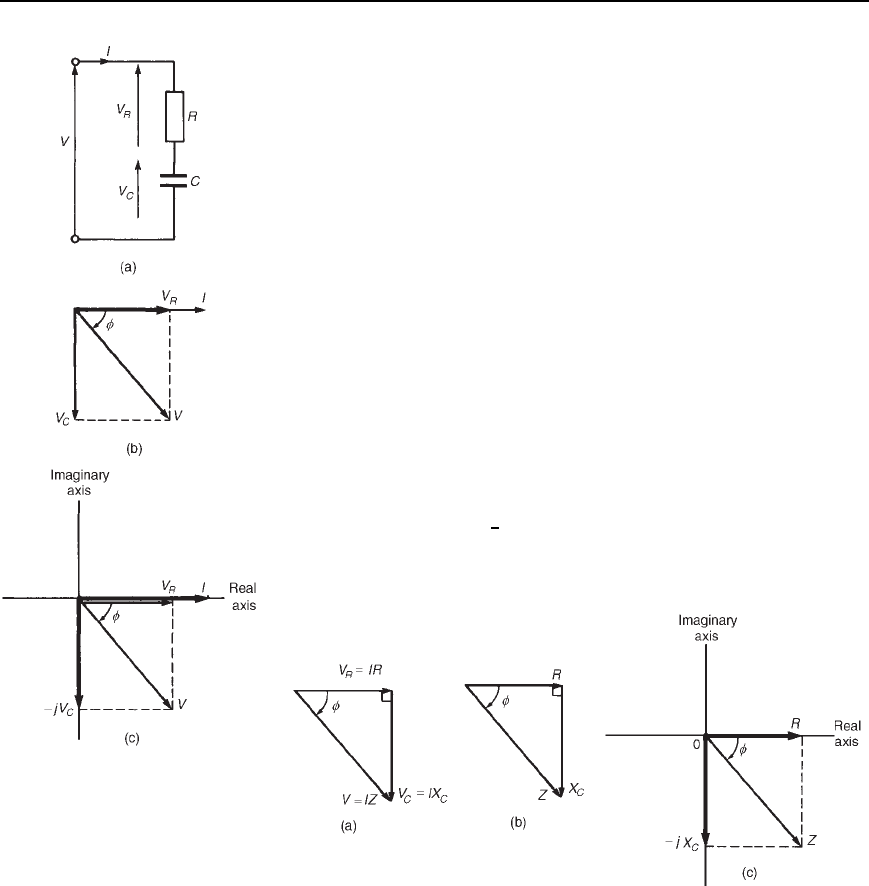
24.2 Series a.c. circuits

(a) Pure resistance

In an a.c. circuit containing resistance R only (see Figure 24.1(a)), the

current I

is in phase with the applied voltage V

as shown in the phasor

diagram of Figure 24.1(b). The phasor diagram may be superimposed on

the Argand diagram as shown in Figure 24.1(c). The impedance Z of the

circuit is given by

= R

(b) Pure inductance

In an a.c. circuit containing pure inductance L only (see Figure 24.2(a)),

the current I

lags the applied voltage V

by 90

as shown in the phasor

diagram of Figure 24.2(b). The phasor diagram may be superimposed on

the Argand diagram as shown in Figure 24.2(c). The impedance Z of the

circuit is given by

Z D

D X

or jX

Figure 24.1 (a) Circuit

diagram (b) Phasor diagram

430 Electrical Circuit Theory and Technology

Figure 24.1 Continued

where X

is the inductive reactance given by

= !L = 2pfL ohms,

where f is the frequency in hertz and L is the inductance in henrys.

In an a.c. circuit containing pure capacitance only (see Figure 24.3(a)),

the current I

leads the applied voltage V

by 90

as shown in the phasor

diagram of Figure 24.3(b). The phasor diagram may be superimposed on

the Argand diagram as shown in Figure 24.3(c). The impedance Z of the

circuit is given by

Z D

90

D X

−90

or −jX

where X

is the capacitive reactance given by

2pfC

ohms

where C is the capacitance in farads.



Note:  jX

j

ωC

jj

ωCj

j

jωC

1

jωC



(d) R–L series circuit

In an a.c. circuit containing resistance R and inductance L in series (see

Figure 24.4(a)), the applied voltage V is the phasor sum of V

and V

as shown in the phasor diagram of Figure 24.4(b). The current I lags

the applied voltage V by an angle lying between 0

and 90

—the actual

value depending on the values of V

and V

, which depend on the values

of R and L. The circuit phase angle, i.e., the angle between the current

and the applied voltage, is shown as angle  in the phasor diagram.

In any series circuit the current is common to all components and is

thus taken as the reference phasor in Figure 24.4(b). The phasor diagram

may be superimposed on the Argand diagram as shown in Figure 24.4(c),

where it may be seen that in complex form the supply voltage V is

given by:

= V

Y jV

Figure 24.5(a) shows the voltage triangle that is derived from the

phasor diagram of Figure 24.4(b) (i.e. triangle Oab). If each side of the

voltage triangle is divided by current I then the impedance triangle of

Figure 24.2 (a) Circuit

diagram (b) Phasor diagram

Application of complex numbers to series a.c. circuits 431

Figure 24.3 (a) Circuit

diagram (b) Phasor diagram

Figure 24.4 (a) Circuit diagram (b) Phasor diagram (c) Argand

diagram

Figure 24.5 (a) Voltage triangle (b) Impedance triangle (c) Argand

diagram

Figure 24.5(b) is derived. The impedance triangle may be superimposed

on the Argand diagram, as shown in Figure 24.5(c), where it may be seen

that in complex form the impedance Z is given by:

= R Y jX

Thus, for example, an impedance expressed as 3 Cj4 means that the

resistance is 3  and the inductive reactance is 4 

In polar form, Z DjZj

 where, from the impedance triangle, the

modulus of impedance jZjD



R

C X

 and the circuit phase angle

 D arctanX

/R lagging

(e) R–C series circuit

In an a.c. circuit containing resistance R and capacitance C in series

(see Figure 24.6(a)), the applied voltage V is the phasor sum of V

and

432 Electrical Circuit Theory and Technology

Figure 24.6 (a) Circuit

diagram (b) Phasor diagram

as shown in the phasor diagram of Figure 24.6(b). The current I

leads the applied voltage V by an angle lying between 0

and 90

—the

actual value depending on the values of V

and V

, which depend on

the values of R and C. The circuit phase angle is shown as angle  in

the phasor diagram. The phasor diagram may be superimposed on the

Argand diagram as shown in Figure 24.6(c), where it may be seen that

in complex form the supply voltage V is given by:

= V

− jV

Figure 24.7(a) shows the voltage triangle that is derived from the phasor

diagram of Figure 24.6(b). If each side of the voltage triangle is divided

by current I, the impedance triangle is derived as shown in Figure 24.7(b).

The impedance triangle may be superimposed on the Argand diagram as

shown in Figure 24.7(c), where it may be seen that in complex form the

impedance Z is given by

= R − jX

Thus, for example, an impedance expressed as 9 j14 means that

the resistance is 9  and the capacitive reactance X

is 14 

In polar form, Z DjZj

 where, from the impedance triangle,

jZjD



R

C X

 and  D arctanX

/R leading

Figure 24.7 (a) Voltage triangle (b) Impedance triangle (c) Argand

diagram

(f) R–L–C series circuit

In an a.c. circuit containing resistance R, inductance L and capacitance

C in series (see Figure 24.8(a)), the applied voltage V is the phasor sum

of V

, V

and V

as shown in the phasor diagram of Figure 24.8(b)

(where the condition V

is shown). The phasor diagram may be

superimposed on the Argand diagram as shown in Figure 24.8(c), where

Application of complex numbers to series a.c. circuits 433

Figure 24.8 (a) Circuit

diagram (b) Phasor diagram

it may be seen that in complex form the supply voltage V is given by:

= V

Y j.V

− V

From the voltage triangle the impedance triangle is derived and superim-

posing this on the Argand diagram gives, in complex form,

impedance Z

= R Y j.X

− X

/ or Z = jZj

where, jZjD



C X

 X



]and D arctanX

 X

/R

When V

D V

, X

D X

and the applied voltage V and the current

I are in phase. This effect is called series resonance and is discussed

separately in Chapter 28.

(g) General series circuit

In an a.c. circuit containing several impedances connected in series, say,

,...,Z

, then the total equivalent impedance Z

is given by

= Z

Y Z

Y ...Y Z

Problem 1. Determine the values of the resistance and the

series-connected inductance or capacitance for each of the

following impedances: (a) 12 C j5 (b) j40  (c) 30



(d) 2.20 ð 10

30

. Assume for each a frequency of 50 Hz.

(a) From Section 24.2(d), for an R –L series circuit, impedance

Z D R C jX

Thus Z D 12 C j5 represents a resistance of 12  and an induc-

tive reactance of 5  in series.

Since inductive reactance X

D 2fL,

inductance L D

2f

250

D 0.0159 H

i.e., the inductance is 15.9 mH.

Thus an impedance .12 Y j5/Z represents a resistance of 12 Z

in series with an inductance of 15.9 mH.

(b) From Section 24.2(c), for a purely capacitive circuit, impedance

Z DjX

Thus Z Dj40  represents zero resistance and a capacitive reac-

tance of 40 .

Since capacitive reactance X

D 1/2fC,

capacitance C D

2fX

25040

F D

25040

µF

D 79.6

µF

434 Electrical Circuit Theory and Technology

Thus an impedance −j40 Z represents a pure capacitor of

capacitance 79.6 mF

D 30cos60

C j sin60

 D 15 C j25.98

Thus Z D 30

 D 15 C j25.98 represents a resistance of

15  and an inductive reactance of 25.98  in series (from

Section 24.2(d)).

Since X

D 2fL,

inductance L D

2f

25.98

250

D 0.0827 H or 82.7mH

Thus an impedance 30

Z represents a resistance of 15 Z in

series with an inductance of 82.7 mH

(d) 2.20 ð 10

30

D 2.20 ð 10

[cos30

 C j sin30

]

D 1.905 ð 10

 j1.10 ð 10

Thus Z D 2.20 ð10

30

 D 1.905 ð 10

 j1.10 ð10

 re-

presents a resistance of 1.905 ð 10

 (i.e. 1.905 M) and a capac-

itive reactance of 1.10 ð10

 in series (from Section 24.2(e)).

Since capacitive reactance X

D 1/2fC,

capacitance C D

2fX

2501.10 ð 10



D 2.894 ð 10

9

F or 2.894 nF

Thus an impedance 2.2

× 10

−30

Z represents a resistance of

1.905 MZ in series with a 2.894 nF capacitor.

Problem 2. Determine, in polar and rectangular forms, the current

ﬂowing in an inductor of negligible resistance and inductance

159.2 mH when it is connected to a 250 V, 50 Hz supply.

Inductive reactance X

D 2fL D 250159.2 ð 10

3

 D 50 

Thus circuit impedance Z D 0 C j50 D 50



Supply voltage, V D 250

V (or (250 C j0)V)

(Note that since the voltage is given as 250 V, this is assumed to mean

250

Vor(250C j0)V)

Hence current I D

250

0

 90

 D 5

−90

Application of complex numbers to series a.c. circuits 435

Alternatively, I D

250 C j0

0 C j50

250j50

j50j50

j50250

D −j5A

which is the same as 5

90

Problem 3. A 3 µF capacitor is connected to a supply of frequency

1 kHz and a current of 2.83

A ﬂows. Determine the value of

the supply p.d.

Capacitive reactance X

2fC

210003 ð 10

6



D 53.05 

Hence circuit impedance Z D 0  j53.05 D 53.05

90



Current I D 2.83

A(or0 C j2.83A

Supply p.d., V D IZ D 2.83

53.05

90



i.e. p.d.

= 150

Alternatively, V D IZ D 0 C j2.830 j53.05

Dj

2.8353.05 D 150 V

Problem 4. The impedance of an electrical circuit is 30  j50

ohms. Determine (a) the resistance, (b) the capacitance, (c) the

modulus of the impedance, and (d) the current ﬂowing and its phase

angle, when the circuit is connected to a 240 V, 50 Hz supply.

(a) Since impedance Z D 30  j50, the resistance is 30 ohms and

the capacitive reactance is 50 

(b) Since X

D 1/2fC, capacitance,

C D

2fX

25050

D 63.66 mF



R

C X

 D



30

C 50



D 58.31 Z

(d) Impedance Z D 30  j50 D 58.31

arctan

D 58.31

59.04



Hence current I D

240

58.31

59.04

= 4.12

59.04

436 Electrical Circuit Theory and Technology

Figure 24.9

Problem 5. A 200 V, 50 Hz supply is connected across a coil

of negligible resistance and inductance 0.15 H connected in series

with a 32  resistor. Determine (a) the impedance of the circuit,

(b) the current and circuit phase angle, (c) the p.d. across the 32 

resistor, and (d) the p.d. across the coil.

(a) Inductive reactance X

D 2fL D 2500.15 D 47.1 

Impedance Z D R C jX

D .32 Y j47.1/Z or 57.0

55.81

The circuit diagram is shown in Figure 24.9

(b) Current I D

200

57.0

55.81

D 3.51

−55.81

i.e., the current is 3.51 A lagging the voltage by 55.81

D IR D 3.51

55.81

)32



i.e., V

= 112.3

−55.81

(d) P.d. across the coil, V

D IX

D 3.51

55.81

)47.1



i.e. V

= 165.3

34.19

The phasor sum of V

and V

is the supply voltage V as shown in the

phasor diagram of Figure 24.10.

D 112.3

55.81

D 63.11  j92.89 V

D 165.3

34.19

V D 136.73 C j92.89 V

Hence V D V

C V

D 63.11  j92.89 C 136.73 C j92.89

D 200 C j0 V or 200

V, correct to three signiﬁcant

ﬁgures.

Figure 24.10

Problem 6. Determine the value of impedance if a current

of 7 C j16A ﬂows in a circuit when the supply voltage is

(120 C j200)V. If the frequency of the supply is 5 MHz, determine

the value of the components forming the series circuit.

Impedance Z D

120 C j200

7 C j16

233.24

59.04

17.464

66.37

D 13.36

7.33  or 13.25  j1.705

The series circuit thus consists of a 13.25 Z resistor and a capacitor of

capacitive reactance 1.705 Z

Application of complex numbers to series a.c. circuits 437

Since X

2fC

, capacitance C D

2fX

25 ð 10

1.705

D 1.867 ð 10

8

F D 18.67 nF

Problem 7. For the circuit shown in Figure 24.11, determine the

value of impedance Z

Figure 24.11

Total circuit impedance Z D

3.5

20

D 20

 or 12.86 Cj15.32

Total impedance Z D Z

C Z

(see Section 24.2(g)).

Hence 12.86 C j15.32 D 4.36  j2.10 C Z

from which, impedance Z

D 12.86 C j15.32  4.36  j2.10

D .8.50 Y j17.42/Z or 19.38

63.99

Problem 8. A circuit comprises a resistance of 90  in series with

an inductor of inductive reactance 150 . If the supply current is

1.35

A, determine (a) the supply voltage, (b) the voltage across

the 90  resistance, (c) the voltage across the inductance, and

(d) the circuit phase angle. Draw the phasor diagram.

The circuit diagram is shown in Figure 24.12

(a) Circuit impedance Z D R C jX

D 90 C j150 or

174.93

59.04



Figure 24.12