Bird J. Electrical Circuit Theory and Technology
Подождите немного. Документ загружается.

418 Electrical Circuit Theory and Technology
D
10 Cj20
25
D
−10
25
Y j
20
25
or
− 0.4 Y j0.8
The elimination of the imaginary part of the denominator by multiplying
both the numerator and denominator by the conjugate of the denominator
is often termed ‘rationalizing’.
Problem 1. In an electrical circuit the total impedance Z
T
is
given by
Z
T
D
Z
1
Z
2
Z
1
C Z
2
C Z
3
Determine Z
T
in a C jb form, correct to two decimal places,
when Z
1
D 5 j3, Z
2
D 4 C j7andZ
3
D 3.9 j6.7
Z
1
Z
2
D 5 j34 C j7 D 20 C j35 j12 j
2
21
D 20 C j35 j12 C 21 D 41 C j23
Z
1
C Z
2
D 5 j3 C 4 C j7 D 9 C j4
Hence
Z
1
Z
2
Z
1
C Z
2
D
41 C j23
9 C j4
D
41 C j239 j4
9 C j49 j4
D
369 j164 C j207 j
2
92
9
2
C 4
2
D
369 j164 C j207 C92
97
D
461 C j43
97
D 4.753 C j0.443
Thus
Z
1
Z
2
Z
1
C Z
2
C Z
3
D 4.753 C j0.443 C 3.9 j6.7
D 8.65
− j6.26, correct to two decimal places.
Problem 2. Given Z
1
D 3 C j4andZ
2
D 2 j5 determine in
cartesian form correct to three decimal places:
(a)
1
Z
1
(b)
1
Z
2
(c)
1
Z
1
C
1
Z
2
(d)
1
1/Z
1
C 1/Z
2

Revision of complex numbers 419
(a)
1
Z
1
D
1
3 C j4
D
3 j4
3 C j43 j4
D
3 j4
3
2
C 4
2
D
3 j4
25
D
3
25
j
4
25
D 0.120
− j0.160
(b)
1
Z
2
D
1
2 j5
D
2 C j5
2 j52 C j5
D
2 C j5
2
2
C 5
2
D
2 C j5
29
D
2
29
C j
5
29
D 0.069 Y j0.172
(c)
1
Z
1
C
1
Z
2
D 0.120 j0.160 C 0.069 C j0.172
D 0.189 Y j0.012
(d)
1
1/Z
1
C 1/Z
2
D
1
0.189 Cj0.012
D
0.189 j0.012
0.189 C j0.0120.189 j0.012
D
0.189 j0.012
0.189
2
C 0.012
2
D
0.189 j0.012
0.03587
D
0.189
0.03587
j0.012
0.03587
D 5.269
− j0.335
Further problems on operations involving Cartesian complex numbers may
be found in Section 23.7, problems 1 to 11, page 424.
23.3 Complex equations
If two complex numbers are equal, then their real parts are equal and
their imaginary parts are equal. Hence, if a C jb D c C jd then a D c
and b D d. This is a useful property, since equations having two unknown
quantities can be solved from one equation. Complex equations are used
when deriving balance equations with a.c. bridges (see Chapter 27).
Problem 3. Solve the following complex equations:
(a) 3a C jb D 9 j2
(b) 2 C j2 Cj D x C jy
(c) a j2b C b j3a D 5 Cj2

420 Electrical Circuit Theory and Technology
(a) 3a C jb D 9 j2. Thus 3a C j3b D 9 j2
Equating real parts gives: 3a D 9, i.e. a
= 3
Equating imaginary parts gives: 3b D2, i.e., b
= −2=3
(b) 2 C j2 C j D x C jy
Thus 4 C j2 j2 C j
2
D x C jy
5 C j0 D x C jy
Equating real and imaginary parts gives: x
= −5, y = 0
(c) a j2b C b j3a D 5 C j2
Thus a C b C j2b 3a D 5 Cj2
Hence a C b D 5 1
and 2b 3a D 2 2
We have two simultaneous equations to solve. Multiplying equation
(1) by 2 gives:
2a C 2b D 10 3
Adding equations (2) and (3) gives a D 12, i.e. a
= −12
From equation (1), b
= 17
Problem 4. An equation derived from an a.c. bridge network is
given by
R
1
R
3
D R
2
C jωL
2
1
1/R
4
C jωC
R
1
, R
3
, R
4
and C
4
are known values. Determine expressions for R
2
and L
2
in terms of the known components.
Multiplying both sides of the equation by 1/R
4
C jωC
4
gives
R
1
R
3
1/R
4
C jωC
4
D R
2
C jωL
2
i.e. R
1
R
3
/R
4
C jR
1
R
3
ωC
4
D R
2
C jωL
2
Equating the real parts gives: R
2
= R
1
R
3
=R
4
Equating the imaginary parts gives:
ωL
2
D R
1
R
3
ωC
4
, from which, L
2
= R
1
R
3
C
4
Further problems on complex equations may be found in Section 23.7,
problems 12 to 16, page 425.
Revision of complex numbers 421
23.4 The polar form of a
complex number
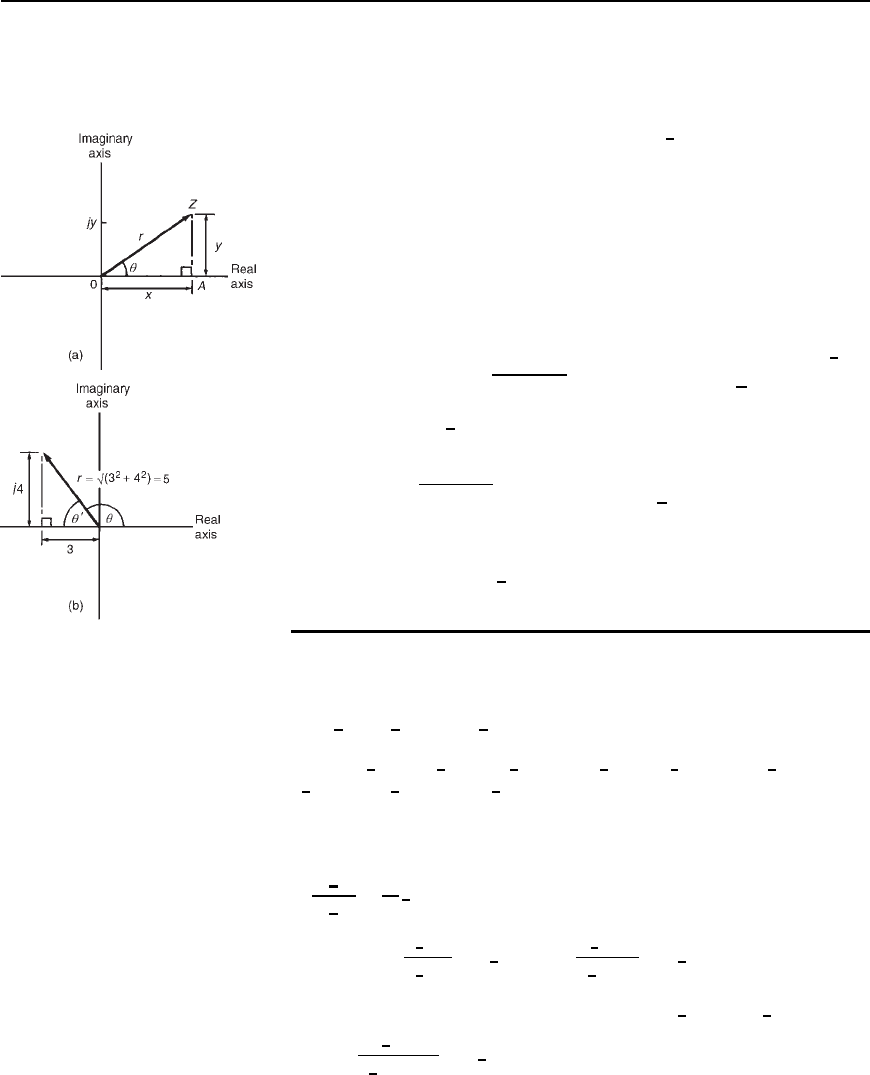
In Figure 23.3(a), Z D x Cjy D r cos C jr sin from trigonometry,
D rcos C j sin
This latter form is usually abbreviated to Z
= r
66
q, and is called the polar
form of a complex number.
r is called the modulus (or magnitude of Z) and is written as mod Z
or jZj. r is determined from Pythagoras’s theorem on triangle OAZ, i.e.
jZj
= r =
.x
2
Y y
2
/
The modulus is represented on the Argand diagram by the distance OZ.
is called the argument (or amplitude) of Z and is written as arg Z.
is also deduced from triangle OAZ: arg Z
= q = arctan y=x
For example, the cartesian complex number (3 Cj4) is equal to r
6
in
polar form, where r D
3
2
C 4
2
D 5 and q D arctan
4
3
D 53.13
°
Hence .3 Y j4/= 5
66
53.13
°
Similarly, (3 C j4) is shown in Figure 23.3(b),
where r D
3
2
C 4
2
D 5,
0
D arctan
4
3
D 53.13
°
and D 180
°
53.13
°
D 126.87
°
Hence .−3 Y j4/ = 5
66
126.87
°
Figure 23.3
23.5 Multiplication and
division using complex
numbers in polar form
(a) Multiplication
.r
1
66
q
1
/.r
2
66
q
2
/= r
1
r
2
66
.q
1
Y q
2
Thus 3
6
25
°
ð 2
6
32
°
D 6
6
57
°
,4
6
11
°
ð 5
6
18
°
D 20
6
7
°
,
2
6
/3 ð 7
6
/6 D 14
6
/2, and so on.
(b) Division
r
1
66
q
1
r
2
66
q
2
=
r
1
r
2
66
.q
1
Y q
2
/
Thus
8
6
58
°
2
6
11
°
D 4
6
47
°
,
9
6
136
°
3
6
60
°
D 3
6
136
°
60
°
D 3
6
196
°
or 3
6
164
°
,
and
10
6
/2
5
6
/4
D 2
6
3/4, andsoon.
Conversion from cartesian or rectangular form to polar form, and
vice versa, may be achieved by using the R ! P and P ! R conversion

422 Electrical Circuit Theory and Technology
facility which is available on most calculators with scientific notation.
This allows, of course, a great saving of time.
Problem 5. Convert 5
6
132
°
into a C jb form correct to four
significant figures.
Figure 23.4 indicates that the polar complex number 5
6
132
°
lies in the
third quadrant of the Argand diagram.
Using trigonometrical ratios,
x D 5cos 48
°
D 3.346 and y D 5 sin 48
°
D 3.716
Hence 5
66
−132
°
= −3.346 − j3.716
Alternatively, 5
6
132
°
D 5cos 132
°
C j sin132
°
D 5cos132
°
C j5 sin132
°
= −3.346 − j3.716, as above.
Figure 23.4
With this latter method the real and imaginary parts are obtained directly,
using a calculator.
Problem 6. Two impedances in an electrical network are given
by Z
1
D 4.7
6
35
°
and Z
2
D 7.3
6
48
°
. Determine in polar form the
total impedance Z
T
given that Z
T
D Z
1
Z
2
/Z
1
C Z
2
Z
1
D 4.7
6
35
°
D 4.7cos35
°
C j4.7sin35
°
D 3.85 C j2.70
Z
2
D 7.3
6
48
°
D 7.3cos48
°
C j7.3sin48
°
D 4.88 j5.42
Z
1
C Z
2
D 3.85 C j2.70 C 4.88 j5.42 D 8.73 j2.72
D
8.73
2
C 2.72
2
6
arctan
2.72
8.73
D 9.14
6
17.31
°
Hence Z
T
D Z
1
Z
2
/Z
1
C Z
2
D
4.7
6
35
°
ð 7.3
6
48
°
9.14
6
17.31
°
D
4.7 ð 7.3
9.14
6
[35
°
48
°
17.31
°
]
D 3.75
66
4.31
°
or 3.75
66
4
°
19
Revision of complex numbers 423
Further problems on the polar form of complex numbers may be found in
Section 23.7, problems 17 to 31, page 426.
23.6 De Moivre’s
theorem—powers and
roots of complex numbers
De Moivre’s theorem, states:
[r
6
q]
n
D r
n
6
nq
This result is true for all positive, negative or fractional values of n.
De Moivre’s theorem is thus useful in determining powers and roots of
complex numbers. For example,
[2
6
15
°
]
6
=2
6
6
6 ð 15
°
D 64
66
90
°
= 0 Y j64
A square root of a complex number is determined as follows:
p
[r
6
] D [r
6
]
1/2
D r
1/2
6
1
2
However, it is important to realize that a real number has two square
roots, equal in size but opposite in sign. On an Argand diagram the roots
are 180
°
apart (see problem 8 following).
Problem 7. Determine 2 C j3
5
in polar and in cartesian form.
Z D2 C j3 is situated in the second quadrant of the Argand diagram.
Thus r D
[2
2
C 3
2
] D
p
13 and ˛ D arctan 3/2 D 56.31
°
Hence the argument D 180
°
56.31
°
D 123.69
°
Thus 2 C j3 in polar form is
p
13
6
123.69
°
2 C j3
5
D [
p
13
6
123.69
°
]
5
D
p
13
5
6
5 ð 123.69
°
from De Moivre’s theorem
D 13
5/2
6
618.45
°
D 13
5/2
6
258.45
°
(since 618.45
°
618.45
°
360
°
D 13
5/2
6
101.55
°
D 609.3
66
−101
°
33
In cartesian form, 609.3
6
101.55
°
D 609.3cos101.55
°
C j609.3 sin101.55
°
D
−122 − j597
Problem 8. Determine the two square roots of the complex
number 12 C j5 in cartesian and polar form, correct to three
significant figures. Show the roots on an Argand diagram.
424 Electrical Circuit Theory and Technology
In polar form 12 Cj5 D
12
2
C 5
2
6
arctan5/12, since 12 Cj5isin
the first quadrant of the Argand diagram, i.e. 12 C j5 D 13
6
22.62
°
Since we are finding the square roots of 13
6
22.62
°
there will be two
solutions. To obtain the second solution it is helpful to express 13
6
22.62
°
also as 13
6
360
°
C 22.62
°
,i.e.13
6
382.62
°
(we have merely rotated one
revolution to obtain this result). The reason for doing this is that when
we divide the angles by 2 we still obtain angles less than 360
°
, as shown
below.
Hence
p
12 C j5 D
p
[13
6
22.62
°
]or
p
[13
6
382.62
°
]
D [13
6
22.62
°
]
1/2
or [13
6
382.62
°
]
1/2
D 13
1/2
6
1
2
ð 22.62
°
or 13
1/2
6
1
2
ð 382.62
°
from De Moivre’s theorem,
D
p
13
6
11.31
°
or
p
13
6
191.31
°
D 3.61
6
11.31
°
or 3.61
6
168.69
°
i.e., 3.61
66
11
°
19
or 3.61
66
−168
°
41
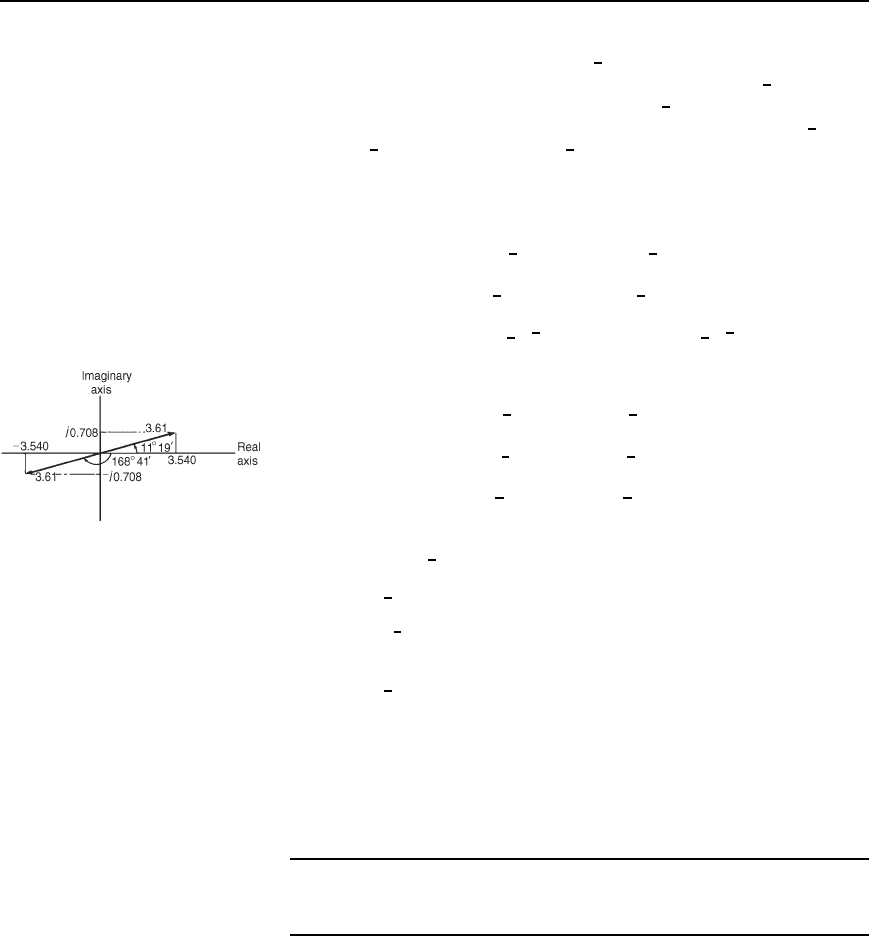
Figure 23.5
These two solutions of
p
12 C j5 are shown in the Argand diagram of
Figure 23.5. 3.61
6
11
°
19
0
is in the first quadrant of the Argand diagram.
Thus 3.61
6
11
°
19
0
D 3.61cos 11
°
19
0
C j sin11
°
19
0
D 3.540 C j0.708
3.61
6
168
°
41
0
is in the third quadrant of the Argand diagram.
Thus 3.61
6
168
°
41
0
D 3.61[cos168
°
41
0
C j sin168
°
41
0
]
D3.540 j0.708
Thus in cartesian form the two roots are
±.3.540 Y j0.708/
From the Argand diagram the roots are seen to be 180
°
apart, i.e. they
lie on a straight line. This is always true when finding square roots of
complex numbers.
Further problems on powers and roots of complex numbers may be found
in Section 23.7 following, problems 32 to 39, page 428.
23.7 Further problems
on complex numbers
Operations on Cartesian complex numbers
In problems 1 to 5, evaluate in a C jb form assuming that
Z
1
D 2 C j3,Z
2
D 3 j4,Z
3
D1 Cj2andZ
4
D2 j5
1 (a) Z
1
Z
2
(b) Z
2
C Z
3
Z
4
[(a) 1 C j7 (b) 4 C j3]
2 (a) Z
1
Z
2
(b) Z
3
Z
4
[(a) 18 C j (b) 12 Cj]
Revision of complex numbers 425
3 (a) Z
1
Z
3
Z
4
(b) Z
2
Z
3
C Z
4
[(a) 21 C j38 (b) 3 C j5]
4 (a)
Z
1
Z
2
(b)
Z
1
C Z
2
Z
3
C Z
4
(a)
6
25
C j
17
25
(b)
2
3
C j
5 (a)
Z
1
Z
2
Z
1
C Z
2
(b) Z
1
C
Z
2
Z
3
C Z
4
(a)
89
26
C j
23
26
(b)
11
5
j
12
5
6 Evaluate
1 C j
2
1 j
2
j
[4]
7IfZ
1
D 4 j3andZ
2
D 2 C j evaluate x and y given
x C jy D
1
Z
1
Z
2
C
1
Z
1
Z
2
[x D 0.188,y D 0.216]
8 Evaluate (a) 1 C j
4
(b)
2 j
2 C j
(c)
1
2 C j3
(a) 4(b)
3
5
j
4
5
(c)
2
13
j
3
13
9IfZ D
1 C j3
1 j2
evaluate Z
2
in a C jb form. [0 j2]
10 In an electrical circuit the equivalent impedance Z is given by
Z D Z
1
C
Z
2
Z
3
Z
2
C Z
3
Determine Z is rectangular form, correct to two decimal places, when
Z
1
D 5.91 C j3.15, Z
2
D 5 C j12 and Z
3
D 8 j15
[Z D 21.62 C j8.39]
11 Given Z
1
D 5 j9andZ
2
D 7 C j2, determine in a C jb form,
correct to four decimal places
(a)
1
Z
1
(b)
1
Z
2
(c)
1
Z
1
C
1
Z
2
(d)
1
1/Z
1
C 1/Z
2
[(a) 0.0472 C j0.0849 (b) 0.1321 j0.0377
(c) 0.1793 C j0.0472 (d) 5.2158 j1.3731]
Complex equations
In problems 12 to 15 solve the given complex equations:
12 4a C jb D 7 j3
a D
7
4
,bD
3
4
13 3 C j42 j3 D x C jy [x D 18,y D1]

426 Electrical Circuit Theory and Technology
14 a j3b C b j2a D 4 C j6[a D 18,bD14]
15 5 Cj2 D
p
e C jf [e D 21,fD 20]
16 An equation derived from an a.c. bridge circuit is given by
R
3
j
ωC
1
D
R
x
j
ωC
x
R
4
j/ωC
4
R
4
j/ωC
4
Components R
3
,R
4
,C
1
and C
4
have known values. Determine
expressions for R
x
and C
x
in terms of the known components.
R
x
D
R
3
C
4
C
1
,C
x
D
C
1
R
4
R
3
Polar form of complex numbers
In problems 17 and 18 determine the modulus and the argument of each
of the complex numbers given.
17 (a) 3 C j4 (b) 2 j5 [(a) 5, 53
°
8
0
(b) 5.385, 68
°
12
0
]
18 (a) 4 C j (b) 5 j3 [(a) 4.123, 165
°
58
0
(b) 5.831, 149
°
2
0
]
In problems 19 and 20 express the given cartesian complex numbers in
polar form, leaving answers in surd form.
19 (a) 6 C j5 (b) 3 j2 (c) 3
[(a)
p
61
6
39
°
48
0
(b)
p
13
6
33
°
41
0
(c) 3
6
180
°
or 3
6
]
20 (a) 5 C j (b) 4 j3 (c) j2
[(a)
p
26
6
168
°
41
0
(b) 5
6
143
°
8
0
(c) 2
6
90
°
or 2
6
/2]
In problems 21 to 23 convert the given polar complex numbers into
(a C jb) form, giving answers correct to four significant figures.
21 (a) 6
6
30
°
(b) 4
6
60
°
(c) 3
6
45
°
[(a) 5.196 C j3.000 (b) 2.000 C j3.464 (c) 2.121 C j2.121]
22 (a) 2
6
/2 (b) 3
6
(c) 5
6
5/6
[(a) 0 C j2.000 (b) 3.000 C j0 (c) 4.330 Cj2.500]
23 (a) 8
6
150
°
(b) 4.2
6
120
°
(c) 3.6
6
25
°
[(a) 6.928 C j4.000 (b) 2.100 j3.637
(c) 3.263 j1.521]
In problems 24 to 26, evaluate in polar form.
24 (a) 2
6
40
°
ð 5
6
20
°
(b) 2.6
6
72
°
ð 4.3
6
45
°
[(a) 10
6
60
°
(b) 11.18
6
117
°
]

Revision of complex numbers 427
25 (a) 5.8
6
35
°
ł 2
6
10
°
(b) 4
6
30
°
ð 3
6
70
°
ł 2
6
15
°
[(a) 2.9
6
45
°
(b) 6
6
115
°
]
26 (a)
4.1
6
20
°
ð 3.2
6
62
°
1.2
6
150
°
(b) 6
6
25
°
C 3
6
36
°
4
6
72
°
[(a) 10.93
6
168
°
(b) 7.289
6
24
°
35
0
]
27 Solve the complex equations, giving answers correct to four signifi-
cant figures.
(a)
12
6
/2 ð 3
6
3/4
2
6
/3
D x Cjy
(b) 15
6
/3 C 12
6
/2 6
6
/3 D r
6
[(a) x D 4.659, y D17.392 (b) r D 30.52, D 81
°
31
0
]
28 The total impedance Z
T
of an electrical circuit is given by
Z
T
D
Z
1
ð Z
2
Z
1
C Z
2
C Z
3
Determine Z
T
in polar form correct to three significant figures when
Z
1
D 3.2
6
56
°
,Z
2
D 7.4
6
25
°
and Z
3
D 6.3
6
62
°
[6.61
6
37.24
°
]
29 A star-connected impedance Z
1
is given by
Z
1
D
Z
A
Z
B
Z
A
C Z
B
C Z
C
Evaluate Z
1
, in both cartesian and polar form, given
Z
A
D 20 C j0, Z
B
D 0 j20 and Z
C
D 10 C j10
[4 j12 or 12.65
6
71.57
°
]
30 The current I flowing in an impedance is given by
I D
8
6
60
°
10
6
0
°
8
6
60
°
C 5
6
30
°
A
Determine the value of current in polar form, correct to two decimal
places. [6.36
6
11.46
°
A]
31 A delta-connected impedance Z
A
is given by
Z
A
D
Z
1
Z
2
C Z
2
Z
3
C Z
3
Z
1
Z
2
Determine Z
A
, in both cartesian and polar form, given
Z
1
D 10 C j0, Z
2
D 0 j10 and Z
3
D 10 C j10
[10 C j20, 22.36
6
63.43
°
]
