Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.


580 G. Blatter and V.B. Geshkenbein
to the disorder potential arises from fluctuations in
the pinning landscape and hence involves the square
of the pinning potential,
E
2
pin
(L) =
dz dz
pin
(0, z)
pin
(0, z
)
∼ K(0) L
2
L . (12.321)
The sublinear growth of the pinning energy
E
2
pin
(L)
1/2
has its originin the competitionbetween
the individual pinning centers: Modifying (12.286) to
describe the pinning of an individual vortex line the
fluctuationsin the pinning energy E
2
pin
(L)
1/2
can be
written as (note that only defects within a distance
away from the vortex core contribute to the pinning
energy, hence V ∼
2
L, and we can drop the factor
(/a
0
)
2
)
E
2
pin
(L)
1/2
≈ (f
2
imp
n
imp
2
L)
1/2
,
≈ f
2
imp
n
imp
2
. (12.322)
The last equation relates the disorder parameter
to the individual pinning force f
imp
and the impu-
rity density n
imp
; the disorder parameter then can
be determined via the defect induced variation in the
Ginzburg–Landau parameters ˛ and m followingthe
above scheme [150] or via a direct calculation of the
individual pinning force f
imp
[362,363].
Following the general ideas of weak collective pin-
ning theory (cf. Sect. 12.8.2) we have to cut the sub-
linear growth of (12.321) on the collective pinning
length L
c
. The latter is found by minimizing the free
energy of the vortex with respect to the length L over
which the pinning forces add up randomly and we
will do this via scaling estimates (in such estimates
we will drop all numerical factors and we will remind
the reader by the use of the symbol “∼”; a more ac-
curate scheme providing estimates forthese numeri-
cal prefactors is the dynamical approach introduced
by Schmid and Hauger and by Larkin and Ovchin-
nikov [8,9]).We start from the freeenergy (12.313) of
a vortex line subject to a disorder potential
pin
and
estimate the energy involved in displacing a vortex
segment of length L by u ≤ r
pin
.Whilethedisorder
potential contributes an energy gain −
2
L(u/),
cf. (12.321),the elastic distortion of the line costs an
energy "
l
u
2
/L. Minimizing the free energy density
f ∼
"
l
2
u
2
L
2
−
7
2
L
u
(12.323)
for the maximal displacement u ∼ r
pin
≈ we ob-
tain the collective pinning length L
c
and the pinning
energy U
c
,
L
c
∼
"
2
l
2
/
1/3
, (12.324)
U
c
∼
2
L
c
1/2
∼
"
l
4
1/3
∼ H
2
c
4
/L
c
.
Each segment of length L
c
of the vortex then is
pinned by the collective action of all the defects
within the collective pinning volume V
c
∼
2
L
c
,
which then act to produce a finite pinning potential
U
c
. Within each pinning valley u < the displace-
ment u grows with distance following a 3/2-power
law, cf. (12.317)
u ∼ (L/L
c
)
3/2
. (12.325)
Finally, using the characteristic transverse scale
r
pin
≈ of the pinning landscape
pin
,weobtain
a pinning force f
pin
∼ ( L
c
)
1/2
. The critical cur-
rent density j
c
follows from comparing f
pin
with the
Lorentz force j
c
¥
0
L
c
/c and we obtain
j
c
∼
c
¥
0
L
c
1/2
∼ j
0
L
c
2
, (12.326)
with the depairing current density j
0
≈ "
0
c/¥
0
in-
troduced above, see (12.7).
The regime of weak collective pinning is char-
acterized by a large suppression of the critical cur-
rent density j
c
with respect to the depairing value j
0
and hence the collective pinning length L
c
should be
much larger than thecoherence length ,L
c
.The
latter conditionis consistentwith our useof elasticity
theory in the determination of the collective pinning
length. On the other hand,for L
c
<
the distortion of
the vortexlineis large,elasticitytheory breaks down,
and the pinning is strong.
Experimentally, the collective pinning length L
c
is
difficult to determine, one possibility being to inves-
tigate the thickness dependence of the critical cur-
rent density in a thin film [364–366]. On the other
hand, the collective pinning energy U
c
can be deter-
mined more directly in a magnetic relaxation exper-
iment by measuring the creep rate, see Sect. 12.9.4.
12 Vortex Matter 581
The quantity most easily amenable to experimental
measurement is the critical current density j
c
.
A comparison of the critical current density j
c
withexperimentalresultsprovidesuswithacheck
for the validity of collective pinning theory.We then
are forced to study the microscopic origin of the dis-
order and determine the parameter .Alternatively,
we can take a more phenomenological point of view
and regard j
c
as the simplest experimentally accessi-
ble quantity which we can use for the characteriza-
tion of the disorder potential.Taking the latter point
of view we express the collective pinning length L
c
and the collective pinning energy U
c
by the critical
current density j
c
,
L
c
∼
j
0
j
c
1/2
, U
c
∼ H
2
c
3
j
c
j
0
1/2
. (12.327)
The results (12.325) and(12.326) apply to the limit
of an isolated vortex, i.e., for weak enough mag-
netic fields such that we can neglect the interac-
tion between neighboringvortices.Comparingshear
(c
66
(u/a
0
)
2
La
2
0
∼ "
0
(u/a
0
)
2
L)andtilt("
l
u
2
/L)ener-
gies produced in a deformation u on scale L we find
that we can neglect the interaction with other vor-
tices if a
2
0
> ("
0
/"
l
)L
2
. Inserting the collective pin-
ning length L ∼ L
c
we find that the single vortex
pinning regime extends up to magnetic fields of or-
der
B
sv
∼
j
c
j
0
H
c
2
. (12.328)
Anisotropic Material
In generalizing the above results to the situation in
anisotropic materials we can follow the conventional
routeand rederive the various expressions while tak-
ing the material anisotropy into account [206]. How-
ever, since pinning involves the length scale it
is more convenient to use the scaling approach (see
Sect.12.6) and generalize all isotropic results directly
to the anisotropic case.
For isotropic superconductors we have found a
collective pinning length L
c
∼ ("
2
0
2
/ )
1/3
,apin-
ning energy U
c
∼ (
2
L
c
)
1/2
, a critical current den-
sity j
c
∼ j
0
(/L
c
)
2
, and the limiting field B
sv
≈
(j
c
/j
0
)H
c
2
.Using our scaling rule (12.170) we proceed
with the following arguments: The collective pinning
length L
c
is a longitudinal length, therefore L
c
(# )=
("/"
#
)
˜
L
c
.In order to obtain
˜
L
c
∼ ( ˜"
2
0
˜
2
/ ˜ )
1/3
we have
to express all rescaled material parameters (
˜
,
˜
, ˜ )
by the original parameters (
˜
= ,
˜
= , ˜ = /"),
hence
˜
L
c
∼ ("
2
0
2
"/ )
1/3
and we obtain the final re-
sult
L
c
(# )=
L
c
c
"
#
, L
c
c
= "
4/3
L
iso
c
∼
"
2
2
"
4
1/3
.
(12.329)
Here, L
c
c
is the collective pinning length for the case
where the magnetic field is aligned with the c-axis
and L
iso
c
denotes the collective pinning length in an
equivalent isotropic material (" = 1) with identical
material parameters , ,and . The pinning po-
tential U
c
is a scalar quantity; after rescaling, the
isotropized system does not emphasize a particu-
lar direction and hence the pinning potential should
not depend on the angle # . The scaling factor for U
c
is s
E
= " and rewriting
˜
U
c
in terms of the original
material parameters we obtain the result
U
c
c
= "
2/3
U
iso
c
∼ "
2/3
"
0
4
1/3
, (12.330)
independent of the angle # , as expected. In the
anisotropic material we have to distinguish between
two critical current densities, the in-plane critical
current density j
c
x involving a Lorentz force along
y
,andj
⊥
c
y
, the out-of-plane critical current den-
sity,pushingthe vortices along the direction of the x-
axis.The in-plane critical current density is obtained
from rescaling the force balance equation between
the pinning and the Lorentz force,
˜
j
c
¥
0
˜
L
c
∼
˜
U
c
.The
in-plane critical current density then scales like a
planar length and thus j
c
=
˜
j
c
= "
−2/3
j
iso
c
= j
c
c
.On
the other hand, for the out-of-plane critical current
density we have to orthogonalize the Lorentz force
after rescaling (cf. (12.174) and (12.175)) such that
j
⊥
c
scales like a transverse length, therefore j
⊥
c
= "
#
˜
j
c
and we obtain the result j
⊥
c
(# )="
#
j
c
c
; in summary,
j
c
= "
−2/3
j
iso
c
= j
c
c
, j
⊥
c
(# )="
#
j
c
c
. (12.331)
Finally, the field B
sv
limitingtheregimeofsin-
gle vortex collective pinning becomes B
sv
(# ) ∼
(j
c
c
/j
0
)H
c
2
(# ),wherewehaveusedthescalingrulefor
582 G. Blatter and V.B. Geshkenbein
magnetic fields and the above result for the transfor-
mation of the in-plane critical current density j
c
.
12.9.3 Vortex L attice Pinning
When studying the weak collective pinning of a bulk
vortexlatticewehavetoaccountforbothshearand
tilt deformations; the additional shear energy takes
care of the interaction energy produced in the relax-
ation to the disorder landscape (the large compres-
sionmodulusinhibitsdensitymodulationsandwe
canignorethistermintheelasticenergy).Incom-
paring the tilt and shear energies of a lattice defor-
mation u we have to account for the dispersion of the
tilt modulus c
44
, see (12.74),
E
tilt
V
∼ c
44
u
2
L
2
∼
B
2
/4
1+
2
/R
2
u
2
L
2
,
E
shear
V
∼ c
66
u
2
R
2
∼
¥
0
B
(8)
2
u
2
R
2
. (12.332)
Here, R and L are the transverse (perpendicular to
the field) and longitudinal (along the field) lengths
associated with the deformation u and V ≈ R
2
L is
the bundle volume. Comparing these tilt and shear
energies we find the geometry of the pinned vortex
bundles,
L ∼
c
44
(R)
c
66
R ∼
⎧
⎪
⎪
⎨
⎪
⎪
⎩
R
a
0
R , a
0
< R < ,
a
0
R , < R .
(12.333)
Due to the anisotropic elastic properties (soft shear
modulus) of the vortex lattice the displacement field
u(R, L) grows faster along the transverse dimension:
the surfaces of constant amplitude u
2
(R, L)
1/2
=
const. are cigar shaped with L R. Note that the
aspect ratio L/R grows rapidly within the dispersive
regime a
0
< R < .
In addition, the shear and tilt energies compete
with the pinning energy; again, only fluctuations in
the disorder landscape will lead to a finite pinning
energy and we have to determine (cf. 12.286)
E
2
pin
(V) =
d
3
r d
3
r
E
pin
(0, r)E
pin
(0, r
)∼
2
a
2
0
V .
(12.334)
Balancing the pinning energy against the elastic
(shear) energy within the volume V we obtain the
second relation between the transverse and longitu-
dinal bundle lengths
R
2
∼
c
2
66
2
a
2
0
L ∼
L
c
a
0
3
a
0
L . (12.335)
Here, we have made use of (12.325) and the expres-
sion "
l
≈ "
0
for the line elasticity in an isotropic
material (note that we use the single vortex pin-
ning length L
c
as a disorder parameter). Making
use of the relation L ∼ (/a
0
)R valid in the non-
dispersive regime we find the expressions for the
bundle dimensions R
c
and L
b
c
, the pinning energy
U
b
c
∼ c
66
(/R
c
)
2
V
c
and the critical current density
j
b
c
∼ cU
b
c
/BV
c
,
R
c
∼
L
c
a
0
3
> ,
L
b
c
∼ L
c
a
0
2
L
c
a
0
2
>
a
0
, (12.336)
U
b
c
∼ U
c
a
0
2
L
c
a
0
4
,
j
b
c
∼ j
c
a
0
2
a
0
L
c
4
, (12.337)
where we have expressed the results for the vortex
bundle through the single vortex quantities L
c
∼
("
2
0
2
/ )
1/3
, U
c
∼ "
0
2
/L
c
,andj
c
∼ j
0
U
c
/"
0
L
c
.
Comparing the pinning energy [E
2
pin
(u, V)]
1/2
∼
[( u
2
/a
2
0
)V]
1/2
within one pinning valley with the
shear energy we find the scaling of the displacement
u with distance R ,
u
2
∼
2
a
0
L
c
3
R
2
a
0
L
∼
2
a
0
L
c
3
R
. (12.338)
When attempting to repeat this scaling analysis
for the dispersive regime a
0
< R < we find
that the transverse scale R drops out of the var-
ious relations (cf. equations (12.333) and (12.335),
(12.338)), hence one may suspect that the displace-
ment u grows only logarithmically with distance R,
a behavior that cannot be obtained within a simple
scaling approach. We then have to change our strat-
egy and determine the mean squared displacement
12 Vortex Matter 583
field u
2
(R, L)≡[u(R, L)−u(0, 0)]
2
with the help
of perturbation theory using the small disorder pa-
rameter [10]; the relation u
2
(R
c
, L
c
)≈
2
then
directly determines the bundle geometry in terms
of the disorder parameter and the results for the
pinning energy and the critical current density are
trivially obtained via scaling.
We start from the static (! =0)versionofthe
force equation (12.90) with the force F
pin,ˇ
(u, r) ≡
−@
u
ˇ
E
pin
(u, r) deriving from the disorder landscape,
u
˛
(k)=G
˛ˇ
(k, ! =0)F
pin,ˇ
(u, k) . (12.339)
To lowest order we can set u =0ontherighthand
side of (12.339) and determine the correlator
u
2
(k) =
d
3
k d
3
k
(2)
6
G
˛ˇ
(k)G
˛ˇ
(k
)
×F
pin,ˇ
(0, k)F
pin,ˇ
(0, k
) ,
(12.340)
with the force correlator deriving from the energy
correlator (12.312), in Fourier space,
F
pin,ˇ
(0, k)F
pin,ˇ
(0, k
) =−(2)
3
a
2
0
ı
ˇˇ
ı(k + k
) .
(12.341)
Combining (12.340) and (12.341) we obtain the real
space mean squared correlator
u
2
(r) =
2
a
2
0
d
3
k
(2)
3
[1 − cos(k · r)]
× G
˛ˇ
(k)G
˛ˇ
(−k) . (12.342)
The main term in (12.342)originatesfrom the trans-
verse part in G
˛ˇ
and the largest contribution to the
integral
u
2
(r) =
2
a
2
0
d
3
k
(2)
3
[1 − cos(k · r)]
[c
66
K
2
+ c
44
(k)k
2
z
]
2
(12.343)
derives from long wavelengths k → 0. The
evaluation is done separately for the dispersive
(c
44
≈ 4"
0
/a
4
0
K
2
)andthenon-dispersive(c
44
≈
4"
0
2
/a
4
0
) regimes describing the situation at small
(a
0
< R < ) and large (R > ) distances [150] and
interpolating between the two results we find (under
the conditions that u
2
≤
2
and a
0
< L
c
)
u
2
(R, L)∼
2
a
0
L
c
3
R
2
2
+
a
2
0
L
2
4
1/2
+ln
1+
R
2
a
2
0
+
L
a
0
.
(12.344)
Whilethefirstterm in(12.344) reproducestheresults
(12.333) and (12.338) found previously in the non-
dispersive regime, the second term dominates in the
dispersive region on small scales R < and provides
us with the new result u
2
(R)∼
2
(a
0
/L
c
)
3
ln(R/a
0
)
— indeed the mean squared displacement grows
only logarithmically in the intermediate regime a
0
<
R < .
The condition u
2
(R)∼
2
provides us with an
expression for the pinning length R
c
R
c
∼ a
0
exp
c
L
c
a
0
3
; (12.345)
theconstant c in the exponent depends on the numer-
ical ˛ chosen in the pinning criterion u
2
(R)≈˛
2
and cannot be obtained within the present perturba-
tive analysis.The remainingcharacteristic quantities
are obtained with the help of scaling estimates and
we arrive at the following results valid in the disper-
sive region,
R
c
∼ a
0
exp
c
L
c
a
0
3
< ,
L
b
c
∼ a
0
exp
2c
L
c
a
0
3
<
a
0
(12.346)
U
b
c
∼ U
c
L
c
a
0
exp
2c
L
c
a
0
3
,
j
b
c
∼ j
c
L
c
a
0
2
exp
−2c
L
c
a
0
3
. (12.347)
Lacking a numerical value for the constant c in the
exponent heavily reduces the degree of accuracy of
these scaling results as compared to the results ob-
tained for the single vortex pinning regime and the
vortex bundle pinning regime in the non-dispersive
case — while the latter are accurate up to a numer-
ical prefactor, the indeterminacy of c lifts our igno-
rance to the exponent. This situation can be greatly

584 G. Blatter and V.B. Geshkenbein
improved with the help of the functional renormal-
ization group theory [357], cf. (12.320): the disper-
sion in the elastic modulus c
44
(k)renderstheprob-
lem effectively four-dimensional (where the disor-
der is marginally relevant) and the divergence in the
fourth derivative K
IV
l→l
c
(0) →∞of the disorder cor-
relator at the origin allows for a precise definition of
the Larkin length R
c
∝ exp(l
c
). The crucial quan-
tity relating the disorder potential to the pinning
force then is the fourth derivative K
IV
(0) of the dis-
order correlator at the origin — this differs from
the perturbative analysis [cf. (12.316)] where this
role is played by the combination K
(0)/
2
involving
the second derivative K
(0) (due to the force–force
correlator describing the disorder potential in one
pinning valley) and the disorder scale (from the
condition u
2
(R
c
)≈
2
); within a scaling analysis,
K
IV
(0) ∼ K
(0)/
2
∼ K(0)/
4
.
Integrating the RG flow through theLarkin regime
0 < l ≤ l
c
andidentifying thedivergence of K
IV
l
(0) at
l = l
c
the one-loop analysis provides the result [347]
R
c
∼ a
0
exp
4
3/2
3
"
2
0
a
3
0
K
IV
(0)
. (12.348)
A similar analysis [367] for the single vortex pinning
provides the result L
c
∼ ["
2
0
/K
IV
(0)]
1/3
but fails to
provide an accurate numerical for the prefactor. It
is then quite appropriate to redefine L
c
as given by
(12.325) to read L
c
≡ ["
2
0
/K
IV
(0)]
1/3
; this allows us
to cast the result (12.348) into the form (12.345)with
c =4
3/2
/3,
R
c
∼ a
0
L
c
a
0
7−5ln(4/3)
9
exp
4
3/2
3
L
c
a
0
3
. (12.349)
The remaining formulae then follow from scaling.
The prefactor ∼ (L
c
/a
0
)
0.62
in (12.349) can be ob-
tained within a two-loop analysis of the RG flow
[346,347]; the result (12.349) then provides us with
an expression for R
c
up to an unknown overall nu-
mericalprefactor andthusputs the dispersive regime
on the same level of accuracy as the single vortex and
large bundle pinning regimes.
The dispersive regime with its “small” bundles of
size a
0
< R
c
< is limited to the intermediate field
region
B
sv
< B < B
sb
∼
j
c
j
0
ln
2
j
c
j
0
2/3
H
c
2
; (12.350)
the field B
sb
marking the onset of the non-dispersive
regime with its characteristic “large” bundles differs
from B
sv
only by a logarithmic factor. The explicit
field dependence of the results (12.346) and (12.347)
follows from the substitution
L
c
a
0
∼
j
0
j
c
B
H
c
2
1/2
. (12.351)
Anisotropic Material
The discussion of pinning in anisotropic materials is
quite involved and we restrict the analysis to the case
of uniaxially anisotropic superconductors with the
magnetic field applied along the high symmetry di-
rection. We proceed along the traditional path using
scaling estimates and calculate the bundle size, the
pinning energy U
b
c
and the critical current density
j
b
c
. Repeating the derivation of (12.353) above with
the appropriate expression (12.83) for the tilt modu-
lus we obtain the displacement correlator
u
2
(R, L)∼
2
a
0
"
L
c
c
3
"
R
2
2
+
a
2
0
L
2
4
1/2
(12.352)
+ln
1+
R
2
a
2
0
+
L
"a
0
.
ThebundlesizeR
c
then follows from the definition
u
2
(R
c
)∼
2
,
R
c
∼
⎧
⎪
⎪
⎨
⎪
⎪
⎩
a
0
exp
c
L
c
c
"a
0
3
, a
0
< R
c
< /" ,
"
L
c
c
"a
0
3
, /" < R
c
,
(12.353)
and the corresponding expressions for L
b
c
followtriv-
ially. Replacing L
c
/a
0
→ L
c
c
/"a
0
and → /" in
(12.337) and (12.347) we obtain the pinning energy
U
b
c
and the planar critical current density j
b
c
in the
anisotropic situation. The boundary B
sb
limiting the
small bundle pinning regime takes the form
B
sb
∼
j
c
c
j
0
ln
2
"
2
j
c
c
j
0
2/3
H
c
2
. (12.354)
12 Vortex Matter 585
12.9.4 Collective Creep
In the absence of thermal (and quantum) fluctua-
tions the vortex system remains firmly pinned for
driving forces f below critical, f < f
c
; the depinning
at f
c
then is an example of a dynamical phase tran-
sition [368, 369]. Thermal or quantum fluctuations
allow the vortices to overcome the pinning barriers
at small applied forces f < f
c
, either via thermal ac-
tivation or quantum tunneling; the resulting vortex
motion (cf. 12.8.4) smears the transition at f
c
and
reintroduces dissipation. However, within the collec-
tive pinning scheme the barriers inhibiting vortex
motion diverge as the driving force f is decreased,
resulting in a“glassy”andhence“truly superconduct-
ing” response as f → 0. In the following, we analyze
this collective creep type motion, concentrating first
on thermal processes; we discuss the motion of indi-
vidual vortex lines and proceed with classical creep
of vortex bundles. Second, we extend the analysis to
quantum motion of vortices.
Single Vortex Creep
The classical creep-type motion of an individual
vortex line can be visualized as a thermal diffu-
sion process where vortex segments move between
metastable states. In the absence of an external cur-
rent density j a vortex segment lowers its energy by
finding the optimal low energy state. With an ap-
plied current density j a new metastable state be-
comes more favorable and the vortex moves. The
new optimal states are determined by the condition
that the energy gain due to the driving Lorentz force
matches the energy of the newly deformed vortex
configuration. Fora current density j near criticality
this condition is already fulfilled forthe neighboring
metastable state a distance ∼ away. However, upon
decreasing the current density j the Lorentz force is
reduced and the next favorable metastable state is
further away. As a consequence, the thermal motion
of the vortex will involve more extended segments
hopping larger distances in order to reach the next
optimal low energy state, see Fig. 12.26.
For a quantitative analysis we need to know more
about the low lying metastable states of the vortex in
its random pinning environment. This touches upon
the general problem of elastic manifolds in quenched
random media, of which our vortex line is a typ-
ical example [111, 112, 370], see Sect. 12.9.1. Con-
sider a d = 1-dimensional elastic string moving in n
transverse directions as described by the free energy
(12.313). The statistical mechanics of this object is
given by the partition function
Z =
(u,L)
(0,0)
D[u
]exp
−
1
T
L
0
dz
(12.355)
×
"
l
2
@u
@z
2
+
pin
(u
, z
)
.
Disorder is always relevant for dimensions n ≤ 2and
the string is in a pinned phase characterized by a
displacement correlator with a wandering exponent
n
> 1/2 (an exponent 1/2 corresponds to thermal
wandering, "
l
u
2
/L ∼ T)
u
2
(L)≡[u(L)−u(0)]
2
∼
2
L
L
c
2
n
. (12.356)
For L < L
c
(Larkin regime) the string probes only a
single pinning valley; the wandering exponent
L
1
=
3/2 has been derived above using scaling arguments,
see (12.325) and (12.317). The crossover length L
c
limiting this regime also has been calculated above,
L
c
≈ ["
2
l
2
/ ]
1/3
. At larger distances L > L
c
the
string can choose between many metastable minima
[350,351].Thedetermination of thewandering expo-
nent
1,n
is a nontrivial problem (cf. the discussion
in Sect. 12.9.1); its numerical value depends on the
dimensionality of the transverse space:
1,1
=2/3is
an exact result [356], while for n =2numericalsim-
ulations [371,372] give a value
1,2
≈ 0.620 ≈ 5/8.
Metastable states extending over a distance L are
separated by a typical distance u(L) ∼ (L/L
c
)
1,n
and different minima vary in depth by an amount
ı
pin
(L) ∼ U
c
(L/L
c
)
1,n
; the exponent
1,n
=2
1,n
−1
follows from scaling, assuming that variations in the
pinning energy ı
pin
(L) scale as the elastic energy
"
l
u
2
/L ∝ L
2
1,n
−1
.
The situation is different for dimensions n > 2
[373], where a finite “roughening” temperature sep-
arates a low temperature disorder dominated phase
from the high temperature thermal phase character-
ized by
th
1
=1/2.The (1+2)-problem corresponds to
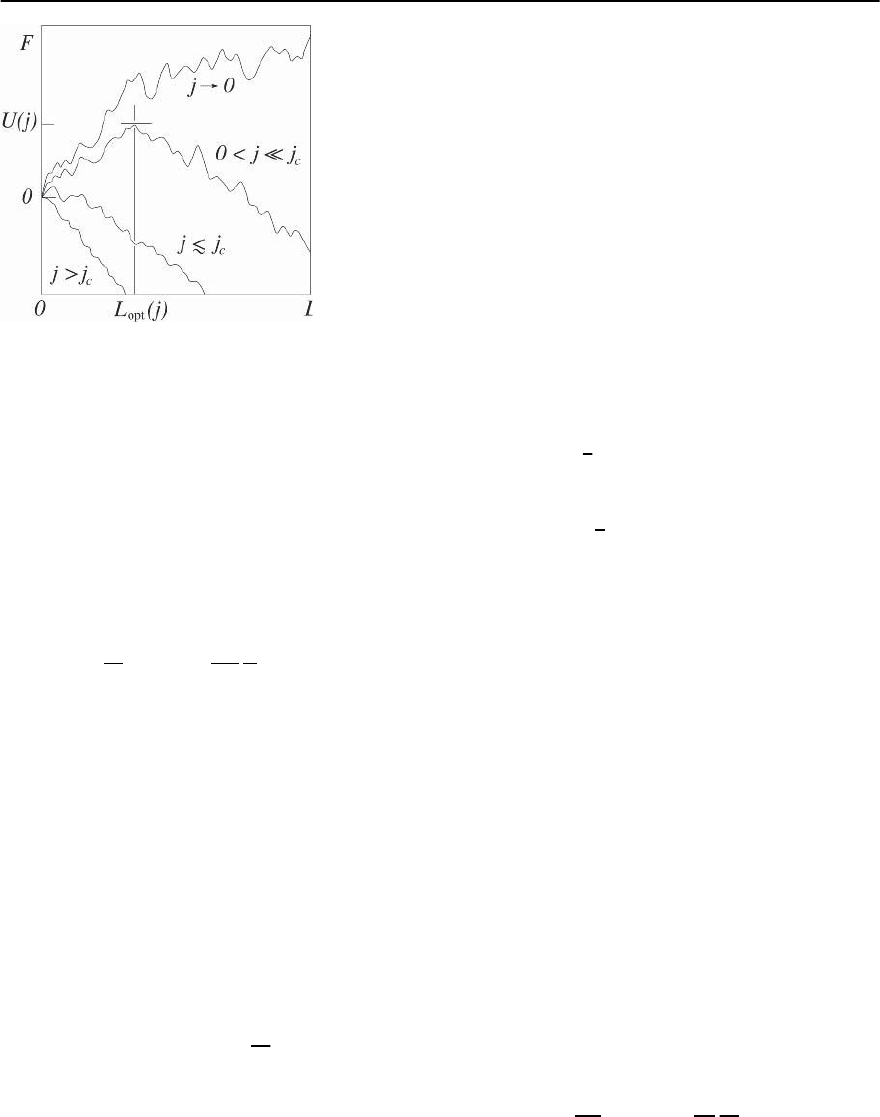
586 G. Blatter and V.B. Geshkenbein
Fig. 12.26. Effective tilted random potential acting on the flux line in the presence of quenched disorder and with an
applied driving current j. The vortex line relaxes into a low energy metastable state. Close to the critical driving force,
j ≤ j
c
, the next metastable state is near to the original state and separated from the latter only by a small barrier
U(j) ∼ U
c
(1 − j/j
c
). At low driving currents j j
c
the closest favorable metastable state is far away from the original
one and separated from the latter by a large barrier, U(j ) ∼ U
c
(j
c
/j)
. Hops to the closest valleys are not favorable and
represent only an intermediate step in the diffusive motion of the vortex to its next optimal state
the lower criticaldimension for this phase transition
and thus exhibits marginal behavior,see Sect. 12.9.5
below. However, for the physically relevant case dis-
cussed here, n = 2 and a single vortex is always in a
pinned or “glassy” state.
Letus return to our original problem and apply the
above results to the discussion of vortex creep. The
free energy of a vortex segment of length L trapped
in the disorder potential and driven by a small cur-
rent density j j
c
takes the form (see Fig. 12.27;
below, we drop the indices “1, n” on the wandering
exponent )
F(L) ∼ U
c
L
L
c
2−1
− j
¥
0
c
L
c
L
L
c
1+
, (12.357)
where we have assumed that the barriers inhibiting
vortex motion scale the same way as the metastable
minima [374].Equation (12.357) reduces the present
discussion to a simple nucleation problem [375]
where the vortex segment plays the role of the nucle-
ation bubble: whereas nuclei with lengths L smaller
than some critical length L
opt
will collapse back to
zero length and thus are undercritical, activated seg-
ments with a length L > L
opt
will expand and con-
tribute to the vortex motion (see [376] for a simi-
laranalysisofdomainwallmotioninspinglasses
and [377] for a description of dislocation motion in
metals). The critical size of the nucleus derives from
the minimal barrier in (12.357) and defines a creep
barrier which increases algebraically with decreasing
current density j,
L
opt
(j) ∼ L
c
j
c
j
1/(2−)
, U (j) ∼ U
c
j
c
j
,
(12.358)
with the exponent =(2 −1)/(2 − ). Correspond-
ingly, the current-voltage characteristic exhibits a
highly non-linear“glassy” behavior at low drive
V ∝ exp
−
U
c
T
j
c
j
. (12.359)
Using the above estimate
2
≈ 5/8 for a single vortex
in three dimensions we obtain
L
opt
(j) ∼ L
c
j
c
j
8/11
,
u(j) ∼
j
c
j
5/11
,
U(j) ∼ U
c
j
c
j
2/11
. (12.360)
A non-linear increase of the creep barrier with de-
creasing current density has been observed experi-
mentally by various groups, see [345,378–381].
12 Vortex Matter 587
Combining (12.358) and (12.302) we obtain a non-
linear logarithmic time decay of the current density,
j(t) ∼ j
c
T
U
c
ln
t
t
0
−1/
. (12.361)
For current densities near to critical the result
(12.304) is more appropriate and interpolating be-
tween these two formulae we obtain the general be-
havior
j(t) ∼ j
c
1+
T
U
c
ln
1+
t
t
0
−1/
(12.362)
valid close to j
c
as well as for j j
c
[337]. A non-
linear time logarithmic decay of the trapped diamag-
netic moment has been observed in several experi-
ments [46–48,345,380–382].
Within the single vortex pinning regime the expo-
nent 1/ ≈ 11/2 is large and rewriting the solution
(12.362) for small temperatures and small times in
exponential form,
j(t) ∼ j
c
exp
−
T
U
c
ln
t
t
0
, T ln
t
t
0
<
11
2
U
c
,
(12.363)
we find an algebraic time decay of the current and an
exponential dependence on temperature,
j(t) ≈ j
c
t
0
t
T/U
c
, j(T) ≈ j
c
exp
−
T
T
0
,
(12.364)
with T
0
≈ U
c
/ ln(t/t
0
). A sample prepared in a criti-
cal state at t = 0 will carry a strongly reduced screen-
ing current j j
c
after only a few seconds of waiting
time: The quantity measured in a magnetization ex-
periment is usually not the critical current density
j
c
but the strongly reduced value j(T). Such an ex-
ponential decrease of the apparent critical current
density has indeed been observed in the oxide su-
perconductors and the characteristic temperature T
0
has been measured to be of the order of 10 K [49].
Typical experimental values for the activation en-
ergy U
c
are of order 10
2
—10
3
K [45,46,345,383,384]
whiletypical experimental waitingtimesareof order
t/t
0
∼ 10
10
, hence T
0
is related to U
c
as expected.
Returning to the general result (12.362) we de-
termine the normalized creep rate S =−dlnj/dlnt
which differs from Anderson’s result T/U
c
due to the
nonlinear dependence of the activation barrier U(j)
on the current density j,
S ≈
T
U
c
+ T ln(1 + t/t
0
)
. (12.365)
Equation (12.365) shows two interesting features
which area direct consequence of thecollectivecreep
behavior with its characteristic strong increase of
the pinning barrier (12.305) with decreasing current
density: First,the decay rateS decreases with increas-
ing time, producing an upward curvature in a plot of
the logarithmic time decay of the diamagnetic cur-
rent [48,385]. Second, the decay rate S saturates for
temperatures T > U
c
/ ln(t/t
0
), S
sat
≈ 1/ ln(t/t
0
).
Both these effects are a consequence of the decaying
current density j due to creep and the concomitant
increase of the system barriers as time evolves [386].
However, we cannot expect this saturation to appear
within the single vortex pinning regime: Near satu-
ration the ratio T ln(t/t
0
)/U
c
in (12.362) has be-
come larger than unity and the current density has
decayed by a factor ∼ 10
−2
.Atsuchsmallcurrent
densities the interaction between neighboring vor-
tices cannot be neglected any longer and the vortex
motion proceeds by the diffusion of vortex bundles
rather than independent single vortices.As discussed
below, creep due to vortex bundles is characterized
by an exponent of order unity and a saturation S
sat
of order of a few percent is expected, in agreement
with experiment. Also, experiments show a satura-
tion at temperatures T > 10 K in agreement with a
collective pinning energy of order 10
2
Kasobtained
above.
As we have already mentioned above, the analy-
sis of collective creep in terms of individually mov-
ing vortices applies only for a limited regime of
current densities j, the reason being that the pin-
ning energy grows only sublinearly in the length L,
whereas the interaction energy between neighbor-
ing vortices grows linearly in L. Thus with decreas-
ing current density j the relative importance of the
interaction between the vortices grows. We identify
the length scale where the intervortex interaction
becomes dominant by comparing the shear energy
c
66
(u/a
0
)
2
a
2
0
L with the tilt energy "
l
(u/L)
2
L;with
c
66
= "
0
/4a
2
0
and "
l
≈ "
0
we find a (longitudinal)
588 G. Blatter and V.B. Geshkenbein
Fig. 12.27. Free energy F versus length L of the hop-
ping segment. The free energy involves the barrier energy
U
c
(L/L
c
)
2−1
growing slowly with L and the energy gain
due to the Lorentz force, (j/j
c
) U
c
(L/L
c
)
1+
,withasmall
prefactor j/j
c
1 but a more rapid growth in L.Fora
fixed driving current density j a minimal segment of length
L
opt
(j) has to overcome the barrier U (j) in order to reach
the next metastable state.With decreasing j the barrier di-
verges with U(j) ∼ U
c
(j
c
/j)
and =(2 −1)/(2 − )
crossover length L ∼ a
0
; single vortex creep thus is
limited to currents such that L
opt
(j
sv
) < a
0
and using
(12.358) we obtain
j
sv
∼ j
c
L
c
a
0
2−
∼ j
c
B
H
c
2
j
0
j
c
(2−)/2
. (12.366)
For small current densities j < j
svc
or large fields
B > B
sv
the interaction between vortices is impor-
tant and the minimal barrier for flux motion involves
a small vortex bundle instead of a single vortex line.
Weadd a note on single vortex creep in anisotropic
materials: The relevant length L
opt
(j)(sizeofthe
critical nucleus) increases with decreasing (in-
plane) current density j according to L
opt
(j, # ) ∼
L
c
(# )(j
c
c
/j)
8/11
, and similar results apply for the
thermal activation barrier (classical creep), U(j) ∼
U
c
c
(j
c
c
/j)
2/11
(note that the creep barrier is a scalar
quantity and hence one expects a result independent
of the angle # ). The boundary of the single vortex
pinning regime is reached when the current density
j drops below j
svc
(# , B) ∼ j
c
c
(
√
"
#
L
c
c
/"a
0
)
11/8
,aresult
obtained from rescaling the condition L
opt
(j, # ) ∼
a
0
. If the vortex lattice is subject to an out-of-plane
current density j y
the creep motion is directed
along the superconducting planes. For this case we
have to substitute the in-plane current density ratio
j
c
c
/j and the boundary j
sv
by their out-of-plane coun-
terparts "
#
j
c
c
/j and "
#
j
sv
.
Creep of Vortex Bundles
Creep of vortex bundles involves an additional new
feature not present in the discussion of single vor-
tex creep: the jump of the vortex bundle to the next
valley involves a finitecompression of the vortex lat-
tice. Indeed, in order to gain energy from the driving
Lorentz force the lattice has to undergo a compres-
sion: Consider a displacement u(r)restrictedtothe
bundle volume V , then the energy gain E
L
due to the
Lorentz force is given by
E
L
(V)=
1
c
dV (j ∧ B) · u (12.367)
=−
1
c
dV [(j ∧ B) · r](∇·u) .
With the compression modulus c
11
much larger than
the shear modulus c
66
the compressed vortex bun-
dle elongates along the direction of motion (we call
the resulting elongated bundle a “superbundle”). A
simple scaling analysis can be applied in the non-
dispersive regime: comparing the compression and
shear energy densities c
11
(u/R
)
2
∼ c
66
(u/R
⊥
)
2
we
find the asymmetry ratio R
/R
⊥
∼ /a
0
between
the parallel and perpendicular (to the bundle mo-
tion) dimensions of the superbundle. The superbun-
dle is made from subbundles forming independently
via the competition between the elastic tilt and shear
energies and the disorder potential, hence R
⊥
= R
c
follows from optimizing the geometry of the sub-
bundles. For the creep process, the large value of the
compression modulus c
11
c
66
prohibits the hop-
ping of individual subbundlesand thereforethelatter
are coupled together, leading to the hop of the large
superbundle.The activation energy U
b
c
forsuchacor-
related hop then is given by the sum of the activation
energies for the subbundles,
U
sb
c
∼ c
66
u
2
R
2
⊥
R
⊥
R
L
b
∼
R
R
c
L
b
L
b
c
U
c
. (12.368)
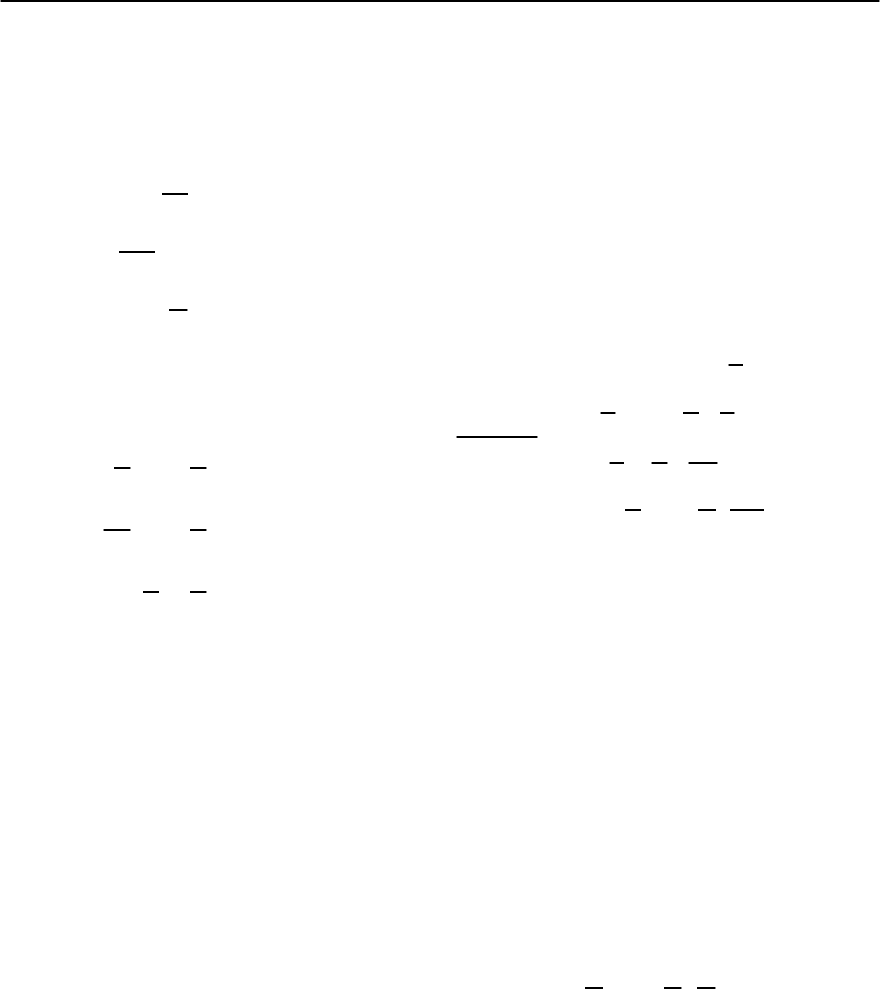
12 Vortex Matter 589
The analysis of the superbundle dimensions in
the dispersive and mixed dispersive/non-dispersive
regimes requires some care in the evaluation of the
compression, tilt, and shear energies [38, 387] and
produces the results
R
∼ L
b
∼
R
2
⊥
a
2
0
R
⊥
, R
⊥
< R
∼ L
b
< ,
R
∼ L
b
∼
R
⊥
a
2
0
1/2
R
⊥
, R
⊥
< < R
∼ L
b
,
R
∼ L
b
∼
a
0
R
⊥
, < R
⊥
< R
∼ L
b
.
(12.369)
Combining (12.369) and (12.368) we obtain the
final result for the creep activation energy U
sb
c
of a
vortex superbundle near j
c
,
U
sb
c
∼
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
U
c
L
c
a
0
exp
5c
L
c
a
0
3
, a
0
< R
c
< (a
2
0
)
1/3
,
U
c
L
c
a
2
0
exp
2c
L
c
a
0
3
, R
c
< < (R
3
c
/a
2
0
)
1/2
,
U
c
a
0
3
L
c
a
0
4
, < R
c
.
(12.370)
At small current densities the creep of vortex bun-
dles involves hops beyond andwehavetoextend
the analysis of single vortex creep above using the
general concepts from the theory of dirty elastic
manifolds. In a first step we have to identify the ex-
ponents describing the bundle’s transverse fluctua-
tions u
2
(R, L)≡[u(R, L)−u(0, 0)]
2
on length
scales beyond the pinning lengths R
c
and L
c
,extend-
ing the analysis from the 1 + 2-dimensional vortex
string to 3+2 dimensional vortex manifold.Here, we
can make use of the discussion in Sect. 12.9.1 above,
cf. (12.320), which provides us with the short-range
wandering exponents
SR
1,2
=3/5and
SR
3,2
=1/5(and
correctly reproduces the exact result
1,1
=2/3).Fur-
thermore, on large distances the periodic nature of
the vortex manifold becomes relevant and the im-
pact of disorder decreases as expressed through a
crossover to the Bragg glass scaling regime charac-
terized by the exponent
BG
= 0. Note that the result
for
SR
1,2
=0.600 used here differs by 3 % from the re-
sult
1,2
≈ 0.620derived fromnumericalsimulations
[371,372];thecorrespondingscalingresultsforsingle
vortex creep then take the form L
opt
(j) ∼ L
c
(j
c
/j)
5/7
,
u(j) ∼ (j
c
/j)
3/7
,andU(j) ∼ U
c
(j
c
/j)
1/7
.Wewill use
these results in our interpolation scheme below.
In generalizing the results for the isotropic man-
ifold’s wandering to the vortex lattice with its
anisotropic elastic moduli we interpolate between
the manifold’s short scale fluctuations as given by
(12.325)for the single vortex regime and (12.344) for
the vortex bundle regime (the Larkin results) and
the long distance random manifold and Bragg glass
scaling,
u
2
(R, L)
2
∼
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
L
L
c
2
1,2
, L
c
< L < a
0
,
a
0
L
c
3
ln
1+
R
2
a
2
0
+
L
a
0
2
3,2
, a
0
< R < ,
a
0
L
c
3
R
2
2
+
a
2
0
L
2
4
1/2
2
3,2
, < R < R
a
,
a
2
0
2
ln
1+
R
2
R
2
a
+
a
2
0
L
2
2
R
2
a
, < R
a
< R ,
(12.371)
where the last three expressions refer to the weak
pinning case with L
c
> a
0
. The crossover length
R
a
∼ (L
c
/a
0
)
3
(a
0
/)
1/
3,2
∼ R
c
(a
0
/)
1/
3,2
is ob-
tained by matching the random manifold result in
(12.371) to the Bragg glass scaling at u ∼ a
0
, assum-
ing the crossover takes place in the nondispersive
regime with R
a
> . Note that tracing the growth of
u with distance requires some care; e.g., starting out
in the “strong” pinning regime with L
c
< a
0
the sin-
gle vortex scaling has to be matched to the dispersive
regime using the proper random manifold scaling
expression.
Let us return to the problem of vortex creep at low
drives. We first generalize the free energy (12.357)
for the disordered string to the (isotropic) driven
random manifold,
F(L) ∼ U
c
L
L
c
d,n
−
F
F
c
L
L
c
d+
d,n
, (12.372)
where F and F
c
denote the applied and the critical
force density and
d,n
= d −2+2
d,n
is the energy
exponent.The critical nucleus is characterized by the
size L
opt
(F) and jumps a distance u
opt
(F),
