Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.


XContents
10.9 Conclusions ..................................................................................... 452
References ............................................................................................. 453
11 Universal Properties of Cuprate Superconductors: Evidence and Implications
T. Schneider ..................................................................................... 459
11.1 Introduction .................................................................................... 459
11.2 CriticalBehavioratFiniteTemperature.......................................................... 465
11.3 QuantumCriticalBehaviorandCrossoverPhenomena.......................................... 471
11.4 ThinFilms ...................................................................................... 487
11.5 ConcludingRemarksandComparisonwithOtherLayeredSuperconductors.................... 487
References ............................................................................................. 489
12 Vortex Matter
G. Blatter and V. B. Geshkenbein ................................................................. 495
12.1 Introduction .................................................................................... 496
12.2 Ginzburg–LandauandLondonTheories ........................................................ 502
12.3 VortexLines..................................................................................... 505
12.4 VortexLattice ................................................................................... 512
12.5 LayeredMaterials ............................................................................... 518
12.6 AnisotropicScalingTheory...................................................................... 532
12.7 StatisticalMechanics ............................................................................ 538
12.8 QuenchedDisorder:PinningandCreep ......................................................... 566
12.9 UncorrelatedDisorder:CollectivePinningandCreep ........................................... 575
12.10 CorrelatedDisorder ............................................................................. 605
12.11 SurfaceandGeometricalBarriers ............................................................... 610
12.12 VortexGlasses................................................................................... 615
12.13 ConcludingRemarks ............................................................................ 621
References ............................................................................................. 625
13 Unconventional Superconductivity in Novel Materials
M. B. Maple, E. D. Bauer, V. S. Zapf, and J. Wosnitza .............................................. 639
13.1 Introduction .................................................................................... 640
13.2 ConventionalSuperconductorsContainingLocalizedMagneticMoments ....................... 641
13.3 f -ElectronHeavyFermionSuperconductors..................................................... 659
13.4 OrganicSuperconductors ....................................................................... 696
13.5 LayeredCuprateandRuthenateSuperconductors ............................................... 717
13.6 ComparisonofthePropertiesofDifferentClassesofNovelSuperconductors.................... 741
References ............................................................................................. 744

Contents XI
Volume II. Superconductivity: Novel Superconductors
ListofContributors .................................................................................... XV
14 High-T
c
Superconductivity
H. R. Ott ........................................................................................ 765
14.1 Introduction .................................................................................... 765
14.2 TypicalStructuralCharacteristics ............................................................... 767
14.3 OccurrenceofSuperconductivity................................................................ 774
14.4 PhysicalPropertiesofCopperOxides............................................................ 778
14.5 Physical Properties of Non-Cuprate High-T
c
Superconductors................................... 813
14.6 FinalRemarks................................................................................... 823
References ............................................................................................. 823
15 Tunneling Spectroscopy of Conventional and Unconventional Superconductors
J. Zasadzinski ................................................................................... 833
15.1 Introduction .................................................................................... 833
15.2 BasicTunnelingPhenomenology................................................................ 835
15.3 TunnelingandStrong-CouplingEffects:MicroscopicPicture .................................... 841
15.4 TunnelingSpectroscopyofConventionalSuperconductors ...................................... 844
15.5 TunnelinginHigh-TemperatureSuperconductors............................................... 847
15.6 HeavyFermionSuperconductors................................................................ 861
15.7 OrganicSuperconductors ....................................................................... 862
15.8 OtherMaterials ................................................................................. 863
15.9 Conclusions ..................................................................................... 864
References ............................................................................................. 865
16 Phase-Sensitive Tests of Pairing Symmetry in Cuprate Superconductors
C. C. Tsuei and J. R. Kirtley ...................................................................... 869
16.1 Introduction .................................................................................... 869
16.2 PhaseSensitiveTests:TheoreticalBackground .................................................. 874
16.3 Phase-SensitiveTests:Experiments.............................................................. 880
16.4 Angle-ResolvedDeterminationofGapAnisotropyinYBCO ..................................... 901
16.5 Universality of the d-WavePairState ............................................................ 902
16.6 Implications of d-WavePairingSymmetry ...................................................... 907
16.7 Conclusions ..................................................................................... 912
References ............................................................................................. 913
17 Photoemission in the High-T
c
Superconductors
J. C. Campuzano , M. R. Norma n, and M. Randeria ............................................... 923
17.1 Introduction .................................................................................... 924
17.2 BasicsofAngle-ResolvedPhotoemission ........................................................ 924
17.3 TheValenceBand ............................................................................... 933
17.4 NormalStateDispersionandtheFermiSurface ................................................. 935
17.5 SuperconductingEnergyGap ................................................................... 948
17.6 Pseudogap ...................................................................................... 954

XII Contents
17.7 PhotoemissionLineshapesandtheElectronSelf-Energy ........................................ 963
17.8 Summary........................................................................................ 987
References ............................................................................................. 988
18 Neutron Scattering and the Magnetic Response of Superconductorsand Related Compounds
S. M. Hayden .................................................................................... 993
18.1 Introduction .................................................................................... 993
18.2 TheNeutronScatteringTechnique .............................................................. 994
18.3 TheStaticSpinSusceptibilityofSuperconductors ............................................... 999
18.4 Magnetic Excitations in Metals and Weakly Coupled Superconductors. . .. . .. . .. . .. . . . . . . . . . . . . . .1001
18.5 Excitations and Superconductive Pairing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . .1003
18.6 High Temperature Superconductivity . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . ..1004
18.7 Discussion .. . .. . .. . .. . .. . . . . . . . . . .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . . . . . . .. . .. . ..1023
18.8 Final Remarks . . . .. . .. . . . . . . . . . .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . . . . . . . . . .. . .. . ..1024
References . . . . . . . .. . .. . .. . .. . . . . . . . . . .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . . . . . . .. . .. . .. . ..1024
19 Heavy-Fermion Superconductivity
P. S. Riseborough, G. M. Schmiedeshoff, and J. L. Smith .. . .. . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . .. . . .1031
19.1 Overview . . .. . .. . .. . .. . . . . . . . . . .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . . . . . . .. . .. . .. . ..1031
19.2 Introduction . . . . . . . . . . . . .. . .. . . . . .. . . . . .. . . . . .. . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . ..1033
19.3 Properties of the Normal State .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . . . . . . . . . .. . .. . ..1069
19.4 PropertiesoftheSuperconductingState.........................................................1103
19.5 Heavy Fermion Superconducting Compounds . . . . . . . . . . . .. . .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1132
19.6 The Conclusion . . . . . . . . . .. . .. . .. . . . . . . . . . . . . . . . . .. . .. . . . . . . . . . . . . .. . .. . .. . .. . . . . . . . . . .. . .. . .. . . .1140
References . . . . . . . .. . .. . .. . .. . . . . . . . . . .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . . . . . . .. . .. . .. . ..1141
20 Organic Superconductors
M. Lang a nd J. M¨uller . . . .. . .. . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . .. . . . .. . .. . . . . . . . . .1155
20.1 Introduction . . . . . . . . . . . . .. . .. . . . . .. . . . . .. . . . . .. . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . ..1155
20.2 Characteristics of Organic Charge-Transfer Conductors .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1157
20.3 Normal-State Properties . . . . . . . . . . .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . . . . . . .. . .. . ..1162
20.4 Superconducting-State Properties .. . . . . .. . .. . .. . . . . . . .. . .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..1182
20.5 Epilogue . . . . . . . . .. . . . . . . .. . . . . . . . . . . .. . . . . . . . . . . . . . .. . . . . . . .. . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . .. 1212
References . . . . . . . .. . .. . .. . .. . . . . . . . . . .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . . . . . . .. . .. . .. . ..1214
21 Concepts in High Temperature Superconductivity
E.W. Carlson, V. J. Emery, S.A. Kivelson, and D. Orgad .. . . . . . . . . . . . . . .. . . . . . . . . . . .. . . . . . . .. . .. . . .1225
21.1 Introduction . . . . . . . . . . . . .. . .. . . . . .. . . . . .. . . . . .. . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . ..1227
21.2 High Temperature Superconductivity is Hard to Attain .. . . . . . . . . . . . . .. . .. . .. . . . . . . .. . .. . .. . . . . . .1230
21.3 Superconductivity in the Cuprates: General Considerations .. . .. . .. . .. . . . . . . . . . . . . .. . . . . . . . . . . . .1234
21.4 Preview: OurView of the Phase Diagram . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1244
21.5 Quasi-1D Superconductors . .. . . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . . . . . . . . . . . . . .1245
21.6 Quasi-1D Physics in a Dynamical Stripe Array . . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1257
21.7 Electron Fractionalization in D > 1 as a Mechanism of High Temperature Superconductivity . . .1259
21.8 Superconductors with Small Superfluid Density . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . ..1262
21.9 Lessons from Weak Coupling .. . . . . . . . . . . . . . . . .. . .. . .. . . . . . . . . . . . . .. . .. . .. . . . . . . . . . .. . .. . . . . . . . . .1272
21.10 Lessons from Strong Coupling . . . . . . . . . . .. . .. . .. . . . . . . .. . .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..1277

Contents XIII
21.11 Lessons from Numerical Studies of Hubbard and Related Models . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1286
21.12 Doped Antiferromagnets . . . .. . .. . . . . . . . . . . . . . .. . .. . . . . . . .. . .. . . . . . . . . . . . . . .. . .. . . . . . . .. . .. . . . . . .1300
21.13 Stripes and High Temperature Superconductivity . . . . .. . .. . .. . .. . .. . .. . . . . . . . . . . . . .. . .. . .. . .. . ..1310
References . . . . . . . .. . .. . .. . .. . . . . . . . . . .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . . . . . . .. . .. . .. . ..1327
22 A Spin Fluctuation Model for d-Wave Superconductivity
A. V. Chubukov, D. P ines, and J. Schmalian . . . . . . . .. . . . . . . .. . .. . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . ..1349
22.1 Introduction and Overview. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . ..1349
22.2 Spin–Fermion Model . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . .. . . . . .. . . . . .. . . . . . . . . . . . . . . . . .1358
22.3 Summary of Strong-Coupling Theory for Electron–Phonon Pairing . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1363
22.4 Strong-Coupling Approach to Spin–Fermion Interaction . . . . . . . . . .. . .. . .. . . . . . . . . . .. . .. . . . . . . . . .1366
22.5 Fingerprints of Spin Fermion Pairing.. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . ..1377
22.6 Comparison with the Experiments on Cuprates . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . . . . . . . . .1389
22.7 Conclusions . . .. . .. . .. . .. . . . . . . . . . .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . . . . . . .. . .. . ..1403
22.8 Note Added . . .. . . . . . . . . . . . . . . . . . . .. . .. . . . . . . . . . . .. . . . . . . .. . .. . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . .. 1405
References . . . . . . . .. . .. . .. . .. . . . . . . . . . .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . . . . . . .. . .. . .. . ..1407
23 Electronic Theory for Superconductivity in High-T
c
Cuprates and Sr
2
RuO
4
D. Manske, I. Eremin, and K. H. Bennemann . . . . . .. . . . . . . .. . . . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . ..1415
23.1 Introduction . . . . . . . . . . . . .. . .. . . . . .. . . . . .. . . . . .. . . . . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . ..1416
23.2 Electronic Theory for Hole-Doped and Electron-Doped Cuprates . . . . . . .. . .. . .. . . . . . . .. . . . . . . . . .1428
23.3 Electronic Theory for Ruthenates (Sr
2
RuO
4
). . . . . . . . . . . . . . . . .. . .. . . . . . . . . . . .. . . . . . . .. . .. . . . . . . . . .1451
23.4 ResultsforHole-DopedandElectron-DopedCuprates...........................................1460
23.5 Results for Sr
2
RuO
4
.. . . . . . . .. . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . .. . . . . . . .. . .. . . . . . . . . .1485
23.6 Summary and Outlook . . . . . . . . . . . .. . . . . . . . . . . .. . . . . . . .. . .. . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . .. . . .1496
Appendix...............................................................................................1497
References . . . . . . . .. . .. . .. . .. . . . . . . . . . .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . . . . . . .. . .. . .. . ..1511
24 Superfluid
3
He and the Cuprate Superconductors
A. J. Leggett . . . . . .. . . . . . . .. . .. . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . . .. . . . .. . .. . . . . . . . . .1517
24.1 Introduction: Bose Condensation and Cooper Pairing .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1517
24.2 The Normal State: Is the Fermi-Liquid PictureValid? . .. . . . . . . . . . . . . . . . . .. . .. . .. . .. . . . . . . . . . .. . ..1522
24.3 Response Functions:The MIR Peak in the Cuprates . . .. . .. . .. . .. . .. . . . . .. . . . . .. . .. . . . . . . . . . . . . . .1525
24.4 The Cooper-Paired States of Superfluid
3
He and the Cuprates: General Considerations . . .. . .. . ..1526
24.5 Symmetry of the Order Parameter. . . . . . . . . . . . . . . .. . . . .. . .. . . . . . . . . . . .. . .. . . . . . . . . . . . . . . . . . . .. . . .1531
24.6 Conclusion . . . . . . . . . .. . .. . . . . . . . . . . . . .. . .. . .. . .. . . . . . . .. . .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ..1534
24.7 Summary. . . . . .. . .. . . . . . . .. . . . . . . . . . . .. . . . . . . . . . . . . . .. . . . . . . .. . . . . . . . . . . . . . .. . . . . . . .. . . . . . . . . . . . .1534
References . . . . . . . .. . .. . .. . .. . . . . . . . . . .. . .. . .. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .. . .. . .. . .. . . . . . . .. . .. . .. . ..1535
Author Index . . . . . . . . . . . .. . .. . . . . . . .. . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . .. . . . . . . .. . .. . . . . . . . . .1537
Subject Index . . . . . . . . . . . . . .. . . . . . . .. . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . .. . . . . . . .. . .. . . . . . . . . .1545

List of Contributors
Bauer, E.D.
Department of Physics and
Institute for Pure and Applied Physical Sciences,
Univ. of California,
San Diego La Jolla,California, USA
ericb@physics.uscd.edu
Bennemann, K.H.
Institut f¨ur Theoretische Physik,
Freie Universit¨at Berlin,
Berlin, Germany
khb@physik.fu-berlin.de
Blatter, G.
Theoretische Physik
ETH H¨onggerberg,
CH-8093 Z¨urich,Switzerland
blatterj@itp.phys.ethz.ch.
Buzdin, A.I.
Inst. Univ. de France and Univ. Bordeaux,
Talence, France
a.bouzdine@cpmoh.u-bordeaux1.fr
Carbotte, J.P.
McMaster University, Physics Dept.
Hamilton, Ontario L8S 4M1, Canada
carbotte@mcmaster.ca
Chandrasekhar, V.
Dept. of Physics, Northwestern University,
Evanston,Illinois,USA
v-chandrasekhar@nwu.edu
Deutscher, G.
School of Physics and Astronomy,
Department of Condensed Matter Physics,
Tel Av iv Universi ty,
Tel Av iv, Israel
guyde@post.tau.ac.il
Geshkenbein, V.B.
ETH Z¨urich, Theoretische Physik,
H¨onggerberg CH-8093, Z¨urich, Switzerland
dimagesh@itp.phys.ethz.ch
Gor’kov, L.
Florida State University,
Nat. High Magnetic Field Laboratory, Jamaica Ct.
Tallahassee, FL 32308
gorkov@magnet.fsu.edu.
Ketterson, J.
Dept.ofPhysics,Northwestern
University, Evanston, Illinois, USA
j-ketterson@nwu.edu
Kuli´c, M.L.
Brookhaven Natl. Lab.,
Upton, New York, USA and
Max-Planck Institute – Physics of Complex Systems,
Dresden, Germany
kulic@itp.uni-frankfurt.de
Larkin, V.A.
University of Minnesota,Laboratory of Physics,
146 Tate St. SE Minneapolis, MN 55455, USA
vlarkin@physics.spa.umn.edu

XVI List of Contributors
Maple, M.B.
Dept. of Physics and
Inst. for Pure and Applied Physical Sciences,
Univ. of California,
San Diego La Jolla,California, USA
mbmaple@ucsd.edu
Marsiglio, F.
University of Alberta,
Dept. of Physics
Edmonton, AB T6G 2JI, Canada
frank.marsiglio@phys.ualberta.ca
Morr, D.
University of Illinois at Chicago,
Dept.ofPhysics,USA
dkmorr@uic.edu
Pitaevskii, L.
University of Trento,
Dept. of Physics
I-38050 Povo (Trento), Italy
lev@science.unitn.it.
Schneider, T.
Physik–Institut der Universit¨at
Z¨urich, Switzerland
tschnei@physik.unizh.ch
Shafranjuk, S.E.
Dept.ofPhysics,Northwestern
University, Evanston, Illinois, USA
Va r la mov, A . A .
COHERENTIA-INFM, CNR
Rome, Italy
varlamov@ing.UniRoma2.it.
Wosnitza, J.
Institut f¨ur Angewandte Physik,
TU Dresden,
Dresden, Germany
wosnitza@physik.tu-dresden.de
Zapf, V.S.
Dept. of Physics and
Inst. for Pure and Applied Physical Sciences,
Univ. of California,
San Diego La Jolla,California, USA
vzapf@physics.ucsd.edu

Volume I
Superconductivity:
Conventional and Unconventional Superconductors
1 History of Superconductivity:
Conventional, High-Transition Temperature and Novel Superconductors
K. H. Bennemann Dept.ofPhysics,FreieUniversit¨at Berlin, Germany
J.B. Ketterson Dept. of Physics and Astronomy, Northwestern University, Evanston, USA
1.1 Introduction ................................................................................3
1.2 Novel Superconductors .......................................................................9
1.3 Granular Superconductors, Mesoscopic Systems, Josephson Junctions ............................18
1.4 Outlook ....................................................................................23
References.................................................................................25
1.1 Introduction
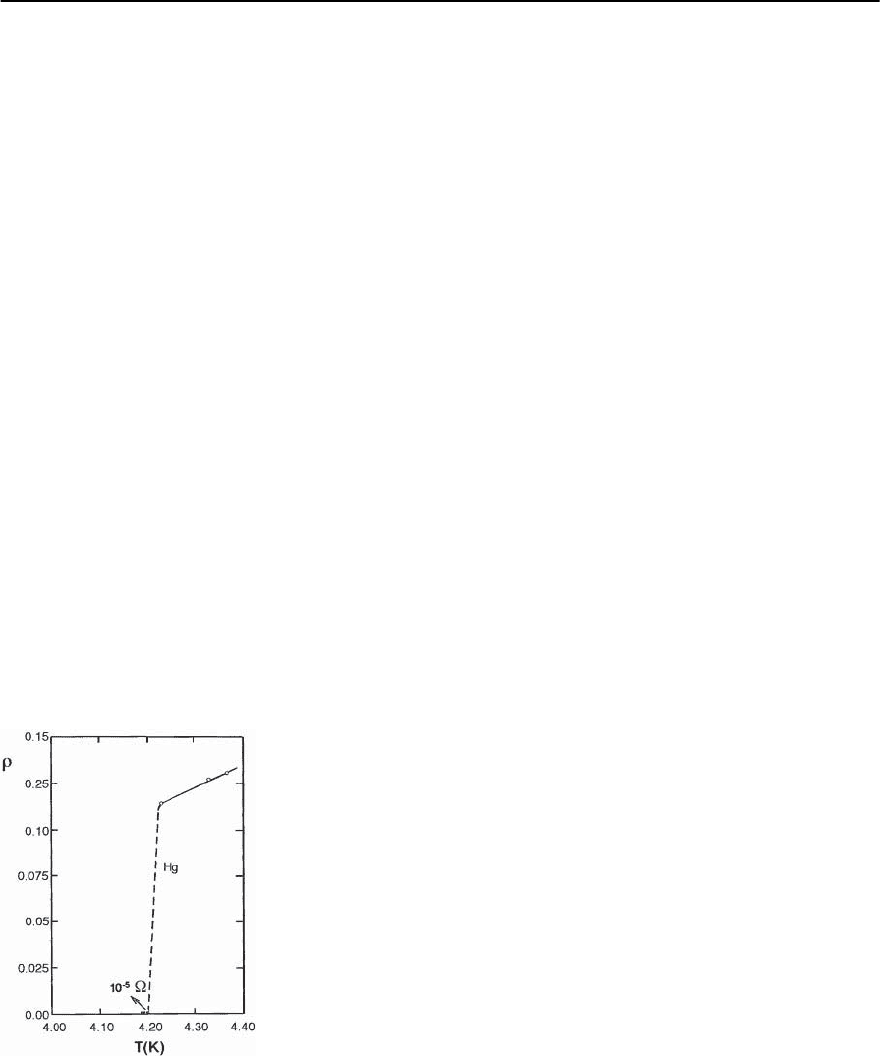
Since its discovery by H. Kamerlingh Onnes in Lei-
den [1] almost 100 years ago, superconductivity has
remained an important area of solid state physics
with continuing surprises.Its first observation in Hg,
illustrated for historical reasons in Fig. 1.1, resulted
from general advances in low temperature physics
(liquefying He).The important continuingdiscovery
Fig. 1.1. Illustration of Kamerlingh Onnes’ discovery of su-
perconductivity and vanishing of the electrical resistivity
in 1911
of new superconductors resulted from advances in
material science physics. By 1980 superconductivity
hadbeen observed in manymetals andalloys thereof.
ForanillustrationseeFig.1.2[2].Remarkably,the
classical ferromagnets like Ni, Fe, etc. did not exhibit
superconductivity. Only for the non-magnetic state
and under (strong) pressure has superconductivity
been reported (for example in iron, T
c
= 2K) [3].
From the beginning a strong motivation was to find
superconductors with a high transition temperature
T
c
. However, until about 1980 the A-15 compound
Nb
3
Ge remained the superconductor with the high-
est T
c
at about 30 K, see Fig. 1.3. In order to achieve
higher T
c
values also many alloys and the effect of
applying pressure were studied.
Soon after 1980 exciting new superconductorsbe-
longing to rather different material classes were dis-
covered. The situation including the high T
c
cuprate
superconductors discovered by Bednorz and M¨uller
[4] in 1986 is illustrated in Fig. 1.4. For several rea-
sons this tremendously stimulated the minds of the
physics community. High-T
c
cuprate superconduc-
tivity exhibited puzzling new behavior. Perhaps this
helped the birth of new surprises which were yet to
come.
One may note that the history of superconductiv-
ity exhibits similar alternating periods of great ex-
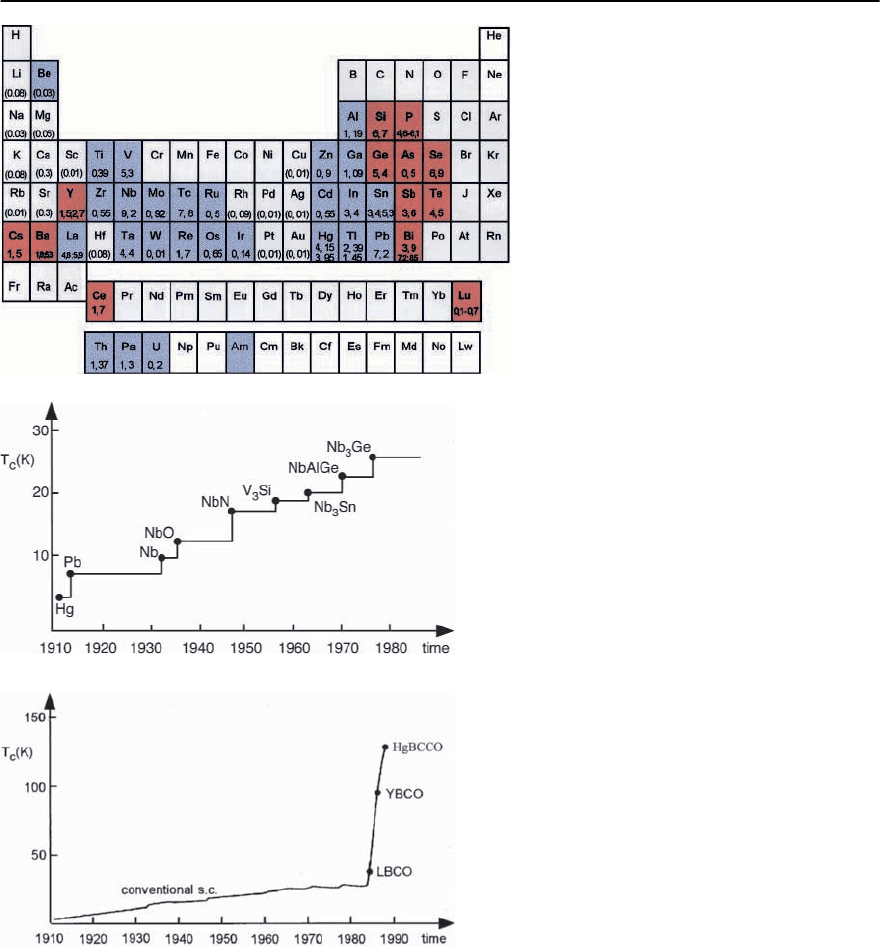
4 K.H. Bennemann and J.B.Ketterson
Fig. 1.2. Overview of superconducting metals
(blue) in the periodic table. Note the absence of
superconductivity in the ferromagnetic transi-
tion metals and rare-earth and actinide metals.
Other superconductors (under pressure) are
marked in red. The superconducting transition
temperature T
c
is indicated
Fig. 1.3. Historyof the transition temperature T
c
for the
first 70 years following the discovery of superconduc-
tivity in 1911. The A-15 compounds were of particular
interest in the search for higher T
c
-superconductors
Fig. 1.4. High-T
c
cuprate superconductors discovered
by Bednorz and M¨uller in 1986. For La
2−x
Ba
x
CuO
4
a
T
c
35K, for YBa
2
Cu
3
O
7−ı
a T
c
=92K,andfor
HgBa
2
Ca
2
Cu
3
O
8+ı
a T
c
= 133K was observed, for ex-
ample
citement and phases that were more quiet, as was
the case for other important classical problems in
physics. Generally, the study of superconductivity
was a motor for new experimental techniques as well
as for methods in theoretical physics, in many-body
physics and quantum field theory, and was responsi-
ble for new concepts of quite general significance in
physics. The noticeable interplay of experiment and
theory was particularly fruitful as history shows, in
particular regarding the electronic mechanism for
phonon-mediated superconductivity and the sym-
metry of the superconducting state.

1 Historyand Overview 5
Fig. 1.5. Meissner effect for type I superconductors: If a
superconductor in an external magnetic field H is cooled
below its superconducting transition temperature T
c
,the
magnetic flux B is abruptly expelled. For particular val-
ues of B it penetrates the superconductor only within the
penetration depth at the surface (B = H +4 M)
Cornerstones in the early history of superconduc-
tivity were:
1. Observation of vanishing resistivity (R)ata
critical temperature T
c
4.2KinHgbyKamer-
lingh Onnes [1] in 1911.
2. Observation of the diamagnetic behavior of type
I superconductors by Meissner and Ochsenfeld
in 1933,which opened the way towards a deeper
understanding of superconductivity;see Fig. 1.5
for an illustration of the Meissner effect [5].
3. The London theory in 1935, whichdescribed the
Meissner effect flux repulsion, by using for the
superconducting current driven by the vector
potential A the formula [6]
j
s
=−
c/4
2
L
A , (1.1)
with
L
=(mc
2
/4e
2
n
s
)
1/2
,andn
s
the den-
sity of the superfluid. Then, from rotj
s
and the
Maxwell equations one gets the Meissner effect
(see (4/c)rotj
s
= ∇×∇×B).
4. The Isotope effect [7], T
c
∝ M
−˛
, ˛ ≈ 0.5 for
Hg, observed by Maxwell 1950 and which sug-
gested that the electron–phonon coupling might
be responsible for superconductivity.
5. The Ginzburg–Landau theory in 1950, whichex-
tended the London theory and introduced the
order parameter [8]
(r, t)=| | e
i' (r )
, (1.2)
with n
s
∝| |
2
and
j
s
=2e | |
2
v
s
=
2e
m
∗
| |
2
∇' −
2e
c
A
.
(1.3)
6. The breakthrough by the famous and most ele-
gant theory of Bardeen, Cooper, Schrieffer (BCS)
in 1956 which after almost 45 years gave a defi-
nite electronic explanation of superconductivity
in terms of Cooper pairs (k ↑, −k ↓)forming
in an energy shell !
D
(!
D
denotes the Debye
frequency) around the Fermi energy "
F
resulting
from the electron–phonon interaction [9].
The BCS theory became one of the most elegant and
successful theories in physics [9]. It was further com-
pleted by the field theoretical approaches of Gor’kov
[10], Abrikosov and Gor’kov [11], and Eliashberg
[12]. Important in understanding (magnetic) field-
dependence was Abrikosov’s analysis based on the
Ginzburg–Landau theory of type I superconductors
( < 1/
√
2, ≡ /, is the penetration depth, the
coherence length referring to the stiffness of )and
type II ones ( > 1/
√
2), which allow magnetic flux
to penetrate the superconductor in a regular array,
quantized in units of the elementary flux quantum
0
= hc/2e [13]. Important was also the observation
of flux quantization in a ring, flux =(n +
1
2
)
hc
e
,
(n =0, ±1,...), by Doll and N¨abauer, and Deaver
and Fairbank [16]. This is illustrated in Fig. 1.6.
A further step was Josephson’s tunneling theory
in 1962 describing also tunneling of Cooper pairs
through a barrier between two superconductors[14].
The current is given by j (t)=j
0
+ j(' ), where
' = '
2
− '
1
is the phase difference between the
two superconductors 1 and 2 separated by a tunnel
barrier (' = '
0
2
− '
0
1
−(2ec)
2
1
dxA
x
). Then one
may get for the Cooper pair current (A =0andvolt-
age V)
j(t)=j
0
+ j
1
sin
'
0
2
− '
0
1
−
2e
V
21
t
,
V
21
=
2e
˙'
21
. (1.4)
Very important was also the study of the tunneling
density of statesby Schrieffer, Scalapino andWilkens
