Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

550 G. Blatter and V.B. Geshkenbein

wherewehaveassumedthata

<  in the last equa-

tion. For a strong interlayer coupling the above con-

ditions require a

<  <  < 

/ while a weak

coupling requires a

< 

/ <  < . The high-

field decoupling line then takes the form

(T) ∼ B







B > B

≈ B



,  <  ,

B > B

≈ B







,  <  ,

(12.227)

with the usual definitions B



≡ ¥

/

and B



≡

/

; note that with decreasing coupling strength

(increasing ) the crossover field B

first decreases

to approach B



at  ≈  and then increases again as

 increases further; since B > B



we are allowed to

approximate 1 + g ≈ 1 in this regime, as assumed in

the beginning.

For strong coupling  <  andintermediatefields

 < a

< 

/ the shear term ∝ K

and the electro-

magnetic energy ∝ K

lose the competition against

the Josephson couplingand the decoupling line takes

the form

(T) ∼ B



B < B



,  <  or  <  . (12.228)

The same result is obtained in the low-field regime



/ < a

whenever the Josephson interaction out-

plays the electromagnetic coupling, whichis the case

whenever B drops below B



.This completes the anal-

ysis for the strong coupling situation.

For weak coupling ( < ) and intermediate

fields B



< B < B

(i.e., 

/ < a

< ) the phase

ﬂuctuations are limited by the electromagnetic in-

teraction. The ∝ K

term in (12.226) is dominant

between the lower cutoff K

min

∼ (1 + g)/g

set

by the Josephson term and the upper cutoff deter-

mined by either the Brillouin zone boundary with

max

∼ 1/a

or by the shear term, in which case

max

∼ g/(1 + g)a

; correspondingly we find the

mean squared ﬂuctuation



ı'



≈

1+g

⎧

⎪

⎨

⎪

⎩

, B



< B < B



, B



< B < B



(12.229)

Comparing to more sophisticated calculations (cf.

Sect. 12.7.5 below) we find that the logarithm in

(12.229) is a peculiarity of the Lindemann analysis

andactually shouldbe replaced bya number ˛,hence

the low-field decoupling line assumes the form,

(T) ≈



˛



1−

˛T





< B < B

,  <  , (12.230)

where the factor [1 − ˛T/4"

d]appearsasacon-

sequence of the renormalization of the superﬂuid

density through the factor g/(1 + g). Note that the

above weak-coupling result B

does not depend on

the anisotropy parameter ".

The Lindemann criterion cannot tell us about the

underlying mechanism triggering the transition (in

fact, the Lindemann criterion assumes that the tran-

sition follows from a trivial increase in the ﬂuctua-

tion amplitude). We will see later (cf. Sect. 12.7.5 be-

low) that in the low coupling limit " → 0thedecou-

pling transition assumes a topological character and

is triggered by the appearance of vortex loops,either

in the form of interstitial/vacancy pancake-vortex

pairs(these correspondto vortexloopsin planesper-

pendicular to the layers) or in the form of Josephson

vortex loops (i.e., loops parallel to the layers). The

defect transition is of the Kosterlitz–Thouless type

(cf. Sect. 12.7.5) and appears at B

(T)asgivenby

(12.230) with ˛

def

= 8. The position of the loop tran-

sition has been determined via a self-consistent cal-

culation of the inter-layer coupling [73] and later via

a renormalization group approach [75],

(T)=B



T

B ≤ B

≈ B







,  <  . (12.231)

Again,thisresult followsthe Lindemann line (12.230)

if we set ˛

= 1 (the additional factor (1 − T/4"

d)in

(12.230) is due to the renormalization of the super-

ﬂuid density which has not been taken into account

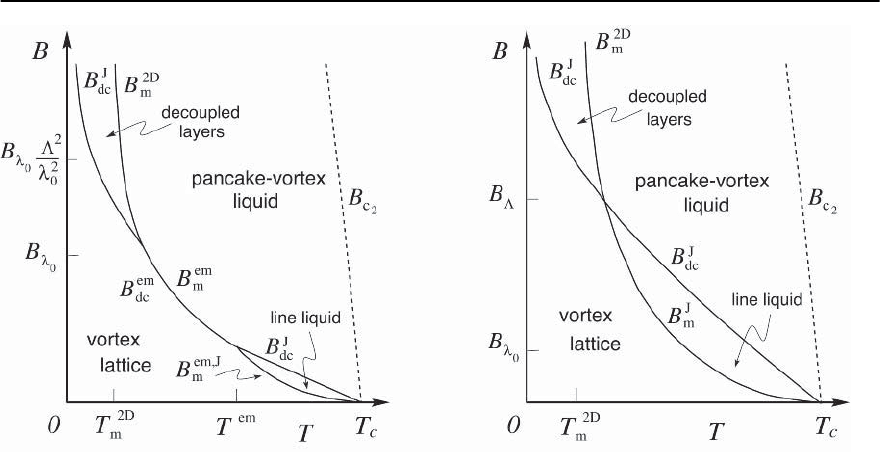
12 Vortex Matter 551

Fig. 12.13. Schematic low-field phase diagrams of layered superconductors with melting and decoupling lines. At high

fields/low temperatures the phase ﬂuctuations triggering decoupling are limited by shear modes,while tilt modes are rele-

vant in the low-field/high-temperature region close to T

.Left:Forweakcoupling <  the decoupling and melting lines

merge at intermediate temperatures with a joint transition at the electromagnetic melting/decoupling line B

= B

With increasing coupling, T

→ 0 and the common melting/decoupling transition at B

m,dc

disappears as the transition

rises above the B



line for  <  (right). It is unclear whether the decoupling line in the vortex liquid corresponds to a

real phase transition or a mere crossover

in [73,75]). Since the defect transition involves an

eight times larger value of ˛, it preempts the Joseph-

son loop transition and the true decoupling is trig-

gered by the proliferation of free interstitials and va-

cancies in the small " limit.

Finally,let us combinethe above results for the de-

coupling transition with those obtained previously

for the melting transition and construct the corre-

sponding B–T phase diagram, cf. Fig. 12.13. Starting

from the small coupling limit " → 0,  < ,we

notethat the low-fieldexpression (12.230)forthe de-

coupling line B

coincides (up to a factor of order

unity) with the form of the electromagnetic melting

line B

, see (12.212), suggesting that the two tran-

sitions may join up within the temperature regime

< T < T

[249]. Indeed, we will see below

in Sect. 12.7.5 that the melting line undercuts the

decoupling line and the two transitions merge into

a single one. As the temperature increases beyond

the Josephson interaction becomes relevant and

decoupling occurs in the liquid phase following B

as given by the low-field result (12.228) above, see

Fig.12.13.Note that the interlayer phase ﬂuctuations

are limited by tilt interactions in the low-fieldregime

where the decoupling occurs in the liquid phase, giv-

ing some justification to the application of (12.226)

in the liquid regime.On the other hand, the primary

expression (12.226) has been derived with the crys-

tal as a starting point (i.e., a well defined displace-

ment field u) and it remains unclear how much the

result of a second transition in the liquid can be

trusted. In fact, many suggestions have been made

regarding the existence of intermediate vortex liquid

phases [287,288] but a final conclusion has not been

reached(note that the various proposed intermediate

liquid phases involve layered and anisotropic super-

conductors as different starting points; e.g., the de-

coupling line (12.228) involves the layer separation d

and does not scale in the parameter T/").

552 G. Blatter and V.B. Geshkenbein

Increasing the layer coupling the branching point

at T

moves down in temperature and joins up

with the point where decoupling and melting merge

at low temperatures. The intermediate line B

m,dc

squeezed as the melting/decoupling transition rises

above the B



line. The phase diagram then simplifies

in the regime  <  with a simple cutting of the

melting and decoupling lines in the vicinity of the

point (T

, B



) [71], see Fig. 12.13.

12.7.4 Vortex Lattice Melting in 2D Thin Films

An attractive scenario for the melting of 2D crystals

has been put forward by Nelson and Halperin [289]

who base their analysis on the unbinding of dislo-

cation pairs in the framework of a BKT transition.

This concept has later been applied to the 2D vor-

tex system in thin superconducting films [235,236]

(however, we remind that numerical simulations

[273–275] suggest 2D vortex lattice melting to be

first-order). The role of the logarithmically inter-

acting topological excitations is played by the edge

dislocations. Using a continuum description, the dis-

placement field of an edge dislocation with a Burgers

vector b =(b, 0) pointing along the x-axis is given

by [171,290]

dis

2



+arctan

, −



(12.232)

and the energy associated with this defect is

dis

(R)=







∇

⊥

· u

dis

)

2

. (12.233)

The lower cutoff R

is provided by the lattice constant

of the vortex lattice, whereas the upper cutoff R

is given either by the sample dimension L (→ self-

energy of the topological defect) or by the distance

R to the nearest dislocation with an opposite Burgers

vector (→ logarithmic interaction between two op-

positely“charged”topological excitations).Note that

the distortion (12.232) does not involve any com-

pression (∇·u

dis

= 0) but only shear forces, a conse-

quence of the incompressibility of the vortex lattice,

 c

. For an elementary dislocation the Burgers

vector (the misfit-vector when encircling the dislo-

cation) is equal to a unit lattice vector and the energy

dis

(R) becomes



dis

(R)=

√

3

, (12.234)

which isa factor4

√

3 ≈ 7 smaller than the corre-

sponding energy (12.195) for the vortex excitation

itself. The BKT-type dislocation-mediated melting

transition of the 2D vortex lattice then takes place

at a temperature [235,236]



4

≈

√

3

≈

 T

BKT

. (12.235)

The numerical A ≈ 0.62 accounts for the renor-

malization of the shear modulus c

due to bound

dislocation pairs [269]. Vortex lattice melting in

thin Nb

Ge films following the dislocation-mediated

melting scenario has been observed by Berghuis,van

der Slot, and Kes [291].

The usual dislocation-mediated melting scenario

predicts a two-step transition [289,292]: The low-

temperature phase is characterized by quasi-long-

range translational order with a density–density cor-

relator





(R)

−K



(0)

=exp



−K



[u(R)−u(0)]





(12.236)

∝ R

−



, 



(T)=



4c

, (12.237)

(here, 



(R)=exp{iK



· [R + u(R)]} and we

have used [u(R)−u(0)]



∼ 2u

(R)

(T/c

d)ln(R/a

)) decaying algebraically with dis-

tance and producing algebraic Bragg peaks in the

structure factor,



(K) ∝|K − K



−2+



. (12.238)

In addition, the 2D crystal exhibits orientational

long-range order as quantified by the angle correla-

tor ¦

(R)¦

∗

(0)

, ¦

=exp[in (R)] with the bond-

angle field (R)=(@

− @

)/2. In the first step

of the melting process, dislocations unbind at T

and destroy the translational quasi-long-range or-

der, while orientational long-range order transforms

into quasi-long-range order, ¦

(R)¦

∗

(0)

∝ R

−

with 

=18T/K

the Franck constant describ-

ing the stiffness of the bond-angle field (R). This

12 Vortex Matter 553

intermediate phase is the hexatic liquid. The melt-

ing is completed in a second BKT type transition (at

= K

/72) where disclinations unbind(a dislo-

cation can be viewed as a tightly bound pair of discli-

nations),destroying the hexaticquasi-long-rangeor-

der in the bond-angle field.This“classic”topological

melting scenario is modified for high fugacities of

the dislocations, implying a large density of dislo-

cation pairs at the transition. The two continuous

transitions described above then collapse into a sin-

gle first-order transition [271–275] and the melting

transition is more conventional (a similar collapse is

familiar from the merging of the two critical fields

and H

into the first-order transition at H

 = / decreases below the value 1/

√

2).

12.7.5 Electromagnetically Coupled Layered

Superconductors

The extreme case of a layered superconductor is

a stack of 2D superconducting films without any

Josephson coupling between the layers. This limit is

difficult to realize in a material as even a weak cou-

pling " ∼ 10

−3

already has an appreciable effect on

the phase diagram,cf.Fig.12.11; materialsapproach-

ing this limit are the layered BiSCCO compound and

the artificially grown multi-layer structures such as

the (Y/Pr)Ba

7−y

[188] and the Mo

1−x

/Ge

[189] systems. The interaction between pancake vor-

tices is of electromagnetic origin (see (12.126)): the

logarithmic intra-plane repulsion between pancake

vortices extends to infinity, V

(R)=−2"

ln(R/L)

(cf. (12.122), L denotes the system-size cutoff) and

the attractive inter-layer interaction is small by the

small factor d/ but long-ranged,extending over/d

layers (cf. (12.130)). The resulting line elasticity is

strongly dispersive,

≈

2





1+



. (12.239)

Note that short wavelength distortions with a

large k

∼ 1/d produce a potential energy

d ln(/d)(u/)

(this energy results from adding

the pairwise interaction energy (12.130) over /d

pairs),while long wavelength(k

< 1/)ﬂuctuations

of a vortex line involve the elastic energy ∼ "

An individual stack of pancake vortices already

defines an interesting thermodynamic system: ther-

mal ﬂuctuationsblur the vortex line and even trigger

its evaporation at high temperatures [65]: pulling a

pancake-vortex out of its stack costs the logarith-

mic energy 2"

d ln(u/) [65] and the usual energy-

entropy argument predicts a vortex-line evaporation

at T

evap

= T

BKT

= "

d(T

BKT

)/2. Note that with the

appearance of free vortices through vortex-pair un-

binding atT

BKT

the concept of a pancake vortex stack

looses its meaning; thisis consistentwith its evapora-

tion at T

evap

= T

BKT

.Thisstackevaporationisreadily

rederivedthrougha self-consistency argument [293];

the latter provides the basis for the self-consistent

substrate model [294] used below in the derivation

of the pancake-vortex lattice melting transition.

Each pancake vortex of the stack is subject to a

quadratic potential

(u)=

(12.240)

produced by the other members of the stack. The pa-

rameter ˛

of this “substrate potential” is given by

the thermal average (cf. (12.148) where we have in-

troduced the elastic energy v

≈ ˛

; here,we ac-

count for the thermal renormalization of this quan-

tity)



n=0

@

int

− u

, nd)

. (12.241)

Given the long-range nature of the pancake-vortex

interaction, we can ignore correlations in the

pancake-vortex ﬂuctuations and hence

(u



−



n=0



(2)

int

(K, nd)e

−K

u



≈

2"



(2)

exp(−K

u



/2)

1+

≈

u



⎧

⎪

⎨

⎪

⎩

u



2

u



, u



 2

1−

2

u



, 2

u



(12.242)

554 G. Blatter and V.B. Geshkenbein

with the pancake-vortex interaction energy

int

(K, nd)=¥



(dk

/8

) k

/[K

(1 +



)] exp(ik

nd) deriving from (12.126). On the

other hand, the equipartition theorem for a har-

monic potential tells us that u



=2T/˛

.The

two expressions for ˛

(u



) cut at a finite value

u



< ∞ if T < "

d/2; approaching T → "

d/2,

u



> 2

becomes large and we can find the

precise solution using the asymptotic expression in

(12.242). The mean square displacement

u



2

1−2T/"

(12.243)

diverges at T

BKT

= "

d(T

BKT

)/2 and the pancake vor-

tex stack evaporates.

The discussion above and in Sect. 12.7.4 provides

us with two important results [294]: First, we know

the position of the melting line for the pancake-

vortex lattice in the two limits of high and low fields

(ignoring reentrance in the latter case). For high

fields B  ¥

/

= B



thein-planerepulsionis

the dominant interaction between pancake vortices

and the melting process exhibits a 2D character: the

lattice melts as the temperature is increased beyond

≈ "

d/70.In BiSCCO the penetration depth is of

order (0) ≈ 2000 Å and d ≈ 15 Å, "

d ≈ 750 K, and

the high-field limit of the melting line approaches

≈ 11 K. At low fields, the electromagnetic in-

teraction between pancake vortices in different lay-

ers is dominant. In the limit B → 0 we can ignore

the interaction between pancake-vortex stacks and

these stacks melt or evaporate at T

BKT

(note that

the true melting line will reenter before reaching the

stack evaporation temperature); for BiSCCO we have

BKT

≈ 0.9 T

(note, however, that Josephson cou-

pling cannot be ignored in BiSCCO, hence one has

to expect that the low-field melting line is pushed

closer to T

). Second, we have learnt how to use a

self-consistent substrate model for an accurate de-

scription of the evaporation transition of an individ-

ual pancake-vortex stack — below we will generalize

this idea to describe the melting (evaporation) of the

pancake-vortex lattice.

Pancake-Vort ex Lattice Melting

Knowing the position of the melting line in the two

limits of high and low fields (up to reentrance), the

question is how to obtain the line in between. Here,

we can make use of the above analysis: The self-

consistent substrate model accurately describes the

melting/evaporation of a single pancake-vortex stack

(a self-consistent harmonic approximation has been

used in the analysis of the 2D XY-model [295]). The

idea then is to extend this analysis to the 3D pancake-

vortex system at finite fields.Let us choose one of the

layers (say n = 0) as our reference, then the pancake

vorticesin the otherlayersformstackswhichprovide

a periodic substrate potential in which the pancake

vortices of our reference layer are trapped. Without

this substrate potential, our 2D pancake-vortex sys-

tem would melt at T

. The substrate potential sta-

bilizes the crystal and pushes the melting tempera-

ture to higher values — the 3D crystal turns unsta-

ble when the substrate potential collapses. Given the

long-range nature of the pancake-vortex interaction

one expects that the mean-field type analysis as for-

mulated through the self-consistent substrate model

provides accurateresults for the stabilityrange of the

vortex lattice.Note thatwe ignore herethe reentrance

of the melting line at low magnetic fields.

Theaccuratedeterminationofthestabilityregion

of the pancake-vortex crystal requiresnumerical cal-

culation of the thermal renormalization of the shear

modulus c

(T) and the substratepotential ˛

(T): the

simplest analysis is based on a self-consistent har-

monic approximation (SCHA) with a Hamiltonian



(2)

0˛

(K) ¥

˛ˇ

(K) u

0ˇ

(−K) (12.244)

and requires calculation of the thermally averaged

elastic matrix

˛ˇ

(K, u









1−e

iKR





(12.245)

×@

int



, 0)



n=0

@

int



, nd)



12 Vortex Matter 555

(here, the first term corresponds to the expression

(12.69) while the second accounts for the substrate

potential (12.241)) together with the mean squared

displacement amplitude

u



= T



(2)

[¥

−1

]

˛˛

(K, u



) . (12.246)

After Fourier transformation the thermal average in

(12.246) can be expressed through the Debye–Waller

factor exp(−K



u



/2); the 3D crystal becomes un-

stable when this system no longer exhibits a solution

for u



. However, the proper inclusion of anhar-

monic effects require a more accurate analysis going

beyond the SCHA scheme, e.g., the two-vertex SCHA

which includescubic anharmonicities[294,296].The

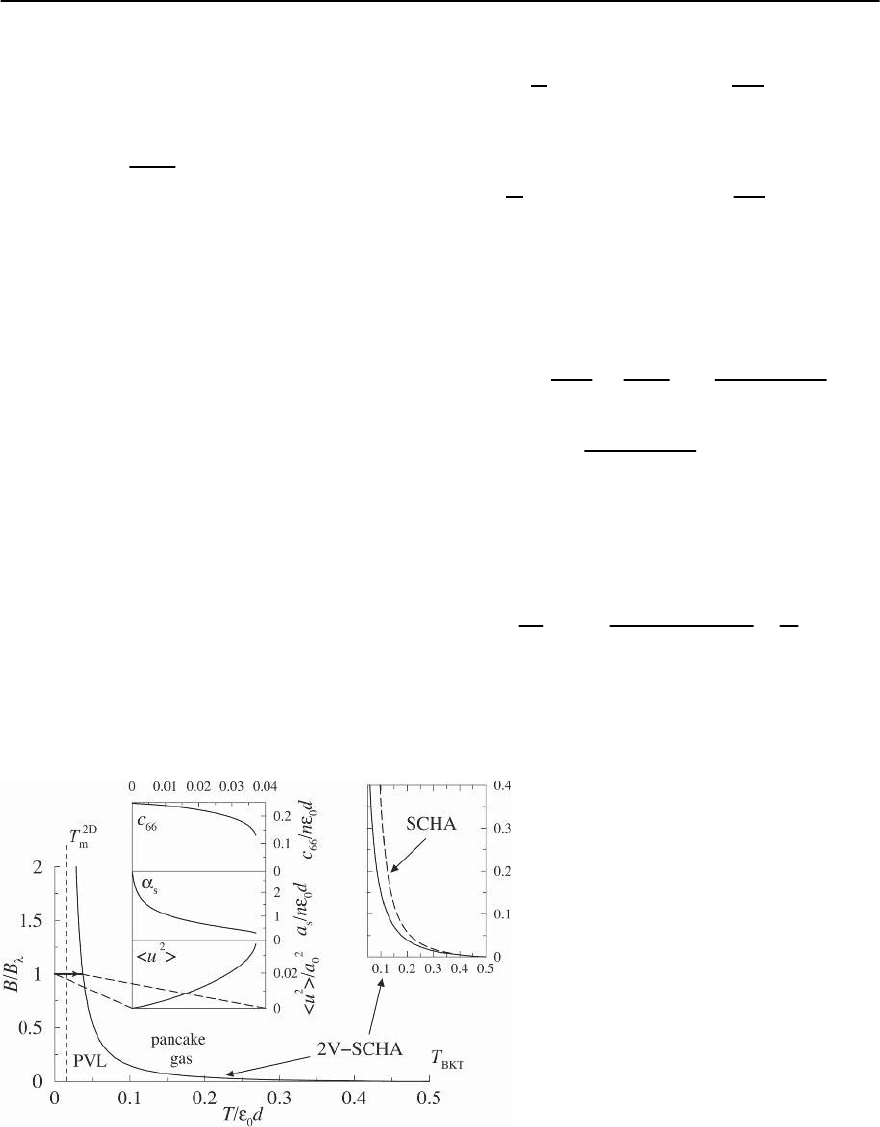
numerical results [294] exhibit a smooth decrease of

(T)and˛

(T) with increasing temperature up to

the instability field B

inst

(T), with reduction factors

∼ 0.5and∼ 0.1 near the collapse, cf. Fig. 12.14.

In order to find the melting line we have to go

one step further: for a first-order transition the low-

temperature phase can be overheated to the upper

spinodal and the instability temperature T

inst

only

provides an upper estimate for the melting temper-

ature T

< T

inst

. The determination of the melting

temperature requires calculation of the free energies

(here at fixed B) of the solid and liquid phases; their

intersection defines T

. The free energy of the solid

can be calculated within a variational scheme: Given

the Hamiltonian H = H

+ H

with







=0

int



, 0) −



int

(R, 0)



(12.247)

and







,n=0

int



, nd)+



int

(R, 0)



(12.248)

the variational free energy F

+ H − H



minimized through the SCHA Hamiltonian H

,cf.

(12.244), and involves the harmonic free energy of

2D ﬂuctuations

=−

NTa



(2)





(/e)T/a

+ ˛



+ln



(/e)T/a

+ ˛



the ground state energy H

− H



=−0.749N"

of a 2D lattice of N log-interacting particles [297],

and the substrate energy

H

− H



−N



2



 =0

exp[−K



u



/2]



(1 + 



)

u





The free energy F

liq

of the pancake-vortex liquid is

calculated from the internal energy U ( )ofa2D

log-interacting system via integration,  F

liq

( )=

Fig. 12.14. Instability line B

inst

for the pancake-

vortex lattice (PVL) in the B–T plane calcu-

lated with the two-vertex-SCHA. The line goes

asymptotically to T

at high fields and ends at

BKT

at zero field. The left inset shows the two-

vertex-SCHA results for the shear modulus c

the substrate strength ˛

, and the ﬂuctuation

width u



with increasing temperature at the

field B = B



.Theright inset is a zoom of the in-

stability line at low fields, and shows the result

(dashed line) of the simple SCHA scheme

556 G. Blatter and V.B. Geshkenbein

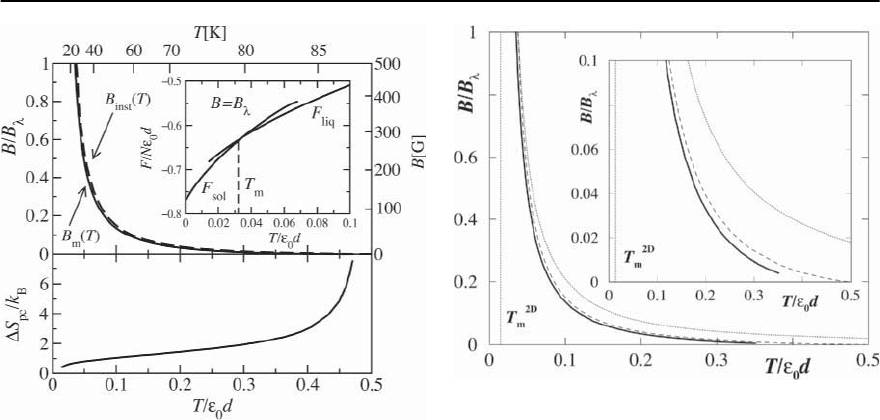
Fig. 12.15. Instability (dashed)andmelting(solid )lines

in an electromagnetically coupled layered superconduc-

tor. The melting line derives from cutting the free en-

ergies of the solid and liquid phases, see inset (data for

B = B



). The lower graph gives the entropy jump per

pancake-vortex S

. Also shown are the real temperature

and field scales assuming (T)=(0)/[1 − (T/T

)

]

1/2

with (0) ≈ 2000 Å,d ≈ 15 Å, and T

≈ 100 K



liq

(







d



U(



), with the internal energy (we

remind that  =2"

d/T)

U( ) ≈ N"

d [−0.751 + 0.880

−0.74

−0.209

−1.7

]

known from numerical simulations [269] and the in-

tegration constant deriving from an exact solution at



=2whereF

liq

(2) = 0.081 N"

d [297] (we assume

that the 2D liquids in neighboring layers have lost

all correlations). The result of this analysis is shown

in Fig. 12.15 and produces a melting line B

(T)very

close to the instability line B

inst

(T)(similarresults

have been found for the stability region of the mag-

netically coupled pancake-vortex lattice within the

framework of density functional theory [298,299]).

The intersection of this melting line with the low-

field reentrant line (12.216) is located at a field value

B/B



≈ 0.005 and a temperature T

d ≈ 0.35 or

1−T

≈ 0.15 (we have used "

d/T

≈ 15; note

that the expression for B



involves the param-

eter /d when expressed through the combination

Fig. 12.16. Comparison of melting (solid) and instability

(dashed) lines obtained within the self-consistent substrate

model with the electromagnetic melting line (dotted)from

a Lindemann analysis with c

=0.065. The discrepancy

between these results at high temperatures is traced back

to the thermal renormalization of elastic coefficients, ac-

counted for in the substrate model but not in the Linde-

mann analysis. The true melting line is expected to reenter

near T

d ≈ 0.35 where our line is terminated

T/"

d and hence the point of reentrance is not uni-

versal; in BiSCCO, the Josephson coupling cannot be

ignored and the point of reentrance is pushed close

to T

The jump in the slope S =−@

F gives the latent

heat TS = U; at high fields the entropy jump

per pancake-vortex takes a value S

≈ 0.4 k

consistent with experiments [42] and simple esti-

mates [300]. The increase of the entropy jump with

temperature follows naturally from the analysis of

the magnetization and entropy jumps in layered su-

perconductors, see (12.268) in Sect. 12.7.6 below.

In Fig. 12.16 we compare the results obtained

within the substrate model with those of the Linde-

mann analysis presentedin Sect.12.7.2above.Choos-

ing a Lindemann number c

=0.065 the results agree

well at low temperatures and high fields,close to the

2D-melting limit (note that a similarly small Lin-

demann number has been found in the discussion

of vortex lattice melting in 2D films, cf. (12.209)).

However, for high temperatures T/"

d → 0.5the

Lindemann result largely overshoots the result from

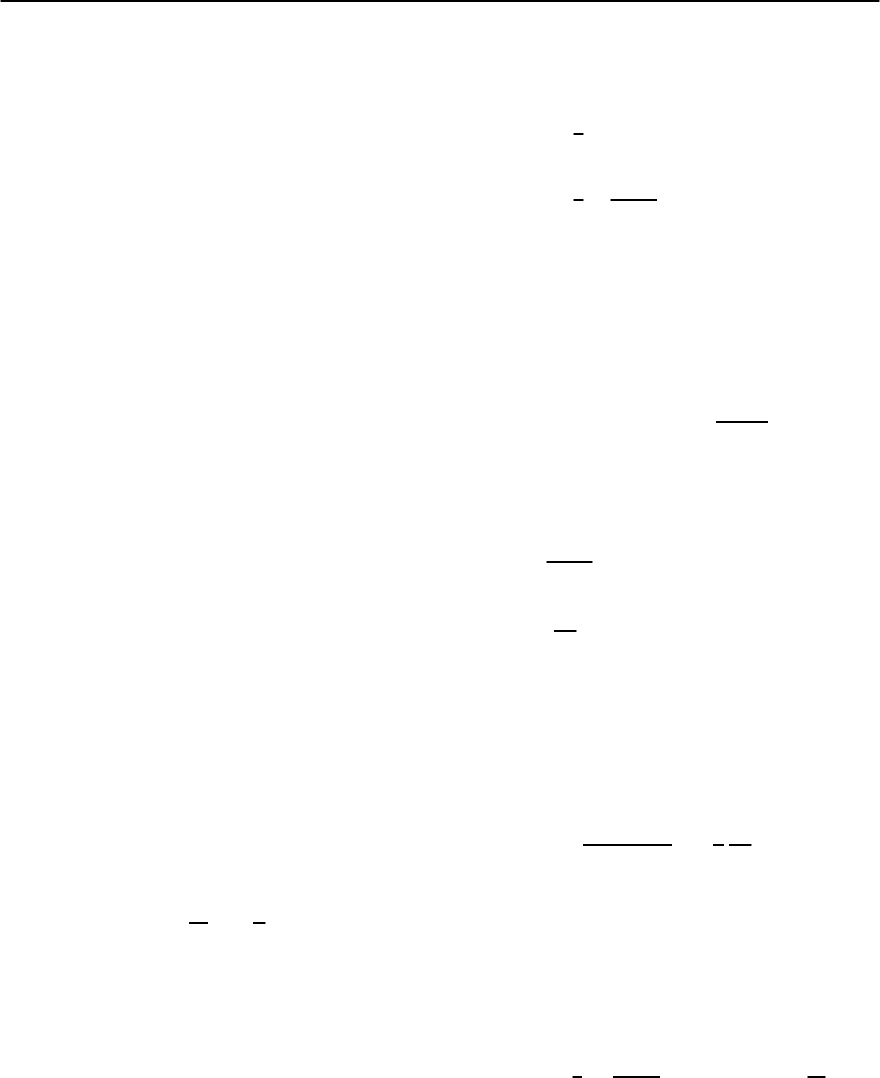
12 Vortex Matter 557

the substrate model (also, the Lindemann result in-

volves the dimensionless temperature T/T

while

the substrate model scales in T/T

BKT

). We can trace

back this discrepancy to the thermal renormaliza-

tion of the elastic constants at high temperatures,

whichis accounted for within the substratemodel,cf.

Fig.12.14,butnot in the Lindemann analysis.Replac-

ing the tilt modulus c

(k) ≈ "

/2a



ˇ in (12.208)

by the renormalized coefficient ("

u



)(1 −

2

/u



) (cf. 12.242) we can properly account for

the thermal softening of the pancake vortex stacks

and the renormalized Lindemann result comes to lie

close to the instability and melting lines of the sub-

strate model.

Defect–Unbinding Transition

The pancake-vortex crystal in an electromagnetically

coupled superconductor exhibits a second phase

transition besides the melting/sublimation transi-

tion discussed above. This second transition is due

to the unbinding of interstitial-vacancy pairs (of the

Kosterlitz–Thouless type) and transforms the low-

temperature, low-field crystal into a 3D defected

crystal at high temperatures or fields [76].The basis

for this transition is given by an interesting screen-

ing effect which exactly (partially) compensates the

logarithmic defect energy in a 2D vortex crystal (3D

pancake-vortex crystal) [301,302].

Consider arigid3Dpancake-vortexlatticein a lay-

ered superconductor and move one pancake-vortex

by the distance

R within the same layer to produce

an interstitial-vacancy defect pair.The excitation en-

ergy associated with this manipulation contains a

self, an interaction, and a core-energy part and reads

i,v

(

R, L)=2"



−ln



+(

+ 

d .

(12.249)

The numericals 

i,v

quantify the core energies of the

interstitial and the vacancy-defect and are of order

0.15–0.2 [303,304] and L denotes the system size.

Next, we let the lattice relax and determine the

screened self-energy of the defect — the interaction

between the defects is screened in the same manner.

We first ignore the electromagnetic coupling to the

pancake vortices in the other layers and take them

into account in a second step later. The interaction

energy of the pancake-vortex configuration reads

int



,



− R



) (12.250)



(2)

n(K)V

(K) n(−K)

(R)=−2"

d ln(R/a

) is the pancake-vortex in-

teraction energy, see

(12.122), and n(K)=





iK·R



denotes the Fourier

transform of the pancake-vortex density), from

which one can derive the dispersive compression

modulus

(K)=n

(K)=

4"

, (12.251)

with n = B/¥

the vortex density. The change in en-

ergy due to the presence of the defect can be written

in the form

ıE

int



(2)

(12.252)



|K ·u(K)|

+in[K · u(K)] V

(K)



While the first term in (12.253) describes the elastic

energy of the relaxed lattice, the second term origi-

nates from the forcethe interstitial exerts on the pan-

cake vortices,E

source





−u



) (we place the

interstitial at the origin). Minimizing (12.253) with

respect to u we obtain the distortion

u(K)=−

inKV

(K)

(K)K

=−

; (12.253)

the displacement u(R)=R/2nR

removes ex-

actly one pancake-vortex from the neighborhood of

the interstitial and thus produces perfect screening

[301]. The log-divergent self-energy in (12.249) then

is compensated by the gain in elastic energy under

the relaxation of the lattice: inserting the solution

(12.253) back into (12.253), we obtain

ıE

int

=−



(2)

(K)=−"

d ln

(12.254)

558 G. Blatter and V.B. Geshkenbein

This perfect screening is spoiled by the interaction of

the pancakevorticesin the layer (n = 0)withthose in

the other layers (n = 0); adding the substrate poten-

tial (12.240) with ˛

=("

d/

)ln(a

/d),cf. (12.148)

where v

≈ ˛

,to the energy (12.253) and mini-

mizing, the displacement field (12.253) is reduced by

the factor 1 + g with [301]

g =

n˛

(K)K

4

≈

. (12.255)

The screening charge is reduced to the fraction

1/(1 + g) and the divergent self-energy in (12.249)

is only partially canceled by the lattice relaxation;

inserting u(K) back into the expression (12.253)

for the change in the interaction energy we obtain

ıE

int

=−"

d ln(L/a

)/(1 + g). The relaxation of the

pancake-vortex lattice then reduces the self-energy

in (12.249) by the factor g/(1 + g). At large fields,

B > H

,where thevortex–vortex interaction is dom-

inated by intraplanar forces, we have g < 1 and a

large downwardrenormalization of the energy of the

defects.When g > 1atsmallfieldsB < H

,theinter-

action between pancake vortices is dominated by the

interlayer forces and the effect of screening is small.

The above analysis extends trivially to the case

of a pancake-vortex vacancy as well as to the in-

teraction between the defects. The energy for an

interstitial-vacancy pancake-vortex pair of extent R

placed into one plane of a decoupled layered su-

perconductor then involves the screened self and

interaction-energies

i,v

(

R, L)=

2g"

1+g

+(



+ 



d . (12.256)

The result (12.256) with its logarithmic interaction

between interstitial-vacancy defect pairs immedi-

ately implies a Berezinskii–Kosterlitz–Thouless tran-

sition [257] where these defects unpair, producing a

crystal with free defects. The field dependent screen-

ing of the interaction pushes this defect-unbinding

transition to low temperatures,

def

(B)=

1+g

, (12.257)

and solving for B we obtain the defect-unbinding line

def

(T)=



4







1−



. (12.258)

Thermal ﬂuctuations soften the substrate poten-

tial and modify the result (12.258): Using (12.242)

with (12.243)we obtain ˛

(T)=(T/

)(1 − 2T/"

d).

The defect-unbindingline then has to be determined

from (12.257) using the renormalized suppression

factor g(T)=(a

/8

)(2T/"

d)(1 − 2T/"

d) for

the superﬂuid density and we obtain the final result

near T

BKT

def

(T)=



8



1−





8



1−T/T

BKT

1−T/T



(12.259)

Here,wehaveusedthat(1−2T/"

d) ≈ [(1 −

T/T

BKT

)/(1 − T/T

)] close to T

. The last factor in

(12.259) replaces the Ginzburg–Landau temperature

dependence in 

−2

∝ 1−T/T

by the temperature

factor1−T/T

BKT

accounting for 2D ﬂuctuationsand

pushes the defect-unbinding line to zero at T

BKT

.Note

that the second factor(1−T/T

)

−1

≈ (1−T

BKT

)

−1

enhances the prefactor in (12.259).

The position of the defect line B

def

(T)shouldbe

compared with the melting line as found in the pre-

vious paragraph. The result of such a comparison

is shown in Fig. 12.17, where we plot the full melt-

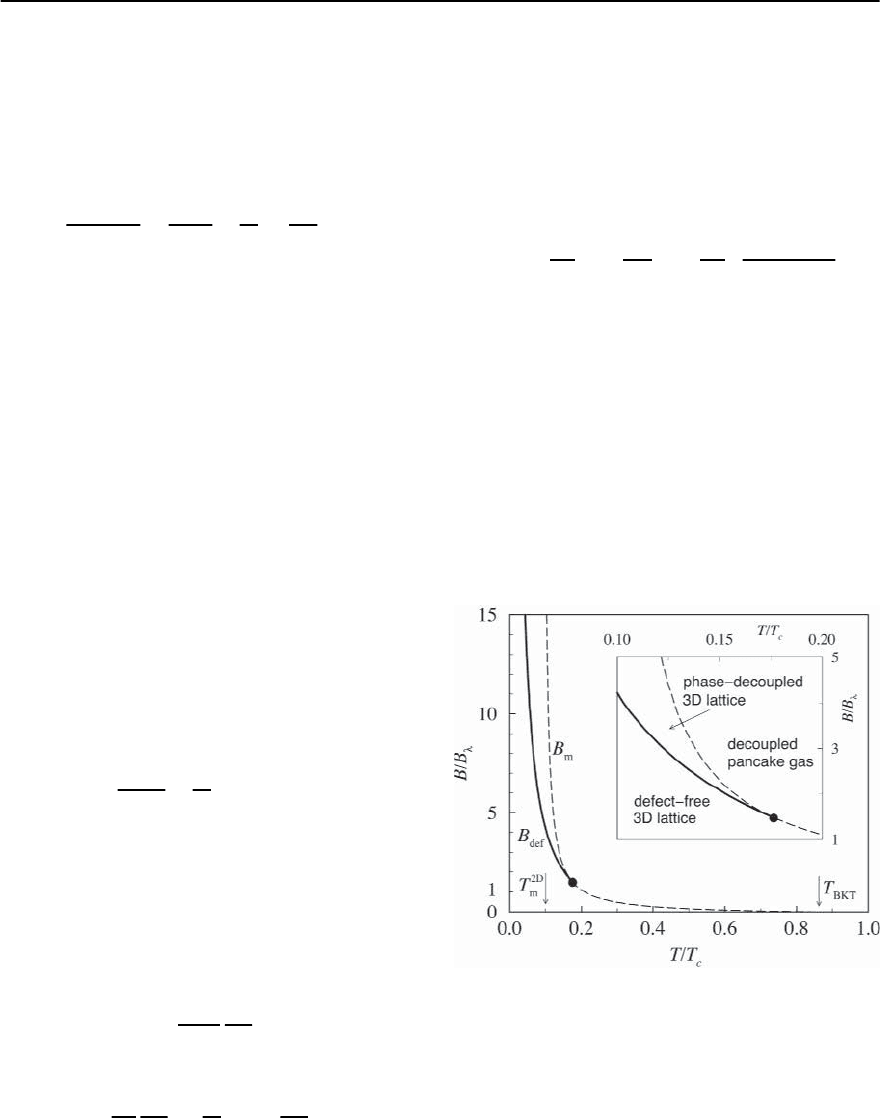
Fig. 12.17. Phase diagram for an electromagnetically cou-

pled layered superconductor. The solid line marks the

defect-unbinding transition B

def

,whichtransformsinto

the decoupling transition B

dec

in the case of a finite weak

Josephson coupling with " < d/.Thedashed line shows

themeltinglineB

calculated within a self-consistent anal-

ysis (with parameters (0) ≈2000 Å,d ≈15Å,T

≈100 K)

12 Vortex Matter 559

ing line B

(T) (dashed) together with the defect-

unbinding line B

def

(T) (solid); we find that the melt-

ing line undercuts the defect-unbinding line, leav-

ing only one (sublimation) transition B

(T)athigh

temperatures,see also Fig. 12.13. Note that the renor-

malized defect line B

def

(T) vanishes rapidly as T ap-

proaches T

BKT

; in principle this allows for a reap-

pearance of the defect line below the melting line as

T → T

BKT

. The analysis of the structure of the phase

diagram near T

BKT

then requires precise knowledge

of the shape of the defect line and of the melting line

including its reentrance; in fact,the reentrance of the

melting line may well preempt the reappearance of

the defect line at high temperatures.At low tempera-

tures, B

def

(T) remains below the melting line, allow-

ing for two transitions separating a defect-free solid,

a defected solid, and a pancake-vortex gas.

The low-temperature defect transition at B

def

≈



d/8T)ln(a

/d) in electromagnetically cou-

pled systems should be compared with the decou-

pling transition B

≈ B



d/T)ln(a

/d) (cf.

(12.231)) in weakly coupled layered superconduc-

tors. Indeed, with a small but finite Josephson cou-

pling present, the lattice defects trigger the decou-

pling of the layers and the defect-unbinding line

def

(T) turns into a decoupling line B

def

(T). For

fields above B

def

(T) the system develops a finite c-

axis resistivity with 

proportional to the density

of free mobile defects n

, see [101]. Close to the un-

binding transition, free defects appear in the solid

with a density n

∼ a

−2

exp[−2



b/(T/T

def

−1)]

(with b a non-universal constant). At higher tem-

peratures the core energy E

core

= "

d determines

∼ exp(−E

core

/T). Such a topological decou-

pling transition based on a quartet-unbinding has

first been proposed by Feigel’man et al. [64] (see

also [74] for a similar supersolid transition).

Whereas the defect-unbinding transition B

def

is the finite-field generalization of the zero-field

vortex-unbinding transition at T

BKT

,thedecoupling

transition B

[73,75] is the finite-field generaliza-

tion of Friedel’s loop transition at T

loop

=8T

BKT

,cf.

Sect. 12.7.1. This pair of transitions is easily derived

from the Lawrence–Doniach model (12.97): for zero

coupling " the individual layer develops a vortex-

unbinding transition at T

BKT

. On the other hand,

restricting ourselves to a pair of (coupled, " > 0)

layers and going over to sum (¥

=(¥

+ ¥

)/2)

and difference (¥

−

= ¥

− ¥

) phase variables we ar-

rive at the Sine–Gordon model with a “roughening”

temperature at 8T

BKT

, independent of the coupling

". Obviously,the zero-field vortex-unbinding transi-

tion at T

BKT

preempts the zero-field loop transition

in the limit of small interlayer coupling. Increasing

the coupling " the transition is shifted upward, cf.

(12.204). The same pair of transitions can be contin-

ued to finitemagnetic fields.The presenceof pancake

vortices then is easily accounted for via the reno-

malization of the superﬂuid density, cf. (12.97) and

(12.154), and we obtain the finite-field versions of

the two zero-field transitions where vortices/defects

unbind and where Josephson loops are created spon-

taneously. Again, in the limit of small coupling the

vortex-induced decoupling transition B

def

is eight

times lower than the “loop” transition at B

,cf.

(12.231).At finite coupling the true transition is ex-

pected at a value between B

def

and B

:comparing

the Josephson energy 

def

with E

= "

d/

,see

(12.97), within the coherence area 

def

≈ n

−1

with

the temperature we estimate the upward shift of the

decoupling transition due to the Josephson interac-

tion

(B) ≈

core

[

core

d)(B/B



)

]

. (12.260)

While the result (12.258) is valid at low fields, the

steep upward shift described by (12.260) becomes

effective when g ≈ H

/B < / ln(d/"), with

 = E

core

d the numerical quantifying the core

energy of the defects (see [303,304] where numeri-

cal values  ≈ 0.15 − 0.2 are reported). The quan-

titative condition for the applicability of the result

(12.258) thus depends both on the anisotropy pa-

rameter " as well as on the defect core-energy E

core

At higher fields B > (8/)ln(d/")H

the decou-

pling line crosses over into the “loop” transition at

as given by (12.231)[73,75];an accurate descrip-

tion of the crossover between the defect and “loop”-

transitions requires a generalization of the analysis

in [82] to finite fields.

The pair of transitions discussed above is not

unique to the vortex system discussed here — it ap-

pears in the context of the XY-model (with coupling