Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

570 G. Blatter and V.B. Geshkenbein

length scale. Within weak collective pinning theory

the sublinear growth of E

(V)

1/2

goes over into

a linear law when the displacement field u increases

beyond the characteristic size r

of ﬂuctuations in

the pinning potential E

.EachvolumeofsizeV

then is pinned independently with a pinning energy

= E

)

1/2

. As the pinning energy grows lin-

early with volume beyond V

we obtaina proper pin-

ning force density

∼



imp

(/a

)



1/2

. (12.287)

Balancing this pinning force density against the

Lorentz forcedensity jB/c wearrive at a finitecritical

current density j

∼ cF

/B. Note the opposite scal-

ing with V

of the pinning energy U

∝

√

and the

critical current density j

∝ 1/

√

, a characteristic

feature of the weak collective pinning theory.

The remaining task is the determination of the

collective pinning volume V

;itscalculationiscom-

plicated by the dispersion and anisotropy of the vor-

texlattice andwill be carried outin Sect.12.9.Assum-

ing an isotropic non-dispersivemodel system withan

elasticity C,the comparison of elastic (C(r

)

and pinning (U

) energies provides the collective

pinning length (we choose d =3)

∼

imp

. (12.288)

Combining (12.287) and (12.288) we obtain the crit-

ical current density

∼ j

imp

]

imp

, (12.289)

where we have reexpressed the bulk elasticity C =

through the corresponding line elasticity "

12.8.3 Weak versus Strong Pinning

It is instructive to compare the weak and strong

pinning schemes and their dependence on dimen-

sionality, particularly in the limit of a small defect

density. We analyze strong pinning and the Labusch

criterion (12.285) using a simple (isotropic) Ansatz

G(k)=1/Ck

for the elastic response function

(G(k)=1/"

in the 1D problem, G(k)=a

ina2Dfilmofthicknessd,andG(k)=a

for

the 3D situation).We will find that in one and two di-

mensions the effective elastic coefficient

C drops to

zero as the integral in (12.283) diverges and we have

to modify our analysis. The original Labusch crite-

rion (12.285) identifying individual pinning centers

as strong ones is applicable in 3D only where the

integral in (12.283) converges.

One Dimension: Single Vortex Pinning

In 1D, individual pins are always strong as the effec-

tiveelasticcoefficient

C vanishes due to the diverging

integral in (12.283). At the same time, the deforma-

tion of the line due to the action of these pinning

centers is large and we cannot ignore their mutual

competition. The collective pinning analysis in 1D

then provides us with the collective pinning length

∼ ("

imp

)

1/3

and a critical current density

∼ j



imp



imp



2/3

. (12.290)

This result is valid as long as many pins compete

within the volume 

; the condition n

imp



> 1

puts a lower limit ¯n

∼ f

imp



< n

imp

on the

defect density, where the critical current density as-

sumes the value

∼ j

imp

)

For small densities n

imp

< ¯n

each pin acts in-

dividually and we can determine j

from the force

balance (¥

/c)j

lu ∼ e

∼ f

imp

u,withu ∼ t



the

displacement directed along the force acting on the

vortex.The length l between two subsequent pins fix-

ing the vortex derives from an analysis of the pinned

vortex geometry, see Fig. 12.24: Integrating the force

equation

= f (z) (12.291)

(here, f (z) denotes the force per unit length acting

on the line) over one pinning center we find the an-

gle = @

u ∼ f

imp

distortingthe vortex line at the

location of the defect; alternatively,we cut the diverg-

ing integral in (12.283) on the scale l,

C ∼ "

/l,and

the relation u ∼ f

imp

C provides us with the defor-

mation angle  ∼ u/l ∼ f

imp

. A vortex segment

12 Vortex Matter 571

Fig. 12.24. Strong pinning geometry for a vortex line. The

deformed vortex probes the volume l

 of width  in the

direction transverse to the line and the motion

of length l deformed by the angle  in the direction

of the driving force encounters l

n

imp

defects (as-

suming a transverse trapping length t

⊥

∼ )andwe

find the distance l when this number is unity, hence

l ∼



imp

f

imp

. (12.292)

Combining this result with the expression for the

critical current density we find

∼ j



imp



imp



1/2

. (12.293)

At the crossover density ¯n

∼ f

imp



the criti-

cal current density matches up with the weak pin-

ning result,

∼ j

imp

)

. Also, the displacement

u ∼ lf

imp

∼ 



imp

)/(n

imp



)isoforder

at the strong to collective-pinning crossover density

¯n

and hence smoothly matches the displacement

field relevant in the collective pinning scenario. Note

that the collective pinning expression (12.290) dom-

inates over the strong pinning expression (12.293) at

large densities n

imp

> ¯n

Two Dimensions: Pinning in a Film

Again, individual pinning centers are strong, how-

ever, the effective elastic constant

C diverges merely

logarithmically,

−1

∼ (a

d)ln(L/ ). The cut-

off length L is given by the distance to the

next effective pin as determined from the condi-

tion n

imp

trap

)dL

∼ 1, L ∼ a



imp



⊥

d,cf.

(12.280). Assuming a transverse trapping length

⊥

∼  we solve for the longitudinal displacement

u ∼ t



∼ f

imp

C and find u ∼ a

imp

d) ×

ln("

imp



). Given the trapping area S

trap

easily find the mean force density F

= n

imp

f

∼

imp

f

imp

]ln("

imp



) and the correspond-

ing critical current density

∼ j

imp



imp



. (12.294)

This result is valid for large impurity forces

imp

and at small enough pinning densities

imp

where neighboring pinning centers do not

compete. The competition between neighboring

centers appears when the displacement u ∼

imp

d)ln("

imp



) drops below the

width  of the individual pinning centers — in this

situation,the competing elastic forces inhibit the op-

timal use of all the pins. Hence pinning turns collec-

tive below the critical force

Lab

∼ "

d

ln(a

imp

d

)

; (12.295)

the same expression derives from the Labusch crite-

rion (12.285).Note that this “Labusch force”involves

the distance to the next pin as a cutoff in the log-

arithm, in contrast to the original concept charac-

terizing individual centers. Below f

Lab

the collective

pinning scheme provides the results

∼



imp

, F

∼ n

imp



imp

∼ j

imp



imp

; (12.296)

572 G. Blatter and V.B. Geshkenbein

at crossover, the collective pinning volume contains

imp



∼ ln

/ n

imp

d

) > 1activepin-

ning centers. Comparing (12.294) and (12.296) we

note that the strong pinning result is logarithmically

larger.

Three Dimensions: Bulk Pinning

The Labusch criterion (12.285) offering a distinc-

tion between weak and strong individual pinning

centers becomes applicable in 3D, where the inte-

gral in (12.283) converges and the elastic coefficient

C remains finite,

C ∼ "

. According to (12.285)

an individual pinning center becomes strong when

imp

> f

Lab

≡ (/a

We begin with the analysis of the weak collective

pinning situation assuming f

imp

< f

Lab

(where nec-

essary, we code quantities in this regime with a su-

perscript “

”) and find the following results for the

3D vortex system

∼

imp



imp



, F

∼ n

imp



imp

∼ j

imp

a

)

imp

∼ j

imp



)

imp

Lab

(12.297)

These results are valid as long as many (competing)

pins are active in the volume L

imp

(

> 1.

For densities larger than ¯n

∼ (f

Lab

imp

)



)

−1

each pin would act individually (note that pinning

is collective at low densities n

imp

< ¯n

in 3D, but

at high densities n

imp

> ¯n

in 1D). However, before

reaching the critical density ¯n

the collective pin-

ning length L

drops below the distance a

between

the vortex lines: the condition L

∼ a

provides us

with the crossover density ¯n

∼ (f

Lab

imp

)



¯n

where 3D weak collective pinning smoothly

crosses over into the 1D weak collective pinning re-

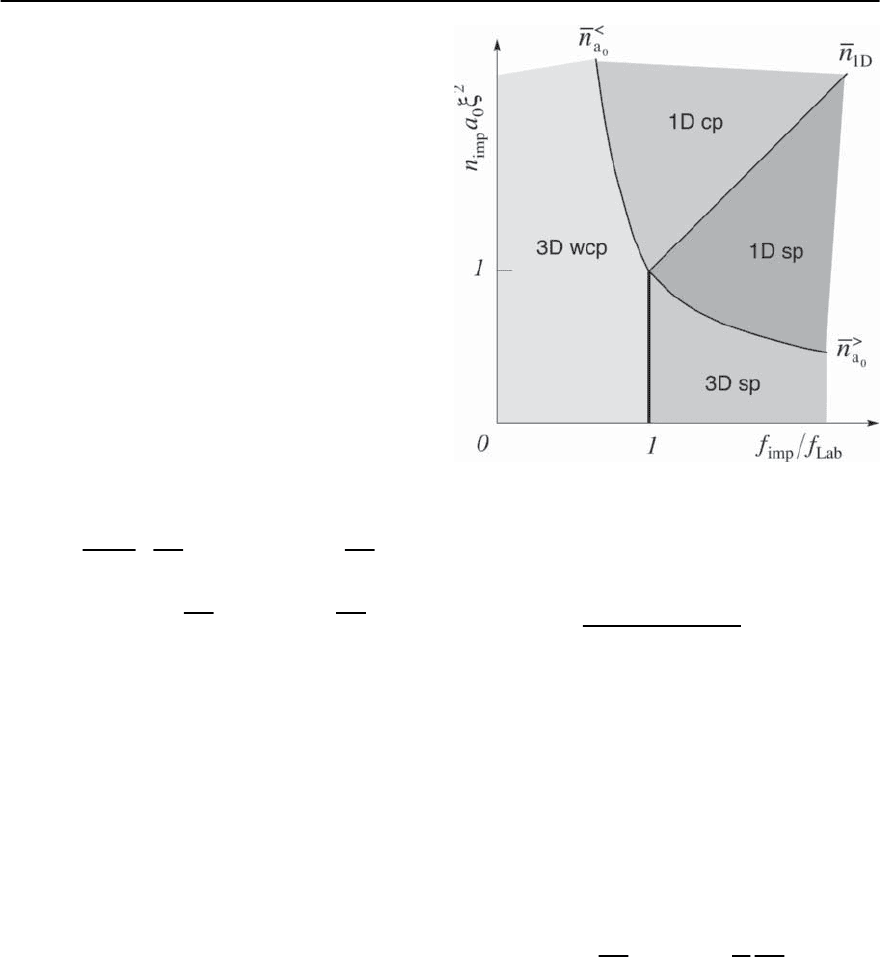
sult (12.290), see Fig. 12.25.

Turning to strong pinning f

imp

> f

Lab

(coded

with a superscript “

”) we first consider high den-

sities; as the Labusch criterion is not effective in

1D the system remains collectively pinned as long

as n

imp

> ¯n

and then smoothly crosses over to

the 1D strong pinning as n

imp

is decreased below

Fig. 12.25. Pinning diagram delineating various pinning

regimes involving collective versus individual pinning and

1D-line versus 3D-bulk pinning: 3D wcp – bulk weak col-

lective pinning, 1D cp – collective line pinning, 1D sp –

strong line pinning, 3D sp – bulk strong pinning

¯n

. With decreasing density n

imp

the pinning dis-

tance l ∼ a



lab

imp

)/n

imp



, cf. (12.292), in-

creases beyond a

as n

imp

decreases below ¯n

∼

Lab

imp

)/a



and the system enters the 3D strong

pinning regime, see Fig. 12.25. The calculation of the

mean pinning force density F

∼ n

imp

f

 pro-

ceeds along the lines discussed above in Sect. 12.8.1

and involves the trapping area S

trap

∼ t



(we as-

sume a transverse trapping length t

⊥

∼ )with



∼ u ∼ f

imp

C determined by the effective elas-

tic constant

C; we obtain a mean pinning force den-

sity F

∼ n

imp

(/a

imp

and a critical current

density

∼ j

imp



imp

∼ j

imp



imp

Lab

. (12.298)

The bulk strong pinning result (12.298) smoothly

transforms into the 1D expression (12.293) at ¯n

where l ∼ a

. On the contrary, the strong pinning

expression (12.298) apparently does not match up

with the bulk weak collective pinning result (12.297)

upon crossing from strong centers f

imp

> f

Lab

12 Vortex Matter 573

weak impurities with f

imp

< f

Lab

(here, we concen-

trate on low impurity densities n

imp

< 1/a



,cf.

Fig.12.25).However,we have to keep in mind that our

rough derivationof thestrongpinning result (12.298)

breaks down on approaching the critical force f

Lab

Indeed,since the displacement field u(r) turns single

valued below f

Lab

,strong pinning vanishes altogether

(with a power [f

imp

− f

Lab

]

) and pinning survives

only in the form of weak collective pinning due to

ﬂuctuations in the impurity density. Within the ap-

proximative scheme adopted here the sharp rise of

the critical current density at f

imp

> f

Lab

is encoded

in a jump j

wcp

∼ 1/n

imp



> 1.

The above discussion sheds more light on the con-

cept of pinning in general. Starting from the rigid

limit we understand that such a stiff lattice cannot

be pinned. Going over to a finite but still large elas-

ticity (such that f

imp

< f

Lab

) the weak deformations

produced by individual pins do not allow individual

pins to hold the lattice; indeed, following the discus-

sion in Sect. 12.8.1 the averaging of individual pin-

ning forces produces a null result,cf. (12.280).In this

situation pinning appears only as a consequence of

ﬂuctuationsin the pinning forces,i.e.,thesecondmo-

ment rather than the first moment in the forcedistri-

bution function establishes a finite average pinning

force density. Reducing the elasticity, the individual

centers turn into strong ones when f

Lab

drops below

imp

. These strong pinning centers now start to pin

the lattice individually and strong pinning, linear in

the defect density n

imp

, outperforms collective pin-

ning; hence, the first moment of the force distribu-

tion function takes over the leading role in the pin-

ning process.This crossover between weak collective

andstrongpinningcaninfactberealizedinanexper-

iment: increasing the magnetic field to approach the

upper critical field H

leads to a marked softening

of the elastic moduli,cf.thediscussion in Sect.12.4.1.

The reduction in the elastic moduli entails a decrease

of the Labusch force f

Lab

and triggers the crossover

from weak to strong pinning, producing the famous

peak effect in the critical current density [10].

12.8.4 Vortex Creep

Thermal ﬂuctuations affect the vortex system in

many respects; while their implications on the ther-

modynamic equilibrium state have been discussed in

Sect. 12.7 above, thermal ﬂuctuations interfere with

pinning in two ways: the rapid thermal motion of

the ﬂux lines within their pinning valleys produces

a smearing of the energy landscape and leads to a

downward renormalization of the pinning strength,

see Sect. 12.9.5 below. On the other hand, the cur-

rent carrying state of a hard type II superconduc-

tor as given by the Bean state is only metastable

and thus bound to decay: large thermal ﬂuctuations

help the ﬂux lines to overcome their pinning barri-

ers and move to the next favorable pinning valley

where they are retrapped. This leads to a thermally

activated motion of vortices commonly known as

creep [14, 334] (see Kramers’ pioneering work on

the problem of thermally activated processes and

metastability [335] and [336] for a review on this

topic).

The basic equations determining the decay of the

current density j are given by Maxwell’s equation,

B =−c @

E, where we use a geometrical arrange-

ment with the field B ˆz and the current density j

and electric field E = B ∧ v/c pointing along the y-

axis. The velocity of the vortices is parallel to the

Lorentz force, v =(v, 0, 0). Inserting the expres-

sion for the electric field into Faraday’s law we ob-

tain the equation of continuity for the vortex lines,

B =−@

(vB), and expressing j through B using

Amp`ere’s law we arrive at the dynamic equation for

the current density j,

j =

4





. (12.299)

Here, the most important factor is the velocity v of

the vortices which is due to thermal activation over

the pinning barrier U(j),

v = v

exp[−U (j)/T] , v

∼ j

B/c , (12.300)

leading to a non-linear diffusion equation [337] for

the current density j

j ≈ −



exp



−

U(j)



. (12.301)

574 G. Blatter and V.B. Geshkenbein

The relaxation time  ∼ (H

/H)

depends

on the sample dimension w and hence is a macro-

scopic rather than a microscopic time scale [38,337].

The above equation can be solved with logarithmic

accuracy [338] and we obtain

U(j)=T ln





, (12.302)

with t

= T/j

U|. Using (12.302) the time evolu-

tion of the screening current density j(t)isobtained

by simple inversion.

The important quantity which we need to know

is the activation energy U(j), in particular, its func-

tional dependence on the current density j.Theen-

ergy scale for the pinning barrier U is determined by

the pinning energy U

. The dependence of U on the

transportcurrentdensity j is dueto theLorentzforce;

as j approaches j

from below the barriers vanish,

U(j → j

) ≈ U



1−



, (12.303)

and the vortices depin. The numerical value of the

exponent ˛ depends on the physical situation: e.g.,

the activation of a particle over a smooth barrier in-

volves the exponent ˛ =3/2,while creep of an elastic

string trapped along its length in a smooth potential

well is described by the exponent ˛ =5/4(thiscor-

responds to the situation of intrinsic pinning with

vortex lines arranged parallel to the ab planes or to

vortex pinning by columnar tracks,see Sect.12.10.1).

In his phenomenological discussion, Anderson [14]

used the value ˛ = 1 and this value is also found in

an analysis of pinning by random point-like defects

within the framework of weak collective pinning the-

ory [339].Combiningthe dynamics (12.302)with the

disappearance of barriers near j

we obtain the fa-

mous logarithmic time decay of the (diamagnetic)

current (we choose ˛ = 1 here),

j(t)=j



1−







. (12.304)

The temporal decay of the transport current is thus

determined by the ratio T/U

which can be found ex-

perimentally by measuring the relaxation of the dia-

magnetic moment of a sample in the critical state;

typical experimental results for the activation en-

ergy U

in high-T

superconductors measured at

low temperatures are in the range U

∼ 100–1000

K [44–46,340,341]. Since pinning in these materials

is usually weak,such measurements of the activation

energy U

provide a useful test of the validityof weak

collective pinning theory.

So far we have concentrated on the case where j

is near to its critical value j

, a restriction reasonably

justified in conventional hard type II superconduc-

tors with typical decay coefficients T/U

of the or-

der of 10

−3

[342,343]. In the oxide superconductors

pinning is weak and the corresponding decay coeffi-

cients are much larger, reaching values of order 5%

at temperatures T ≈ 20 K [46,344].These large loga-

rithmic decayratesarea resultof variousfactorssuch

as the high temperatures available in an experiment

and the small pinning energies U

(small coherence

length ,large anisotropy). Combining the large de-

cay coefficients with a typical logarithmic time factor

ln(t/t

) of the order of 20 we conclude that the cur-

rent density j can decay to a (small) fraction of the

critical current density j

during an experiment.The

determination of the critical current density in the

oxides then is always affected by the presence of “gi-

ant”creep [44–46]and the condition j

−j  j

is not

valid in general.

From a scientific point of view the case j  j

and in particular the limit j → 0 is very interesting:

If we wish to probe the thermodynamic state of the

vortex structure we should perturb the system only

infinitesimally and record its response. For a truly

superconducting state we expect to observe a van-

ishing resistivity  in the limit j → 0or,inasome-

what different language, to see a sublinear “glassy”

response of the vortex structure.Assumingweak col-

lective pinning, we will see below (cf. 12.9.4) that the

barriersU(j) against creep diverge algebraically with

vanishing current density j,

U(j) ≈ U







, (12.305)

implying a strongly subohmic current-voltage char-

acteristic of the form

V ∝ exp



−









. (12.306)

12 Vortex Matter 575

The divergence of the creep barriers described

through the collective creep theory (cf. Sect. 12.9.4)

is based on the elastic properties of the vortex sys-

tem. If these elastic properties are lost, the barriers

are expected to saturate at a value U

(the so-called

plastic barrier), resulting in thermally activated ﬂux

ﬂow response (TAFF [56]). This scenario is realized

in a vortex liquid phase where the shear modulus

collapses, resulting in a plastic barrier U

∼ ""

and an ohmic current-voltage characteristic.

The aboveideasare amenableto experimental ver-

ification if the sample can be preparedin a statechar-

acterized by a small transport current ﬂow (Maley

plot) [17,345]: warming a sample in the criticalstate,

the decay rate of the shielding current can be in-

creased by several orders of magnitude such that the

current density j drops far below its critical value j

within experimentally accessible time scales, allow-

ing to probe the small current regime j  j

12.9 Uncorrelated Disorder: Collective

Pinning and Creep

The theory of weak collective pinning produced by

an uncorrelated disorder potential due to a high den-

sity of weak point-like defects has been studied in

great detail [10,150]; below we first concentrate on

weak collective pinning of vortex lines and vortex

bundles and then proceed with a discussion of col-

lective creep, both thermal and quantum. Thermal

ﬂuctuations not only produce vortex motion; they

also smear the pinning potential and thus lead to

a downward renormalization of the critical current

density.We end this section with a discussion of pin-

ning in layered superconductors where the layered

structure introduces elements of strong pinning.

The classic example of weak collective pinning is

based on a short-ranged (uncorrelated) disorder po-

tential as produced by point-like defects. On a tech-

nical level such a pinning landscape is introduced

into the Ginzburg–Landau model via spatial varia-

tion in the GL coefficient ˛(r) describing changes

in the (local) transition temperature T

, and/or by

spatial variation of the effective mass m



(r)de-

scribing changes in the mean free path l.Forthe

generic case of weak point-like pins the disorder

landscape is usually characterized by a Gaussian dis-

tribution, e.g., ˛(r)=˛

+ ı˛(r)withı˛ =0

and ı˛(r)ı˛(r



) = 

ı(r − r



), and similarly

for m



(r)=m

0

+ ım



(r)withım



 =0and

ım



(r)ım





) = 

m



ı(r −r



).The pinning en-

ergy acting on a vortex line then is obtained by a

convolution of the disorder potential U

(r) and the

form factor p(R) of the vortex line [we concentrate

on theisotropiccase here;theanisotropic situation is

handled with the help of anisotropic scaling theory,

see (12.170)],



(u, z)=



(r) p(R − u) , (12.307)

with

(r)=

⎧

⎪

⎨

⎪

⎩

ı˛(r)|¦

ım(r)

|¦

p(R)=

1−|¦

(R)|

, ıT

−pins,



|∇¦

(R)|

, ıl −pins;

a convenient choice for the (normalized) vortex so-

lution is [123,124] ¦

≈ [R/(R

+2

)

1/2

]exp(i' ).

The pinning energy correlator

U

(r)U



) = ı(r − r



) (12.308)

has a weight ([ ] = energy

/volume)

 =

⎧

⎪

⎨

⎪

⎩





4



, ıT

− pinning ,





4



, ıl − pinning .

(12.309)

The correlator for the vortex pinning energy takes

the form



(u, z)



, z



)

= ×



R d



U

(r)U



)p(R − u)p(R



− u



)

= ı(z − z



)K(|u − u



|) , (12.310)

with the disorder correlator

K(u)=



Rp(R − u)p(R) . (12.311)

576 G. Blatter and V.B. Geshkenbein

The detailed shape of the correlator K(u) depends

on the vortex form factor p(R); making use of the

above vortex solution ¦

we find a sharply peaked

function of width u ∼  and height K(0) ∼ 

(we find K(0) = 2

for ıT

-pinning and K(0) =

(12/15)

for ıl-pinning). The slow (algebraic)

decay of the vortex currents at distances R <  pro-

duces a correlator with slowly decaying tails, K(u →

∞) ∼  (

)ln(u/ ).Quiteoften,thesimple form

function p(R)=exp(−R

/2

)isused,producing

a Gaussian correlator K(u)=

exp(−u

/4

)

[346,347].

In calculating the pinning energy correlator of the

vortex lattice the structure factor has to be replaced

by that of the lattice which occupies only a fraction



of the volume, cf. (12.286).For small displace-

ments u < a

the disorder landscape is short-scale

correlated with

E

(u, r)E



, r



) = ı(r − r



)

K(|u − u



|) .

(12.312)

For displacements u > a

the vortex lattice probes

the same disorder landscape and the correlator K(u)

has to be replaced by a periodic one [19–21].

The generic abstract problem we are confronted

with in this section is that of a d-dimensional elas-

tic manifold moving in n transverse dimensions and

subject to a disorder potential; the free energy of this

object takes the form

F =





(∇u)

+ E

(u, r)



, (12.313)

with the correlator

E

(u, r)E



, r



) = ı

(r − r



)K(|u − u



|) .

(12.314)

For a single vortex line d + n =1+2,r → z,

C → "

,andE

→ 

with a correlator (12.310),

K(u)=K(u); for the vortex lattice d + n =3+2,

the elastic part (C/2)(∇u)

of the free energy has

to be replaced by the dispersive expression (12.95)

and the disorder correlator is given by (12.312),

K(u)=K(u)/a

12.9.1 Dirty Elastic Manifolds

To acquaint ourselves with the dirty elastic manifold

problem we brieﬂy outline a few pertinent results.

The interesting behavior of this system results from

the competition between elasticity, thermal ﬂuctua-

tions, and quenched disorder. Let us study the be-

havior of the manifold on the scale |r| = L and first

ignore the disorder energy E

;thenthe competition

between the elastic energy ∼ Cu

d−2

and the tem-

perature T results in distortions[u(L)−u (0)]



1/2

≡

u

(L)

1/2

∼

√

T/CL



with the thermal exponent



2−d

, (12.315)

independent of the number of transverse dimen-

sions n. An elastic string (d = 1) then exhibits ther-

mal wandering u

(L)

∝ TL, while the distortions

grow only logarithmically for an elastic membrane,

u

(L)

∝ T ln L for d =2.Abovetwodimensions

elasticity wins over thermal ﬂuctuations and the

manifold remains undistorted at large scales. As an

illustration consider a scattering experiment probing

the locations of atoms in a crystal: the long-range or-

der in the three-dimensional crystal produces sharp

ı−function peaks which are only reduced in magni-

tude by thermal ﬂuctuations (via the Debye–Waller

factor). On the other hand, in a two-dimensional

crystal thermal ﬂuctuations turn the reﬂections into

algebraic peaks, cf. Sect. 12.7.4.

Next, let us ignore thermal ﬂuctuations and in-

vestigate the effect of quenched disorder. Assuming

weak disorder we can study its effect in perturbation

theory [18] using the Green’s function G ∼ 1/Ck

of the elastic free energy (the “free” problem). Then

u(k)=−G(k)∇

(u, k) and we find (to lowest or-

der in u) a disorder-induced roughening

u

(L)

dis

∼ K



(0)



[1 − cos(k ·r)]

(Ck

)

(12.316)

For d ≤ 4 the integral in (12.316) is determined

by the lower cutoff ∼ 1/L and we obtain the result

u

(L)

dis

∼ [K



(0)/C

4−d

. Hence disorder is rele-

vant in dimensions d < 4 and marginally relevant in

d =4withu

(L)

dis

∼ [K



(0)/C

]lnL.Withinper-

turbation theory the effect of the disorder potential

12 Vortex Matter 577

is encoded in the force–forcecorrelator K



evaluated

at u = 0. The above perturbative approach breaks

down in low dimensions d ≤ 2 as the integral in

(12.316) diverges at small k; however, the result



4−d

(12.317)

for the wandering exponent remains valid, as scal-

ing arguments show [10]: balancing the elastic en-

ergy ∼ Cu

d−2

against the disorder energy [K



(0)

]

1/2

we recover the Larkin exponent 

indepen-

dent of the number of transverse dimensions n (this

scaling result is confirmed by other, more rigorous,

approaches [348,349]).

Perturbation theory also breaks down at large

distances L > L

when u

(L)

1/2

dis

> r

increases

beyond the scale r

defined by the disorder po-

tential E

; the condition u

)

dis

= r

defines

the crossover length L

=(r



(0))

1/(4−d)

[10].

While the manifold probes only one pinning val-

ley at small scales L < L

, the availability of many

(metastable) minima allows for further optimiza-

tion of the manifold’s state at large scales L > L

[350,351].The determination of the large-scale wan-

dering exponent 

d,n

is a difficult problem in the

statistical physics of disordered systems [111,112];

the simplest approach producing an acceptable esti-

mate is based on simple Flory- [352]/Imry-Ma [353]

type scaling arguments. The crucial element in such

a scaling estimate is to find an appropriate Ansatz

for the disorder energy. At short distances, where

only one pinning valley is relevant, the potential

can be expanded, E

(u) ∼ −F

· u, resulting in

the above estimate E

∼[K



(0)u

]. On large

distances we cannot expand any longer and have

to estimate the disorder energy E

 directly from

the potential E

. Assuming a disorder landscape

with Gaussian disorder described by the correlator

(12.314) we adopt the asymptotic power-law Ansatz

K(u) ∼ u

−ˇ

;thevalueˇ = n describes a short-

range correlatedrandom potential (K(u) ∼ ı

(u)),

forˇ = −2 we recoverthe Larkin Ansatz for a random

force field, and ˇ =−n corresponds to the (long-

ranged) random-field situation [354]. This scaling

Ansatz for the disorder correlator then produces a

pinning energy scaling as E

[V = L

, u(L)]

1/2

∼

(L

−ˇ

)

1/2

∼ 

1/2

(d−ˇ)/2

,andcomparingtothe

elastic energy C(u/L)

∼ CL

d−2+2

we obtain the

Flory type result



d,n

4−d

4+ˇ

. (12.318)

Again, we find that disorder disrupts the manifold

in dimensions d < 4 [18] and choosing ˇ =−2we

recover the Larkin exponent 

=(4−d)/2. The

“Flory” expression is believed to provide the exact

result [354] for the random-field problem (ˇ =−n)

where a mean-field analysis is valid.Also, a more so-

phisticated approach based on the introduction of

replicas and use of a variational harmonic Ansatz

for the free energy confirms the Flory type for-

mula (12.318) when an appropriate replicasymmetry

breaking scheme is applied [355]. On the other hand,

it is clear that the “Flory”result is only approximate

for the short-range case ˇ = n as it misses to repro-

duce the exact result 

1,1

=2/3 known for the di-

rected polymer problem (d =1)withonetransverse

dimension (n = 1) [356]. The functional renormal-

ization group (FRG) theory [357] allows to elaborate

ontheprobleminamorecontrolledmanner.Within

an  =4−d expansion the 1-loop renormalization

group equation for the (scale dependent) disorder

correlator K

(u) involves the usualscaling terms plus

quadratic corrections arising from integration over

short scale disorder [357,358],

(u)=( −4)K

(u)+u



(u) (12.319)

+ I[K



(u)K



(u)/2−K



(u)K



(0)] ,

with I = S

d−1



d−4

/(2)

, l =lnR,and a

short scale cutoff; S

d−1

is the surface area of the

unit sphere in d dimensions and we have introduced

the notation K

..

≡ @



.. K

to denote derivatives

(the last term in (12.320) can be rewritten in terms

of derivatives with respect to u and takes the form

I[K



(u)/2−K



(u)K



(0) + (n −1)K



(u)/2u

−(n −

1)K



(u)K



(0)/u]). A straightforward numerical so-

lution of the fixed-point equation provides the results



d,1

≈ 0.2083  [357] and 

d,2

≈ 0.1766  [359]. An

alternativeanalytic scheme to determine the wander-

ing exponent  puts the emphasis on the asymptotic

behavior of the fixed-point function [360]: looking

578 G. Blatter and V.B. Geshkenbein

for a fixed-point solution with an algebraic asymp-

totic K

∗

∝ u

−ˇ

∗

, the scaling terms define the expo-

nent  = /(4+ˇ

∗

) andthusreproducethe“Flory”re-

sult (12.318) with ˇ = ˇ

∗

.Inaddition,thefull1-loop

fixed-point equation also allows for a short-ranged

fixed-point function with a rapidly decaying Gaus-

sian form, K

∗

(u) ∝ u

4+n−/

exp[−u

/2] [357].

The following general picture capturing the behav-

ior of both long-range random-field (ˇ < 0) and

short-range random-bond (ˇ > 0) problems then

has been proposed [360]: For large negative ˇ the

FRG ﬂow does not modify the asymptotic behavior

of the correlator,ˇ

∗

= ˇ and the“Flory” result holds.

Increasing ˇ from below (i.e., decreasing the corre-

lator’s range) we should stop the further increase of

∗

when we reach the critical value ˇ

∗

associated

with the short-ranged random-bond problem. Fol-

lowing the proposal in [360] a possible criterion de-

termining ˇ

∗

derives from the asymptotic form of

the fixed-point function K

∗

(u): setting ˇ

∗

equal to

the exponent 4 + n − / in the algebraic prefactor

of K

∗

(u) and using the simultaneous validity of the

“Flory” result (12.318) at ˇ

∗

one obtains ˇ

∗

= n/2,

resulting in the short-range exponent



d,n

4−d

4+n/2

. (12.320)

Further decrease of the correlator’s range does not

change this result, hence all short-range problems

are supposed to ﬂow to a fixed-point solution char-

acterized by ˇ

∗

. Although the use of the power-law

correction to K

∗

(u) as the relevant criterion to de-

termine ˇ

∗

is somewhat questionable, this scheme

does reproduce the correct value 

1,1

=2/3 for the

random polymer problem in 2D space. The scheme

adopted in [357] can be extended to follow the same

philosophy regarding the evolutionof the long-range

exponent 

d,n

to the short-range result 

d,n

;thein-

crease in ˇ

∗

should be stopped at a different value

∗

=0.801 for n =1andˇ

∗

=1.663 for n =2.These

values deriving from the numerical solution of the

fixed-point function (and hence involving all scales)

are larger than the result ˇ

∗

= n/2 emphasizing the

tail of the correlator.

The same result (12.320) has been found via a dif-

ferent route based on physical arguments and scaling

estimates[17]:Theargumentstarts with the observa-

tion that the elastic and pinning energies competing

for the manifold’s state involve separate parameters,

elasticity but no disorder on the one hand, and dis-

order but no elasticity in the disorder term. Second,

the disorder energy is expressed with an Ansatz con-

sidering separately thescaling arising from themani-

fold’s volume(∼ (L/L

)

dı

) and its transverse degrees

of freedom (∼ (/u)

), E

∼ U

(L/L

)

dı

(/u)

Thevolumeexponentı =1/2 then derives from the

requirement that E

does not depend on the elas-

ticity C; this is the usual volume scaling as it is also

assumed in the Flory-type analysis. Balancing dis-

order and elastic energies, this Ansatz provides the

exponent 

d,n

=(4−d)/(4 + 2˛). Second, we have to

find the exponent ˛ describing the inﬂuence of the

transverse degrees of freedom. The Flory-type anal-

ysis valid for a long-range correlator leads to a value

= ˇ(n)/2; on the other hand, we expect the cor-

relator to be renormalized at large distances in the

short-range random-bond problem and hence ˛

is not a priori known. For a rigid manifold, the de-

pendence of the disorder energy on the length L is

entirely dueto therandomadditionof forcesproduc-

ing the simple square root dependence on volume,

hence a stiff manifold is characterized by an expo-

nent ˛ = 0. The finite elasticity allows the medium

to wander in the transverse dimensions and to ex-

plore all the metastable states within the transverse

volume V

⊥

= u

. The number of available low lying

metastable states should thus scale with the trans-

verse volume V

⊥

, hence ˛

= ˛

n,with˛

afixed

constant independent of d and n. Using the exact re-

sult 

1,1

=2/3weobtain˛

=1/4, hence ˛

= n/4

and we recover the short-range exponent (12.320).

The large numerical value of the wandering expo-

nent 

d,n

, cf. (12.320), characterizes the strong effect

that quenched disorder exerts on an elastic mani-

fold. However, additional “microscopic” features of

the elastic manifold may reduce the effect of disor-

der. Here, we are interested in the behavior of Vortex

Matter where the elastic manifold is made from a pe-

riodic array (with periodicity a

) of interacting vor-

tices; both, the long-range interaction between the

vorticesand their periodicarrangement have drastic

consequences on the impact of quenched disorder

12 Vortex Matter 579

on the Abrikosov vortex lattice and reduce the wan-

dering exponent to zero.

Let us first concentrate on the effect of long-range

interaction. Neglecting the effect of screening, the

interaction between vortex segments decays only al-

gebraically ∝ 1/r, cf. (12.62), and the elastic tilt and

compression moduli become dispersive, cf. (12.68).

This dispersion in the elastic response lifts the ef-

fective dimensionality of the vortex system to four

dimensions where disorder is only marginally rele-

vant [10,346, 347]. As a consequence, the displace-

ment field u

(R, L)∝ ln(1 + R

+ L/a

)grows

only logarithmically, cf. Sect. 12.9.3, and the long-

range order of the Abrikosov vortex lattice is trans-

formed into quasi-long-range order in the presence

of disorder. The algebraic decay of the translational

correlationfunction



(R)



(0)∝R

−



depends

on the disorder parameter  , 



∝  , and algebraic

Bragg peaks in the structure factor survive in the

limit of weak disorder (cf. the discussion on quasi-

long-range order in Sect. 12.7.4).

The above behavior is cut off due to screening

on the scales R < , L < 

,butisresurrected

on larger scales due to the periodic nature of the

vortex manifold: for small displacements u < a

the lattice experiences a different disorder poten-

tial and, although taking place in the manifold’s

space, the motion can be considered as a transverse

one (note that a longitudinal motion, e.g., the mo-

tion of a string along itself, is not subject to pin-

ning forces as the manifold glides along the pin-

ning valley). However, when displaced a distance

u > a

the vortex lattice is exposed to the same

pinning potential and the disorder is effectively re-

duced. This feature is captured by a periodic correla-

tor K(u+a)=K(u)witha a lattice vector; hence,be-

sides random bond (short-range) and random field

(long-range) disorder a third type of random peri-

odic disorder turns out to be relevant [19–21]. This

type of random periodic disorder is realized in the

context of charge density wave pinning and pin-

ning of the periodic vortex lattice; the wandering

exponent takes the value 

CDW

=0andthedis-

placement field grows only logarithmically with dis-

tance, u

(R > R

)/a

∼ c ln(R/R

) [19–21], with

the crossover length R

defined via the condition

u

)∼a

. Note that within this random peri-

odic pinning regime the prefactor of the logarithm

is a number, [u(R)−u(0)]

/a



∼ 2c ln(R/R

c ≈ 0.0434, [21,361]) independent of the disorder

strength, producing a power-law decay R

−

(0,1)

in the

density–density correlator with an exponent 

(0,1)



(0,1)

]

c/2 ≈ 1.14, cf. (12.236) and (12.237) (see

[21,361] for a detailed discussion of nonuniversal

features). Hence the destruction of translational or-

der in the vortex lattice is quite subtle, with logarith-

mic regimes arising due to the long-range interac-

tion between vortex segments at intermediate scales

and due to the periodic nature of the manifold at

large scales. By virtue of this smooth algebraic de-

cay of translational order the asymptotic logarith-

mic regime has been termed the Bragg-glass scaling

regime [21] (characterized by the Bragg-glass expo-

nent 

= 

CDW

=0).

The problem of vortex pinning and creep in a

weak, uncorrelated random potential is intimately

related to the problem of elastic manifolds in dis-

ordered media.Vortex pinning is determined by the

competition between elasticity and disorder on short

scales, and hence the crossover length L

is a crucial

quantity in the determination of the critical current

density. Vortex creep involves the barriers separat-

ing metastable states. Near j

these barriers again are

determined by the short-scale properties of the elas-

tic manifold. Decreasing the driving force, the vortex

system probes increasingly larger length scales and

the manifold’s large-scale properties become impor-

tant; the details of pinning and creep in the vortex

system and their relation with the above results will

be discussed in the following sections. Finally,the in-

terplay of thermal and quenched disorder will lead

to the phenomenon of thermal depinning discussed

in Sect. 12.9.5.

12.9.2 Single Vortex Pinning

An individualvortex line subject to a disorder poten-

tial is described by the free energy (12.313): whilethe

elastic term tries to keep the vortex line straight, the

disorder term allows the vortex to lower its energy

as it aligns itself with the energetically favorableval-

leys in the pinning landscape. The energy gain due