Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.

600 G. Blatter and V.B. Geshkenbein
used expressions valid for anisotropic superconduc-
tors here). Note that conventional superconductors
with a small value for Gi belong to the class of strong
pinning material.
At high temperatures beyond the depinning line
T > T
dp
the disorder potentialissmootheddueto in-
travalleythermalfluctuations;wedeterminethetime
averaged pinning energy following the same scheme
as for the single vortex pinning problem above (cf.
(12.397)) and find the expression
E(V)
2
t
≈
lat
2
+ u
2
th
V , (12.410)
with
lat
= /a
2
0
=
d
2
uK(u)/a
2
0
≈
4
/a
2
0
.Com-
paring the results at low and high temperature we
find that the thermal displacement u
2
1/2
th
takes over
the role of the pinning scale if we express the
disorder strength by the parameter
lat
(note that
the disorder parameter
lat
describes fluctuations
in energy, see (12.312), and therefore is not rescaled
due to thermal smoothing; the latter affects only the
pinning forces via the change of the length scale
r
pin
∼ → r
pin
∼u
2
1/2
th
of the disorder poten-
tial but leaves its energy scale unchanged). Further-
more,wehavetoreplaceu
2
1/2
th
for in the expres-
sion for the energy gain due to the Lorentz force.
These substitutions allow us to generalize the results
of Sect. 12.9.3 in a simple way, such as to include the
effects of thermal fluctuations. In particular, we can
combine the low and high temperature results into
one expression by defining the temperature depen-
dent effective pinning scale r
pin
(T)ofthedisorder
potential,
r
2
pin
(T) ∼
2
1+
u
2
th
2
=
2
1+
T
T
dp
. (12.411)
The expressions for the collective pinning
length R
c
(T), the pinning energy U
b
c
(T) ∼
c
66
[r
pin
/R
c
(T)]
2
V
c
(T), and the critical current den-
sity j
c
(T) ∼ [r
pin
/R
2
c
(T)]j
0
then take the form
R
c
(B, T)
a
0
∼ (12.412)
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
exp
c
B
B
sv
1+
T
T
dp
2
3/2
, a
0
< R
c
(T) < ,
a
0
B
B
sv
1+
T
T
dp
2
3/2
, < R
c
(T) ,
U
b
c
(B, T)
U
c
∼ (12.413)
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
exp
3c
B
B
sv
1+
T
T
dp
2
3/2
, a
0
< R
c
(T) < ,
2
B
H
c
2
3/2
B
B
sv
1+
T
T
dp
2
2
, < R
c
(T) ,
j
c
(B, T)
j
c
∼ (12.414)
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
exp
−2c
B
B
sv
1+
T
T
dp
2
3/2
, a
0
< R
c
(T) < ,
j
0
j
c
2
B
B
sv
−3
1+
T
T
dp
−11/2
, < R
c
(T) .
In order to obtain the explicit dependence on the
magnetic field B and on temperature, we have sub-
stituted
L
c
a
0
r
2
pin
2
→
B
B
sv
1+
T
T
dp
2
1/2
(12.415)
in the above formulae. Finally, the temperature de-
pendent crossover fields B
sv
(T)andB
sb
(T) are given
by the expressions
B
sv
(T) ∼ B
sv
exp
−2c
1+
T
T
sv
dp
3
(12.416)
and
B
sb
(T) ∼ B
sv
1+
T
T
dp
−2
×
ln
2
j
c
j
0
1+
T
T
dp
−2
2/3
(12.417)
and decrease rapidly with increasing temperature
T upon crossing the depinning line B
dp
(T), see
Fig. 12.32.
12 Vortex Matter 601
12.9.6 Anisotropic Material
The generalization of the above results (12.413),
(12.414),and (12.415)to the anisotropicsituation us-
ing the scaling rules (12.170) is straightforward and
involves the substitutions
j
c
→ j
c
c
, U
c
→ U
c
c
,
H
c
2
→ H
c
2
(# ) , B
sv
→ B
sv
(# ) ,
T
dp
→ T
dp
(# ) , (12.418)
with the field rescalings H
c
2
(# )=H
c
c
2
/"
#
, B
sv
(# )=
B
c
sv
/"
#
and the rescaled depinning temperature
T
dp
(# )=2
√
""
0
2
("
#
B/¥
0
)
1/2
. However, the scal-
ing approach is limited to phenomena involving
length scales smaller than , i.e., the regime R
c
<
when discussing pinning; rescaling the condition
R
c
< we obtain the constraint
B < B
sc
≈ H
c
2
(# )
j
c
c
j
0
ln
2
j
c
c
j
0
2/3
. (12.419)
12.9.7 Layered Superconductors
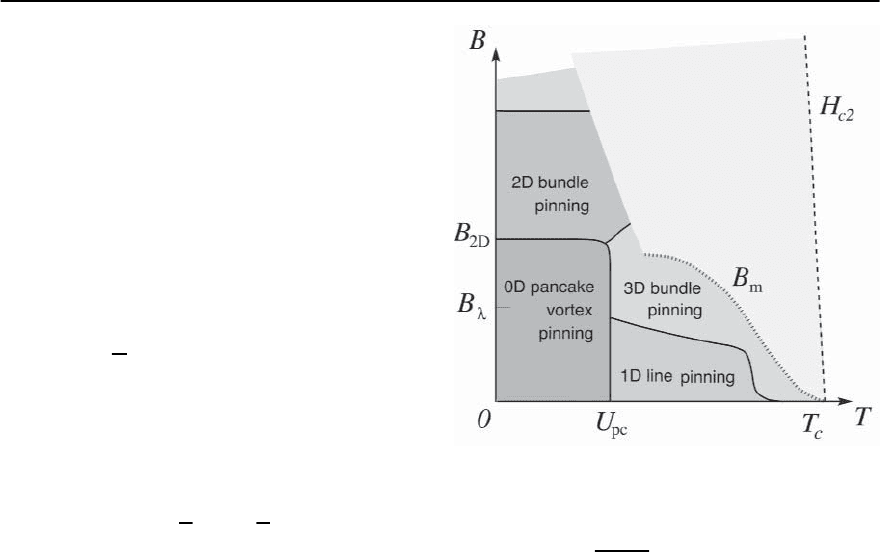
Pinning and creep in layered superconductors re-
quire a special discussion as the discreteness of
the structure can modify the results obtained for
a continuous anisotropic description [64,324]. We
assume that pinning is due to the collective action
of weak point-defects and consider the situation
with the magnetic field B aligned with the mate-
rial axis. Depending on the strength of the pin-
ning and on the magnitude of the magnetic field
B, the collectively pinned object as well as the nu-
cleus for the creep-type motion can take any form
between a zero-dimensional pancake vortex and a
three-dimensional vortex bundle. Let us start with
the usual continuous anisotropic description and
consider an isolated vortex line. The length of the
collectively pinned segment is given by (12.329),
L
c
c
∼ "
4/3
("
2
0
2
/ )
1/3
. For weak enough pinning (
small) we will have L
c
c
> d and the collectively
pinned object is a line segment. Second, in order
to neglect the interaction between the vortex lines
the magnetic field has to be weak enough such that
Fig. 12.33. Schematic pinning diagram for a layered su-
perconductor: strong pinning leads to 0D pancake-vortex
pinning and 2D pancake-vortex bundle pinning. Decreas-
ing the material anisotropy or the disorder such that
" > "
ca
∼ (d/)
U
p
/E
em
the 0D and 2D strong pinning
regimes vanish and we remain with the 1D line and 3D
bundle-pinning regimes characteristic for the anisotropic
material, cf. Fig. 12.32. The elastic approach used in the
determination of the various pinning regimes is limited
to the low-temperature low-field regime below the melting
line
L
c
c
< "a
0
. Together,we find the requirements for sin-
gle vortex line pinning to be
d < L
c
c
< "a
0
, 1D pinning . (12.420)
Increasing the magnetic field B such that "a
0
< L
c
c
we enter the regime of 3D bulk pinning,
d, "a
0
< L
c
c
, 3D pinning . (12.421)
We now increase the pinning parameter (or de-
crease the anisotropy parameter "); as the collec-
tive pinning length L
c
c
drops below the interlayer
distance d the line elasticity cannot compete any
longer against the pinning force and we enter the
strong pinning regime where pancake vortices are
pinned individually. In addition, we have to make
sure that the intraplanar interaction energy between
602 G. Blatter and V.B. Geshkenbein
the pancake vortices is smaller than the pinning en-
ergy U
pc
=
d
2
of an individual pancake vor-
tex, c
66
2
d < U
pc
. Combining these results the re-
quirementsfor single pancake-vortexpinning are (cf.
Fig. 12.33)
L
c
c
< d , B < B
2D
∼
U
pc
"
0
d
H
c
2
, 0D pinning .
(12.422)
Note that within the weak collective pinning scheme
the pinning energy U
pc
=
d
2
of an individual
pancake vortex still derives from many competing
point-like pinning centers.
Increasing the magnetic field B such that a
0
<
d"
0
/U
pc
the possibility of 2D collective pinning
arises. In this case all the pancake vortices within
aradiusR
c
> a
0
relax collectively to the under-
lying pinning potential. The collective pinning ra-
dius R
c
is obtained from the elastic-disorder energy
balance, c
66
d (/R
c
)
2
R
2
c
∼ (R
c
/a
0
)U
pc
,henceR
c
∼
a
0
("
0
d/U
pc
)(/a
0
)
2
. A second requirement for the
existence of a 2D collective pinning regime is given
by the smallness of the interlayer coupling U
J
int
∼
c
44
(K ∼ /R
c
)(/d)
2
dR
2
c
∼ "
0
d(/)
2
(R
c
/a
0
)
4
as
compared to the intraplanar energy U
2D
int
∼ c
66
d
2
.
The two conditions then define the boundaries of the
2D collective pinning regime,
L
c
c
< d , a
0
< R
c
<
a
0
, 2D pinning .
(12.423)
When the anisotropy is large (i.e., for a small
anisotropy parameter " < d/ where the Joseph-
son tilt energy "
2
"
0
u
2
looses the competition against
the electromagnetic tilt energy "
0
d
2
u
2
/
2
)wehave
to account for the electromagnetic coupling between
thepancakevortices; comparing the electromagnetic
tilt energy ("
0
d
2
/a
2
0
2
)R
2
c
with the intraplanar shear
energy U
2D
int
weobtain themodifiedconditionR
c
< .
Note that pinning is strong when compared to tilt
deformations but weak compared to the intrapla-
nar shear interactions. The 0D and 2D strong pin-
ning regimes vanish (simultaneously) as the mate-
rial anisotropy (or the disorder potential) is pushed
beyond "
ca
∼ (d/)
U
p
/E
em
.
Finally, for large fields such that R
c
>
√
a
0
we
enter the 3D collective pinning regime,
L
c
c
< d ,
a
0
< R
c
,
B
2D
2
2
U
pc
"
0
d
1/3
< B 3D pinning. (12.424)
The latter condition is equivalent to the previous con-
dition "a
0
< L
c
c
; the boundary to the 3D collective
pinning regime does not depend on the interlayer
distance d and is the same whether it is reached
from the 1D or from the 2D-pinning regime. Note
that an additional 1D-pinning regime appears at low
fields when pinning is weakened by thermal fluctua-
tions [323].
The complete description of pinning and creep in
layered superconductorsfollows the same scheme as
discussed in Sects. 12.9.1–12.9.6 above for the case
of isotropic and continuous anisotropic materials;
here, we wish to concentrate on some additional as-
pects which are peculiar to the layered situation.One
of these aspects is the strong dispersion in the elec-
tromagnetic tilt interaction manifesting itself in the
limit of large anisotropy (small anisotropy parame-
ter " d/). This dispersion is responsible for the
appearance of a first-order like jump in the pinning
length L
c
versus disorder strength in the small induc-
tion regime [323] (a similar jump between different
pinning regimes appears at high fields [421]): while a
large disorder potential produces 0D pancake-vortex
pinning with L
c
= d, decreasing the disorder leads
to a jump in L
c
with a large value L
c
> , placing the
pancake-vortex system into the 1D pinning regime.
A second aspect we wish to address here is a con-
sequence of the weak interaction between pancake
vortices at small magnetic fields: the elastic poten-
tial between pancake vortices reaches a lower limit
in the electromagnetic coupling between layers. On
the other hand, no such limit applies to the disorder
strength which then can outplay the elastic coupling
between pancake vortices. In a strong disorder po-
tential the 0D pancake vortices are quite free to opti-
mize their pinning energy by exploring large regions
of the disorder landscape; this probing of the dis-
tribution of low-lying states then leads to a further
enhancement of strong pinning. In the following, we
present a refined analysis of single pancake-vortex
pinning where we combine the two new aspects dis-
cussed above.
12 Vortex Matter 603
In order to simplify the discussion we consider
the decoupled limit with a purely electromagnetic
interaction (in a real material this corresponds to
the limit " d/ where the electromagnetic cou-
pling dominates over the Josephson coupling). The
presence of point disorder leads to a distortion of
the vortex line with a typical relative displacement
u between neighboring pancake vortices. The op-
timal pinning state is determined by the competi-
tion between the elastic and the pinning energies.
The deformation u of the vortex line on a length
L costs an energy E
el
(u, L) ∼ "
l
(u, k
z
∼ 1/L) u
2
/L
with the stronglydispersive elasticity"
l
(u < , k
z
)=
("
0
/2
2
k
2
z
) ln[1+
2
k
2
z
/(1+u
2
k
2
z
)].On the other hand,
when adjusting to the disorder potential, a vor-
tex segment of length L gains the pinning energy
E
pin
(u, L) ∼|E
0
(u)|
L/d ,whered is the layer sepa-
ration and E
0
(u) is the deepest minimum a pancake
vortexcansettleinwithintheareau
2
.Thisenergy
is determined by the condition u
2
E
0
dEg(E) ≈ 1,
where g(E) is the distribution of pinning energies,
which for a large number of defects we assume to be
Gaussian,
g(E)=
1
√
U
p
2
exp
−
E
2
U
2
p
%
. (12.425)
Here, U
p
quantifies the disorder strength, in the col-
lective pinning scenario, U
p
≈
2
d.Foru
(strong pinning) each pancake vortex can explore
many minima and settle in the lowest available state
E
0
(u) ∼ −U
p
ln
1+
u
2
2
1/2
. (12.426)
Introducing the energy scale E
em
= "
0
d
2
/
2
,wear-
rive at the vortex free energy f per unit length (cf.
(12.323)),
f (u , L) ∼
E
em
d
ln
1+
2
L
2
+ u
2
u
2
2
+
E
0
(u)
d
7
d
L
.
(12.427)
Minimizing f with respect to u and L provides us
with the optimal pinning state. For strong pinning
the minimum is realized by the 0D pancake-vortex
configuration (L = d) and minimizing (12.427) with
respect to u we obtain the optimal search area [422]
u
2
g
≈
2
U
p
E
em
ln
U
p
E
em
−1/2
ln
2
2
E
em
U
p
−1
.
(12.428)
The activation barrier for pancake-vortex motion is
U
pc
=−E
0
(u
g
) ≈ U
p
ln
U
p
E
em
1/2
. (12.429)
Thisvalue islargerthanthenaiveestimatein (12.422)
above as the pancake vortex optimizes its energy by
exploring the various minima in the transverse di-
mension.Comparing the Lorentz force j(¥
0
/c)d with
the pinning force U
pc
/, we find the pancake-vortex
critical current density,
j
pc
≈ j
p
ln
U
p
E
em
1/2
, (12.430)
with j
p
= j
0
(U
p
/"
0
d).
In the weak-pinning situation U
p
< E
em
we have
u
g
∼ , E
0
≈ −U
p
, and it is energetically more favor-
able for the system to settle in the 1D pinning regime:
Minimizing f (u = , L)withrespecttoL,wefind
L
c
∼
d
4/3
E
em
U
p
2/3
, (12.431)
and the corresponding expressions for the pinning
energy U
c
and the critical current density j
c
follow
from the usual scaling arguments,
U
c
∼ U
p
d
2/3
E
em
U
p
1/3
,
j
c
∼ j
p
d
2/3
U
p
E
em
1/3
. (12.432)
Hence decreasing the pinning strength U
p
below the
electromagnetic energy scale E
em
triggers jumps in
the pinning length L
c
, the pinning energy U
c
,and
in the critical current density j
c
involving the large
factor (/d)
2/3
(E
em
/U
p
)
1/3
. Such jumps in the char-
acteristic quantities L
c
, U
c
,andj
c
can be triggered as
well via an increase in temperature: thermal fluctua-
tionssmear thepinning potential and thuseffectively
reduce the disorder strength,with the corresponding
first-order like thermal depinning transition taking
place at a temperature [323]
T
g
∼ U
p
ln
U
p
E
em
−1/2
. (12.433)

604 G. Blatter and V.B. Geshkenbein
Let us apply these ideas to the layered BiSCCO su-
perconductor: We can ignore the Josephson coupling
in our rough estimates if " < d/; with typical val-
ues d =15Å,(0) ≈ 2000 Å, and " < 1/150 this
requirement is marginally satisfied. The parameter
U
p
can be estimated from experiments measuring
the critical current density at low B and T; in layered
high-T
c
superconductors (BiSCCO) U
p
≈ 10 K,typi-
cally.Comparing with the electromagnetic elastic en-
ergy E
em
≈ 0.2 K one concludes that strongly layered
high-T
c
superconductors quite naturally generate a
strong-pinning situation with U
p
E
em
.
As usual, increasing the magnetic field or tem-
peraturecouplesthepancakevorticesintoa
2D collectively pinned structure (above B
2D
∼
(U
pc
/"
0
d)) or into a 1D collectively pinned line
(above T
g
∼ U
p
[ln(U
p
/E
em
)]
−1/2
). Similarly, de-
creasing the current density via creep couples the
pancake vortices along the c-axis below j
g
∼
j
p
(E
em
/U
p
)
1/2
[ln(
2
E
em
/
2
U
p
)]
1/2
ln(U
p
/E
em
)
−1/4
.
The details of this temperature and creep induced
coupling are quite non-trivial, involving variable-
range hopping arguments [323] known from trans-
port in doped semiconductors [423].
As discussed above, the 2D pinning regime
bridges the field regime B
2D
< B < B
2D
[(
2
/
2
)
(U
pc
/"
0
d)]
1/3
between the 0D strong and 3D
weak pinning regimes. The pinning energy U
b
c
∼
U
pc
R
c
/a
0
∼ "
0
d(B/H
c
2
)doesnotdependonthedis-
order parameter and the critical current density
j
b
c
∼ j
p
a
0
/R
c
∼ j
p
(B
2D
/B) smoothly extrapolates
the pancake-vortex pinning result to higher fields.
The analysis of creep at low current densities and
the inclusion of thermal smoothing at high temper-
atures follows the usual scheme [150] discussed in
Sects. 12.9.4 and 12.9.5 above.
12.9.8 Pinning and Creep Diagrams
Besides the thermodynamic phase diagrams dis-
cussed in Sects. 12.1 and 12.7, the pinning and creep
diagrams introduced above provide a further use-
ful characterization of disordered Vortex Matter, cf.
Figs.12.28, 12.32, 12.33. These diagrams describe the
crossover between the various pinning regimes and
are not of thermodynamic origin — rather they de-
scribe the situation under strong drive close to j
c
.
The richest diagram appears in layered material (see
Fig. 12.33) with 0D and 2D strong pinning regimes
involving individual and in-plane coupled pancake
vortices. Weakening the pinning forces by thermal
smoothing at high temperatures or increasing the
elastic forces by increasing the magnetic field pro-
duces a crossover to the intermediate and weakly
pinned 1D lines and 3D bundles. Decreasing the ma-
terial anisotropy (i.e., increasing ")the0Dand2D
strong pinning regimesshrink and vanishcompletely
at the critical value "
ca
=(d/)
U
p
/E
em
— the pin-
ning diagram evolvesinto that describing the simpler
continuous anisotropic case involving only 1D and
3D regimes, see Fig. 12.32. The depinning line T
dp
triggers a rapid collapse of the crossover fields B
sv
and B
sb
. The sliver of small bundle pinning between
B
sv
and B
sb
is narrow.
Finally, we can join the pinning diagram at j
c
(Fig. 12.32) and the thermodynamic phase diagram
Fig.12.3atj = 0throughthecreepdiagramFig.12.28,
see Fig. 12.34. Moving away from the critical cur-
rent density j
c
towards thermodynamic equilibrium
(where j = 0) we cross the various regimes of single
vortex creep, small bundle creep, large bundle creep,
and finally, at very small current densities, the sys-
tem ends up in the Bragg-glass regime. The three
dimensional diagram Fig.12.34 is very useful for the
understanding of the time evolution of the system.
Consider for example a typical magnetic relaxation
experiment where a sample is first cooled in zero
field to a point A =(j =0, H =0, T < T
c
)within
the phase diagram. Upon switching on a field H
ext
a
critical state is established within the sample and we
jump to the pointB =(j = j
c
, H = H
ext
, T).In the fol-
lowing,the critical state decays slowly in time and the
system evolves gradually through the various creep
regimes as indicated by the line until it reaches
equilibrium (C). While the system should end up in
the Bragg-glass regime, the time scales involved in
reaching this asymptotic regimes are large; within
an experimental waiting time t the system is able to
overcome barriers of height T ln(t/t
0
). With typical
(in the copper-oxides) barriers U
c
∼ 100 − 1000 K
and a logarithmic enhancement ln(t/t
0
) ∼ 25 the
currents can relax by a factor 25T/U
c
∼ 2−25(we
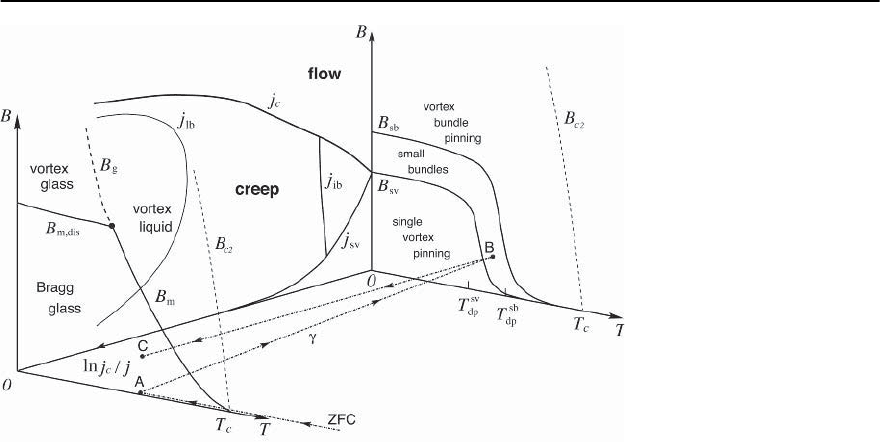
12 Vortex Matter 605
Fig. 12.34. Three-dimensional phenomenological phase diagram B–T–j for an anisotropic high temperature supercon-
ductor.The different regimes of pinning,creep,and flow divide the phase space into separate regions.The various pinning
regimes relevant at j ≈ j
c
are shown in the back. Upon decreasing the current density j the system probes the various
creep regimes on approaching equilibrium. Under equilibrium conditions (front) the currents in the system vanish. The
current axis also can be understood as a time axis via the relation j(t) ∝ [ln(t/t
0
)]
−1/
. The path of a typical magnetic
relaxation experiment is illustrated where a sample is cooled under zero field conditions to the point A. Switching on a
magnetic field a critical state is formed (B) which subsequently decays via creep ( ) towards the equilibrium Bragg-glass
state (C)
assume a glassy exponent ∼ 1) and it appears dif-
ficult to establish glassy order throughout the sam-
ple.
12.10 Correlated Disorder
The most prominent type of correlated disorder is
produced by columnardefectsintroducedartificially
into the material (typically YBCO or BiSCCO) by ir-
radiation with heavy ions.The columnar defects pro-
duce a marked increase in the criticalcurrent density
and a shift in the irreversibility line towards higher
temperatures and fields [29,30,89,90,424] (note that
proton-irradiation producing either point-like de-
fects or defect clusters leads to an increase in the
critical current density but leaves the irreversibil-
ity line unchanged [425]). The angular sensitivity of
these results with respect to the field-track orienta-
tion is much weaker forthe BiSCCO compound [424]
as compared to YBCO [29]. This different behavior is
attributed to the large difference in anisotropy be-
tween these materials [90,426].
Theoretically, the interplay between the vortex
system and a columnar defect structure has been
studied in much detail by Nelson and Vinokur [55]
and the competition between point disorder and
columnar defects has been analyzed in [427]. In the
following, we discuss some selected aspects of strong
pinning by columnar defects and then add a few re-
marksconcerning strongpinning due to twin bound-
aries.We adopt a continuous anisotropic description
for the material and assume both the magnetic field
and the tracks to be directed along the c-axis.
12.10.1 Columnar Defects
Pinning in a type-II superconductor is optimized
by introducing defects which trap the individual

606 G. Blatter and V.B. Geshkenbein
vortex lines all along while simultaneously destroy-
ing a minimal volume fraction of the supercon-
ducting material itself. A close to optimal defect
structure then is obtained by introducing colum-
nar defects into the material with cylinders of non-
superconducting material of diameter ∼ ,thevor-
tex core size (note that an ordered array of tracks
further optimizes pinning for a particular field value,
see [428]). The resulting pinning properties will be
highly anisotropic, with optimal pinning obtained
for a configuration where the magnetic field is
aligned with the linear defect structure. For this sit-
uation each trapped vortex gains an energy U
r
=
˛H
2
c
2
L,whereL is the size of the system along the
direction of the magnetic field and ˛ ageometry
factor (the index “r” refers to the properties of the
cylindrical rods). For weak enough fields the defects
outnumber the vortices and the interaction between
thevorticesissmallcomparedtoU
r
; within this sin-
gle vortex pinning regime we can expect to obtain
a critical current density j
c
≈ ˛j
0
, ˛ ∼ 0.1—1,
of the order of the depairing current density j
0
.Sec-
ond,since the thermal softening of the linear pinning
potential is much more gradual than for the point-
like pins one expects a reduction in the decrease of
the critical current density with increasing temper-
ature. Both effects have been observed on samples
of YBCO irradiated with high energy (∼ GeV) Sn
and Pb ions [29,30].The fast heavy ions produce lin-
ear tracks of damaged material due to their large
ionization energy-loss rate exceeding a few keV/Å.
High-resolution electron microscopy confirms the
formation of linear tracks of highly defected mate-
rial aligned with the beam direction. The resulting
defect structure can be modeled as a random array
of parallel normal cylinders of diameter 2r
r
≈ 50–70
Å embedded in a matrix of superconducting mate-
rial. The density n
r
= d
−2
r
of these columns is con-
veniently measured in terms of the matching field
B
¥
= ¥
0
/d
2
r
producing an equivalent density of vor-
tex lines in the superconductor. Typical irradiation
dosesasusedintheexperimentsproducevaluesfor
B
¥
between 1–5 T.
The pinning potential producedby a (large) cylin-
drical cavity of radius r
r
with < r
r
< has been
determined by Mkrtchyan and Schmidt [429],
r
(R) ≈ −"
0
ln
R
2
R
2
− r
2
r
, r
r
+ < R <
(12.434)
(the above result is easily obtained using the con-
cept of image charges from electrostatics and sum-
ming the ln-interaction potential from three aligned
charges, two positive ones placed at 0 and at R and
anegativechargeatr
2
r
/R). Cutting the above expres-
sion at the distance away from the cavity we obtain
the depth
r
(0) ≈ −"
0
ln
r
r
, < r
r
, (12.435)
of the pinning potential (this result derives from cut-
ting the vortex currents on the defect radius r
r
in-
stead of the core radius ). In order to reach an op-
timal pinning state the vortex lattice has to deform
locally at a cost of c
66
(d
r
/a
0
)
2
a
2
0
,whered
r
is the mean
separation between the tracks. A comparison of the
shear and pinning energies allows us to determine
the field regime B < B
r
where the individual vor-
tices can accommodate to the defect structure,
B
r
≈ 4B
¥
. (12.436)
Increasing temperature, the vortex core becomes
larger than thediameter of the cavity and the pinning
energy can be estimated from the gain in condensa-
tion energy when the vortex and the (small) cavity
overlap,
r
(0) ≈ −"
0
r
2
r
2
, r
r
< ; (12.437)
for a small cavity the pinning energy is reduced by a
factor r
2
r
/
2
. A further characteristic of the pinning
potential is the extended tail
r
(R < ) ≈ −"
0
r
2
r
/R
2
.
The critical current density j
c
can be obtained
from the force balance equation and is close to the
depairing value
j
c
(T < T
r
) ≈ j
0
, j
c
(T > T
r
) ≈
r
r
2
j
0
,
(12.438)
with the crossover temperature T
r
/T
c
=1−(
2
0
/r
2
r
)
determined by the condition (T
r
)=r
r
.Usingpa-
rameters appropriate for YBCO (
0
≈ 12 Å, r
r
≈
12 Vortex Matter 607
30 Å) we obtain the estimate T
r
≈ 0.8 T
c
.Above
T
r
the pinning potential decreases with increasing
temperature and hence also the crossover field B
r
limiting the accommodation of the individual vortex
lines to the columnar pins decreases,
B
r
(T) ≈
r
r
2
B
¥
∝
1−
T
T
c
. (12.439)
At large temperatures T the pinning potential is
strongly renormalized by thermal fluctuations. The
mean squared fluctuation amplitude u
2
increases,
first still limited to a region around the track, then
expanding to cover many tracks, until it reaches the
value u
2
≈Ta
0
/2
√
""
0
set by the neighboring
vorticesin the lattice.In the course of this expansion
the vortex line averages the disorder potential over
an increasingly larger area and the critical current
density decreases accordingly. In the following, we
discuss this thermal smoothing through the various
regimes — we will see that correlated disorder helps
in keeping the critical current density high as com-
pared to uncorrelated disorder due to point defects.
A useful tool in the discussion of thermal fluctua-
tions is the vortex–boson analogy, mapping the clas-
sical statistical mechanics of the vortex system to the
quantum statistical mechanics of 2D bosons through
the identification T ↔
B
, z ↔ , L ↔
B
/T
B
,and
"
l
↔ m, cf. Sect. 12.7.7 above; note the columnar
tracks produce a static disorder potential within the
quantum formulation. The problem of vortex pin-
ning onto a columnar track maps to the problem of
binding a particle in the potential "
r
(R)andwehave
to solve the Schr¨odinger problem
T
2
2"
l
∇
2
R
+
r
(R)
¦ (R)=−e
B
¦ (R) . (12.440)
Assuming a rectangular potential of depth
r
and
extent r
r
≈ max(r
r
, ) the binding energy is
given by e
B
=
r
[1 − cT
2
/2
r
"
l
r
2
r
]withc acon-
stant of order unity. If the potential is shallow
(or T is large) the binding is exponentially weak
[430], e
B
∼ (T
2
/"
l
r
2
r
)exp(−T
2
/"
l
A)withA =
−
∞
0
dRR"
r
(R)=−
r
r
2
r
/2. As a result, we obtain
the renormalized pinning energy
"
r
(T)=
r
f
T
T
r
dp
, T
r
dp
=
r
r
√
2
√
"
l
r
, (12.441)
with f (x 1) = 1 − x
2
and f (x > 1) ∼ x
2
exp(−x
2
).
Taking account of the slow decay of the pinning
potential −
r
(R) ≈ −"
0
r
2
r
/R
2
,wehavetosolvethe
Schr¨odinger equation for a particle in a shallowlong-
range potential and we obtain a binding energy of
the form (12.441) with T
r
dp
=(
√
2r
r
/)
√
"
l
r
and
f (x > 1) ≈ exp(−x) [150]; the slow decay of the pin-
ningpotentialstrongly reduces itsthermally induced
smoothing.
The renormalization of the pinning energy due to
thermal fluctuations implies a corresponding reduc-
tion in the crossover field,
B
r
(T) ≈
r
2
r
2
B
¥
exp[−(T/T
r
dp
)] . (12.442)
Similarly, thermal fluctuations lead to a reduction in
the critical current density: Increasing the tempera-
ture beyond T
r
dp
thevortex line wanders away fromits
column. In order to find the mean squared thermal
amplitude u
2
th
we consider again the 2D quantum
problem of a particle trapped in a shallow potential.
The binding energy e
B
is easily converted to a local-
ization length for the wave function (l
2
∼
2
/me
B
)
and using our mapping rules bridging between the
2D-Bose system and the vortex system we obtain
u
2
1/2
th
≈ r
r
T
T
r
dp
exp[T/2T
r
dp
] . (12.443)
Combining (12.441) and (12.443) we obtain the fluc-
tuation corrected critical current density (we assume
T
r
> T
r
dp
),
j
c
≈
r
2
r
2
T
r
dp
T
j
0
exp[−3T/2T
r
dp
] , T
r
dp
< T < T
dl
.
(12.444)
As the thermal amplitude u
2
1/2
th
grows beyond the
mean rod spacing d
r
the vortex line samples many
tracks and becomes collectively pinned by fluctua-
tions in the track density; the condition u
2
th
∼ d
2
r
determines the delocalization temperature T
dl
,
T
dl
∼ T
r
dp
ln
d
2
r
r
2
r
. (12.445)
608 G. Blatter and V.B. Geshkenbein
Note that both expressions T
r
dp
and T
dl
depend on
temperature and their onset values (T
r
dp,0
and T
dl,0
)
have to be determined self-consistently, cf. (12.401).
Next we determine the fluctuation amplitude
u
2
1/2
th
in the high temperature regime T > T
dl
.
We then have to find the localization length for a
particle subject to a random potential U (R) charac-
terized by a correlator U
r
(R)U
r
(R
) =
r
ı(R − R
)
with
r
=
2
r
r
4
r
/d
2
r
(here,
r
denotes the unrenormal-
ized pinning potential). Analyzing the Schr¨odinger
equation (12.440) with
r
(R)replacedbyU
r
(R)we
can estimate the localization length by compar-
ing the kinetic (T
2
/2"
l
u
2
th
) and potential energies
(
r
r
2
r
/d
r
u
2
1/2
th
),
u
2
1/2
th
∼ d
r
T
T
dl
2
, T > T
dl
. (12.446)
Above T
dl
both the pinning energy and the critical
current density decay more slowly with temperature,
pin
∼
r
r
r
d
r
2
T
dl
T
2
,
j
c
∼
r
"
0
d
r
r
r
d
r
2
T
dl
T
4
j
0
. (12.447)
At high temperatures the single vortex pinning
regime extends up to fields where the thermal am-
plitude u
2
th
of the individual lines remains smaller
than the thermal amplitude of fluctuations u
2
th
≈
Ta
0
/2
√
""
0
of the vortex lattice,
B < B
r
∼ B
¥
r
r
d
r
2
r
"
0
T
dl
T
6
, T > T
dl
.
(12.448)
Accounting for the temperature dependence of T
dl
the crossover field B
r
∝ B
¥
(1−T/T
c
)
6
decays rapidly
on approaching T
c
.
The results (12.438), (12.444), (12.447) describe
the decrease of the single vortex critical current den-
sity with increasing temperature: At low tempera-
tures T < T
r
the critical current density is of the or-
der of the depairing current density, (12.438).Above
T
r
the critical current density decreases, first due
to the reduction in
r
, (12.438), then, above T
r
dp
,due
to thermal fluctuations, (12.444), and finally, above
T
dl
, due to delocalization from the individual rods
and crossover to collective pinning by many rods,
(12.447).Comparing the efficiency of vortex pinning
by correlated columnar disorder with that of uncor-
related disorder due to point-like defects we note the
advantage offered by the irradiation technique: for
low fields and temperatures the vortices can take ad-
vantage of strong pinning centers. At elevated tem-
peratures, thermal smoothing efficiently wipes out
the effect of point-like disorder and strongly reduces
the pinning strength of an individual columnar de-
fect; on the other hand, the collective pinning due
to many columnar tracks is less susceptible to ther-
mal smearing, resulting in a slower decay of j
c
with
increasing temperature.
Various extensions complete the pinning diagram:
At high temperatures vortex bundles are pinned col-
lectively by fluctuations in the track distribution.
Similarly, pinning involves vortex bundles at high
magnetic fields. However, plastic pinning intervenes
in an intermediate field range just above the match-
ing field B
¥
, see [150] for details.
A further topic of interest is vortex creep. The
generic geometry of the creep nucleus is a half loop
with an aspect ratio following from the competi-
tion between the line elasticity and pinning, u
hl
∼
(
r
(T)/"
l
)
1/2
L
hl
, and a size determined by the energy
gain due to the Lorentz force j¥
0
L
hl
u
hl
/c,
u
hl
(j) ∼
r
(T)
"
l
j
0
j
,
U
hl
(j) ∼
r
(T)
√
"
l
r
(T)
"
0
j
0
j
. (12.449)
As j decreases these half-loops expand, transform
into double-kinks as they link up to the neighbor-
ing columns (u ∼ d
r
) and finally hop large distances
u d
r
to search for an optimal track; the careful
analysis again involves variable range hopping argu-
ments [55] known from transport in doped semicon-
ductors [423].
A particular characteristic of pinning by colum-
nar tracks is the locking of vortices into the track
direction [38, 431]: Tilting the field away from the
track direction produces kinks with an energy cost
E
kink
≈ d
r
√
2"
l
r
(T). Multiplying with the num-
ber of kinks L||/d
r
and dividing by the vortex
12 Vortex Matter 609
volume La
2
0
we obtain the trapping energy density
E() ≈
√
2"
l
r
(T)||/a
2
0
. Rewriting this term as an
energy gain of vortex lines in the presence of colum-
nar defects, ıE ≈ −("
l
/2a
2
0
)( −
t
)
2
Ÿ(
t
− )we
obtain the trapping angle
t
=
2
r
"
l
1/2
. (12.450)
Adding this energy gain to the Gibbs free energy den-
sity and minimizing with respect to the angle at a
given angle
H
of the external H-field we obtain the
locking angle
L
=
4"
l
¥
0
H
t
. (12.451)
For angles
H
<
L
the vortices remain fully locked
to the columnar tracks.
The trapping of vortices onto columnar tracks
has been tested in crystals irradiated at a finite an-
gle
r
(measured from the c-axis). The magneti-
zation loop is measured twice, once with the field
aligned parallel to the tracks (
B
=
r
)andasec-
ond time with the vortices aligned in opposition to
the tracks (
B
=−
r
, i.e., the vortices run within the
plane defined by the tracks and the c-axis but point
in the direction opposite to the tracks); the angu-
lar anisotropy then acts equally in both geometries.
Comparing the two magnetization curves allows to
estimate the pinning efficiency of the tracks and its
angular sensitivity. With a track angle
r
=30
◦
,ex-
periments on YBCO [29] show very different mag-
netization curves while the same experiment carried
out on an irradiated BiSCCO sample [424] shows lit-
tle difference between the two geometries. This re-
sult can be easily understood within the scaling ap-
proach: after rescaling to an equivalent isotropic sys-
tem the magnetic field and the tracks are redirected
towards the c-axis with the new isotropized angles
˜
r,B
=arctan(" tan
r,B
). The trapping cone is given
by the isotropized version of (12.450),
˜
t
=
2
˜
r
/ ˜"
l
,
where the isotropized pinning energy and line ten-
sion take the values
˜
r
= "
0
and ˜"
l
= "
0
and de-
notes the pinning efficiency. The latter does not de-
pend on the anisotropy and hence the rescaled trap-
ping cones have a similar width
˜
t
≈
2.Whilethe
track-aligned vortices obviously reside in the trap-
ping cone (and hence are strongly pinned), the vor-
tices in the opposite geometry may or may not end
up in the trapping cone: in YBCO the anisotropy is
moderate and the redirected vortices end up outside
the trapping cone, while the large anisotropy in BiS-
CCO redirects the vortices (and the tracks) very close
to the c-axis allowing for an efficient vortex trapping
and pinning.The width of the trapping cone depends
on temperature, mainly via the temperature depen-
dence of the pinning energy "
r
. Indeed, increas-
ing the temperature reduces the pinning strength "
r
and hence narrows the trapping cone. This explains
the reappearance of the angular sensitivity in BiS-
CCO observed at high temperatures [432]. The same
scheme can be used to analyze the pinning efficiency
of randomly splayed tracks [433].
12.10.2 Twin Boundaries
Another type of correlated disorder is due to twin-
ning planes (TPs) which naturally appear in or-
thorhombic YBCO crystals. In general, such planar
perturbations scatter electrons and thus define a fi-
nite transparency for motion ofcarriers across — the
boundary acts as a tunnel junction.In high temper-
ature superconductors the combination of d-wave
symmetry and scattering suppresses superconduc-
tivity: hence twinning planes in YBCO, in addition
to introducing a finite transparency (corresponding
to a local perturbation ım in the GL functional) also
produce a suppression of the order parameter (a lo-
cal perturbation ı˛ [434]); which of the two mech-
anisms is more efficient in pinning the vortices is
difficult to tell and furthermore temperature depen-
dent.
The attraction of (parallel aligned) vortices to
twinning planes leads to an enhanced vortex den-
sity along the twin boundaries, as clearly observed
inBitterdecorationexperiments[169].Therelevance
of the twin boundaries for the pinning problem has
been indicated early on in resistivity [28, 328, 435],
torque [436], and magnetization [437–439] experi-
ments and more recently [440] via the angle depen-
dence of the c-axis critical current density j
c
(, B)
when the magnetic field B = B(cos, sin , 0) is ro-
tatedwithin the ab-plane.Pushing vortices outof this
correlated pinning potential (with a driving current
