Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

610 G. Blatter and V.B. Geshkenbein

parallel to the twins) is hard and the critical current

enhancement in the geometry j  TPs is quite sub-

stantial, with values of order 10 [440] up to 25 [441]

measured at 77 K. Such a rather strong pinning is

also suggested by low-temperature scanning tunnel-

ing experiments resolving the vortex structure near

a twin boundary, where the current density required

to push a ﬂux line out of an individual twin bound-

ary potential well is of the order of the depairing

current density [442]. Furthermore, thermal depin-

ning out of the well is strongly suppressed: following

argumentssimilarto thoseused in the contextof pin-

ning by columnar tracks (see Sect. 12.10.1) one de-

rives [150] a critical current density decaying ∝ T

−4

as compared to the exponential decay produced in

the competition of thermal ﬂuctuations with uncor-

relateddisorder (again,the mapping to quantum me-

chanics is conveniently used).

Vortex pinning along the twin boundary direc-

tion (as probed with a current j ⊥ TBs) is a more

subtle issue. Various competing effects seem to be at

work which enhance/reduce the pinning within the

twin boundaries as compared to the bulk: while the

elongation of the vortex core (implying a reduced

suppression of the order parameter in the vortex

center, cf. the discussion in Sect. 12.5.2 and [196])

tends to decrease the pinning of the vortex within

the twinning plane, one expects an enhanced defect

density within the twin boundary region generating

the opposite effect. A generic mechanism produc-

ing an enhanced pinning within the plane (as com-

pared to pinning in the bulk) is again due to thermal

smoothing at high temperatures: while pinning of

a vortex line decays exponentially with temperature

in the bulk (cf. (12.405) and (12.405)), the thermal

motion of a vortex line confined to a plane is sup-

pressed, see (12.400), and hence thermal smoothing

of the disorder potential within the twin boundary

plane is reduced with a critical current density de-

caying ∝ T

−7

(note the difference between thermal

depinning within the well due to smoothing of un-

correlated disorder as compared to thermal depin-

ning out of the well described above). Experiments

report conﬂicting results, on the one hand provid-

ing evidence for easy-ﬂow channels [443,444],while

others are favorably explained in terms of enhanced

pinning within the twinning planes [28,445]. These

contradicting results may find a consistent interpre-

tation in terms of the above thermal smoothing sce-

nario: experimentson the samesamplecarried out at

low and high temperatures exhibitvortex channeling

along the twinning planes at low temperatures, while

large (relative to the bulk value) barriers to ﬂux mo-

tion in the twin planes are observed at higher tem-

peratures [446].

A further interesting aspect of twin boundary

pinning is vortex trapping and vortex locking, cf.

(12.450) and (12.451) forthe analogousphenomenon

in the context of pinning by columnar tracks.Indeed,

the enhanced pinning described above is effective as

long as the vortices are sufficiently aligned with the

twinning planes such that finite vortex segments re-

main trapped [38,431]. Typical trapping angles are

of order 10

◦

, while locking angles are found in the

sub-1

◦

regime [28,328,440].

12.11 Surface and Geometrical Barriers

While vortices find a thermodynamically stable state

in the superconductor at fields H > H

they can-

not form spontaneously within the bulk sample but

have to penetrate from the sample edge. This edge

represents a perturbation which produces a barrier

against vortex entry. For an ideal surface the barrier

vanishes only at the critical field H

> H

,whilein-

homogeneities in the surface facilitate vortex entry.

The vortex penetration into a bulk sample then is de-

layed to a penetration field H

with H

< H

Early studies of surface barriers are due to Bean and

Livingston [330] and Clem [447]. The appearance

of pronounced surface pinning in layered BiSCCO

has strongly revived interest in surface pinning and

creep [448]. Furthermore, the platelet type form of

BiSCCO single crystals produces geometrical barri-

ers generating a dome like ﬂux profile within the

sample[331–333].Below we summarizethemain fea-

tures of surface pinning and creep and then discuss

the nature and consequences of geometrical barriers.

12 Vortex Matter 611

12.11.1 Surface Barriers

Consider a ﬂux line running parallel to the

superconductor–vacuum interface at a distance x

(e.g.,with the vortex directed along ˆz and the surface

parallel to the yz-plane with a surface normal ˆx).The

boundary condition ˆx · [∇' +(2/¥

)A] = 0 tells

that no current crosses the superconductor–vacuum

interface and the vortex current is squeezed towards

the surface;following Bernoulli’s law the vortex is at-

tracted to the surface. For a quantitative analysis we

can adopt the idea of image charges from electrostat-

ics: placing an image vortex pointing along −ˆz at a

distance −x from the interface the boundary condi-

tion is satisfied. The interaction energy between the

vortex and its ghost image produces the attractive

Bean–Livingston potential



(x)=

(2x)−h

()]

4

(12.452)

= "

(/)−K

(2x/)] ,

where h

(x)=−(¥

/2

(x/)isthemagnetic

field associated with a vortex (the factor 1/2 restricts

the energy to the half space). A vortex penetrating

into the superconductor has to overcome the po-

tential 

(x). In the presence of an external field

H directed parallel to the vortex the Meissner cur-

rent j(x)=(c/4)@

[H exp(−x /)] pushes the vor-

tex into the sample and the total energy takes the

form



surf

(x, H)=−"

(2x/) (12.453)

+ H exp(−x/)]

4

This surface barrier has a maximum u

(H) ≈

[ln(H

/H) − 1] at a distance x

≈ (H

/H)from

the surface and vanishes only at the first penetra-

tion field H

≈ ¥

/4 ≈ H

(at fields of or-

der H

the order parameter is strongly suppressed

at the surface; using a Ginzburg–Landau descrip-

tion in the high- limit one can show that H

= H

is an exact result [449, 450]). At first penetration a

current j(x =0)≈ cH

/4 of the order of the

depairing current pushes the vortex into the sam-

ple. Note that at H

the vortex energy at the sam-

ple edge becomes equal to its energy in the bulk,



surf

(, H

) ≈ 

surf

(∞, H

),hence the vortex is ther-

modynamically stable for fields H > H

but can-

not penetrate until the barrier vanishes at H

.On

the other hand, real samples will usually exhibit in-

homogeneities producing local field enhancements

and reducing the first penetration field to a value

below H

Above H

vorticesrush into the sample until their

mutual repulsion matches their compression due to

the Meissner surface current. Following Clem [447]

we average the magnetic field over the intervortex

distance a

and split the sample into two regions, a

vortex-free surface region 0 < x < x

where Meiss-

ner currents ﬂow and a current-free vortex region

< x with an induction B. The field profile h(x)

follows from the London equation and decays ex-

ponentially from h(0) = H > H

at the surface

to h(x > x

)=B < H in the vortex region. Fur-

thermore, the Meissner current j(x)=(c/4)@

h(x)

should vanish at x

.SolvingtheLondonequation

in the vortex free regime with the Ansatz h(x )=

a exp(−x/)+b exp(x/) and enforcing the above

boundary conditions at x =0, x

we find the

field profile h(x)=Bcosh[(x − x

)/], in particular

H = Bcosh(x

/).Theposition x

of the front is fixed

by requiring that the “last” vortex penetrating does

not encounter a surface barrier, hence j(x =0)≈ j

and we obtain the second relation H

≈ Bsinh(x

/).

Given the external field H,thefieldprofilein thesam-

ple then is characterized by the induction B and the

front position x

in the form

B =



− H

, x

(H)=



H + H

H − H

. (12.454)

For H  H

we have x

≈ (H

/H) ≈ a

/4  a

for H  H

and the width x

of the vortex free re-

gion is indeed larger than the intervortex distance a

up to large fields of order H

Finally, we calculate the magnetization −4M =

H − B = H −(H

− H

)

1/2

≈ H

/2H,wherethelast

equation is an expansion for H  H

.Thismagneti-

zation reaches the scale of the equilibriummagneti-

zation −4M

≈ H

only at a field H ≈ H

≈

, close to the upper critical field. Note that the

magnetization loop is strongly asymmetric: on de-

creasing H (while keeping B constant) the front x

612 G. Blatter and V.B. Geshkenbein

moves towards the surface until B = H and the mag-

netization M =0vanishesuntilH changes sign (the

image forcepulls the vorticesoutof the sample keep-

ing B = H).

At finite temperature vortices can enter the sam-

ple for fields H < H

via thermally activated creep

through the formation of half-loops (of height l and

extending a distance u into the sample). Balanc-

ing the elastic energy ("

/l) against the pinning

("

u ln(u/)) and Lorentz force (¥

ju

/2c)ener-

gies we obtain (cf. (12.449) and [448])

u ≈ 

, U ≈





. (12.455)

In an anisotropic material the length l and energy

U are rescaled by the anisotropy parameter ".In

layered material such as BiSCCO the loop height

l ≈ "(j

/j) might be smaller than the layer separa-

tion d and penetration proceeds via single pancake-

vortex creep. Balancing again the surface barrier

d ln(u/) against the Lorentz force energy ¥

jdu/c

we obtain the creep characteristics

u ≈ 

≈ 

, U ≈ "

d ln

≈ "

d ln

(12.456)

wherewehaveexpressedtheMeissnercurrentj driv-

ing the creep in terms of the applied magnetic field,

j ≈ cH/4. Combining this result with the time

relaxation (12.302) we obtain the relation U(H

T ln(t/t

), from which we conclude that the effective

penetrationfieldH

decayswithtemperature or time,

(T, t) ≈ H

exp[−T/T

(t)] , T

= "

d/ ln(t/t

) .

(12.457)

Repeating the calculation of the induction (12.454)

with the new boundary condition for the current

density j(x =0)∼ j

exp[−T/T

(t)] we recover

the original expression (12.454) with H

replaced by

(T, t). The tail (H  H

(T, t)) of the magneti-

zation loop then decays with temperature or time

according to

−4M(T) ≈

∝ exp



−



, (12.458)

−4M(t) ∝





−2T/"

Note, that the tail decays faster than the penetration

field itself. As the hopping distance u increases be-

yond the front x

(H, H

(T, t)) the creep barrier sat-

uratesand the magnetization becomes reversible; the

condition u ∼ H

= x

≈ H

irr

defines the

irreversibility line

irr

(T, t) ∼





∼ H

exp(−2T/T

) , (12.459)

where the magnetization loop M(H)closeswhen

measured on a time scale t and at a temperature T.

Inserting this result into (12.459) we note that the

magnetization M has dropped to a value of order of

the equilibrium magnetization, −4M ∼ H

.Also,

inserting H

∼



irr

/ back into the expres-

sion for the front position x

∼ H

irr

one ob-

serves that the front has approached the boundary

up to a lattice constant, x

∼

√

irr

.Notethat,

depending on the field and time scale of the exper-

iment, the irreversibility temperature T

irr

(H, t) ≈

d ln(H

/H)/2ln(t/t

) may end up on either side

of the 2D melting temperature T

≈ "

d/70.

Finally, although the system behaves reversibly

at T > T

irr

(H, t), the resistivity (as probed via

a small transport current) is still activated,  ∝

exp(−U /T). The corresponding surface barrier U ≈

d/2) ln(H

/H) follows from (12.456) with the

driving current density j ∼ j

/u obtained from the

saturated hopping distance u ∼ x

∼ a

12.11.2 Geometrical Barriers

Consider a ﬂat superconducting sample of ellipsoidal

shape in the magnetic field H

arranged parallel to

the axis; then the induction B inthesampleandthe

applied field H

are related via the magnetization M

and the demagnetization factor n,

B = H

+4(n −1)M . (12.460)

In the Meissner state the field inside the supercon-

ductor vanishes and the magnetization loop rises

more steeply, −4M = H

/(1 − n). For a ﬂat (rota-

tional) ellipsoid of height d and diameter 2w the de-

magnetization factor is n ≈ 1−(/2)(d/2w), hence

−4M =(2/)(2w/d)H

and the magnetic moment

12 Vortex Matter 613

is enhanced by a factor ∼ w/d  1 (for a cigar

shape ellipsoid with d  w, n ≈ (d/2w)

ln(2w/d),

and n =1/3 for a sphere).

Quite often, ﬂat platelet like samples are analyzed

with the help of an idealized ellipsoidal approxi-

mation. However, the radius of curvature R at the

perimeter is quite different for an ellipsoidal shape

and for a platelet-shaped sample: the ellipsoid ex-

hibits a “sharp” edge with R

ell

≈ d

/w,whilethe

platelet’s edge is better approximated by a shelf of

width d and the corresponding radius of curvature

shelf

≈ d. This has quite severe consequences forthe

field enhancement at the sample edge: Consider the

magnetostatic problem for a superconducting wedge

with an opening angle 

in the Meissner state; the

external field H is arranged perpendicular to one of

the wedge’s planes. With ∇·B =0and∇∧B =0we

can express B = ∇¦ through the scalar field ¦ and

solve for the Laplace problem ¦ =0withNeumann

boundary conditions ∇

⊥

¦ = 0 in cylindrical coor-

dinates (, ' ) (we look for a solution in the form

¦ (, ' )=

[a cos(˛')+b sin(˛')] and impose

the boundary conditions @

¦ =0at' =0, 2 − 

to obtain ˛ = /(2 − 

)). Near the edge, the mag-

netic field diverges as B(, ' ) ∝ 

(

−)/(2−

)

and

fora sharp edge with 

= 0 we obtain the divergence

B(, ' ) ∝ 1/

√

. Cutting this divergence at the ra-

dius of curvature we obtain the field enhancement

edge

∼ H

(w/d) for the ellipsoid (in agreement with

the above analysisusingthe demagnetizing factorn),

while for the platelet sample the field enhancement

is parametrically smaller, H

edge

∼ H



w/d.

Let us determine the field and current configura-

tion in a ﬂatsample of strip-like geometry (extending

along y) subject to a perpendicular field H

directed

along the z-axis. We can ignore the details of the

sample’s thickness profile (d(x)) by integrating the

current density along the z-axis,

(x) ≡

d(x)/2



−d(x)/2

dzj

(x, z) , (12.461)

reducing the sample to a zero width strip extending

from x =−w to x = w. The magnetostatics problem

is solved via conformalmapping: We define the com-

plex function §( = x +iz) ≡ B

()+iB

()over

the complex -plane. Outside the sample the field

equations ∇·B =0and∇∧B = 0 are interpreted

as the Cauchy–Riemann equations for the complex

function §() which thus is analytic away from the

cut |x|≤w.Amp`ere’s law then relates the current

ﬂow J

(x) with the jump in B

(x, 0) = Re§(x, 0)

across the strip, B

(x, 0) = (2/c)J

(x), while the z-

component of the induction is required to vanish in

the Meissner state, B

(|x| < w, 0) = 0. Therefore,

§ is purely imaginary near the strip while § ∼ H

far away. The corresponding analytic function takes

the form §( = x +iz)=H





/(

− w

)andwe

obtain the current and field profiles of the Meissner

state

(|x| < w)=−

2

√

− x

(|x| > w, z =0)=H

|x|

√

− w

. (12.462)

Given the current profile in the sample we now can

determine the potential profile fora vortex penetrat-

ing the sample from the edge. For a ﬂat strip of con-

stant thickness d this potential takes the form (see

Fig. 12.35)



geo

(x)=

d +





) , (12.463)

where the first term is due to the vortex line en-

ergy, while the second term is the contribution from

the Lorentz force pushing the vortex into the sam-

ple. For H

= 0 a sharp barrier of height 

d rises

over the distance ∼ d from the edge as the vortex

line is being created (here, we ignore the presence of

an additional surface barrier).A finitefield produces

an energy gain as the vortex glides into the sample

and at H

=(d/2w)H

the vortex state has become

thermodynamically stable. However, the vortex pen-

etration is delayed by the geometrical barrier and

we need the “large” field H

≈



d/wH

in order to

produce the edge current density j

edge

≈ cH

/2d

necessary to compensate the vortex creation energy



. The geometrical barrier 

d is absent in a smooth

sample with an ellipsoidal profile: here, the line en-

ergy rises continuously from zero with increasing

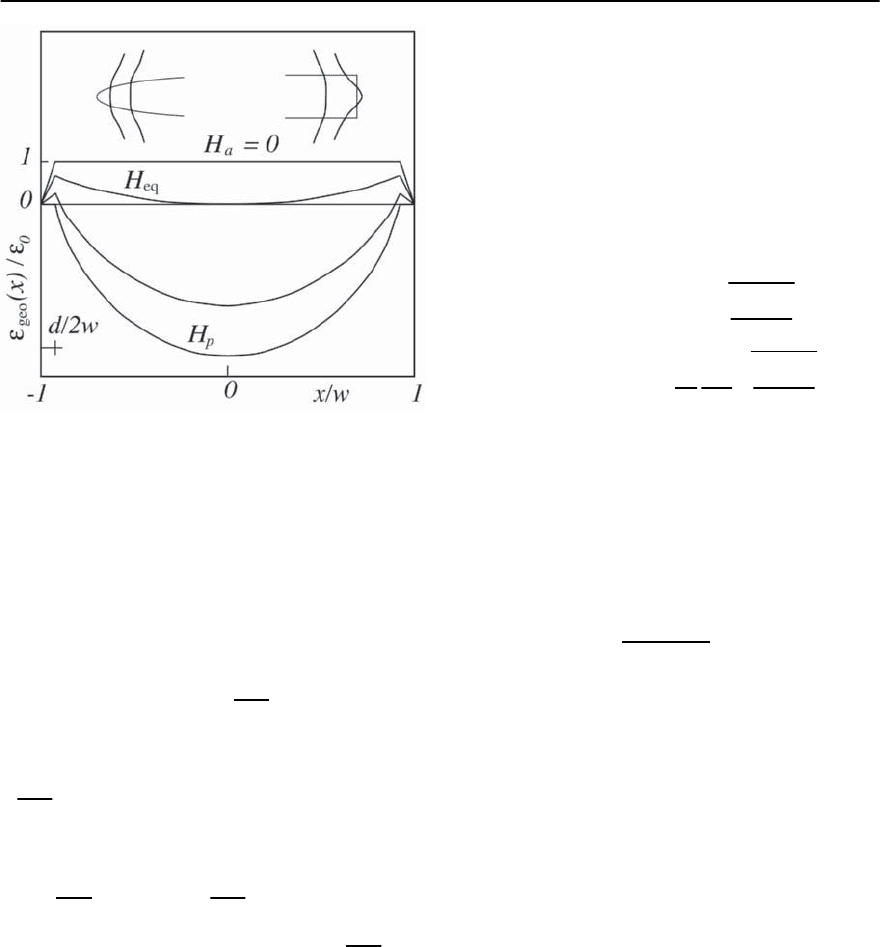
614 G. Blatter and V.B. Geshkenbein

Fig. 12.35. Vortex potential at various applied fields 0 ≤

≤ H

.AtH

= 0 the potential at the edges of the sam-

ple is assumed to drop linearly for simplicity. The inset

shows the penetration of a vortex into an elliptical-shape

sample (the vortex segment grows continuously and there

is no geometrical barrier) and into a shelf-shape sample

(the vortex segment grows rapidly over a distance ∼ d/2

resulting in a geometrical barrier)

sample thickness and the Lorentz force can match

the cost at H

=(d/w)H

; the penetration field H

for a ﬂat sample is enhanced over that for an ellip-

soidal sample by the factor



w/d due to the presence

of a geometric barrier.

Accounting for the additional surface barrier the

penetration field H

is shifted to the value H

≈



d/wH

, where the square-root reduction factor

is due to the field enhancement at the (ﬂat) sam-

ple edge. Note that surface imperfections and creep

over the surface barrier reduce H

to smaller val-

ues,



d/wH

< H



d/wH

; at the same time

the macroscopic origin of the geometric barrier pre-

vents H

from dropping below the value



d/wH

Extending the above calculation for the current

and field profiles to the vortex penetrated sample

we can determine the magnetization; even in the

absence of bulk pinning we expect to find a hys-

teretic magnetization loop due to the presence of

the geometrical barrier. Following the rules defined

in Sect. 12.11.1 we split the sample into a current

free central vortex region with B

(|x| < x

) =0

and a vortex free edge regime with a Meissner cur-

rent J

< |x| < w)=(c/2)B

(x, 0) =0;corre-

spondingly the complex function § is real and imag-

inary in the two regions and we find the solution

§( = x +iz)=H

[(

−x

)/(

−w

)]

1/2

producing

the current and field profiles of the vortex penetrated

state

(|x| < x

)=0,

(|x| < x

, z =0)=H



− x

< |x| < w)=

|x|

2



− x

< |x| < w, z =0)=0.

(12.464)

The position x

of the vortexfront again follows from

balancing forces at the edge: the edge current (at

x ≈ w−d/2) shouldmatchtheforcerequired toover-

come the geometrical barrier,J

(w−d/2) ≈ cH

/2,

and hence

≈ w



1−H

. (12.465)

Upon increasing H

beyond H

vortices rush into

the sample and set up a dome-like field profile.

As the dome expands with field the magnetization

decreases M ≈ H

− x

)/8wd ≈ H

/8H

.At

≈ H

we have −4M ∼ H

≈ w−d/2andthe

system becomes reversible.Upon decreasing the field

from below H

the front x

first moves towards

theedgeandvorticesstartleavingthesamplewhen

≈ w − d/2. Decreasing H

from above H

vor-

tices leave the sample immediately. Note that while

vortices creep over surface barriers via half-loop for-

mation (cf. Sect. 12.11.1 above), vortex creep over

the macroscopic geometrical barriers would involve

segments of length ∼ d moving over distances of or-

der ∼ w and hence is strongly inhibited. Also, note

that imperfections easily destroy the surface barrier,

whilethe geometric barrier with its macroscopic ori-

gin is very robust.

12 Vortex Matter 615

12.12 Vortex Glasses

The presence of disorder turns the vortex lattice

into a glassy phase which is most conveniently de-

fined through its response: as the current j goes to

zero the barriers inhibiting vortex motion diverge,

U(j → 0) ∼ U

/j)



, and the vortex velocity

v ∝ exp[−U(j)/T]goestozeroinasingularman-

ner [15–17, 19–21]. The glass exponent  describ-

ing the divergence of the barriers is a characteristic

quantity of the phase.This should be contrasted with

the situation where the barriers saturate, produc-

ing a regular ohmic response with a finite resistiv-

ity 

TAFF

∼ 

exp[−U

/T](here,

= 

(B/H

)

denotes the ﬂux ﬂow resistivity).Such thermally ac-

tivated ﬂux ﬂow (TAFF) occurs in a pinned liquid

where the divergence of the activation barriers is

cut off by plastic rearrangements in the vortex sys-

tem [56].

A second characteristic of the glass phase is the

loss of translational order. Here, we have to distin-

guish between weak and strong disorder and be-

tween uncorrelated (due to point defects) and cor-

related disorder (e.g., due to columnar defects or

twin boundaries). Originally, the vortex-glass phase

has been conceived as a strongly disordered phase

where the lattice order has been largely destroyed

through the appearance of dislocations [16]. Further

analysis has shown, however, that the loss of trans-

lational order due to disorder is much more subtle:

within the elastic description outlined in Sect.12.9.4,

the asymptotic loss of order is only logarithmic,

u

(R)∼a

ln(R/R

) [19–21]. Hence a scattering

experiment would still produce algebraic peaks [21]

(as for a 2D lattice with quasi-long-range order, cf.

Sect. 12.7.4) and following this characteristic this

phase has been termed a Bragg-glass. Also, it has

been shown that for weak disorder and low magnetic

fields this Bragg-glass phase is stable with respect to

spontaneous creation of dislocations [21,451–453].

The other extreme is that of strong disorder due

to columnar defects.Contrary to uncorrelatedpoint-

like disorder which induces line wandering, corre-

lated disorder due to columnar tracks favors local-

ization of the linesonto thedefects.Upon irradiation,

theoriginal vortexlatticeis destroyedand thepinned

phase below the irreversibilityline turnsintoa glassy

phase which has been termed “Bose-glass” [55] in

analogy with the Bose-glass phase appearing in the

phase diagram of dirty 2D quantum bosons [454].

Besides these two “weak” and “strong” Bragg and

Bose-glass phases a third type of glass, the “origi-

nal” vortex-glass phase [15], is still much debated.

Quite interestingly, the Hamiltonian originally pro-

posed to describe the vortex-glass phase, when ana-

lyzed for the weak disorder case, has been shown to

produce Bragg-glass order [20,21]. The present sta-

tus of the (amorphous) vortex-glass phase is rather

vaguely defined: again due to point like disorder, the

latterisassumedtobestrongenoughtointroduce

line entanglement anda finite density of dislocations.

With dislocations present, the question then arises

whether this amorphous vortex-glass is a thermody-

namically distinct phase as compared to the vortex-

liquid [455]. Indeed, isolated dislocations still can

be described within an elastic theory and the com-

petition between elasticity and disorder produces a

glassy response for the individual dislocation line,

similar to the glassy response of an individual vor-

tex line [38,377,456].However, going to a finite den-

sity of dislocations the elastic description becomes

ill defined as the dislocations start interacting and

it is unclear whether the resulting phase turns into

a glass or a liquid phase. An interesting question

in this context is about the relation between struc-

tural order and stiffness (if such relation exists at

all): the analysis of the low-frequency response of a

collectively pinned vortex manifold (a vortex-glass

with a displacement field u

(R)∝R

2

and diverg-

ing barriers described through the random manifold

regime) gives a superﬂuid density 

(!) which van-

ishes ∝ [ln(1/!)]

−2/(2+d−2)

in the limit ! → 0

[457]. The question then is whether the quasi-long-

range-orderedBragg-glass(witha displacementfield

u

(R)∝ln(R/R

)) behaves differently and devel-

ops a finite superﬂuid stiffness.

Confronted with (possibly) three types of new

glass phases a number of questions arise: what are

their phase boundaries, what is the nature of the

transitions, and what are the neighboring phases.

Let us first concentrate on the Bragg-glass: Since

the effect of disorder is weak the Bragg-glass melts

616 G. Blatter and V.B. Geshkenbein

via a first-order transition into a vortex-liquid upon

increasing temperature, the melting line remaining

essentially unchanged as compared to the disorder

free case. Increasing the magnetic field the Bragg-

glass is expected to become unstable as well [21], cf.

Fig. 12.2. Magnetization experiments on anisotropic

[458–460] and layered [461, 462] material exhibit a

“second”pronouncedpeak suggesting a rapid change

in the pinning and/or creep characteristic of the

material as the magnetic field is increased. Muon

spin resonance and neutron scattering experiments

[162, 279, 463] provide evidence for a sudden loss

of order at higher values of magnetic field. Hence

increasing the magnetic field appears to produce a

disorder-driven crossover or transition into a more

strongly disordered phase, possibly characterized by

a finite density of dislocations and/or vortex en-

tanglement; numerical simulations [464–466] and

theoretical considerations [22,422,453,467] support

this expectation. The sharpness of the experimen-

tal signal as observed in layered BiSCCO and Nb

[462,468–470] suggests that indeed we deal with a

first-order phase transition.The resulting disordered

phase at high fields is either an amorphous vortex-

glass phase or a frozen liquid. In Sect. 12.12.1 below

we discuss how to locate the position of this disorder

induced transition via a Lindemann argument.

While point disorder disfavors the crystal through

forced line wandering, one expects that correlated

disorder with its tendency to localize vortices dis-

favors the vortex liquid. Irradiation with heavy ions

then not only transforms the (first-order) melting

line into a (second-order) Bose-glass line but also in-

duces an upward shift of the phase transition — we

will estimate the size of this shift with the help of a

modified Lindemann criterion in Sect. 12.12.1.

At low fields the transition into the Bragg-glass

phase upon cooling remains first-order: a small

amount of disorder does not destroy the first-order

melting transition. The jumps in magnetization and

entropy disappear at high fields [37, 471] and the

first-order line terminates, at least in continuous

anisotropic material such as YBCO — the question

then arises whether we deal with a critical endpoint

(implying that the vortex-glass and liquid phases are

no different) or possibly a multi-critical point with a

second-order transition continuing on and separat-

ing a vortex-glass phase from the vortex-liquid (cf.

Fig. 12.2). In looking for such a second order transi-

tion a scaling analysis of the transition line and the

analysis of criticalscaling in the vortex-glass and liq-

uid response are valuable tools in providing evidence

for the existence of a generic phase transition; the re-

sulting exponents characterize the transition. Below

we derive the scaling rules for the vortex-glass transi-

tion, see Sect. 12.12.2. Based on such a scaling analy-

sis the presence of a vortex-glass transition has been

inferred from transport data measured on epitaxial

thin films [35,472]. Early experiments on untwinned

single crystals defected by electron [473] and pro-

ton irradiation [474] failed to identify vortex-glass

scaling; however, increasing the (proton) irradiation

dose above a critical value, vortex-glass scaling has

been observed recently in an untwinned single crys-

tal [475].Thesame scaling analysishas been success-

fully carried out on twinned samples [476], thus pro-

viding evidence for a generic Bose–glass transition

and a Bose-glass phase in the presence of correlated

disorder.

12.12.1 Disorder-Induced Melting

We concentrate on low temperatures and consider a

vortex system subject to uncorrelated point-like dis-

order; the magnetic field is assumed parallel to the

axis of the anisotropic superconductor. At first sight

collective pinning theory tells that disorder is more

relevant at low fields: at low magnetic fields pinning

involves individual vortex lines, while increasing the

field the elastic forces gain in importance and at

high fields pinning involves 3D vortex bundles.How-

ever,when asking about lattice order we should com-

pare the disorder-induced mean squared displace-

ment amplitude u

(L) with a

= ¥

/B rather than

pinning and elastic energies.Starting from short dis-

tances, the individual vortex line first proceeds along

its pinning valley (u

(L < L

)∼

(L/L

)

)and

then wanders between different such valleys with a

superdiffusive behavior u

(L > L

)∼

(L/L

)

5/4

This wandering is limited by the presence of other

vortices — their repulsive interaction confining the

vortex line to its lattice site becomes relevant at dis-

12 Vortex Matter 617

tances L > "a

. However, if before reaching this

length the vortex line has wandered a distance c

away, the neighboring vortices cannot force the line

back to its lattice site and the lattice melts [22]. The

Lindemann condition for the disorder-induced melt-

ing then reads u

("a

)≈c

and produces the

melting field (cf. Fig. 12.2)

m,dis

≈



2c



8/3





5/3

, (12.466)

where we have assumed that pinning is not very

weak, L

< "a

or equivalently 2c

< 1.

Assuming a Lindemann number c

≈ 0.15 this re-

quires an extended single vortex pinning regime

≈ 0.15H

; assuming parameters for YBCO the

disorder-induced melting field B

m,dis

ends up in the

few Tesla regime.

A similar analysis can be carried out for layered

material such as BiSCCO [422].We consider the sim-

plest case where the layers are coupled electromag-

netically (" = 0); in thiscase the disorder spreads out

each vortex line into a tube of area u

, cf. (12.428).

The Lindemann criterion for the disorder-induced

melting transition takes the form u

≈ c

and we

obtain the melting field

m,dis

≈ 2c







1/2









(12.467)

Again,consistency requires that we can ignore the in-

teraction between pancake vortices in thesame layer:

comparing tilt and shear energies,

tilt

∼ E





, E

shear

∼ c

d , (12.468)

we obtain the condition

m,dis

< B











2c









1/2

< 1 . (12.469)

Thestrongpinningcondition (12.469) requiresa pin-

ning energy U

> 10

≈ T

; this condition is

roughly matched intypical crystals resultingin a dis-

order induced melting in the field range B

m,dis

∼ B



The above Lindemann estimates for the location

of the disorder induced transition are easily done; a

much harder question is to understand the nature of

the resulting disordered phase, in particular its en-

hanced pinning and reduced creep properties. The

most obvious interpretation of the sharp increase in

magnetization at B

m,dis

is in terms of a (roughly 10-

fold) increase in the critical current density [462].

However, the disorder-induced phase transition re-

quires itself strong pinning and the transition ends

up in the single pancake-vortex pinning regime;once

each pancake vortex is optimally pinned it is hard to

imagine how to enhance pinning further. Expand-

ing the search area u

≈ c

to a

for the optimal

accommodation of individual pancake vortices pro-

duces an increase in j

by a factor 1.5 at most. An

alternative explanation of the large jump in the mag-

netization is based on vortex creep: what is measured

in the magnetization experiment is not the critical

current density j

but the relaxed current density j(t)

after creep, cf. (12.302). Indeed, experiments on BiS-

CCO [477–479] show that the creep barriers diverge

faster in the disordered high-field phase.The appear-

ance of two vortex phases near the second magneti-

zation peak, an ordered low-field and a disordered

high-field phase, has recently been observed in fast

magneto-optic imaging [478, 480]. The two phases

are characterized by different current profiles sepa-

rated by a front [477,478]; the velocity of this front

separating the ordered and disordered phases goes

to zero with the magnetic field B approaching B

m,dis

Applying a field B below but close to B

m,dis

the ex-

pulsion of the disordered phase from the sample can

betracedonatimescaleofafewseconds,while

the dynamical establishing of the disordered phase

throughout the sample is observed when ramping

the field beyondB

m,dis

.The same type of ordered and

disordered phases have been discussed in the context

of dynamical effects associated with the peak effect

in NbSe

[468,469].Both,the sharpness of the transi-

tion [469] as well as the observation of supercooling

of the disordered phase [477] suggest a first-order

nature for this field-driven order-disorder transition.

618 G. Blatter and V.B. Geshkenbein

Melting in the Presence of Correlated Disorder

Strong correlated disorder not only transforms the

first-order melting line into a second-order Bose-

glass transition but also produces an upward shift in

the melting/irreversibility line [481]. This shift can

easily be derived with the help of a Lindemann anal-

ysis.

In a first step we reformulate the usual Linde-

mann criterion u



) ≈ c

into an equiv-

alent energy criterion: balancing the longitudinal

/L)andtransverse(c

(u/a

)

L) elastic ener-

gies we obtain the longitudinal length L ∼ "a

,and

equating the resulting elastic energy at the Linde-

mann displacement u ∼ c

to the thermal energy,

T ∼ "

/"a

, we obtain the criterion

∼ c

, (12.470)

telling us that the vortex system melts when the ther-

mal energy per unit length (T/"a

) becomes a (Lin-

demann) fraction of the confining potential energy

per unit length "

Let us use this energy criterion in order to esti-

mate the shift in the melting line due to columnar

disorder. Consider first the weak-field situation with

u



1/2

= c

> d

(we assume a

< ). We treat

the effect of disorder perturbatively: requiring the

temperature to be large, T > T

(cf. (12.445)), the

vortex lines are pinned collectively by the action of

many defects. Furthermore, the disorder energy is

small compared to the elastic energies at melting if

u



as given by (12.446)is larger than u



= c

as determined by the elastic forces, requiring that

T >

> T

. (12.471)

The presence of columnar defects within the po-

tential well leads to an effective lowering of the

thermal energy: The ﬂuctuating vortex line probing

the area c

is exposed to N

∼ c

compet-

ing defects. The latter produce the pinning energy



√

r

), where the last factor gives the rela-

tive contribution of each trap (cf.the estimate of the

pinning energy leading to (12.445)). The modified

Lindemann criterion reads

−



r

∼ c

, (12.472)

resulting in a Bose-glass line T

shifted to higher

temperatures as compared to the melting tempera-

ture T

in the unirradiated material,

− T

∼ 

r

∼

, (12.473)

where we have expressed the pinning energy 

through the depinning temperature T

(< T

), see

(12.441),in the last equation.The weak-pinning con-

dition (12.471) then tells us that the relative shift

− T

)/T

is small.

The above analysis is valid as long as the vortex

samples many traps within the potential well pro-

duced by its neighboring vortices. For high fields

< d

we have either none or of the order of one

trap available in each vortex potential well. We then

should expect the Bose-glass line to approach the

original melting line in a smooth way.The weak pin-

ning condition now requires comparison of u



given by (12.443)with c

and we obtain the weaker

condition T > T

. The mean energy lowering over

many vortices due to the presence of columnar traps

is given by 

)(r

r

), where the second

factor gives the probability to have a defect available

within the ﬂuctuation area c

, whereas the last fac-

tor gives the mean contribution of this defect. The

result (12.473) then is modified to take the form

− T

∼ 

r

∼





(12.474)

The shift is reduced by a factor∝

√

/B and T

(B)

approaches T

(B)atlargefields.

While the Lindemann criterion quite successfully

predicts the location of the melting line, one should

appreciate that the determination of its shift due to

disorder is a much more subtle question and a more

rigorous analysis should account for the change in

energy of both the solid and liquidphases. Neverthe-

less,the good agreement with experiments on irradi-

ated YBCO single crystals [481] lends some support

to the rough estimates given above.

12 Vortex Matter 619

12.12.2 Vortex-Glass Scaling

Inthepresenceofstrongenoughdisorderthefirst-

order melting transition is expected to transform

into a second-order glass transition. The existence

of such a generic phase transition can be traced with

the help of a scaling analysis as suggested by Koch

et al. [35], see also [16].Assuming a continuous glass

transitionat T

we can describe the emerging critical

behavior in terms of the diverging length and time

scales 

∝|T − T

−

and 

∝ 

,with and

z the correlation length and dynamical exponents.

Above the criticaldimension d

=6oftheglasstran-

sition these exponents take on the mean-field values

 =1/2andz = 4 [482] (these are the same char-

acteristics as for conventional spin glasses [483]),

while critical ﬂuctuations are expected to increase z

in lower dimensions [484].The characteristics of the

glass transition can be extracted from the current-j-

electric-field-E characteristic via the following scal-

ing analysis: Since the vector potential A scales as an

inverse length (this follows from gauge invariance),

the electric field E ∝ @

A is expected to scale like

1/



,hence E

1+z

is an appropriate scaling com-

bination. On the other hand, since j ∝ @

f ,withf

denoting the free energy density, the scaling com-

bination for the current density is j

d−1

. Collecting

results we can define the scaling Ansatz

E ∝ 

−(z+1)



j

d−1



. (12.475)

The Ansatz (12.475) is consistent with the one

obtained for the complex conductivity  (!) ≈



/(−i! + "): Since the superﬂuid density 

scales

with length according to 

∝ 

2−d

[485],weexpect a

scaling law for the complex conductivity of the form

 (!) ∝ 

2+z−d

(!

) ; (12.476)

equation (12.476) then provides additional informa-

tion on the frequency dependence of the response

near the glass transition [16, 486]. Here, we con-

centrate on the dc-response encoded in the scal-

ing Ansatz for the current-voltage characteristic

(12.475).

Above T

, we expect the response to be ohmic at

large scales L > 

.TheselargedistancesL > 

are probed with small current densities j < j

∝



1−d

,with the crossover current density j

vanishing

on approaching the transition temperature accord-

ing to

∝ (T − T

)

 (d−1)

. (12.477)

Within this ohmic regime the scaling function e

(x)

vanishes linearly in x, e

(x → 0) ∼ x,andweobtain

the scaling law for the resistivity in the form

(T) ∝ (T − T

)

 (z+2−d)

. (12.478)

Below T

, the system shows glassy response at large

scales L > 

, i.e., small current densities j < j

−

∝



1−d

, where again, the crossover current density j

−

scales according to

−

∝ (T

− T)

 (d−1)

. (12.479)

The scaling function e

−

takes the form e

−

(x → 0) ∼

exp(−a/x



) and we obtain the glassy characteristic

E ∝ exp



−c









. (12.480)

Approaching the transition at T

, the diverging

length scale 

in (12.475) has to cancel out and

hence e

(x →∞) ∼ x

with ˛ =(z +1)/(d −1);we

then obtain the power-law current-field characteris-

tic

E ∝ j

(z+1)/(d−1)

. (12.481)

Since z > 4isexpectedind = 3 [482], an expo-

nent ˛ > 2.5 is predicted. Right at the transition



∼∞and the power-law characteristic (12.481)

is valid on all scales, i.e., at arbitrary small current-

densities j. Moving away from the transition,

and

the crossover current-densities j

are finite and the

power-law (12.481) valid at small distances (L < 

)

and large current densities (j > j

) crosses over to

the ohmic (12.478) and glassy (12.480) characteris-

tics at large distances (L > 

) and small current-

densities (j < j

) for high and low temperatures,

respectively, see Fig. 12.36.

The above scaling analysis in fact applies to an

isotropic disordered superconductor, e.g., a gauge