Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

590 G. Blatter and V.B. Geshkenbein

opt

(F) ∼ L





1/(2−

d,n

)

opt

(F) ∼ 







d,n

/(2−

d,n

)

. (12.373)

Inserting the result for L

opt

(F) back into (12.372) we

obtain the creep barrier with its characteristic glassy

exponent ,

U(F)=U







,  =

2

d,n

+ d −2

2−

d,n

. (12.374)

When applying this general resultto the vortex lat-

tice we have to account for the modifications due to

the dispersive nature of the elastic moduli and the

anisotropic geometry of the superbundles. Within

the small bundle pinning regime, the bundle dimen-

sions along the field as well as along the direction

of the hop grow very fast, L

∼ R



∼ R

⊥

.Us-

ing the scaling behavior of R

⊥

with current density

j, R

⊥

(j) ∝ (j

/j)

1/(2−)

(this relation follows from bal-

ancing the elastic (shear) energy against the energy

gain from the driving Lorentz force), we obtain the

scaling laws L

∼ R



∝ (j

/j)

3/(2−)

for the bundle

dimensions in the field/forceplane.For intermediate

size bundles we have L

∼ R



∼ (R

⊥

/a

)

1/2

and

hence L

∼ R



∝ (j

/j)

3/2(2−)

. Finally,for large bun-

dles, L

∼ R



∼ (/a

⊥

and no additional scaling

factors arise. Summarizing, we have to modify the

result (12.374) within the small (and intermediate)

bundle pinning regime by changing the exponent 

(the correction terms follow from the additional ge-

ometry factor L



⊥

, cf. (12.368)),

 →  +

2−

, small bundles (12.375)

 →  +

2−

, intermediate bundles .

A further complication concerns the wandering ex-

ponent : Within the small bundle pinning regime,

the generalized Larkin–Ovchinnikov result (12.371)

for the displacement correlation function u

(R, L)

depends only logarithmically on the distances R and

L and hence the wandering exponent changes to

the new value  = 0 within the small bundle creep

regime. This reduced exponent remains also valid

within the intermediate bundle creep regime where

the transverse length R

⊥

due to the shear relaxation

in the subbundles is still smaller than the screening

length . We then arrive at the following exponents

 characterizing creep of vortex bundles within the

lattice pinning regime:

 =

, small bundles ,

< R

⊥

, R



∼ L

<  ,

 =1, intermediate bundles ,

< R

⊥

<  < R



∼ L

 ≈

, large bundles ,  < R

⊥

, R



∼ L

(12.376)

The above results are applicable within the random

manifold pinning regime where the typical hopping

distance u is less than the lattice constant a

of the

ﬂux line lattice. On the other hand, the relevant hop-

ping distance u can grow well beyond this value, e.g.,

by decreasing the current density j or in the context

of relaxation on large scales, implying a crossover

to the Bragg-glass (BG) scaling regime. Within this

regime, the wandering exponent  is again reduced

to zero and the exponent  takes the value

 =

, BG regime , R

< R

⊥

. (12.377)

In calculating the above creep exponents  we have

assumed wandering exponents  = 0 (small bun-

dles),  = 0 (intermediate bundles),  ≈ 1/5(large

bundles), and  = 0 in the BG creep regime.

We now are ready to collect the results describ-

ing creep at small driving forces j  j

.Letusas-

sume that the sample has been initially prepared in

a critical state belonging to the single vortex pin-

ning regime, i.e., L

< a

(note that we use the line

wandering exponent 

1,2

=3/5 rather than the re-

sult 

1,2

≈ 5/8 derived from numerical simulations

and used in Sect. 12.9.4 above). As the current j de-

cays due to creep, the activation barrier U(j )evolves

according to the following scheme:

12 Vortex Matter 591

U(j) ≈

⎧

⎪

⎨

⎪

⎩





1/7

, j

< j  j





5/2

, j

< j < j

, j

< j < j





7/9

, j

< j < j





1/2

, 0 < j < j

(12.378)

with U

≈ U

)

1/5

, U

≈ U

(/a

)

5/3

≈ U

(/a

)

4/3

, U

≈ U

/

)

7/5

; j

≈

)

7/5

, j

≈ j

/)

2/3

, j

≈ j

/)

4/3

≈ j

(

)

9/5

. The time decay of the current

density followstriviallyfromcombining (12.302)and

(12.378) and solving for j. The various creep regimes

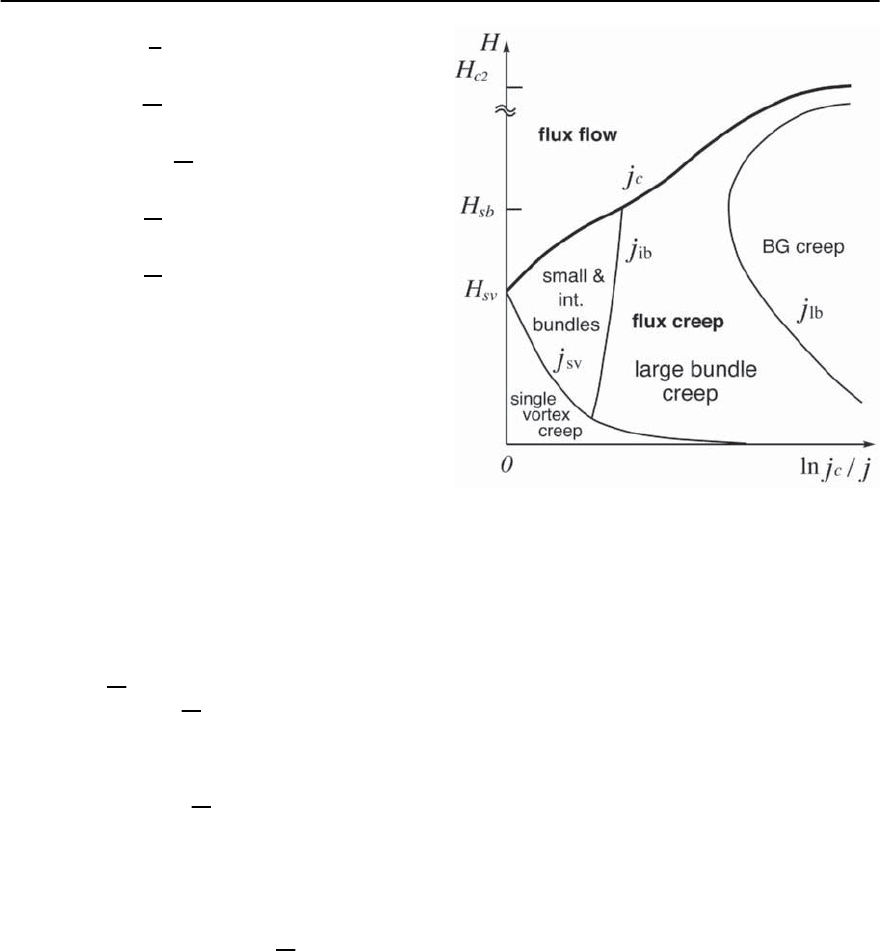
are illustrated in Fig. 12.28.

Again we adda note on anisotropic materials mak-

ing use of our scaling rules (12.170); basically, the

scaling approach is limited to length scales R



< ,

however, one can show [150] that the results can be

extended to the larger regime R



< /".Weas-

sume a current density j directed along the planes,

j ⊥ H and have the vortex system start decaying

from the single vortex pinning regime such that

< "a

√

. As the current density j drops be-

low j

(# , B) ≈ j

(

√

/"a

)

7/5

(for 

1,2

≈ 5/8

the exponent is 11/8), we enter the vortex bundle

creep regime where the activation barrier increases

rapidly, U(# , j, B) ≈ U

(# , B)[j

(# , B)/j]

5/2

,with

(# , B) ≈ U

("a

√

)

1/5

,obtainedbyrequir-

ing continuity across the boundary between the

single vortex and the lattice pinning regimes. The

boundary j

(# , B), within which the scaling the-

ory can be applied, is found by rescaling the con-

dition R



) ≈ a

)

3/2

∼ /",andweob-

tain j

(# , B) ∼ j

(# , B)("a

√

)

2/3

.Notethat

is larger than the current density j

limiting the

small/intermediatebundlepinning regime.Fora cur-

rent density j directed along the y



axis (out-of-plane

current) the creep motion is directed along the su-

perconducting planes and we have to substitute the

in-plane current density ratio j

/j by its out-of-

plane counterpart "

/j. The extension of the creep

Fig. 12.28. Creep regimes and their relative position within

the B–j plane. Disorder is irrelevant in the ﬂux-ﬂow regime

at large fields and large current densities.Vortices move via

creep in the low-field-low-current region below the criti-

cal current density j

(B). The ﬂux creep regime is divided

up into a single-vortex creep regime at large current densi-

ties,followed by the small to intermediate and large bundle

creep regimes at lower current densities (larger fields). At

very low current densities we enter the BG creep regime

analysis to anisotropic materials beyond the scaling

regime is rather tedious and we refer the reader to

the original literature [150].

Quantum Creep

Abovewehaveanalyzedthedecayofavortexden-

sity gradient due to thermal activation of the vor-

tices out of their metastable states. According to this

classical picture the decay rate (12.365) should van-

ish in the zero temperature limit. However, one may

expect that quantum ﬂuctuations trigger a decay

of the critical state via quantum tunneling at low

temperatures, leading to a saturation of the decay

rate S =dlnj /dlnt. Indeed, such a saturation has

been observed in a number of experiments on oxide

superconductors [50, 52, 388], as well as in Chevrel

592 G. Blatter and V.B. Geshkenbein

phase [389], organic[390] and heavy fermion super-

conductors [391].

Macroscopic quantum phenomena have always at-

tracted much interest as they naturally touch the

boundary between quantum and classical physics:

macroscopic systems are coupled to their environ-

ment and thus are inherently dissipative. The clas-

sic and most carefully studied system exhibiting

macroscopic quantum tunneling is the (rf) super-

conducting quantum interference device (SQUID)

[149, 392–395]. In particular, Caldeira and Leggett

[149] have discussed in detail how to extend the

quantum description to macroscopic systems, the

main effect of the dissipative environment being to

suppress the probability for the tunneling process.

Later, this early work has been extended to vortex

motion by quantum tunneling in Josephson junction

arrays [396], thin (disordered) films [397–399], and

bulk superconductors[400,401].

The decay of a metastable state due to tunneling

is similar to the classical decay process via thermal

activation; the additional feature to be taken care of

in a tunneling process is the time component of the

motion. During tunneling the vortex moves under

the barrier, hence the process is forbidden (virtual)

and the longer the time the string spends under the

barrier, the less chances there are for the process to

happen (for the thermally activated situation time is

irrelevant as the vortex hops over the energy barrier

in a real process). While for an activated motion the

probability is determined by the saddle-point solu-

tion of the free energy (12.313), one has to find the

saddle-point solution of the Euclidean action in or-

der to describe a tunneling event [149,402–406]. The

quantum problem then is a d +1-dimensionalgen-

eralization of the d-dimensional classical problem,

where d denotes again the dimension of the object,

e.g., d = 1 for the vortex line.

As discussed in Sect.12.3.2 above,the vortex equa-

tion of motion involves transverse (Hall) and dissi-

pative forces, see (12.45),

˙v

+ 

+ ˛

∧ˆz = f

ext

. (12.379)

Here, we include an additional massive term m

˙v

with the motivation that the quantum tunneling of

a massive object is the most simple case to analyze.

Expanding the dynamical coefficients in (12.45) it is

possible to derive a vortex mass (see also [407,408],

where an electronic vortex mass m

≈ (2/

has been found, and [409,410] reporting a mass en-

hanced by a factor (k

)

in a superclean material;

besides the electronic contribution, a second term

=(¥

/4c)

of electromagnetic origin con-

tributesto the vortex mass [407];in a tunnel junction

this result is modified to m

∼ C¥

/

with C

the junctioncapacitance and 

the size of the phase

core, typically m

 m

), however,it turns out that

in a bulk superconductor the dissipative and Hall

termsalwaysdominateoverthemassterm,thedis-

sipative contribution being the most relevant one in

dirty and clean materials while the Hall term domi-

nates in the superclean limit.In the following,we first

discuss the simple and illustrative case of tunneling

of a massive string and then proceed with the analy-

sis of vortex tunneling,discussing the dissipative and

Hall tunneling in sequence.

The Lagrangian generating the classical equation

of motion for a massive elastic string is







− F





, (12.380)

with the free energy functional F[u]givenby

(12.313). The displacement vector u(z, t)playsthe

role of the macroscopic variable.

Substituting t → −it in (12.380) we obtain the

(imaginary time) Euclidean action [405,406],







+ F







, (12.381)

for which we have to find the saddle-point solution.

The saddle-point solution is given by the classical

bounce trajectory where the string moves through

the inverted potential and bounces back to the ori-

gin, see Fig. 12.29 for a sketch illustrating the tunnel-

ing trajectory of a particle. Here, we are interested

in the scale for the action, i.e., we wish to determine

the quantity corresponding to U

,andthuswesetthe

driving force equal to zero, j = 0. Equation (12.381)

then has to be minimized with respect to the form

(length L and displacement u)andthedurationt of

the bounce and we will do this on the level of scal-

ing estimates. At this point we should note that the

12 Vortex Matter 593

Fig. 12.29. The tunneling trajectory (bounce, dotted line,

massive dynamics) is found as the classical solution of the

equation of motion in the inverted potential. In the dissi-

pative situation energy is transferred from the system to

the reservoir (dashed line)

tunneling process involves the same initial and final

states as encountered above in the determination of

the classical creep rate; the additional new feature

in the quantum problem is the relevance of the time

evolution of the vortex motion. In fact, the determi-

nation of the optimal geometry for the bounce so-

lution involves only the free energy part of (12.381)

and the result in the form of the collective pinning

length L

has been found above (12.325); the dis-

placement u ∼  is given by the disorder landscape.

Theestimateforthetunnelingtimet

is obtained by

equating the elastic and the kinetic energy densities,

(/t

)

∼ "

(/L

)

∼





1/2



∼



∼

√





(12.382)

wherewehaveinsertedtheresultt

into (12.381) in

order to find the minimal action for the tunneling

process in the last equation.In the limit of vanishing

dissipation the action does not depend on the collec-

tive pinning length L

and hence is independent of

the pinning potential.

Let us then apply these ideas to vortex tunnel-

ing. In accounting for the dissipative environment

we restrict ourselves to the simplest case of ohmic

dissipation with the viscous drag coefficient (12.45).

The corresponding dynamical term in the vortex ac-

tion can be obtained by coupling the system to a bath

of harmonic oscillators and subsequent integration

over the environmental (bath) variables [149],



4









u(z, t)−u(z, t



)

t − t





(12.383)

The expression (12.383) is nonlocal in time and we

transform to Fourier space to obtain the effective ac-

tion,

eff



2



2

(12.384)







|!| + "



|u(q, !)|

+ 

(q, u)



Equating the dynamical and elastic energy densities,



∼ "

,withq

∼ 1/L

the inverse length

of the tunneling segment,we find the tunneling time

∼ 1/!

and the corresponding action,

∼



, (12.385)

eff



∼







∼











1/2

∼





1/2

with L

given by (12.327). Here, we have introduced

the dimensionless parameter Qu =(e

/)(

/)

quantifying the strength of quantum ﬂuctuations

and playing the role analogousto the Ginzburg num-

ber in the context of thermal ﬂuctuations. For an

anisotropic material we have to substitute L

→ L

and hence S

eff

= "

4/3

eff,iso

The normalized creep rate S near j

takes the form,

S =

dlnj

dlnt

≈ −



eff

. (12.386)

The main parameter determining the action and the

tunneling rate is the ratio 

/.Asmallactionfavor-

ing tunneling is obtained in materials characterized

by a large normal state resistivity 

and a small co-

herence length  . The quantum unit of resistance is

594 G. Blatter and V.B. Geshkenbein

/e

≈ 4.1k§, thus the phenomenon of quantum

creep should become experimentally observable for

ratios 

/ ≥ 1k§.The result (12.386) depends only

weakly on the disorder potential via a square root de-

pendence on the critical current density j

Finally, let us discuss the case of a Hall-type vor-

tex dynamics as it is relevant in a superclean su-

perconductor (cf. Sect. 12.3.2; the Hall dynamics is

also relevant for the tunneling of vortices in super-

ﬂuid He [411]). Substituting the dissipative dynami-

cal term 

|!|u

by the Hall term ˛

in the action

for the tunneling process and proceeding with scal-

ing estimates we immediately reproduce the result

(12.386) above but with 

replaced by ˛



∼





∼ n





1/2

. (12.387)

However, there is a lot of additional interesting

physics associated with the Hall tunneling of vor-

tices [412, 413]. In particular, the geometry of the

bounce solution is very different from that found in

the massive or in the dissipative situation. In the fol-

lowing, we discuss a model calculation which high-

lights the important differences and which also is

relevant for the tunneling motion of a (collectively)

pinned vortex. We concentrate on the 2D situation,

describing a vortex in a thin film (of thickness d)or

a pancake vortex in a strongly layered superconduc-

tor, see Sect. 12.5.3. Rewriting the external force f

ext

in (12.379) in terms of a potential U (R)theequation

of motion reads

∧ˆz =−∇U(R) , (12.388)

with ˛

= ˛

d = ¥

nd/c (see (12.45)). Equation

(12.388) is the equation of motion of a charged

(e) particle with zero mass in a magnetic field

B =(0, 0, ˛

c/e). Such a particle always follows

the equipotential lines defined by the potential U,

v = ∇U ∧ˆz/˛

. Expressing (12.388) in components

we obtain the set of equations

@U (x, y)

, ˛

=−

@U (x, y)

(12.389)

The action producing these equations of motion is





y˙x − U (x, y)



, (12.390)

where the first term is just the Lagrangian j · A/c

of a charged particle moving in a magnetic field B

produced by the vector potential A =(By, 0, 0). The

set of dynamical equations (12.389) is of the Hamil-

tonian form (see also [411,414] where the same ap-

proach has been used in the calculation of vortex tun-

neling in a superﬂuid and for particle tunneling in

the presence of a strong magnetic field): if we define

the coordinateq =

√

x,the momentum p =

√

and the Hamiltonian H(q, p)=U(x, y)wefindthat

the set (12.389) is equivalent to the canonical equa-

tions

@H(q, p)

=−

@H(q, p)

. (12.391)

The Hamilton equations (12.391) describe a parti-

cle moving in one dimension with a dynamics de-

fined by the y dependence of the potential U(x, y).

The coordinates x and y play the role of canonical

variables and we can immediately quantize the the-

ory by imposing the commutation relation [x, y]=

(1/˛

)[q, p]=i/˛

=i/nd.

An alternative way to go over to a quantum de-

scription starts from the action (12.390): In order

to describe the tunneling motion of the vortex we

have to go over to an imaginary time formalism.

However, a mere substitution t → −it in (12.390)

as done previously leads us to an action describing

aparticlemovinginanimaginarymagneticfield

(only one time derivative appears in the dynamical

part of (12.390)). On the other hand, if we perform

a simultaneous rotation of both the time t and the

y-axis, t → −it and y → iy,thedynamicaltermin

(12.390) becomes real again;in addition,ifthe poten-

tial U (x, y)iseveninthecoordinatey we recover a

real Lagrangian. Finding a saddle-point of the orig-

inal action describing the decay of the metastable

state then becomes equivalent to solving a real clas-

sical problem. In fact, this scheme for obtaining the

desired saddle-point solution can be put on more

firm grounds by exploiting the equivalence between

the original 2D Hall problem and the 1D Hamilto-

nian problem: we assume that the original poten-

tial U(x, y) can be rewritten in a form U(x, y)=

(f /2)y

(x),then the resulting 1D-problem is that

12 Vortex Matter 595

of a massive particle (with mass m = ˛

/f )moving

in a potential U

(q/

√

) ≡ U

(q) (note that close

to a (local) minimum we can expand any potential

U(x, y) into this form if we choose the appropriate

axes). Writing down the action for the 1D-particle

problem and going over to the imaginary time for-

malism we obtain the Euclidean action (t → −it)

=−iS(t → −it)=





˙q

+ U

(q)







p ˙q − H

(q, p)



, (12.392)

with the definitionH

(q, p)=p

/2m − U

.The usual

Wick rotation within the Lagrangian formalism is

equivalent to the combined rotation t → −it and

p → ip in the Hamiltonian formalism as the substi-

tution t → −it implies p → ip ; equivalently, we can

invert the potential U

(q) → −U

(q).

Returning to the original Hall-tunneling problem

in 2D we can set up the appropriate rule to go from

the action (12.390) to the imaginary time expression

.Remembering that the y coordinate plays the role

of the momentum p in the 1D Hamiltonian problem

we obtain the Euclidean action(assuming a potential

U(x, y)=(f /2)y

+ U

(x))

=−iS(t → −it, y → iy)





y ˙x −

+ U

(x)



. (12.393)

According to the above rule we should only invert

the potential along the x-axis, U

→ −U

;thispar-

tial inversion is crucial forobtaining the appropriate

“bounce”solution for the tunneling action.

ApotentialU(x, y) describing a tunneling situ-

ation should exhibit a local minimum (say at the

origin) and a connection via a saddle to free space

along one direction (the x-axis); we choose the form

U(x, y)=U

/

+ x

/

− x

/

] with the pa-

rameters U

and  describing a weak pinning sit-

uation, cf. Fig. 12.30. The Hall-tunneling problem

maps to the 1D-particle problem with a particle

mass m = ˛



/2U

in the cubic potential U(q)=

[(q/

√

)

−(q/

√

)

]. Using the exact solu-

tion for the tunneling action of a massive particle in

a cubic potential [149] and transforming this result

back to the Hall problem we obtain the final result





nd

. (12.394)

The result (12.394) does not depend on the depth of

the pinning potential but only on its geometry. This

can be readily understood if we consider the shape

of the “bounce”solution.Inverting the x-component

in U(x, y) we obtain an inverted potential with the

minimum and the saddle interchanged, cf. Fig. 12.30.

The trajectory describing the escape of the parti-

cle out of its metastable state follows the equipo-

tential lines in the inverted potential and describes

a circle-shaped curve of radius ∼ . The resulting

action S =2



dqp → ˛



dxy is a consequence

of the “geometrical” quantization and is solely de-

termined by the encircled area without any further

dependence on the depth of the potential, in agree-

ment with the result (12.394). The generalization of

this result to three dimensions (tunneling of a vor-

tex line) is straightforward: The area enclosed by the

trajectory simply has to be replaced by the enclosed

volume, S

/ =(˛

/)V = nV. Within the frame-

work of collective pinning theory (where a vortex

line segment of length L

tunnels by a distance ∼ )

we immediately reproduce the result (12.387). The

general situation including both dissipative and Hall

terms is discussed in [150].

A second illustrative example of a Hall tunneling

event is the depinning of a pancake vortex from a

trap, which is equivalent to the tunneling of an elec-

tron in the“classic”Hall problem (e.g.,out of adefect-

induced trap within the 2D electron gas to the edge

of the Hall bar). We choose a potential of the form

U(x, y)=U

(



+ y

)−Fx with a narrow symmet-

ric trap potential U

() increasing monotonously

from U

(0) = 0 to U

(∞)=U

within a distance

 = a. The applied force F is assumed to be small,

Fa  U

. The inversion y → iy of the trap potential

turns circular equipotential lines U

(x, y) = const.

into hyperbolas x

− y

=const., cf. Fig. 12.31. The

tunneling trajectory then forms a triangle CAA’with

the distances CB ≈ U

/F and AA’ ≈ 2U

/F deter-

mined by the depth U

of the trapping potential and

the applied force F.TheareaA ≈ (U

/F)

encircled

by the tunneling trajectory then determines the Eu-

clidean action S

/ ≈ ˛

/F)

[415].

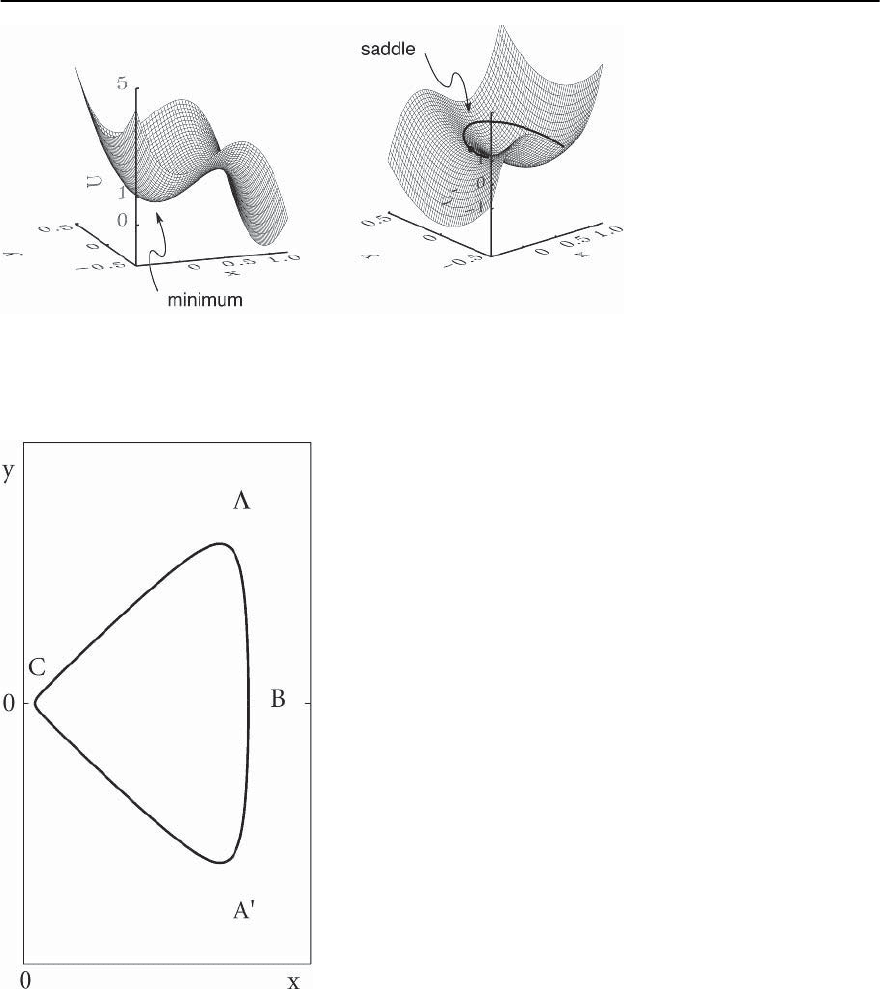
596 G. Blatter and V.B. Geshkenbein

Fig. 12.30. Metastable potential U =(27/4)[x

− x

+ y

](left) and its inversion U

=(27/4)[−x

+ x

+ y

](right). A

particle trapped in the minimum at the origin escapes via Hall tunneling out of its metastable state along an equipotential

line, ˛

v = ∇

⊥

,with∇

⊥

=(@

, −@

). The Hall tunneling trajectory starts from the saddle point (obtained from the

minimum after inversion) and follows the U

= 0 equipotential line shown in the plot

Fig. 12.31. Quasiclassical trajectory describing the Hall tun-

neling of a particle out of a metastable state

As with classical creep, the discussion of quantum

creep can be extended to vortex bundles and to low

current densities: extending the scaling analysis for

an isotropic medium from classical to (dissipative)

quantum creep one easily finds the relevant tunnel-

ing time  ∼ u

/U and the creep action S(j) ∼

/j)



with the exponent 

=(d +2)/(2 − )

and S

∼ 

(the same result is found within a

quantum dynamical FRG scheme (taken from un-

published work by D.A. Gorokhov, D.S. Fisher and

G. Blatter); note the exponent 

differs from the in-

correct expression quoted in [150]).

12.9.5 Thermal Depinning

Thehigh-T

superconductorscan be operatedathigh

temperatures where thermal ﬂuctuations of the vor-

tex lines are important. We distinguish between two

types of thermal motion: The large intervalley ﬂuc-

tuations producing ﬂux creep have been discussed

in Sects. 12.8.4 and 12.9.4 above. Here, we concen-

trate on (phonon-like) small-amplitude ﬂuctuations

restricted to the individual pinning valleys (intraval-

ley ﬂuctuations) which lead to a smoothing of the

pinning potential,reducing the pinning strength and

the critical current density while increasing the creep

barrier. Early studies of this phenomenon have been

based on the dynamical approach [23]; here, we

follow the simpler analysis using scaling estimates

and providing the same results [38, 417]. We first

discuss the interplay between thermal ﬂuctuations

and quenched disorder in the single vortex pinning

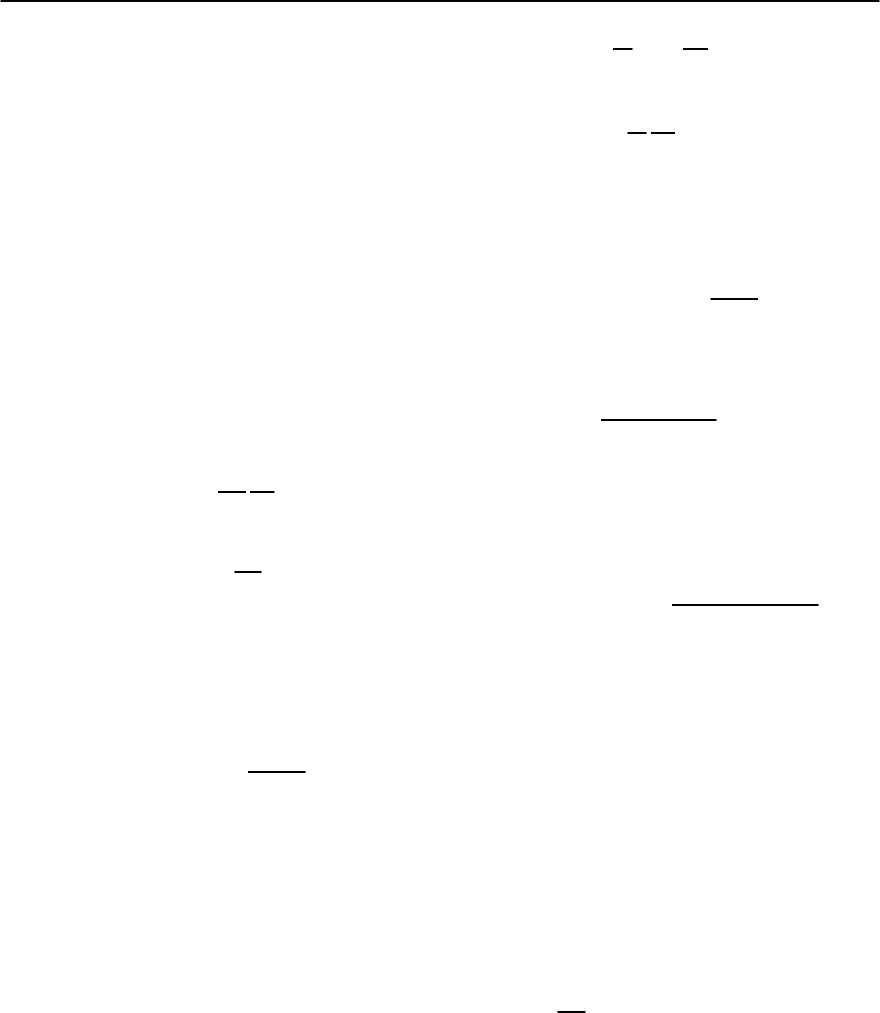
12 Vortex Matter 597

regimeand then extend the discussion to pinned vor-

tex bundles.

The key quantity entering the discussion of ther-

mal depinning is the mean squared thermal displace-

ment u

(L, t)

= [u(L, t)−u(0, 0)]



.Asim-

ple scaling analysis tells us that an individual vor-

tex line exhibits diffusive motion under the action

of (long-wavelength) thermal ﬂuctuations: the mean

squared displacement u

(L, t =0)

∼ (T/"

) L

diverges at large distances L →∞and, relating

length to time for a dissipative dynamics (cf.(12.51)),

t ∼ (

, we find the time-domain diffusion

in the form u

(L =0, t)

∼ T(t/

)

1/2

.More

rigorously, these results follow from the ﬂuctuation-

dissipation theorem [416] relating the mean squared

displacement u

(L, t)

to the single vortex Green’s

function G(q, !) (see (12.51)),

u

(L, t)

=2



2

(12.395)

× [1 − cos(qL − !t)]

× ctgh

!

Im G(q, !) .

Inthepresenceofdisorderwehavetocuttheq-

integration in (12.396) on the inverse (temperature

dependent) pinning length 1/L

(T), leading to the

finite result

u

(T), t →∞)

∼

(T)

. (12.396)

Thermal ﬂuctuations lead to a smoothing of the

quenched disorder potential: Due to thermal mo-

tion of the vortex line the vortex core will sample

the disorder potential over an extended spatial re-

gion∼u

(T))

.Asthe amplitude of the thermal

ﬂuctuations increases beyond the vortex core radius,

u

(T))

> 

, the vortex will experience an av-

eraged disorder potential and thereby pinning will be

reduced. Let us calculate the mean squared pinning

potential in the presence of thermal ﬂuctuations.Be-

fore taking the average over the disorder potential

(see (12.310))we perform a time average over vortex

positions,

E

(L)

≡





×

[z, u(z, t)] 



, u(z



, t



)]

= L







×[|u(0, t)−u(0, t



)|] . (12.397)

Transforming to Fourier space and assuming Gaus-

sian ﬂuctuations we obtain

E

(T))

 = L

(T)



(2)

(12.398)

× K(K)e

−K

u

(T),t→∞)

∼ L

(T)

⎧

⎪

⎨

⎪

⎩

K(u =0), u



 



uK(u)

u

(T))

n/2

, 

u



and using K(u =0)∼ 

,  ≡



uK(u) ∼ 

we can interpolate

E

(T))

∼ L

(T)

(12.399)





+ u

(T))



n/2

(at high temperatures where u



> 

the cutoff

on the K-integration is due to the “Debye–Waller”

factor exp[−K

u

(T))

/2] while it is due to the

correlator K(K)= |p

at low temperatures).

Finally, we have to determine the temperature de-

pendent collective pinning length L

(T). For n =1

(e.g., a vortex line trapped in between the supercon-

ducting planes of a layered superconductor or con-

fined to the plane of a thin crystal [418]) our scal-

ing estimates work fine and equating the pinning

energy (12.400) to the elastic and thermal energies

u

(T))

(T) ∼ T we obtain the collective

pinning length

(T) ∼ L





, T

=("



)

1/3

∼ U

, (n =1).

(12.400)

Notethat the depinning temperatureT

isitself tem-

perature dependent through the dependence of the

parameters "

,  ,and on 1 − T/T

.Theboundary

598 G. Blatter and V.B. Geshkenbein

dp,0

beyond which thermal smoothing becomes rel-

evant is determined from a solution of the equation

dp,0

= T

dp,0

) , (12.401)

with T

(T)=T

(0)(1 − T/T

)

; for ıT

-pinning

in high-T

superconductors, ˛ =1/3 [150]. The

temperature dependent activation energy becomes

(T > T

) ∼ T and the depinning critical current

density decays with increasing temperature accord-

ing to j

(T) ∼ j

(/L

)

/T)

[377,419].

For n =2thelengthL

(T) drops out of the scaling

analysis due to the marginal relevance of the disor-

der for the 1 + 2-dimensional single vortex problem

— the situation is similar to that encountered in the

dispersive pinning regime discussed in Sect. 12.9.3

above. Again, we can resort to perturbation theory,

starting from the thermal result and expanding in

powers of the disorder parameter  . To lowest order

the result reads [367]

u

(L) =

nTL



(4)

n/2

(4 − n)

(12.402)







n/2

1−n/2



with  ≡



uK(u) ≈ 

and where ...

denotes the average over thermal and quenched

disorder [note the modified dimensionality [ ]=

Energy

−(1+n)

,cf.(12.309)].Forn < 2thedisorder-

induced ﬂuctuations grow faster and dominate for

L > T





, in agreement with (12.400). For

n = 2 we can extract the depinning temperature

=("

)

1/3

, however, in order to find the pin-

ning length L

(T) we have to push the expansion one

term further; the result takes the form ( denotes a

longitudinal short scale cutoff)

u

(L) =

2TL



8



16



ln(L)



(12.403)

Equating the two correction terms we find an ex-

pression for the temperature dependent collective

pinning length, L

(T) ≈ L

exp[C (T/T

)

], with C

a constant of order unity which cannot be deter-

mined within the present perturbative approach, a

consequence of the marginality of the problem. Us-

ing functionalrenormalizationgroup theory the col-

lective pinning length is defined as the length scale

where the amplitude of the renormalized disorder

correlator K

appears to diverge, a scheme which al-

lows for the determination of the constant C in the

exponent [367]. For a short-range correlated poten-

tial the final result reads

(T) ∼ L

exp









, (n =2),

=("

)

1/3

∼ ("



)

1/3

(12.404)

∼ U

∼





1/2

Note, that the temperature dependence of the pref-

actor remains undetermined. For temperatures T >

thermal ﬂuctuations are large, the pinning en-

ergy follows the temperature,and the critical current

density decays rapidly

(T) ∼ T , j

(T) ∼ j

exp



−









(12.405)

These results are modified when the correlations

in the disorder potential are not short-ranged. In-

deed, the slowly decaying form factor of the vortex

core produces a non-integrable correlator (12.311)

K(u) ∼ K(0)(/u)

ln(u/) and the result (12.405)

is only reached at higher temperatures ln() T

;in

theintermediateregimeT

< T < ln() T

the

pinning length L

(T) grows with a simple exponen-

tial law L

(T) ∼ L

exp[CT/T

] [420]. Note, that

the large scale wandering exponent does not change

with this modestly longer range of the correlator.

At low temperatures T < T

dp,0

the above results

smoothly cross over to the corresponding zero tem-

perature expressions derived in 12.9.2.However,note

that the rapid increase of the pinning length L

(T)

with temperature sharply limits the single vortex

pinning regime and hence the applicability of the

results (12.405): using the condition L

(T) < a

find that the single vortex pinning regime extends up

to temperatures (cf. (12.328))

T < T

dp,0

. (12.406)

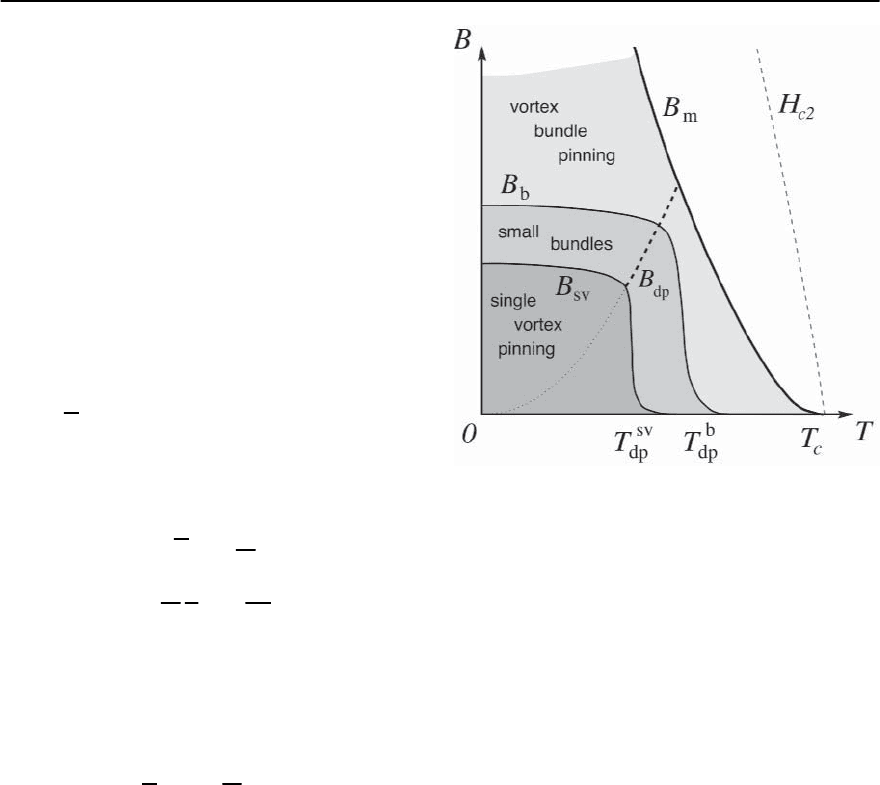
12 Vortex Matter 599

The thermal depinning of vortex bundles is an-

alyzedincloseanalogytothecaseofsinglevor-

tex pinning. Again we have to determine the mean

squared thermal displacement amplitude and use

the result in the determination of the renormal-

ized pinning energy. Here, the discussion is consid-

erably simplified due to the finiteness of the mean

squared thermal displacement u

(t →∞)

the amplitude u

(r, t)

saturates on scales r ≈ a

t ≈ a

(such a separation of scales is absent

in d =1, 2 where thermal ﬂuctuations produce a

divergent u



, which then has to be cut off by the

pinning length introduced via the quenched disorder

potential, cf. (12.396)).

The mean squared thermal displacement ampli-

tude has been calculated in Sect. 12.7.2, u



≈

√

"

. Thermal smoothing is relevant as soon

as the amplitude u



1/2

grows beyond the core ra-

dius , and using the definition u



) ≡ 

find the depinning temperature

√

"







1/2

∼





1/2





1/2

. (12.407)

Note that the right hand side of (12.407) does not

depend on temperature; in YBCO the parameter

Gi j

T=0

is of order unity and we find that the

depinning line in the H–T phase diagram,

∼

Gi B





, (12.408)

increases much steeper with temperature than in

conventional superconductors, emphasizing the im-

portant role of thermal ﬂuctuations in the high

temperature superconductors. Also, the expression

(12.407) for the depinning temperature of the vortex

lattice crosses over to the result (12.405) for the sin-

gle vortex depinning temperature as the field B drops

below B

, see Fig. 12.32.

The depinning line B

in Fig. 12.32 marks the

crossover to the thermallysmoothedpinning regime.

In order to have the first-order melting line survive

in the presence of disorder, pinning should be weak,

i.e., the melting line should stay away from the 1D

Fig. 12.32. Pinning regimes and their relative position

within the B–T plane. The single-vortex pinning regime is

boundedbyB

andby thesingle-vortexdepinning temper-

ature T

; all quantities within this regime are independent

of field. The small bundle pinning regime is limited by B

and T

; dependencies on field and temperature are expo-

nential. The large bundle pinning regime is characterized

by algebraic dependences on T and on B. The crossover

lines B

(T)andB

(T) drop rapidly beyond the depinning

line B

(T) (extrapolated to zero with the dotted line)

pinning regime. In anisotropic material the depin-

ning line crosses the melting line at H

∗

≈ 8GiH

and the single vortex pinning regime remains below

the melting line if B

) > H

∗

. In estimating the

position of the single vortex depinning temperature

we may distinguish between a weak pinning ma-

terial with T

∼ [j

Gi]

1/2

 T

(cf. (12.405))

and a more strongly defected material where T

ap-

proaches T

[150].In the latter case we have to solve

self-consistently for T

dp,0

;forıT

pinning in high-T

material we find

dp,0

≈ T



1−(j

(0)Gi/j

(0))

3/2



. (12.409)

Typical values for YBCO are B

≈ 6T,B

≈ 10

T, T

dp,0

≈ 60 K, H

∗

≈ 10T,andB

) ≈ 25 T,

telling us that a specific sample can belong to either

class of weakly or strongly pinning material (we have