Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.


560 G. Blatter and V.B. Geshkenbein
J) subject to a symmetry breaking field ∝ cos[m#
R
]
(here, #
R
denotes the angle of the spin at the posi-
tion R, m is an integer), where the BKT transition at
T
BKT
= J/2 competeswith theunlocking or“rough-
ening” transition at T
R
=8J/m
2
[255]. A simi-
lar scenario shows up in the context of the adsorp-
tion of a 2D crystal (elasticity C, lattice constant a)
on a commensurate substrate (lattice constant a/m),
where thedislocation-mediated melting transition at
T
m
= Ca
2
/4 competes with the roughening transi-
tion at T
R
=4Ca
2
/m
2
[305] (in both cases the ratio
between the two transition temperatures involves the
factor 16/m
2
; for m = 1 this is twice larger than in
the present layered situation).
Quite interestingly, proper modification of the Lin-
demann estimate (12.230) accurately reproduces the
two transition lines: replacing the logarithm in
(12.229) by the numerical ˛
L
= 1 produces the loop
transition at
B
em
dc
= B
"
0
d
T
ln
a
0
d
1−
T
4"
0
d
; (12.261)
accounting for the renormalization of the superfluid
stiffness, we find that B
em
dc
correctly extrapolates to
vanish at T =8T
BKT
.On the other hand,replacing the
logarithm by ˛
def
= 8 reproduces the result (12.258).
12.7.6 Characteristics of First-Order Melting
The mean-field transition at the upper critical field
H
c
2
(T) is of second order: the U(1) symmetry of the
complex superconducting order parameter ¦ forbids
the cubic term in the Landau expansion and hence
|¦ | is coming up smoothly from zero upon cooling.
However, thermal fluctuations turn this transition
into a crossover where Cooper pairs form,establish-
ing a finitelocal order parameter and a finite density
|¦ |
2
but without establishing any long-range order;
no symmetry is broken in this vortex liquid phase
which is no different from the normal metallic one.
The true transition into the superconducting state
then changes its nature and is shifted to the vortex
melting transition. The broken symmetry appears as
a periodic density modulation in |¦ |
2
and the stan-
dard symmetry considerations for a melting transi-
tion apply [306]: the cubic term in |¦ |
2
enters the
usual Landau expansion for a liquid–solid transition
and a sharp first-order transition is expected where
translational (not U (1)) symmetry is broken (note
that no long range phase order is expected in the un-
pinned vortexlattice state [71,72,307]).This scenario
is confirmed by experiments through the observa-
tionofjumpsinthemagnetizationinBiSCCO[40]
and in YBCO [41] as well as the measurement of a la-
tent heat inYBCO [42,43] atthe vortex lattice melting
transition; the thermodynamic consistency between
the magnetic and calorimetric measurements has
been demonstrated via the Clapeyron relation [42].
AsimpleestimateforthejumpB in theinduction
is provided by the following scaling analysis ( [300]):
we start from the thermodynamic relation B =
−(4/V)@
H
G|
T
,withG the Legendre transform of
the free energy F,G(T, H)=F(T, B)−BHV/4,and
V the system volume.Attributingthe thermal energy
k
B
T
m
and the volume V
edf
to each elementary degree
of freedom we can estimate G ∼ k
B
T
m
V/V
edf
.The
volume V
edf
is determined by the dominant modes
leading to melting, which are located at the Brillouin
zone boundary with K
BZ
≈
√
4/a
0
.Hence,wecan
define the volume per degree of freedom in the form
V
edf
≈ a
2
0
L.Making use of the power-law dependence
of T
m
/V
edf
on H we obtain the jump
B =−
4
V
@G
@H
T
m
≈
k
B
T
m
HV
edf
=
k
B
T
m
¥
0
L
;
(12.262)
the numerical ≈ 1 follows from comparison with
results from numerical simulations [240,300]. In an
anisotropic material the important fluctuations in-
volve the wavevector k
z
∼ 1/"a
0
along the field and
thus L ≈ "a
0
.Wethenarriveatthefinalresultfor
the jump in B as it applies to continuous anisotropic
superconductors,
B ≈
k
B
T
m
¥
◦
"a
0
≈ 6. 10
−4
¥
◦
2
(T
m
)
, (12.263)
approaching zero as T
m
→ T
c
.Notethatinanin-
compressible (uncharged, e → 0and →∞)sys-
tem, we correctly find B → 0.Rewriting (12.263) in
the form B[G] ≈ (1.5·10
−6
/")T
m
[K](B
m
[G])
1/2
and
choosing " =1/8 we arrive at a good agreement with
the magnetization data of Schilling et al. [42, 308]
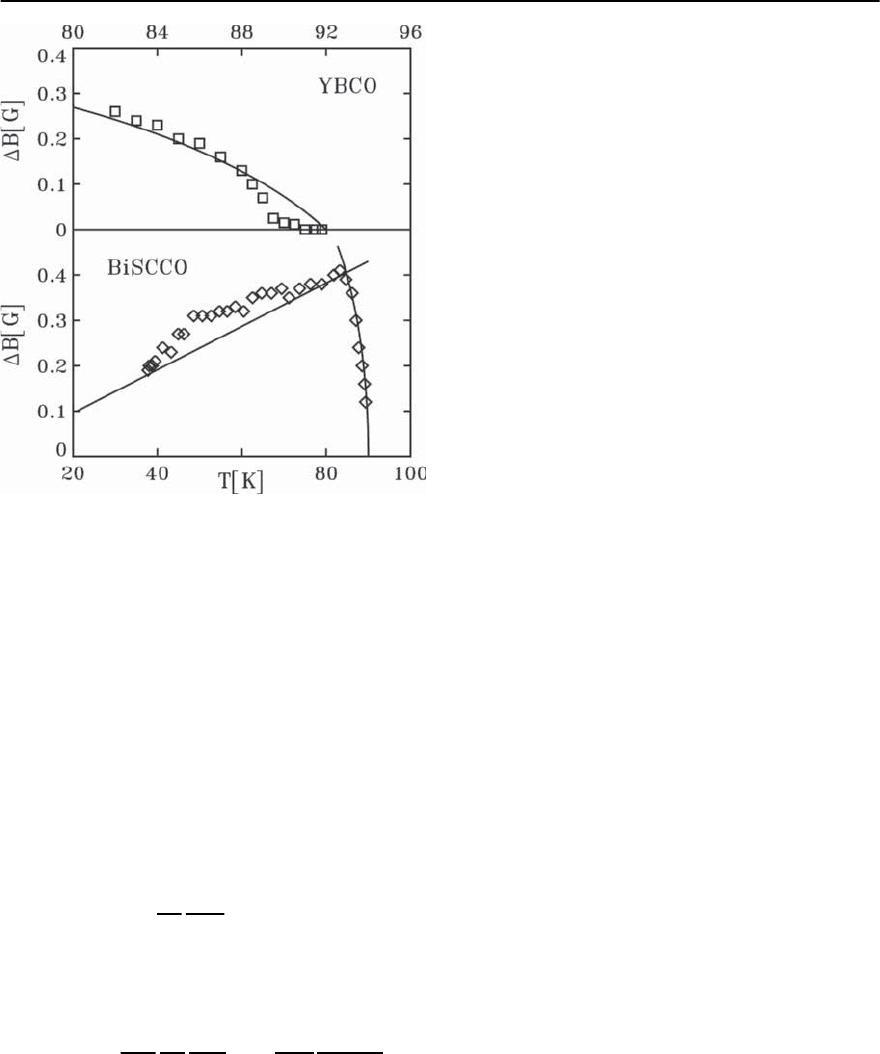
12 Vortex Matter 561
Fig. 12.18. Top :thejumpB in the induction versus temper-
ature T as measured in anYBCO single crystal [42] and cal-
culated from the expression (12.263). The deviations close
to the transition are possibly due to the increased rele-
vance of disorder. Bottom: the same for a BiSCCO single
crystal [40] using the result (12.266). The drop in B on
approaching T
c
is explained in terms of a temperature de-
pendent cutoff in the electromagnetic fluctuations through
the Josephson coupling at temperatures T > T
em
on an YBCO single crystal, see Fig. 12.18 (we have
made use of the experimentally measured melting
line B
m
(T)). The magnetization jump describes a
transition from a “dilute” vortex solid into a “dense”
vortex liquid, hence a vortex crystal melts like ice.
The jump s in the entropy density is easily de-
rived via the Clapeyron relation
s =−
1
4
dH
m
dT
B . (12.264)
This is converted into the entropy jump S
d
= a
2
0
ds
per vortex per layer (we approximate H
m
≈ B
m
away
from H
c
1
)
S
d
≈ −k
B
d
4L
T
m
B
m
dB
m
dT
≈ k
B
˛d
4L
T
m
T
c
− T
m
,
(12.265)
where we have assumed that the melting line van-
ishes B
m
∝ (T
c
− T)
˛
as T approaches T
c
in the last
equation.In the continuous anisotropic situation the
singular factor 1/(T
c
−T
m
)iscompensatedbythedi-
vergence of L ≈ "a
0
; on the melting line, the product
a
0
(1 − T
m
/T
c
) is (roughly) temperature independent
and we find a constant but material dependent en-
tropy jump per vortex per layer. Using parameters
for YBCO ((0) ≈ 1400 Å and d =12Å)weobtain
the value S
d
≈ 0.4 k
B
, in good agreement with ex-
periment [42]. Note that the entropy jump S
d
> 0
naturally describes a transition from the low-entropy
solid into a high-entropy liquid; combining the pos-
itive entropy jump S
d
> 0 with the retrograded
melting line dB
m
/dT < 0 the negative jump in the
magnetization appears as a direct consequence of the
Clausius–Clapeyron relation (12.264).
Note that the result (12.265) differs from the sim-
ple estimate S
d
∼ k
B
(d/L) by the important fac-
tor 1/(T
c
/T
m
− 1) which becomes large near T
c
;in
our derivation this factor stems from the shape of
the melting line which involves the dependence on
1−T/T
c
through the temperature dependence of
the Landau parameter ˛(T) (without this “internal”
temperature dependence the melting line would de-
crease according to B
m
∝ 1/T
2
). Deriving the en-
tropy jump directly from the free energy via the re-
lation S =−dF/dT care must be taken to take this
additional temperature dependence in the free en-
ergy into account, cf. [300].
In layered BiSCCO the melting line is pushed
down to low fields B
m
(T) < B
(T)overalargepor-
tion of the phase diagram. The dominant interaction
in the vortex system is given by the electromagnetic
one. The loosely bound pancake vortices undergo
large thermal fluctuations and dominate the melt-
ing process, hence L = d; the shape of the melt-
ing line is given by (12.212). Close to T
c
the Joseph-
son interaction becomes relevant as "(T) > d: for
T > T
em
≈ T
c
[1 − ("(0)/d)
2
]
1/2
the dominant fluc-
tuations at melting are cut off on the scale L ∼ "
and the melting line is given by (12.213).In a layered
material the jump B in the induction then takes the
particular temperature dependence

562 G. Blatter and V.B. Geshkenbein
B ≈
⎧
⎪
⎪
⎨
⎪
⎪
⎩
k
B
T
m
¥
0
d
, T
m
< T
em
,
k
B
T
m
¥
0
"(0)
1−T
2
m
/T
2
c
, T
em
< T
m
,
(12.266)
wherewehaveassumedthat ≈ 1. Note that it is
the temperature dependence of L, which goes from
"a
0
(T
m
) in a continuous anisotropic superconduc-
tor to L ≈ d and L ≈ "(T
m
)inalayeredmate-
rial, that leads to the different dependencies in the
jump B(T). The result (12.266) is in good agree-
ment with the experimental observations of Zeldov
et al. [40] (see Fig. 12.18; for BiSCCO we use param-
eters d =15Å,(0) = 2000 Å, " =1/400): At low
temperatures T
m
< T
c
−7KthejumpB increases
linearly with temperature.About 7 K before reaching
the transition, B drops sharply and vanishes at T
c
,
a behavior which can be explained in terms of the
crossover at T
em
, where the Josephson coupling be-
tween the layers becomes relevant and cuts off the
further growth of fluctuations.
The jump in the entropy again follows from the
general expression (12.265). In a layered material we
have to insert the length L ≈ d or L ≈ " and the sin-
gular factor T
m
/(T
c
− T
m
) remains uncompensated;
as a result, the entropy jump per vortex per layer di-
verges on approaching T
c
,
S
d
≈
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
k
B
1−(T
m
/T
c
)
2
, T
m
< T
em
,
3
4
d
"(0)
k
B
1−(T
m
/T
c
)
2
, T
em
< T
m
.
(12.267)
This divergence in the entropy jump upon approach-
ing T
c
is in agreement with experimental observa-
tions [40] and with the result of our melting analysis
in Sect. 12.7.5 above, cf. Fig. 12.15. Note that in this
latter case the divergence arises from 2D-like fluctu-
ations pushing the melting line to zero at T
BKT
;as-
suming a melting line in the form B ∝ (1 − 2T/"
0
d)
we obtain a divergent entropy
S
pc
≈ k
B
4
2T
"
0
d
1
1−2T/"
0
d
. (12.268)
12.7.7 Vortex Liquid
While the structure of a liquid (plasma,gas) of parti-
cles is intuitively understood, the structure of a line
liquid is less obvious. In particular, one could think
about a liquid state where the vortex lines still re-
main ordered with respect to their neighbors, see
the disentangled liquid in Fig. 12.19,or alternatively,
convey an entangled liquid where the vortex lines
wind around each other, effectively producing large
vortex loops, see Fig. 12.19. A very fruitful concept
allowing to quantify this idea has been put forward
by Nelson [11,305] who proposed a mapping of the
3D system of classical vortex lines to a system of 2D
quantumbosons:Consider thesimplifiedfree energy
F
T
=
1
T
L
0
dz
"
l
2
dR
dz
2
(12.269)
+
1
2
=
2"
0
K
0
|R
− R
|/
,
where the 2D coordinates R
(z)definethe(z-
dependent) positions of the individual lines. Here,
the first term describes the elastic energies of the
individual lines (of length L) while the second term
describes the interaction with K
0
()theMacDonald
function,K
0
( < 1) ∼ −ln; K
0
( > 1) ∼ e
−
/
√
.
Here,we approximate the non-local (in z)interaction
between vortex segments, see (12.62), by a local one
—thisapproximationisvalidaslongastheangular
distortions @
z
R
remain small, i.e., not to deep into
the vortex liquid phase.
The expression (12.270) should be compared with
the imaginary time () action of massive (m), two-
dimensional, interacting (q
2
)Yukawabosons,
S
B
=
1
B
B
T
B
0
d
m
2
dR
d
2
(12.270)
+
1
2
=
q
2
K
0
|R
− R
|/
,
with
B
and T
B
the parameters describing quan-
tum and thermal fluctuations. The bosonic statistics

12 Vortex Matter 563
Fig. 12.19. Possible equilibrium phases for
the vortex-liquid: disentangled vortex-liquid
(equivalent to the normal ground state of
2D quantum bosons) and entangled vortex-
liquid (superfluid groundstate of 2D quantum
bosons). The entangled liquid is characterized
by vortex-loop excitations (cooperative ring-
exchange processes) and is thermodynamically
equivalent to the normal metal phase
is realized through periodic boundary conditions
R
( =0)=R
P ( )
( =
B
/T
B
)withP apermutation
of the particles. The classical statistical mechanics of
the vortex system then can be mapped to the quan-
tum statistical mechanics of 2D bosons through the
identification T ↔
B
, z ↔ , L ↔
B
/T
B
, "
l
↔ m,
2"
0
↔ q
2
.
Rewriting (12.270) and (12.271) in dimensionless
form (we measure energies in units of q
2
, times in
units of
B
/q
2
, and lengths in units of a
, a
2
=
2/n
√
3 with the density n =1/a
2
0
),
S
B
=
ˇ
0
d
1
2
2
dB
dR
d
2
+
1
2
=
K
0
|R
− R
|/
, (12.271)
we identify two relevant parameters, the inverse tem-
perature ˇ and the de Boer parameter
dB
,
ˇ =
q
2
T
B
=
2"
0
L
T
,
dB
=
B
a
g
√
m
=
T
a
√
2"
l
"
0
. (12.272)
This mapping then brings together the physics of 3D
vortices with that of 2D quantum bosons, of which a
number of results are known.
The phase diagram for the Bose model, as shown
schematically in Fig. 12.20, contains three phases: A
high temperature normal liquid, a low temperature
(Wigner) crystal, and a superfluid due to large quan-
tum fluctuations. This can be understood heuristi-
cally by considering the three energy scales involved:
The transition from a normal liquid to a lattice is
determined by the competition between the ther-
mal energy 1/ˇ and the potential energy 1. In the
limit →∞and
dB
= 0 the (classical) tran-
sition takes place at ˇ
m
≈ 140 [269], cf. the dis-
cussion on the one-component Coulomb plasma in
Sect. 12.7.2. Increasing quantum effects, a further
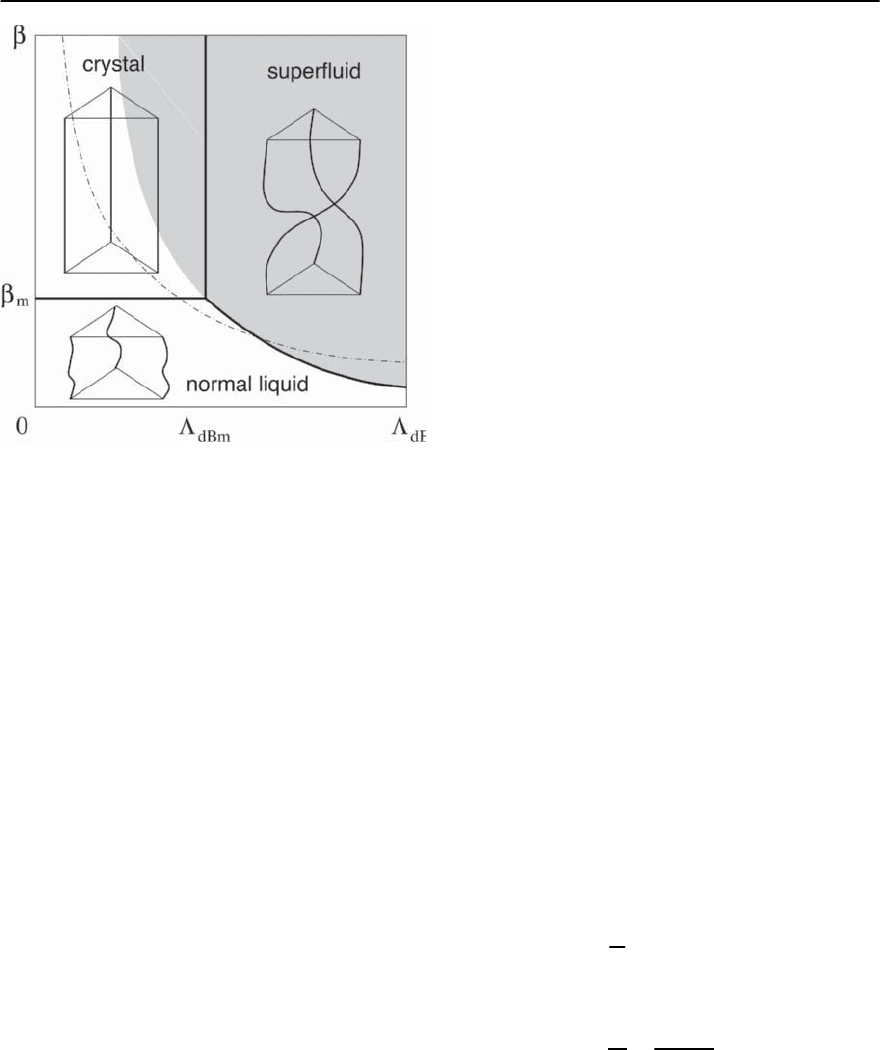
564 G. Blatter and V.B. Geshkenbein
Fig. 12.20. Schematic phase diagram for a system of 2D
charged bosons in terms of the de Boer parameter
dB
and
inverse temperature ˇ.Thesolid lines represent phase tran-
sitions; quantum fluctuations are relevant in the shaded re-
gion.In the vortex system the parameter
2
dB
= T
2
/2"
l
"
0
a
2
and ˇ =2"
0
L
z
/T. The constant field line for a thin sam-
ple (L
z
< 70T/"
0
)isshown(dashed-dotted line)asitruns
through all three phases. For thicker samples the line is
pushed upward
transition takes the normal liquid to a superfluid
when the thermal energy matches the kinetic energy,
2
dB
ˇ ≈ 1. Finally, at low temperatures, the compe-
tition between potential and kinetic energy deter-
mines whether the system is a crystal (
dB
<
dBm
)
or a superfluid (
dB
>
dBm
). For ˇ, = ∞,itis
known that
dBm
=0.062 [309].
The boson phase diagram can be reinterpreted
in terms of the vortex system, where ˇ is propor-
tional to the sample thickness and
dB
measures the
strength of thermal fluctuations. For thin samples,
ˇ < ˇ
m
, 1/
2
dB
,we find a disentangled vortex-liquid.
In thicker samples, the system is either a lattice or an
entangled vortex-liquid depending on temperature
and magnetic field. Note the non-trivial mapping
between the H–T and
dB
–ˇ phase diagrams: In a
thin sample, the constant field line (dashed-dotted
in Fig. 12.20) passes through the crystalline phase
(low T), the disentangled liquid phase (intermediate
T), and the entangled liquid phase (high-T). With
increasing L
z
, this line moves to higher values of ˇ,
the vortex lattice melting line is determined solely by
the value of
dBm
, and we recover the bulk melting
line in the form T
m
≈ 0.09 ""
0
a
(when compared
to (12.215) this corresponds to a Lindemann number
c
L
≈ 0.17; we use "
l
= "
2
"
0
for an anisotropic super-
conductor, while the 3D-XY simulations producing
the result (12.192) involve a slightly different effec-
tive elasticity [242]). Rigorously, the bosonic phase
transition into the superfluid state maps to a corre-
sponding phase transition in the vortex systemwith a
toroidal geometry.In a real vortex system the bound-
aries at z =0andz = L are free and the transition
transforms into a crossover, except for the thermo-
dynamic limit L →∞.
The phase diagram proposed in Fig. 12.20 is the
simplest possible one, but more complicated ver-
sions are possible in principle. In fact, the transi-
tion from the Wigner crystal to the superfluid in-
volves the change of two symmetries: the transverse
translational symmetry of the lattice and the gauge
symmetry of the superfluid. If these two symmetries
do not change simultaneously an intermediate phase
will appear,either a supersolid with both symmetries
broken [74] or a normal liquidwith none of the sym-
metries broken. The latter phase would correspond
to a disentangled vortex liquid (cf. Fig. 12.19) and
various arguments have been put forward in support
of such an intermediate phase [287,310]. However,
numerical simulations of the 2D quantum bosons
via a path-integral Monte Carlo technique [240] (see
also [311]) show that no such complication of the
phase diagram is realized, at least in the local ap-
proximation (12.271). To this end, the two symme-
tries in the problem are traced via a measurement of
the structure factor
S(K, )=
1
N
9
K
()
−K
(0)
:
(12.273)
and of the winding number [312]
n
s
n
=
W
2
2
2
ˇN
. (12.274)
Here,
K
() is the partial Fourier transform of the
density operator, (R, )=
ı[R − R
()] and
12 Vortex Matter 565
W =
ˇ
0
d@
R
is the winding vector measur-
ing the diffusion of the center-of-mass of the sys-
tem in imaginary time (periodic boundary condi-
tions R
(0) = R
P ( )
(ˇ)areused,withP apermuta-
tion of the N bosons; n
s
, n denote the superfluid and
total density, respectively, and N is the number of
bosons, N = 36–64 in the simulations of [240]; for
larger systems,the fraction of entangled lines n
e
/n is
measured instead of n
s
/n).
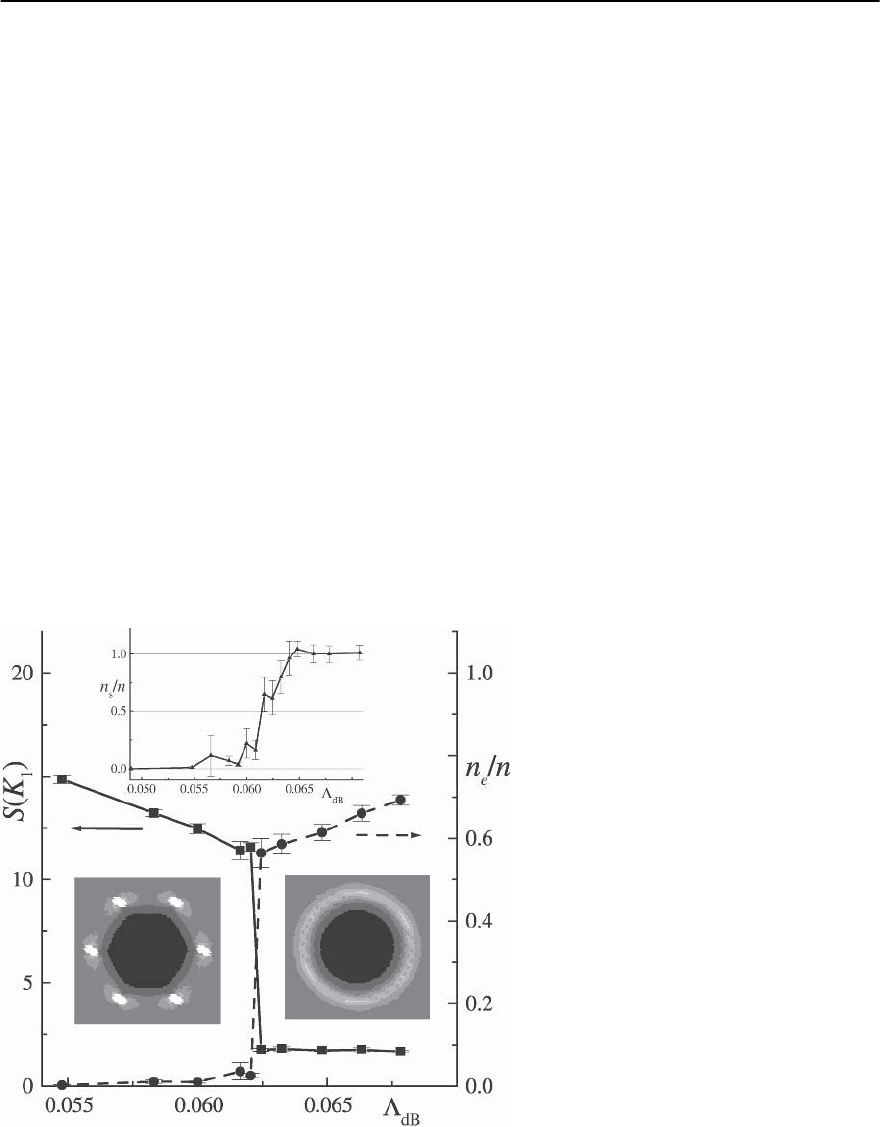
Figure 12.21 shows the first Bragg peak S(K
1
)and
the superfluid/entanglement fractions n
s
/n and n
e
/n
as a function of the de Boer parameter
dB
;asthe
Bragg peak collapses at
dBm
=0.062 the superfluid
density rises steeply, showing that the system under-
goes a sharp (first-order) transition from a crystal
to a superfluid (entangled) liquid. As an additional
result these simulations provide quantitative results
for the jumps in the energy and in the density at
the transition which compare well with the jumps in
entropy and magnetization observed in experiments
on YBCO single crystals [240], cf. Sect. 12.7.6 above.
12.7.8 Constitut ive Relation
Thermal fluctuations of the vortex lines also change
the constitutiveB(H) relation and modify the mean-
field results (12.56) and (12.57) for the magnetiza-
tion [151,313,314],particularly in 2D thin films and
in layered superconductors. Their effect is most dra-
matic near the onset of the vortex phase where fluctu-
ations change the functional behavior (12.55) at the
H
c
1
transition and even render the transitionfirstor-
der at low temperatures. While these effects are very
interesting from a theoretical point of view, their ex-
perimental observation appears to be difficult.
In determining the new constitutiverelation B(H)
we have to include additional terms in the free en-
ergy density f which arise from thermal fluctuations
of the vortex lines. One obvious term is the entropy
contribution −Ts
l
of a fluctuating line [11]. The line
entropy of an isolated line s
l0
(T) is reduced by the
potential cage set up by the surrounding vortices,
s
l
(T, a
0
)=s
l0
(T)−(1/L)ln˛
L/L
T
with the thermal
collision length L
T
≈ "
l
a
2
0
/T and the numerical con-
stant ˛ > 1. The free energy density
Fig. 12.21. The first Bragg peak and the entan-
glement parameter n
e
/n for a system with 64
lines and ˇ = 300. A sharp transition from
a crystal to an entangled liquid is found at
dBm
=0.062. The structure factors just before
and after the melting transition are displayed.
The inset shows the superfluid density n
s
/n for
a system with 36 lines

566 G. Blatter and V.B. Geshkenbein
g(B)=
B
¥
0
l
1−
Ts
l0
l
−
H
H
c
1
(12.275)
+6K
0
(
¥
0
/B)) +
T
2
"
l
a
2
0
ln ˛
then picks up an additional steric repulsion ∝ T
2
/a
2
0
due to the above entropy reduction (here,
l
denotes
the line energy). Minimizing g(B)withrespecttoB
we obtain the new constitutive relation B(H): Close
to the transition the vortex density 1/a
2
0
= B/¥
0
is small and the steric repulsion dominates over
the usual repulsive interaction due to the vortex
currents; as a result we obtain the new constitu-
tive relation B ∼ ("
l
l
2
/T
2
)[H − H
r
c
1
], changing
the logarithmic mean-field result (12.55) into an
algebraic form. In addition, the field-independent
line entropy s
l0
renormalizes the lower critical field
H
r
c
1
= H
c
1
(1 − Ts
l0
/
l
). Note that the long-wavelength
elasticity "
l
relevant at low fields is equal to the line
energy, "
l
≈
l
∼ "
0
. A similar renormalization of
H
c
1
due to disorder is discussed in [315,316].
Inlayeredsuperconductorsadditional shortwave-
length distortions of the vortex lines have to be ac-
countedfor.Theseshort wave-length distortions pro-
duce an attractive vortex–vortex interaction of the
van der Waals type: Consider the case of a magnet-
ically coupled layered system with two straight vor-
tices 1 and 2 at a distance R.Displacing an individual
pancake vortex in stack 1 by u
1
is equivalent to plac-
ing a pancake-vortex–anti-pancake-vortex pair, i.e.,
a pancake-vortex dipole d
1
,ontothevortexline.The
pancake-vortex dipole d
1
induces a second dipole
d
2
in vortex 2 within the same layer. With two pan-
cake vortices interacting logarithmically within the
same layer, the force from dipole d
1
acting on vortex
2 follows a 1/R
2
law, hence d
2
∼ d
1
2
/R
2
. Finally,
the interaction potential between two vortex dipoles
follows a 1/R
2
behavior as well and we obtain a long-
range attractive potential V
vdW
∼ (d
1
/)
2
4
/R
4
be-
tween the vortex segments.Forthermally driven fluc-
tuations we have d
2
1
∝ u
2
1
and the van der Waals at-
traction takes the form V
vdW
∼ (T/d)(/R)
4
[317]
(alternatively, the fluctuations can be driven by dis-
order [318] or, at low temperatures, quantum me-
chanically). This additional attractive vortex–vortex
interaction adds a contribution −(T
4
/d)(B/¥
0
)
3
to
the Gibbs free energy density g whichdrivesthetran-
sitionfirst-orderatlow temperatures [317].With a fi-
nite Josephson coupling " > 0 the attraction decays
∝ (/R)
5
, V
vdW
∼ (T/")(/R)
5
(the power-laws
R
−4
and R
−5
correspond to the well known ∝ r
−6
and
∝ r
−7
behavior of the usual van der Waals attrac-
tion between neutral atoms). The relation between
the van der Waals attraction of vortex lines and the
Casimir effect in vortex systems is discussed in [319].
12.8 Quenched Disorder: Pinning and Creep
Defects produce an inhomogeneous material and pin
the vortices at energetically favorable locations in the
crystal. The transport and magnetic properties of a
bulk superconductor then are described by the Bean
model [320]: vortex pinning leads to the formation
of a vortex density gradient which is equivalent to
a current flow j in the bulk via Maxwell’s equation
j =(c/4)∇∧B with B = n
v
¥
0
ˆz, n
v
the vortex
density. This current flows free of dissipation and
hence the optimization of the defect structure in a
material is an important goal regarding applications.
Science-wise, the problem of pinning confronts us
with the physics of instabilities (strong pinning) or
with the statistical summation of competing forces,
a challenging problem in classical statistical physics
(collective pinning).
The maximal vortex density gradient is obtained
when the pinning force density F
pin
acting on a vor-
tex becomes equal to the driving Lorentz force den-
sity, resulting in a critical or depinning current den-
sity j
c
,
1
c
j
c
∧ B = F
pin
. (12.276)
Usually, this critical current density is consider-
ably reduced with respect to the depairing current
density j
0
, which can be estimated from Maxwell’s
equation ∇∧B =(4/c)j to be of the order of
j
0
≈ cH
c
/4 ∼ c"
0
/¥
0
, see (12.7) for the exact
result from GL theory.
The critical current density depends strongly on
the strength of the pinning force. Since the Lorentz
force is a force per unit volume, pinning has to pro-
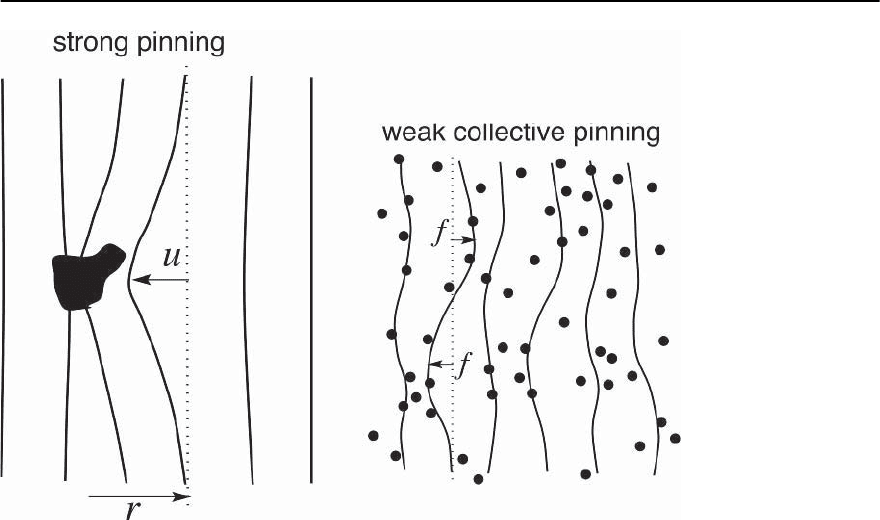
12 Vortex Matter 567
Fig. 12.22. Left:Strong
pinning centers due to
individual defects pro-
duce large displace-
ments (plastic defor-
mations) in the vortex
lattice. The vector r de-
notes the position of
the unperturbed lattice
far away relative to the
impurity; the displace-
ment u points in the op-
posite direction.
Right: Weak pinning
duetopoint-likedisor-
der. The forces f orig-
inating from different
impurities compete due
to the elastic proper-
ties of the vortex lattice,
hence forces add ran-
domly within the col-
lective pinning volume
duce a force per unit volume, too. In the strong pin-
ning situation [6, 10, 134] defects act individually
and produce plastic deformations (see, Fig. 12.22)
[171,321,322]);the pinning forcethen is given by the
product of the active defect density and the average
pinning force, see Sect. 12.8.1 below. In the copper-
oxides a strong pinning situation naturally appears
due to the layered structure, resulting in individual
pancake-vortex pinning at low magnetic fields, cf.
Sect. 12.9.7 [64,323,324]. When pinning is weak, the
elastic forces dominate over the pinning forces and
the defects compete, see Fig. 12.22; we then are faced
with the problem of the statistical summation of in-
dividualpinning forces.Weak point-like pinningcen-
ters pose a generic problem relevant in a number of
physical situations and the corresponding summa-
tion problem has been solved by Larkin and Ovchin-
nikov within their weak collective pinning theory,see
Sects. 12.8.2 and 12.9 [8,10] (similar concepts have
been applied to the problem of charge density wave
pinning [325–327]). Such point-like pins produce an
uncorrelated disorder landscape; other types of de-
fects, such as columnar tracks produced by heavy
ion irradiation [29,30, 55, 89–91] or twin bound-
aries [27, 28, 328, 329] generically present in some
of the copper-oxides, produce a correlated pinning
potential and will be discussed in Sect. 12.10.
A third distinction in the type of pinning, be-
sides “strong” versus “weak” and “correlated” versus
“uncorrelated”, is between “bulk” and “non-bulk”.
The classic example of a “non-bulk” type pinning
is that due to surface barriers [330]; furthermore,
the platelet shape of layered copper-oxide supercon-
ductors (e.g., BiSCCO) produces the even stronger
geometrical barriers [331–333], see Sect. 12.11.
12.8.1 Strong Pinning
The classic arguments characterizing strong pinning
go back to Labusch [6], see also [10, 134]: In order
to calculate the mean pinning force acting on the
vortex lattice one has to determine the interaction
of the latter with an individual strong pinning center
and then average the forceover randomly positioned
impurities or defects. At low impurity concentration
n
imp
, the displacement fields of different defects do
not interfere and the critical current density j
c
can
be obtained within a linear approximation in n
imp
,
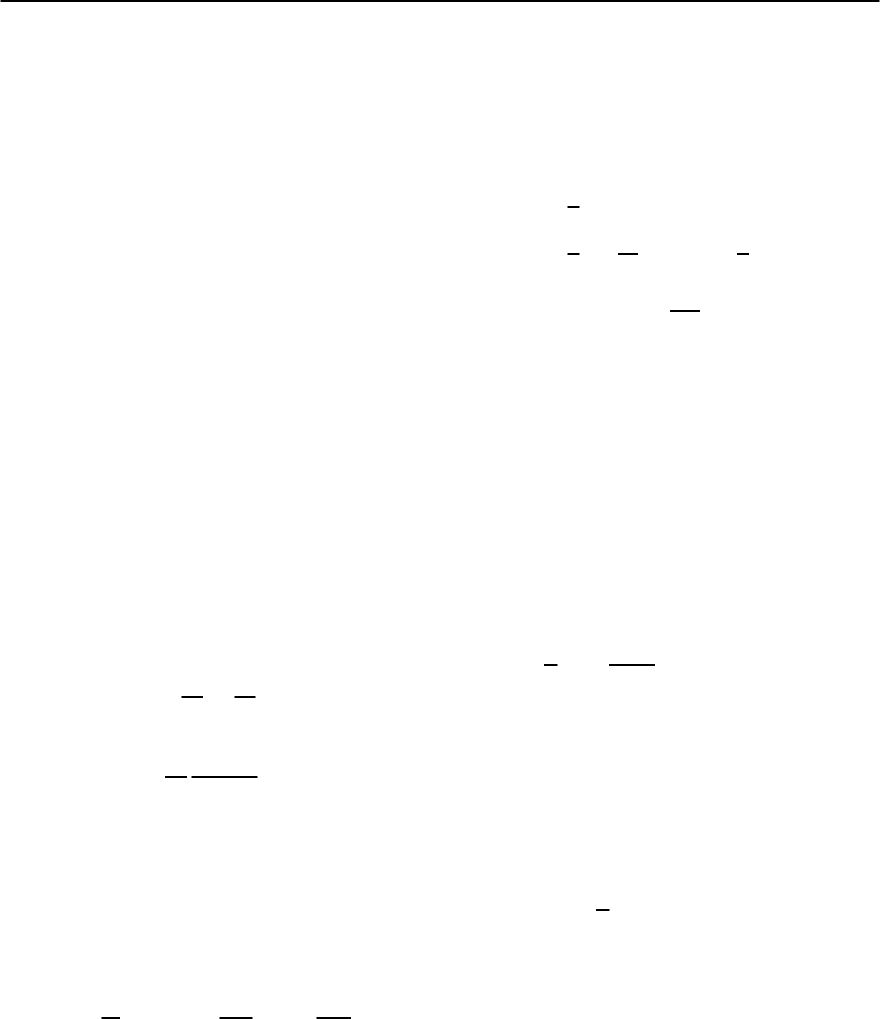
568 G. Blatter and V.B. Geshkenbein
j
c
∧ B/c = F
pin
= n
imp
f
pin
. (12.277)
The pinning force of an individual impurity f
pin
de-
rives from the free energy e
pin
(r) of the vortex system
in the presence of the impurity,
f
pin
=−∇
r
e
pin
(r) , (12.278)
where r denotes the position of the unperturbed lat-
tice relative to the impurity, see Fig. 12.22. If pinning
is weak the energy landscape e
pin
(r) is a single val-
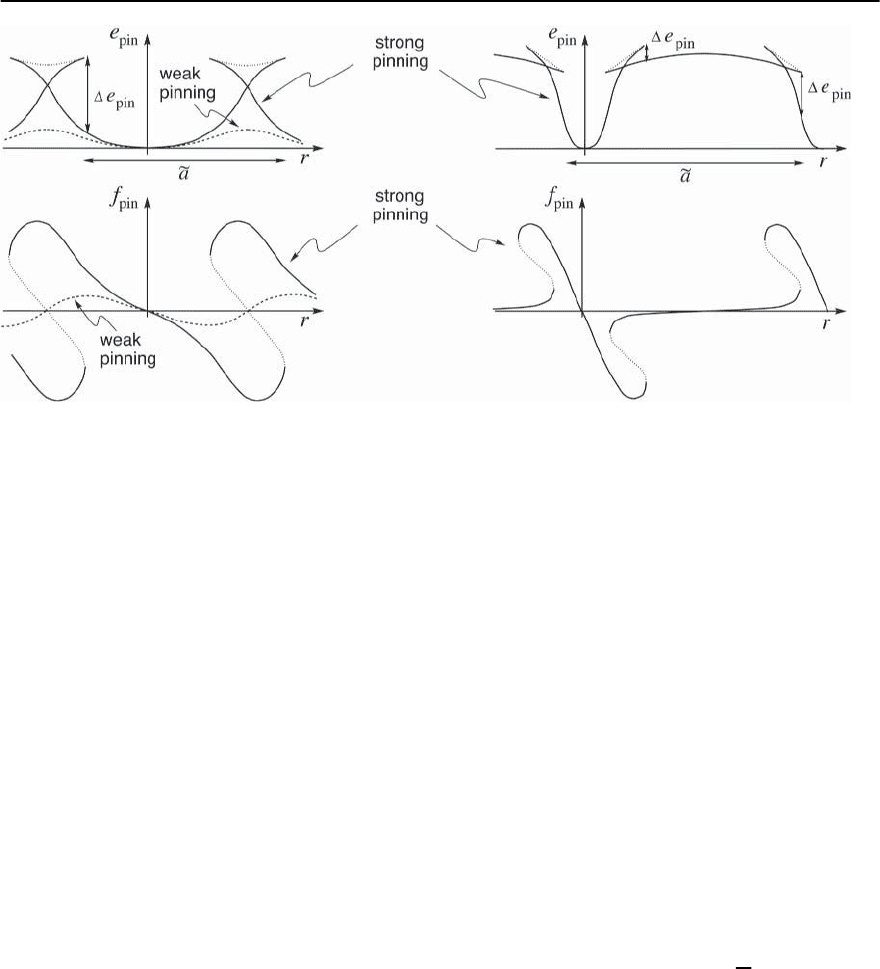
ued periodic function (see Fig. 12.23, usually with a
period ˜a of the order of the lattice spacing a
0
)and
averaging the pinning force over impurity positions
the resulting force is zero — weak pinning is due to
fluctuations in the defect structure and thus collec-
tive, see Sects. 12.8.2 and 12.9 below.
Strong pins induce plastic deformations in the
vortex lattice and the energy landscape e
pin
(r)be-
comes a multi-valued function in the displacement
r [6], see Fig. 12.23; as a result the averaging process
produces a non-zero pinning force determined by the
jump e
pin
connecting different metastable states:
Choosing r along the x-direction,we first express the
average along the x-axis over the force −@
x
e
pin
(x, y)
through the jump e
pin
(y) in the pinning energy,
f
pin
=−
L
x
0
dx
L
x
L
y
0
dy
L
y
@
x
e
pin
(x, y)
=
a
0
0
dy
a
0
e
pin
(y)
˜a(y)
. (12.279)
The jump e
pin
(y) depends on the “impact param-
eter” y, the asymptotic transverse distance between
the pin and the trapped vortex line.Assuming a max-
imal transverse trapping distance t
⊥
along the y-axis
and approximating ˜a ≈ a
0
we obtain the mean pin-
ning force
f
pin
≈
t
⊥
a
2
0
e
pin
(0) ≈
t
⊥
t
a
2
0
f
imp
≈
S
trap
a
2
0
f
imp
,
(12.280)
wherewehaveexpressedthejumpe
pin
(0) ≈ t
f
imp
in terms of the typical impurity force f
imp
acting
over the bistabilityrange t
of the functione
pin
(x, 0);
the product t
⊥
t
then defines the trapping area S
trap
associated with the strong pin. Note that this trap-
ping area approaches zero at the crossover to weak
pinning where the bistable region vanishes. The in-
dependent action of these strong pins finally deter-
mines the critical current density
j
c
=
c
B
n
imp
f
imp
≈
c
B
n
imp
t
⊥
a
2
0
e
pin
(0) ≈
c
B
n
eff
f
imp
∼ j
0
n
imp
S
trap
f
imp
"
0
, (12.281)
with the effective impurity density n
eff
=
n
imp
(S
trap
/a
2
0
) and the depairing critical current j
0
∼
c"
0
/¥
0
.
In order to derive a quantitative criterion for
strong pinning we consider a single defect center at
r
pin
. Such a point-like defect exerting a force f
pin
(r)
on the vortex produces a deformation at the impurity
u
˛
(r
pin
)=
d
3
rG
˛ˇ
(r
pin
, r)f
pin,ˇ
(r)=
¯
C
−1
f
˛
,
(12.282)
with (cf. (12.92))
1
¯
C
=
d
3
k
(2)
3
G
˛˛
(k) . (12.283)
In (12.282) we have assumed an impurity with a
force profile of width smaller than the lattice con-
stant a
0
. As the vortex lattice deforms (by u)inre-
sponse to the force exerted by the defect we should
evaluate the force in (12.282) at the position r + u
and the displacement u(r) has to be determined self-
consistently from
u(r)=
1
¯
C
f
pin
[r + u(r)] . (12.284)
For weak pinning the displacement u is small and
the solution u(r) ≈ f
pin
(r)/
¯
C is a single-valued func-
tion.Strong pinning,however,produces multi-valued
functions u(r)andf
pin
(r), cf. Fig. 12.23. The solu-
tion of (12.284) turns multi-valued whenever the
displacement collapses, i.e., when @
x
u →∞(we
move the vortex lattice in the x-direction). Deriv-
ing (12.284) with respect to x we find that u
=
12 Vortex Matter 569
Fig. 12.23. Energy landscape e
pin
and pinning force f
pin
versus displacement r of the vortex lattice relative to the defect.
In the weak pinning case the energy landscape e
pin
is a single-valued function in r (dashed lines), while strong pinning
produces plastic deformations and renders e
pin
multi-valued (solid lines; dotted lines indicate unstable branches). The
average pinning forcef
pin
is determined by the jump e
pin
connecting different metastable branches. Left:largedefects.
Right:smalldefectswithr
pin
< a
0
f
pin
(x + u)/[
¯
C − f
pin
(x + u)] (note that x > 0im-
plies u < 0)andwearriveatthe(Labusch)criterion
@
x
f
pin
=−@
2
x
e
pin
=
¯
C ; (12.285)
hence, in order to produce strong pinning the (neg-
ative) curvature of the pinning energy e
pin
has to
overcompensate the elasticity of the lattice (note that
the curvature in the potential minima is positive; the
Labuschcriterion involvesthe maximal negative cur-
vature above the inflection point). A strong pinning
situation then occurs whenever the curvature in the
pinning energy becomes large or the elastic moduli
take on small values. Note that the Labusch criterion
tests an individual isolated pinning center and clas-
sifies it as a weak or strong one.
12.8.2 Weak Collective Pinning
When the displacement fields u produced by individ-
ual impurities remain single valued the pinning cen-
ters are weak; trivial averaging over these individual
pinning forces results in a zero average pinning force
density, cf. (12.280). In this situation, pinning is due
only to local fluctuations in the pinning force den-
sity. The competition between elastic and pinning
forces then produces a sublinear growth of the pin-
ning energy E
2
pin
(V)
1/2
with volume V ∼ L
d
:Letus
characterize the disorder potential by the density of
pins n
imp
of size r
pin
∼ and the individual pinning
force f
imp
. Due to the competition between the pins,
the individual pinning forces add up only randomly
within the volume V ∼ L
d
and the fluctuations in
the pinning energy E
2
pin
(V)
1/2
canbewrittenas
E
2
pin
(V)
1/2
≈
f
2
imp
n
imp
(/a
0
)
2
V
1/2
r
pin
,
(12.286)
where the factor (/a
0
)
2
accounts for the fact that
only the vortex cores are pinned by the disorder. The
result (12.286) implies that the pinning force acting
on an individual stiff vortex grows only sublinearly
in the volume V , E
2
pin
(V)
1/2
∝
√
V. Since the driv-
ing Lorentz force increases linearly with volume we
have to conclude that a stiff vortex lattice is never
pinned and hence the critical current density van-
ishes in this limit. On the other hand, a real vortex
lattice is characterized by a finite elasticity allowing
its accommodation to the pinning potential on some
