Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

530 G. Blatter and V.B. Geshkenbein

ıF[ı'] ≈





2



1+g



∇

(2)

ı'



16(1 + g)

(ı'

)



1−cos¥

n+1,n





8



r (∇∧ıA )

. (12.154)

Comparing with (12.97) we note the factor g/(1 + g)

which accounts for the suppression of the superﬂuid

density due to the presence of the pancake vortices.

This suppression is substantial for fields B  B

where g ∼ B

/B  1, while no renormalization ap-

pears at low fields B  B

where g  1 and hence

g/(1 + g) ≈ 1. Note that at low fields we can drop

the shear term ∝ (

ı'

)

in comparison with the

electromagnetic and Josephson tilt energies. On the

other hand, at high fields where the shear term dom-

inates g is small and we can drop the factor (1 + g)

−2

in the shear term.

Therenormalization of the (short wavelength) su-

perﬂuid stiffness due to the presence of pancake vor-

tices affects various properties of the vortex system

inlayeredsuperconductors:importantmodifications

appear in the context of the vortex (lattice) structure

associated with a finite in-plane field component B

see Sect.12.5.5,and in the analysis of the ﬂuctuation-

induced decoupling transition, see Sect. 12.7.3.

12.5.5 Vortex Lattice

In a continuous anisotropic superconductor the

tilted vortex lattice usually preserves its triangular

structureup to a trivialdistortion,see(12.78).Devia-

tionsoccur atlowfieldsH < H

wheretheattrac-

tive interaction between tilted vortices [179,182,183]

leads to the chain state [179–181]). Increasing the

anisotropy, an individual tilted vortex turns unsta-

ble [212] within some angular regime, suggesting

that in layered material the vortex lattice may split

into two separate families of pancake-vortex stacks

and Josephson vortices,each definingone of the field

components B

and B

, respectively [195, 213, 214].

Indeed, for weak Josephson coupling (we assume

 > ) the pancake vortices mainly interact elec-

tromagnetically and their homogeneous tilt costs a

large amount of magnetic energy; at the same time,

the field component B

parallel to the layers can pen-

etrate easily into the superconductor in the form of

Josephson vortices. In this situation a new struc-

ture with a lattice of Josephson vortices coexisting

with a lattice of pancake vortex stacks, the so-called

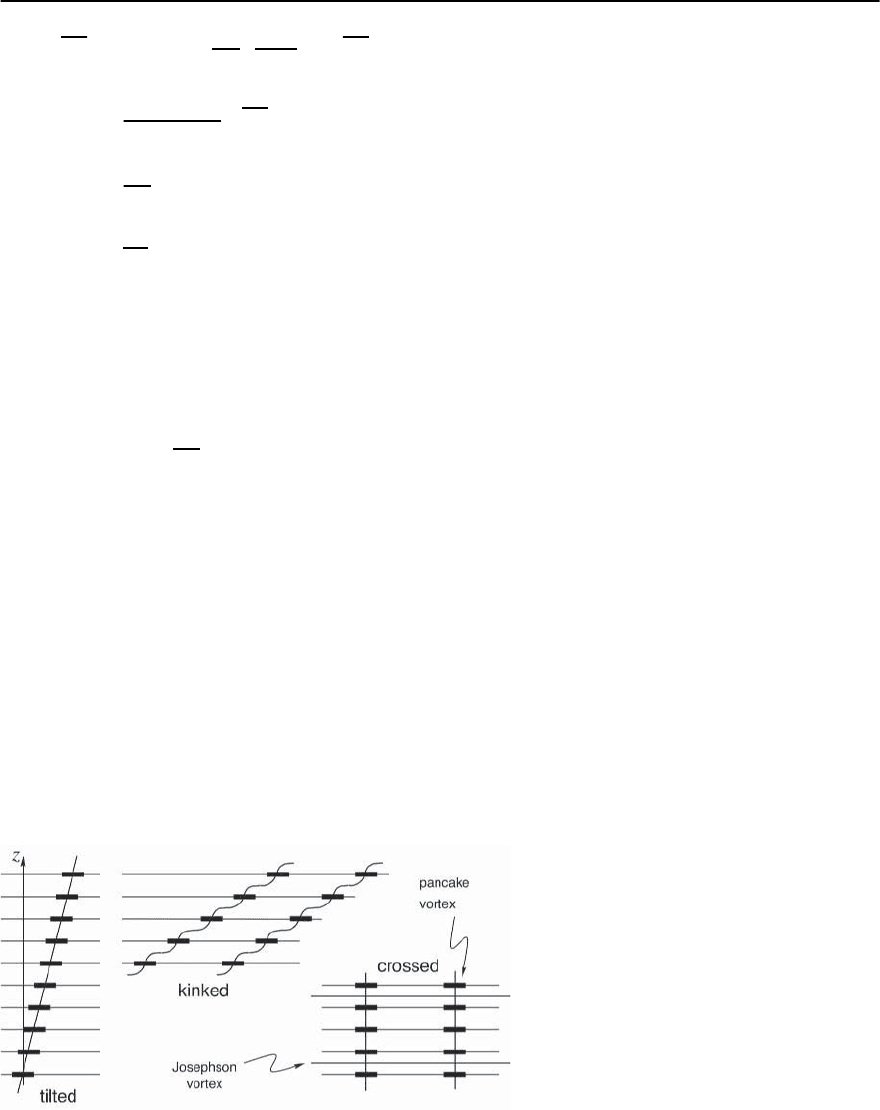
crossing lattice,may be energetically more favorable,

see Fig. 12.8. Comparing the energies of the tilted

vortex lattice and the crossing vortex lattices within

the Lawrence–Doniach description,Benkraouda and

Ledvij [214] indeed find the crossing-lattices state

to be stable within an intermediate angular regime

away from the extremal angles  =0, /2ifthemag-

netic field is low enough; on the other hand,the tilted

lattice remains stable in the vicinity of the high-

symmetry directions perpendicular and parallel to

Fig. 12.8. Schematic drawing of tilted and

crossed vortex lines/lattices where individual

vortex lines can be identified. In the crossed

vortex lattice Josephson vortices and pancake

vortices define two interpenetrating lattices

12 Vortex Matter 531

the superconducting planes. Below we compare the

energies of the two states and determine the transi-

tion angle 

separating the (nearly c-axis directed)

tilted vortex lattice ( < 

) from the crossed (or

combined) lattice (

< ). In doing so, we fol-

low [210] and account for the renormalization of the

superﬂuid density due to the pancake-vortex lattice

as derived in Sect. 12.5.4 above; the suppression of

the superﬂuid density then favors the crossed lattice

phase.

A direct consequence of the crossed-lattices vor-

tex state is the appearance of a (mixed) vortex-chain

state in layered superconductors, where either a frac-

tion or even all pancake-vortex stacks are pinned

onto stacks of Josephson vortices [210, 215]. This

unconventional vortex state has been observed in

Bitter decoration experiments on layered BiSCCO

superconductors [216]. Note that this vortex-chain

state is different from the chain state appearing in

anisotropic superconductors at small tilted fields, cf.

the discussion in Sect.12.4.1: whereas the chain state

in continuous anisotropic superconductors is a con-

sequence of the attractive interaction between tilted

vortices [179,182,183],the chain state in layered su-

perconductors is due to an attractive force appearing

between stacks of Josephson and pancake vortices.

Crossed Lattices

In order to find the transition angle 

near the c-

axis separating tilted and crossing vortex lattices we

compare their free energies [210]: Tilting the field by

the (small) angle  ≈ B

away from the c-axis we

have to pay for the tilt energy density

tilt

(k =0)



, (12.155)

with the homogeneous tilt modulus c

(0) = B

/4 +

3.7 ¥

/(4)

; while the first term derives from the

limit k → 0ofc

(cf. (12.83)), the second term

is the contribution from individual pancake-vortex

stacks in the limitk

→ 0,c

≈ ("

/2

) ln(1 +

/4) ≈ 2¥

/(4)

(see [217] for a precise

evaluation of the numerical prefactor).

On the other hand,leaving the pancake-vortex lat-

tice unchangedand adding a Josephson vortex lattice

in the ab-plane we have to account for the free en-

ergy density associated with the latter. However, the

Josephson vortices themselves are modified by the

presence of the pancake vortices through the renor-

malization of the superﬂuid stiffness,cf. Sect. 12.5.4:

For fields B

> B

the suppression of the in-plane

superﬂuid density by g leads to a reduction in the ef-

fective anisotropy," →˜" = "/

√

g.Asa consequence,

the Josephson length  describing the 2D core of a

pancake vortex and the phase core of the Josephson

vortex is reduced,  →

 =

√

g, as is easily seen

by comparing in-plane and out-of-plane energies in

(12.154). Similarly, the line energy of the Josephson

vortex is modified, 

→



√

g

; again, this fol-

lows trivially from (12.154) after isotropizing the ki-

netic energy terms along the x and z directions and

integration over the region [

, / ˜"]awayfromthe

phase core where the discrete structure is unimpor-

tant. Finally, the Josephson-vortex lattice structure

is modified too, taking a less anisotropic form with

short and long basis vectors ∼

√

˜"a

and ∼ a

√

˜".

Note that we ignore here an additional reduction

factor c(T)=cos(¥

n+1,n

)

in the Josephson cou-

pling due to thermal ﬂuctuationsof pancake vortices,

see [210].

Taking the above modifications into account, the

Josephson vortex lattice contributes with the energy

density, cf. (12.54),

8

2¥

√

g""



"¥

√



. (12.156)

Comparing the two energy densities the terms B

/8

cancel and the remaining corrections determine the

critical angle (we choose a cutoff u

∼ a

/ in g,

cf. (12.159) below)



≈ 24.1

"









1/2

. (12.157)

In the most interesting low-field part of the phase

diagram (with B of order B



= 

/

) the crossed

vortex lattice is favored as soon as the field is tilted

beyond the angle 

of order 1–10 degrees.

Chain State

The second interesting peculiarity of the low-field

vortex lattice in layered superconductors is the

532 G. Blatter and V.B. Geshkenbein

vortex-chain state, where a finite fraction of the

pancake-vortex stacks are pinned onto the stacks

of Josephson vortices [210,215,216]. Thisrearrange-

ment is a consequence of the attractive interaction

between a pancake-vortex stack and a Josephson vor-

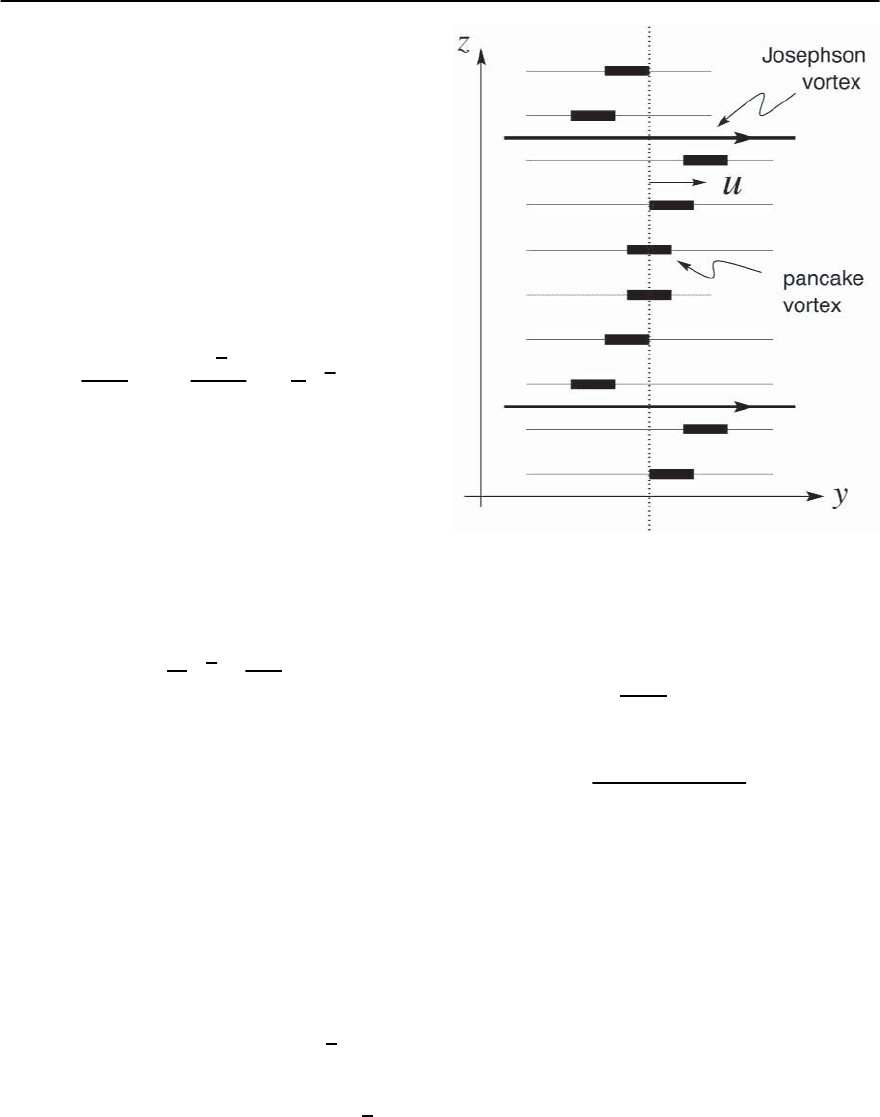
tex. Consider a pancake-vortex stack in the current

field set up by a Josephson vortex directed along the

y-axis, see Fig. 12.9: the Lorentz force acting on the

pancake vortices deforms the stack and allows the

system to gain energy. In order to estimate the dis-

placement u

of the pancake-vortex stack we start

from the screening current density j

set up by the

Josephson vortex,

∼

egn

' ∼

√

g¥



∼ j





√

g , (12.158)

where we have assumed large fields B > B

such that

g/(1 + g) ≈ g. This current drives the distortion of

the pancake-vortex stack, shifting pancake vortices

residing above and below the Josephson vortex core

in opposite directions along the axis of the Josephson

vortex,see Fig.12.9.The distortion is counteracted by

the electromagnetic force ("

d/

confining the

pancake-vortex stacks; comparing the two forces we

obtain the estimate

∼





√

g ∼

a



. (12.159)

In low fields B

< B

, g/(1 + g) ≈ 1 and the dis-

tortion u

∼ 

/ (note that u

also determines the

displacement u

entering the suppression factor g,cf.

(12.150)).

Returning to the chain state we consider a weak c-

axis field B

< ¥

/

= B



< B



, then each Joseph-

son vortex corecontainsonlyonerowofpancakevor-

tices (we assume non-overlapping cores, B

< B



/";

note that B

< B



implies g/(1 + g) ≈ 1). These

pancake vortices are pinned to the Josephson vortex

core with an energy ∼ ("

d/

∼ "

d

/

consequence of the distortion of the pancake-vortex

stack due to the current of the Josephson vortex (see

Fig. 12.9; with g/(1 + g) ≈ 1 the distortion is of

order u

∼ 

/). With a distance

√

" a

) between Josephson vortices along the c-axis,

a pancake-vortex stack pinned onto the Josephson-

vortex stack gains theline energy ∼ "

d

√

" a



Fig. 12.9. Deformation of a pancake-vortex stack in the cur-

rent field of Josephson vortices. The displacement u away

from the straight line configuration (dotted line)islarge,

of order u ∼ a

/

On the other hand, moving a pancake-vortex stack

from the bulk to the Josephson-vortex stack costs a

shear energy ∼ "



/ exp(−a

/); for fields B

below

chain

∼







/"

 (12.160)

the chain state is energetically favorable. Recent ex-

periments on BiSCCO single crystals have unraveled

acomplexB

-B

phase diagram with various vor-

tex lattice phases (tilted, crossed, chain-state, mixed

chain-lattice state) [218–221].

12.6 Anisotropic Scaling Theory

The discovery of high temperature superconductiv-

ity has enforced the rapid development of the phe-

nomenology of anisotropic type II superconductors.

Anisotropy has been traditionally incorporated into

12 Vortex Matter 533

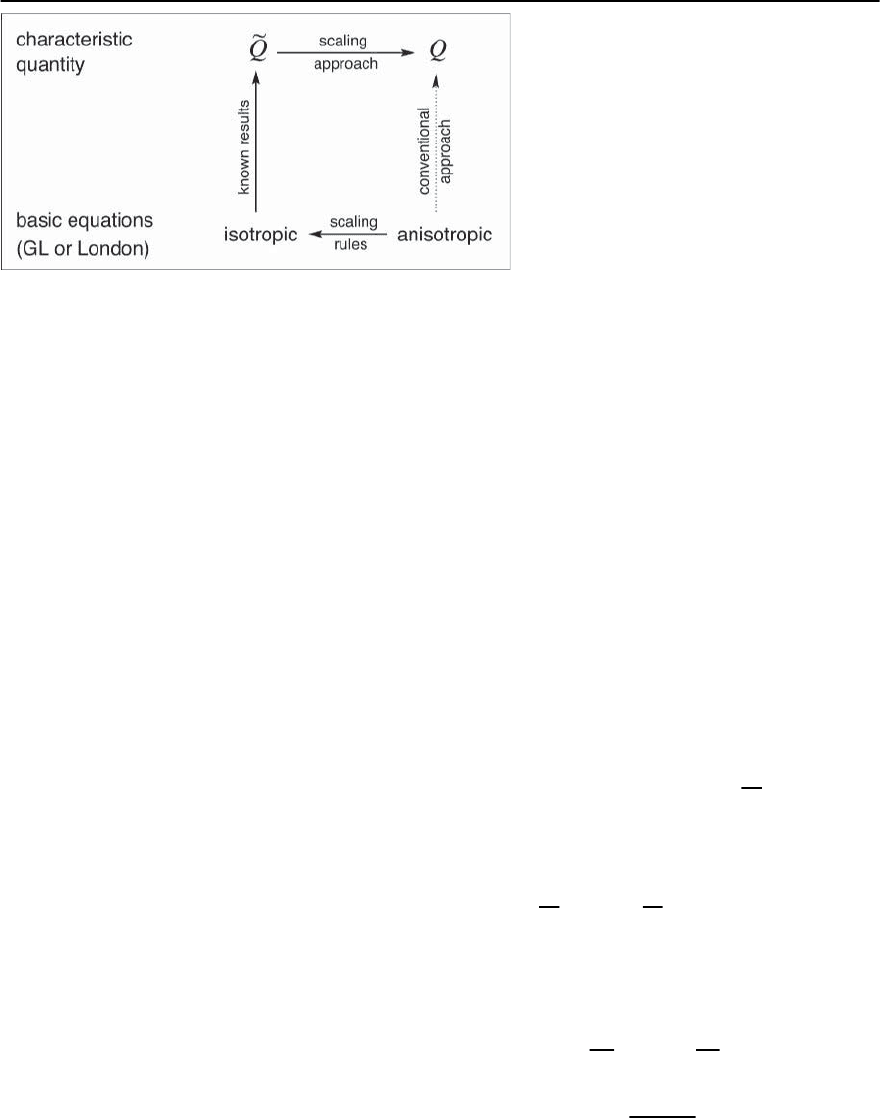
Fig. 12.10. Schematic comparison of the tradi-

tional and scaling approach for obtaining phys-

ical results in anisotropic superconductors.The

traditional approach starts from an anisotropic

Ginzburg–Landau or London free energy func-

tional and determines the desired quantity Q

by performing all the steps done previously

for the isotropic case. In the scaling approach

the desired quantity

Q is obtained by a rescal-

ing of the isotropic result Q.The scalingrules

are determined only once by a rescaling of the

anisotropic functional to an isotropic one

the theory via introduction of an anisotropic effec-

tive mass tensor into the Ginzburg–Landau or Lon-

don equations. In the conventional approach one

then repeats all the calculations which have been

done for the isotropic case before. Due to the ap-

pearance of additional parameters and the breaking

of spherical symmetry, the analysis becomes very te-

dious for the anisotropic problem.As a consequence,

new results become available first for the isotropic

case and in a subsequent step the case of cylindrical

symmetry, where the magnetic field is aligned with

the c-axis, is treated. Typically, only few results are

known for the general case of arbitrary field direc-

tion.In this section,we discuss a scaling approach to

the problem of anisotropy [176] which allows to gen-

eralize known results for isotropic superconductors

to anisotropic materials in a simple way, including

also the caseof an arbitrary direction of the magnetic

field with respect to the anisotropy axes; this new

scheme provides a simple and direct access to the

most general anisotropic results. In the following, we

first rescale the anisotropic problem to a correspond-

ing isotropic oneon the level of Ginzburg–Landau or

London equations and extract the scaling rules. In a

second step, these scaling rules are used to general-

ize the isotropic results to the anisotropic situation;

the two approaches are schematically illustrated in

Fig. 12.10.

Consider the Gibbs free energy (12.1) for an

anisotropic superconductor with masses m

= m

m, m

= M > m. As usual we denote the mass

anisotropy by "

= m/M < 1 and choose a coordi-

nate system with the external field H in the yz-plane,

enclosing an angle # with the y-axis, see Fig. 12.4.

We will make frequent use of the angle-dependent

anisotropy parameter "

, see (12.26). A first trans-

formation mapping (12.1) to an isotropic form has

been introduced by Klemm and Clem [126] and scal-

ing ideas have been used in calculations of the re-

versible magnetization and of the torque [222,223].

The important step in the construction of a general

scaling theory with a wide regime of applications is

the realization that for strong type-II superconduc-

tors with   1 ﬂuctuations in the magnetic field

can often be neglected [176].

In (12.1) the anisotropy enters only in the gauge

invariant gradient term and a simple rescaling of

the coordinate axes (we denote a quantity q in the

rescaled isotropic system by ˜q)

x = ˜x , y = ˜y , z = " ˜z , (12.161)

together with a scaling of the vector potential,

, A

, (12.162)

will render this term isotropic.As a consequence, we

obtain the scaling rules for the magnetic field,

, B

. (12.163)

Inserting this result back into the free energy func-

tional (12.1), the last two terms describing the mag-

netic field energy are transformed to

8





⊥



−2



⊥

· H

⊥



. (12.164)

534 G. Blatter and V.B. Geshkenbein

Hence, we have removed the anisotropy from the

gradient term but have reintroduced it in the mag-

netic energy term: in general it is not possible to

isotropize both terms in the Gibbs energy simulta-

neously. However, depending on the physical ques-

tion addressed, we can neglect ﬂuctuations in the

magnetic field. Problems such as vortex pinning or

vortex lattice melting involve the coherence length

 or the intervortex distance a

=(¥

/B)

1/2

as their

natural length scales; in strongly type II supercon-

ductors (with   ) or for large magnetic fields

(with a

< )thelengthscales and a

are small

compared to the scale  of variations in the magnetic

field.In suchsituationsthe magnetic field is uniform

on the natural length scale of the problem and we

can adopt a mean-field decoupling scheme, where

we first minimize the magnetic field energy G

with

respect to

B and then insert the resulting uniform

field back into the free energy. More rigorously, let

us consider the case  →∞or, equivalently, charge

e → 0. The coupling between the order parameter ¦

and the gauge field A is given by the gradient term

|[∇/i+(2e/c)A]¦ |

and vanishes in the limit e → 0.

The external magnetic field then merely fixes the av-

erage density of vortices.Hence the approach is exact

for the case of an uncharged superﬂuid.

Minimizing the magnetic field energy G

we ob-

tain

B =("H

, "H

, H

), corresponding to B = H in

the original system. Thus in the rescaled system the

magnetic field is reduced to

B = "

B (12.165)

as compared to the field in the original system. For-

mally, the deviation between the direction of B and

H (cf. (12.28)) is beyond the scaling approach, as

the uniformity of the magnetic induction requires

H  H

. On the other hand, proper transfor-

mation of the free energy (12.54) to the anisotropic

situation allows for a correct derivation of the results

(12.58) and (12.59), see [224]); hence, depending on

the situation, the scaling rules might be used even

beyond their formal regime of applicability.

Next, let us transform energy and temperature:

Since the volume scales as

V = "

V (12.166)

all energies E and temperatures T scale as

E = "

E , T = "

T . (12.167)

The latter can be easily understood from the

invariance condition on the Boltzmann factor,

exp(−

T)=exp(−G/T). An interesting subtlety

is the distinction between the microscopic temper-

ature entering the Ginzburg–Landau functional via

the parameter ˛ and the ﬂuctuation temperature T

entering in the Boltzmann factor: The appearance of

an additional temperature dependence in the “effec-

tive Hamiltonian” (= Ginzburg–Landau functional)

is a consequence of the partial summation over mi-

croscopic degrees of freedom in the partition func-

tion when going over from the microscopic formula-

tion in terms of electronic degrees of freedom to the

phenomenological description in terms of the order

parameter ¦ . According to the above derivation it is

only the ﬂuctuation temperature T determining the

statistical mechanics of the macroscopic wave func-

tion ¦ which is rescaled, whereas the microscopic

temperature determining the size of ˛ and hence of

, ,and remains unchanged.

Finally, when discussing vortex pinning in

anisotropic superconductors we will need the scal-

ing rule for the disorder: the latter is introduced into

the model via spatial disorder in the GL coefficient

˛(r) describing disorder in the transition tempera-

ture T

, and/or by spatial variation of the effective

mass m



(r) describing disorder in the mean free path

l. Usually, the disorder landscape is characterized by

a Gaussian distribution, e.g., ˛(r)=˛

+ ı˛(r)with

ı˛ =0andı˛(r)ı˛(r



) = 

ı(r − r



),and simi-

larly for m



(r)=m

0

+ ım



(r)withım



 =0and

ım



(r)ım





) = 

m 



ı(r − r



We first concentrate on the scaling of T

-disorder:

In the isotropized system the correlator reads

ı ˜˛(˜r)ı ˜˛(˜r



) = ı˛[r(˜r)]ı˛[r(˜r



)] =(

/") ı(˜r −

˜r



), thus the disorder strength 

scales as 

= " ˜

The second type of disorder is generated by the spa-

tial variation ofthe mean free path[10,18] and can be

described by a variation of the effective masses m(r)

and M(r).For a layered superconductor, the disorder

in m and M is due to disorder within the conducting

plane and between adjacent planes, respectively, and

thus in general the two need not to be the same af-

12 Vortex Matter 535

ter rescaling. The difference between the disorder in

m and M is only relevant in the small angle regime

|# | < ", since for angles larger than " the vortices

are redirected mainly along the c-axis after rescal-

ing and thus disorder in M can be neglected. Except

for this small angle regime, the disorder in the mean

free path can be treated as a scalar field and therefore

transforms in the same manner as the disorder in T

We then obtain the more general rule

 = " ˜ (12.168)

which is valid as long as the discreteness of the lay-

ered structure is not important. Note, that defining

the scale transformation according to (12.161), the

parameters  and  are not rescaled as the planar

coordinates are not affected by the transformation,

 =

 and  =

 . (12.169)

We are now in a position to set up the general scaling

rule for transferringresults from isotropic supercon-

ductors to anisotropic materials: Consider a uniaxi-

ally anisotropic superconductor (axis  z) character-

ized by the planar coherence length  and London

penetration depth ,theanisotropy", and the scalar

disorder strength  , in an applied magnetic field H

enclosing an angle # with the xy -plane, at a temper-

ature T.LetQ be the desired quantity for which the

isotropic result

Q is known.Then we obtain Q for the

anisotropic superconductor by the scaling rule:

Q(# , H, T, , , ",  )=s

Q("

H, T/", , ,  /") .

(12.170)

Typical scaling factors are s

= s

= "

for volumes, energies,actions,and temperatures,and

= s

=1/"

for magnetic fields.

We wish to point out that the scaling rule (12.170)

is not unique: Defined via a mathematical construc-

tion rendering the gauge invariant gradient term

in the Ginzburg–Landau functional isotropic. It is

clear that there exist alternative transformationrules

achieving the same goal. In particular, here we have

chosen a transformation which leaves the main pla-

nar parameters  and  ofthe superconductorinvari-

ant, with the consequence that volume, energy, tem-

perature, and disorder are rescaled. Another trans-

formation (e.g., the transformation used by Klemm

and Clem [126]) leaves the volume (and hence also

energy, temperature, and disorder) invariant. How-

ever, the planar parameters  and  are rescaled. The

important point to notice is that all these consistent

sets of scaling rules are equivalent to the originalrule

(12.170) (see also the discussion in [225] and [226]).

The scaling rule (12.170) can be used in vari-

ous ways: The most straightforward application is

the transformation of an expression

Q known for

isotropic superconductors to the result Q describ-

ing an anisotropic material and we give an example

below. But even in the absence of a formal expres-

sion for

Q, the scaling rule (12.170) provides useful

insight into the behavior of anisotropic materials;

e.g., assume a quantity Q (H) has been measured as a

function of field H  c, then the scaling rule (12.170)

predicts the complete angle and field dependence

Q(# , H),or conversely,allows foraconsistency check

of a measured data set Q(# , H) through an appropri-

ate data collapse.

Webeginwithanexampleofastraightforwardap-

plication of (12.170), illustrating how to transform a

known isotropic expression

Q to the anisotropic sit-

uation.Forthis demonstration we choose the single-

vortex elasticity "

; other examples will be discussed

below in the context of vortex lattice melting (an-

gular scaling of the melting line, see Sect. 12.7.2),

vortex pinning (Sect. 12.9), and vortex creep (see

Sect. 12.9.4).

The elastic energy of a single vortex is given by

(see Fig. 12.4)

F[u]=









(# )(@



)

+ "

⊥

(# )(@



)



(12.171)

Transformingthe in-plane tilt energy to the isotropic

system we obtain the relation



(# )

(ıu

)

ız



= " ˜"

(ı ˜u

)

ı ˜z



. (12.172)

Since  is invariant, ˜"

≈ (¥

/4)

= "

,where

we again concentrate on the short wavelength limit

of the elastic modulus. Furthermore, the amplitude

ıu

is not affected by the rescaling and therefore

ı ˜u

/ıu

= 1. On the other hand, the length ız



affected by the transformation (12.161): Let us con-

sider a segment of length l

directed along the z



-axis

536 G. Blatter and V.B. Geshkenbein

and let us transform this“longitudinal length” to the

rescaled system. There, we have

and

using (12.161) we obtain

= l

(cos

# +sin

# /"

With the definition (12.26) for the angle-dependent

anisotropy parameter "

, we find that longitudinal

lengths l

scale according to the rule

, l

 B , (12.173)

and therefore also ız



/ı ˜z



= "/"

.Thefinalexpres-

sionforthein-planeelasticitythenis"



= "

,in

agreement with the result (12.38) of the conventional

approach. When transforming the out-of-plane tilt

energy we should take care about the change of

angles due to the scale transformation: The trans-

formed vectors ı ˜u = ıu



(0, −sin# , cos# /")and

ı ˜z = ız



(0, cos # , sin # /") are no longer orthogo-

nal. Orthogonalizing, we obtain

⊥

(# )

(ıu



)

ız



= " ˜"

(ı ˜u ∧ ı ˜z)

ı ˜z



, (12.174)

and the final expression for the out-of-planeline ten-

sion then is "

⊥

(# )="

, in agreement with

(12.38).Here,wehaveusedthatı ˜z = ı ˜z



=("

/")ız



As an additional result,we obtain the scaling rule for

“transverse lengths”,

= "

, l

⊥ B ,

⊥

B , l

⊥ e

(12.175)

Next, let us use the scaling relation (12.170) to

predict the angular dependence of a quantity for

which we do not know an explicit expression but

only its field dependence along some particular di-

rection, usually along the c-axis. As a first simple ex-

ample we consider the scaling behavior of the in-

plane resistivity: the scaling factor for the in-plane

resistivity is s



= 1 and using (12.170) we obtain

(# , H)=("

H) ≈ (sin # H). In addition, for

# > ", after rescaling, the magnetic field is mainly

directed along the c-axis and thus the Lorentz force

is essentially independent of the directionof the cur-

rent in the plane. Going back to the original system,

one then expects the in-plane resistivity to be inde-

pendent of the angle between the magnetic field and

the current; these predictions are in good agreement

with the experimental findings of Iye et al.[227] (see

also [228]).In particular,assuming a slight misalign-

ment of the field away from the ab-plane direction,

the above arguments offer a natural explanation for

the angular independence of the dissipation for the

case where both the current and the magnetic field

are (nominally) aligned with the superconducting

planes [227]. Similarly, the anisotropy of the criti-

cal current density as measured by Roas et al. [66]

in YBCO and by Schmitt et al. [67] in BiSCCO thin

films exhibits all the features predicted by the scal-

ing rule (12.170): The latter predicts a dependence

of the in-plane critical current density j



on the an-

gle # in the form j



(# , H)=j

H), where j

(H)

denotes the critical current density measured in a

field H  c. In large magnetic fields the critical cur-

rent density j

(H) decreases with increasing field H.

Hence changing the direction of the magnetic field

leads to a dependence of the in-plane critical current

density j



(# , H)ontheangle# through the combi-

nation "

H, resulting in sharp maxima of j



(# , H)

when the field is aligned with the superconduct-

ing planes and a sharpening of these maxima with

increasing field amplitude H. A detailed discussion

of the angular dependencies of thermodynamic and

electromagnetic properties in anisotropic supercon-

ductorsas predicted by (12.170) and observed in var-

ious experiments can be found in [229].

We proceed with the more complex analysis of

the general resistivity tensor describing the electric

transport in the vortex state [230],

= 

(# , H)j

+ 

(# , H)j

, (12.176)

where 

(# , H)and

(# , H) denote the symmet-

ric and antisymmetric (in H) response tensors. The

basic idea then is to write this equation for the

isotropized system and then replace all quantities by

their anisotropic counterparts.In an isotropic system

the symmetry is broken by the direction ˜n =

H of

the magnetic field alone. The most general symmet-

ric and antisymmetric tensors then take the form

˜

(

H)= ˜(



+ ˜ (

H)˜n

˜n



˜

(

H)= ˜

(

H)"

ijk

˜n

. (12.177)

12 Vortex Matter 537

In order to generalize the relations (12.177) to the

(uniaxially) anisotropic situation we have to rescale

current densities, electric, and magnetic fields using

the relations

⊥

= j

⊥

= E

⊥

= "H

⊥

= "E

= H

(12.178)

which follow from the scaling laws for A, B,andthe

London formula for the current density. We start

from (12.176) rewritten for the isotropized system

and replace

E,and

H with the help of (12.178) by

their values in the original anisotropic system. The

two equations for the symmetric part then read

⊥

= ˜(

H)j

⊥

+ ˜(

H) ˜ (

⊥

(

⊥

·j

⊥

)

˜(

H) ˜ (

⊥

(12.179)

˜(



1+˜ (



˜(

H) ˜ (

(

⊥

·j

⊥

)

, (12.180)

and similar expressions are found for the antisym-

metric part describing the Hall effect,

=−˜

(

˜

(

, (12.181)

= ˜

(

−

˜

(

, (12.182)

˜

(

−

˜

(

. (12.183)

The relations (12.179)–(12.183) can be further pro-

cessed in two ways: Expressing the resistivity ten-

sor in terms of its isotropic counterpart we find

(˛, ˇ ∈{x, y})



˛ˇ

(# , H)=

s,iso

˛ˇ

H) ,



˛ˇ

(# , H)=

a,iso

˛ˇ

H) , (12.184)



˛z

(# , H)=



s,iso

˛z

H) ,



˛z

(# , H)=



a,iso

˛z

H) , (12.185)



(# , H)=



s,iso

H) . (12.186)

These results emphasize the modifications occurring

in going from an isotropic system to the uniaxially

anisotropic material characterized by the parameter

". In fact, the above derivation can be short-cut by

proper application of the scaling laws (12.178) for

current densities and electric fields, telling us that

each appearance of z is associated with one factor

1/".

In reality, however, the “equivalent” isotropic sys-

tem is usually not available.A more practical way to

express the above results then is in terms of quan-

tities measurable in the anisotropic system. This is

particularly convenient for the antisymmetric (Hall)

response where all coefficients can be expressed

through 

(H)(= −˜

(H)), the Hall coefficient

measured in the geometry with j ˆy, E ˆx,and

H ˆz,



(# , H)=−

H)"

ijk

. (12.187)

In particular



(# , H)=

sin #



(# , H)=

. (12.188)

Similarly, the symmetric response can be expressed

through the longitudinalresistivity

(H)(= ˜(H)),

measured with the magnetic field H aligned with

the material’s ˆz-axis, and the response 

(H)(=

˜(H)˜ (H)) measured in the force-free geometry

with j  H ˆx.

Regarding the regime of applicability of the scal-

ing rules (12.170) we point out that, in spite of start-

ing from a GL-typedescription,the scaling approach

is not limited to the regime near T

.In fact,the above

scaling rules can be obtained as well by starting from

the London equations which are valid throughout

the entire temperature regime. The scaling rules for

point-like disorder will not be changed as long as

the anisotropies in the penetration depths and in the

vortex core size remain the same.On the other hand,

extended pinning centers will be elongated (by the

538 G. Blatter and V.B. Geshkenbein

factor 1/")alongthec-axis and this might give rise

to enhanced pinning formagnetic fields aligned with

the c-axis, cf. Sect. 12.10.1 where pinning by colum-

nar tracks is discussed (the critical defect size along

the c-axis beyond which correlated pinning appears

is given by 

= ").Also,the scaling approach can be

used for the case of layered superconductors as long

as the discreteness of the structure is not important.

The crossover between quasi-2D and 3D anisotropic

behavior depends on the physical quantity of interest,

however, the regime where the anisotropic descrip-

tion is valid is usually large.

Finally, the scaling rule (12.170) clarifies the fol-

lowing features of anisotropic superconductivity:

First, the effect of anisotropy is to reduce the field

component in the superconducting planes and, sec-

ond, to enhance the effective strength of the pinning,

both favorable effects in view of technological ap-

plications of the new materials. On the other hand,

the anisotropy increases the temperature of thermal

ﬂuctuations, favoring phenomena such as thermal

depinning and melting of the vortex lattice, effects

which are scientifically very interesting, but rather

undesired in view of applications.

12.7 Statistical Mechanics

Thermal ﬂuctuations can have a dramatic effect

on the vortex system in type II superconductors:

strong ﬂuctuations produce vortex lattice melting

[11–13, 231] and trigger a decoupling transition

in layered superconductors [64, 71–76]. Also, they

change the constitutive B(H) relation near the lower

critical field H

[11]. In the presence of pinning,

thermal ﬂuctuations smear the pinning landscape

and lead to the depinning of the vortex lattice [23].

Furthermore, thermal activation of vortex segments

or vortex bundles produces an exponentially sup-

pressed but finite creep motion [14–17].

The strength of thermal ﬂuctuations is con-

veniently quantified through the dimensionless

Ginzburg number Gi which derives from a compari-

son of T

with the condensation energy in the coher-

ence volume. For a bulk superconductor [232] (we

set the Boltzmann constant to unity, k

=1),

Gi =



"









, (12.189)

while for a 2D thin film [233]

. (12.190)

Here, H

and "

=2"

(0)d are the Ginzburg–

Landau expressions for H

and "

extrapolated to

T → 0, cf. (12.12). The condition 1 − T/T

= Gi de-

termines the width of the critical region around the

transition temperature T

; note that this width in-

creases with field, Gi(H)=Gi

1/3

[H/H

]

2/3

.Incon-

ventional bulk superconductors the Ginzburg num-

ber is small, Gi < 10

−8

typically. Since Gi ∝ T

ﬂuctuationsgain dramaticallyinimportance in high-

superconductors; for YBa

we have Gi ≈

0.01 (

≈ 1000 Å, 

=12Å," ≈ 1/8, T

≈ 90 K),

while in layered Bi

CaCu

thermal ﬂuctuations

are predominantly of 2D character with Gi

∼ 0.03

(

≈ 1400 Å,d =15Å,T

≈ 90 K). The phenomena

of vortex lattice melting, layer decoupling, thermal

depinning, and thermal creep then are particularly

prominent in the copper-oxide based high-T

super-

conductors and to a somewhat lesser degree in other

anisotropic superconductors such as NbSe

and the

organic BEDT superconductors.

Below, we concentrate on the thermodynamic

phase transitions of vortex lattice melting and layer

decoupling. An early suggestion that the vortex lat-

ticemay undergoa melting transitionisdue toEilen-

berger [234]. Later, vortex lattice melting in 2D thin

films has been proposed and analyzed by Huberman

and Doniach and by Fisher [235,236]; early work

on bulk systems is due to Br´ezin, Nelson, and Thi-

aville [237]. Attention that this transition should be

prominent in high temperature superconductors has

been drawn by Nelson, by Houghton, Pelcovits, and

Sudbø, and by Brandt [11–13]. The first-order na-

ture of this transition has been conjectured in the

work of Br´ezin, Nelson, and Thiaville [237] and nu-

merical evidence for a sharp transition has been de-

rived from Monte-Carlo simulations [238–242].Sim-

ilarly,experimental work on bulk vortex latticemelt-

ing has proceeded in steps, with early work by Gam-

mel et al.[243].First experimental results hinting to-

wards a discontinuous transition have been reported

12 Vortex Matter 539

by Charalambous et al., Safar et al., and Kwok et al.

[36–38] and clear thermodynamic evidence through

the measurement of jumps in the magnetization and

in the entropy (latent heat) has been provided by Pas-

toriza et al., Zeldov et al., Welp et al., Schilling et al.,

and Junod et al. [39–43,244].

While melting in systems made from point-like

objects seems obvious, melting of a line crystal ap-

pears to be a more difficult concept — what is the el-

ementary segment of the line which should be identi-

fiedwith an independently ﬂuctuating degree of free-

dom? A simple answer is provided by the cage model:

consider a line trapped in the potential produced by

the other vortices in the lattice.The thermal displace-

ment u of the line involves tilt modes with energy

(u/L)

L where L is the length of the segment. On

the other hand, this displacement produces a shear

interaction with the vortices defining the cage (go-

ing beyond the nearest neighbors) with an energy

(u/a

)

L and comparing the two energies we

find the length L ≈

√

∼ a

of the ﬂuctuating

segment. In an anisotropic material with H ˆz the

line elasticity is reduced by the factor "

and hence

L ∼ "a

, in agreement with anisotropic scaling. Fi-

nally,wecan expect thecrystal to melt whenthe mean

thermal displacement u



1/2

becomes of the order

of the lattice constant a

; the equipartition theorem

tells us that u



∼ TL/"

∼ T/

√

∼ Ta

and hence the melting line follows from the relation

T/"

=const.; in an anisotropic material this is

modified to read T/""

=const.

A more rigorous argument starts from the Lon-

don free energy functional of the vortex system, see

(12.62). In the dense vortex system of a strongly type

II superconductor there is a large field regime ( 

 ) where we can neglect screening ( →∞)

and ignore the cutoff ; expressing all lengths in

terms of the lattice constant a



=(2/

√

1/2

(e.g.,



= s





) and including anisotropy via scaling (cf.

Sect. 12.6) we arrive at the form





}







,





· dx





− x



(12.191)

The statistical mechanics of the vortex system (as

given by the partition function over the free energy

(12.191)) then is completely determined by the pa-

rameter ratio ""



/T containing all the dependen-

cies on the field B and on the temperature T;the

melting line will be determined by some universal

constant derived from the dimensionless integral in

(12.191). Using the numerical results in [242] we ob-

tain a melting line of the form

=0.098 ""



=0.105 ""

=0.069 H

(T)







. (12.192)

Below we will further elucidate the various aspects

of vortex lattice melting in anisotropic and layered

superconductors.

Thermally induced layer decoupling is due to

phase ﬂuctuations in the superconductinglayers and

results in the destruction of phase coherence in the

direction perpendicular to the layers. Such a tran-

sition has first been proposed for the zero-field sit-

uation by Friedel [245], however, subsequent work

has shown that this transition is unfavorable [246].

Later,the concept of a decoupling transitionhasbeen

extended to the finite field situation (with B ˆz)

by Feigel’man et al. and by Glazman and Koshelev

[64,71,72]with the idea that ﬂuctuations of pancake-

vortices will help the transition. More refined dis-

cussions have been given by Daemen et al., by Frey,

Nelson, and Fisher, by Horovitz and Goldin, and by

Dodgson et al. [73–76].Work related to layer decou-

pling has been carried out on BiSCCO crystals [39,

247–249] and on MoGe/Ge multi-layers [250, 251];

however, while detailed and consistent experimental

results on vortex lattice melting are available today,

much less is known experimentally about the decou-

pling transition in layered superconductors.

Below we develop various ideas related to vortex-

lattice melting and layer decoupling. After a brief

review of ﬂuctuations in thin-film and layered su-

perconductors, we start with a discussion of the Lin-

demann approach to melting and decoupling, pro-

viding us with a quick overview over the various

melting lines in 2D superconducting films, layered,

and anisotropic superconductors. We proceed with

a more in-depth discussion of dislocation-mediated

melting in 2D thin-film superconductors. Further

progress beyond the Lindemann analysis can be