Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

500 G. Blatter and V.B. Geshkenbein

" < 1/50 in BiSCCO (depending on oxygen dop-

ing the anisotropy may be much larger with " of

order 10

−3

[25]). The anisotropy strongly promotes

thermal and quantum ﬂuctuations, since Gi ∝ 1/"

and Qu ∝ 1/". The above material parameters tend

to increase the importance of the ﬂuctuations in

the high-temperature superconductors.Whereas the

mean-field description was quite sufficient for the

understanding of the conventional low-temperature

superconductors this isno longerthe case for thenew

materials.In particular,the increase of Gi by roughly

six orders of magnitude implies that the vortex lat-

tice is melted over a large portion of the H–T phase

diagram; similarly, the increase of Qu by two orders

of magnitude renders macroscopic quantum effects

relevant. We wish to point out that these novel ef-

fects are not unique to high-temperature supercon-

ductors, they are present as well in the conventional

low-T

materials. However, it is the special set of ma-

terial parameters in the oxides which renders these

phenomena physically important and accessible to

experimental investigations.

The special material properties of the high-

temperature superconductors not only push the im-

portance of ﬂuctuations, they also tend to decrease

pinning in these materials. The weak pinning (small

) is not only a consequence of the small coher-

ence length  , but also follows from the absence

of generic extended pinning sites in these materi-

alssuchasprecipitatesorgrainboundariesoccur-

ring in many conventional superconductors. Again,

this circumstance is a consequence of the oxides be-

ing doped insulators rather than conventional met-

als, hence pinning centers are mainly provided by

point-defects, e.g., oxygen vacancies [26]. An im-

portant exception are the twin boundaries in YBCO

which provide extended pinning sites [27,28] upon

proper alignment of the magnetic field. Further-

more, in order to boost the critical current density

for technological applications strong pinning cen-

terscan beintroducedartificiallythroughirradiation

of the material with heavy ions producing columnar

tracks [29,30].

The generic weakness of pinning in the high-

temperature superconductors is interesting from a

theoretical point of view as it allows to treat the ef-

fects of quenched disorder perturbatively. In partic-

ular, weak pinning implies the existence of a well

definedstartingHamiltonianintheformofacon-

tinuumelastic description of the vortex lattice, upon

which effects due to disorder can be studied in a well

defined fashion. The dynamical behavior of the vor-

tex system in the presence of quenched disorder then

can be studied within the framework of the weak

collective pinning theory introduced by Larkin and

Ovchinnikov [8,10]. Furthermore, if pinning is weak

enough,the melting transition separating the vortex-

solid and liquid phases will be only little perturbed

by the presence of quenched disorder, allowing for

the observation of a generic melting transitionin the

vortex system.

The above discussion shows that we can expect

a wealth of novel phenomena in type II supercon-

ductors;atthesametimetheseshouldbeexperi-

mentally accessible and theoretically tractable in a

well defined fashion, thus allowing for a mutual ex-

change of experimental and theoretical results. On

the experimental side such novel phenomena include

the broadening of the resistive transition in a finite

magnetic field [31–33], the existence of a distinct ir-

reversibility line far below H

[34], often associated

with a vortex-glass transition [35],the appearance of

a first-order vortex lattice melting transition in high

quality crystals [36–43], the presence of giant creep

[44–46] even at temperatures far below T

[47,48],

a rapid decrease in the critical current density j

with increasing temperature [49], and the appear-

ance of quantum effects on approaching zero tem-

perature [50–52]. On the theoretical side the statis-

tical mechanics and the dynamics of individual vor-

tices and of the vortex lattice has been studied in ho-

mogeneous and in disordered environments. These

investigations have led to the postulation of new

phase transitions in the vortex system, such as the

vortex-lattice melting [11–13] andvortex-glass tran-

sitions [15,16].New vortexphases such as the entan-

gled and the disentangled vortex-liquids [11,53,54],

the vortex-glass [15–17], the Bragg-glass [19–21],

and the Bose-glass phase [55] have been proposed.

The presence of thermal ﬂuctuations leads to ther-

mal depinning of vortices [23]. The dynamical re-

sponse of the vortices is very different in these var-

12 Vortex Matter 501

ious phases and thus can be used for the charac-

terization of the new vortex-liquid [56] and vortex-

glass phases [15–17,19–21]. Also, the study of classi-

cal vortex motion has been extended to the quantum

regime [24,57].

A second source of novel phenomena is associ-

ated with the layered structure of the new oxides.

Whereas the YBCO compound still can be described

reasonably well within a continuum anisotropic

model, the layered Bi- and Tl-based compounds have

to be described by a discrete Lawrence–Doniach

model [58]. Superconductivity in these materials

then assumes features of quasi-two-dimensionality

and many experiments exhibit a characteristic Be-

rezinskii–Kosterlitz–Thouless (BKT) type behavior

[59,60].Dependingonthephysical situation,thesim-

ple rectilinear vortex has to be replaced by a more

complex object consisting of an array of 2D-pancake

vortices interconnected by (coreless) Josephson vor-

tices running parallel in between neighboring su-

perconducting planes [61–65]. The layered struc-

ture also introduces new features in the dynamical

response of the vortices due to the appearance of

intrinsic pinning and creep [66–69]. The statistical

mechanics of the vortex system is affected by the

layering via the presence of large (quasi-2D) ﬂuc-

tuations [70] and also through the appearance of

new phase transitions, e.g., a layer decoupling tran-

sition in a field H directed perpendicular to the lay-

ers [64,71–76]. When the field H is directed parallel

to the layers commensuration effects appear between

the crystal and the magnetic structure [77–80]; the

prediction of a decoupling transition in this geome-

try and an associated smectic transition [62,79–84]

is much disputed [85–88].

Much interest has concentrated on attempts to in-

crease the criticalcurrentdensity via the artificialin-

troduction of strong pinning centers (e.g., columnar

defects [29,30,89–91]) and the investigation of the

macroscopic properties of the new materials [92–95].

While research on these topics is driven by their

relevance for technological applications of high-

temperature superconductors,it is exciting to notice

that they bear a wealth of fundamental questions,

such as the substitution of the vortex-glass phase by

the Bose-glass phase in the case where the disorder

is correlated [55], or the relation of the macroscopic

behavior of a type II superconductor in a magnetic

field with ideas of self-organized criticality [96,97].

In order to give a theoretical description of these

very diverse phenomena one has to gather various

concepts and results from different branches ofmod-

ern theoretical physics, such as the theory of elas-

tic manifolds in quenched random media, polymer

physics, spin-glass theory, ﬂuctuational theory of

phase transitions, strongly correlated quantum sys-

tems,disordered quantumBose liquids,macroscopic

quantum tunneling, hopping conductivity in semi-

conductors, and self-organized criticality. The above

discussion then illustrates the richness and complex-

ity we encounter when dealing with the physics of

Vortex Matter.

The main philosophy followed below is to base all

the discussions on some “basic Hamiltonian” with

the requirement that it shall describe the vortex sys-

tem accurately. In particular, all the internal struc-

ture existing in the vortex system (e.g., the vortex

lattice) as well as the interactions present in the sys-

tem (e.g., between the vortices and the static dis-

order potential) shall be accurately described by

the model Hamiltonian. Examples for such “micro-

scopic Hamiltonians” used below are the (continu-

ous anisotropic) Ginzburg–Landau and London free

energy functionals, the discrete Lawrence–Doniach

model, and the continuum elastic free energy func-

tional for the vortex lattice. We emphasize that the

theory of Vortex Matter developed below applies

equally well to conventional low-T

and to uncon-

ventionalcopper-oxidehigh-T

superconductors,the

only requirement being that the order parameter de-

scribing the superﬂuid is a scalar quantity; given the

−y

-symmetry of the order parameter [98–100]

this condition is satisfied. In our terminology we

use the term “microscopic” when referring to length

scales ≥ , with the coherence length  denoting the

smallest scale in our problem. The calculation of 

itself is the subject of truly microscopic considera-

tions involving the solution of a very complicated

many-body problem; here, we will treat  as a phe-

nomenological parameter. Also, we will require our

starting Hamiltonians to describe a minimal model.

In particular, we will introduce the simplest possi-

502 G. Blatter and V.B. Geshkenbein

ble type of disorder in the system, usually described

by short-ranged Gaussian correlations. It turns out

that the physics described by such a minimal model

is already quite rich and accounts for a wealth of

experimental observations in a consistent manner.

Of course, starting out with these still very complex

Hamiltonians we cannot hope to develop exact an-

swers to our questions. We thus will have to resort to

approximate methods in dealing with the vortex sys-

tem, such as scaling estimates or perturbative anal-

ysis. The vortex system subject to quenched disor-

der, thermal and quantum ﬂuctuations, and possibly

driven by external forces is a complex object, and the

structure of the answers we will derive below is not

simple but involves many regimes where the behav-

ior of the system is different.

In what follows, we first discuss the basic frame-

work for the discussion of Vortex Matter, the

Ginzburg–Landau, London, Lawrence–Doniach and

continuum elastic theories.We discuss single vortex

properties in Sect.12.3,the vortexlattice in Sect.12.4,

pancake and Josephson vorticesin layered supercon-

ductors in Sect. 12.5, and the general scaling theory

used in the description of anisotropic material in

Sect. 12.6. Turning to the statistical physics of vor-

tex systems (Sect. 12.7) we discuss the various ﬂuc-

tuation regimes, the vortex lattice melting and de-

coupling transitions, and the nature of the resulting

vortex liquid phase.Wethen concentrate on the prop-

erties of vortex matter in the presence of quenched

disorder,startingwithanoverview(Sect.12.8) ondif-

ferent types of pinning, e.g. strong versus weak pin-

ning, pinning by uncorrelated/correlated disorder,

and a general discussion of vortex creep.In Sect.12.9

we present a detailed discussion of the theory of

weak collective pinning and creep: we analyze single-

vortex pinning and creep,its generalization to vortex

bundles, the phenomenon of quantum creep at low

temperatures and thermal depinning at high temper-

atures.Aspects of anisotropy andof the layered struc-

ture are dealt with as well.We proceed (in Sect.12.10)

with a discussion of strong pinning due to corre-

lated disorder (e.g.,due to columnar tracks) and then

concentrate on the effects of surface and geometri-

cal barriers (Sect. 12.11).Turning back to thermody-

namic aspects, but now in the presence of disorder,

we discuss the vortex-glass phases (see Sect. 12.12)

and the possibility ofa field-driven disorder-induced

melting transition at low temperatures.We close with

a discussion of Vortex Matter phase-diagrams. Un-

fortunately, this program leaves out a number of

prominent topics: among them are the c-axis trans-

port [101] and Josephson plasma physics [102,103]

in layered superconductors, the physics of moving

vortex systems [104], or the structure of individual

vortex lines in d-wave superconductors[105–107].

An introduction to the phenomenology of type II

superconductors can be found in [96,108,109]; sev-

eral aspects of Vortex Matter physics have been dis-

cussed in recent reviews [38,110] and the statistical

physics of dirty elastic manifolds has been reviewed

in [111,112].

12.2 Ginzburg–Landau and London Theories

The phenomenological description of supercon-

ductivity is based on the Ginzburg–Landau (GL)

free energy functional [15]: The quantum liquid

is described by a complex order parameter field

¦ (r)=|¦ (r)| exp[i'(r)].Furthermore,iftheﬂuidis

charged, as is the case in superconductors, the order

parameter field ¦ (r) couples to the vector-potential

field A(r) in a gauge invariant way. The free energy

functionals describing the superconductor take the

form

G[¦ , H]=F[¦ , B]−



H · B

4

F[¦ , B]=





˛|¦ |

|¦ |

(12.1)



=1















8



and have to be completed by the Maxwell equations.

The magnetic field B = ∇∧A is driven by the ap-

plied external field H. The Ginzburg–Landau (GL)

parameter ˛ =−|˛(0)|(1−T/T

)changessignatthe

transition temperature T

while ˇ assumes a con-

stant value. We choose the charge unit e to be posi-

tive, e > 0. The parameters m



,  =1, 2, 3, denote

the effective masses along the main axes of the crys-

tal. Here, we are mainly interested in isotropic and

12 Vortex Matter 503

in uniaxially anisotropic material described by effec-

tive masses m

= m

= m and m

= M and a mass

anisotropy ratio

= m/M < 1 ; (12.2)

while the isotropic case (m



= m,  =1, 2, 3)

mainly serves to introduce the basic ideas and con-

cepts,many of theinteresting strongly ﬂuctuating su-

perconductors, such as the copper-oxide or organic

materials [113], are layered crystals and hence uni-

axially anisotropic.

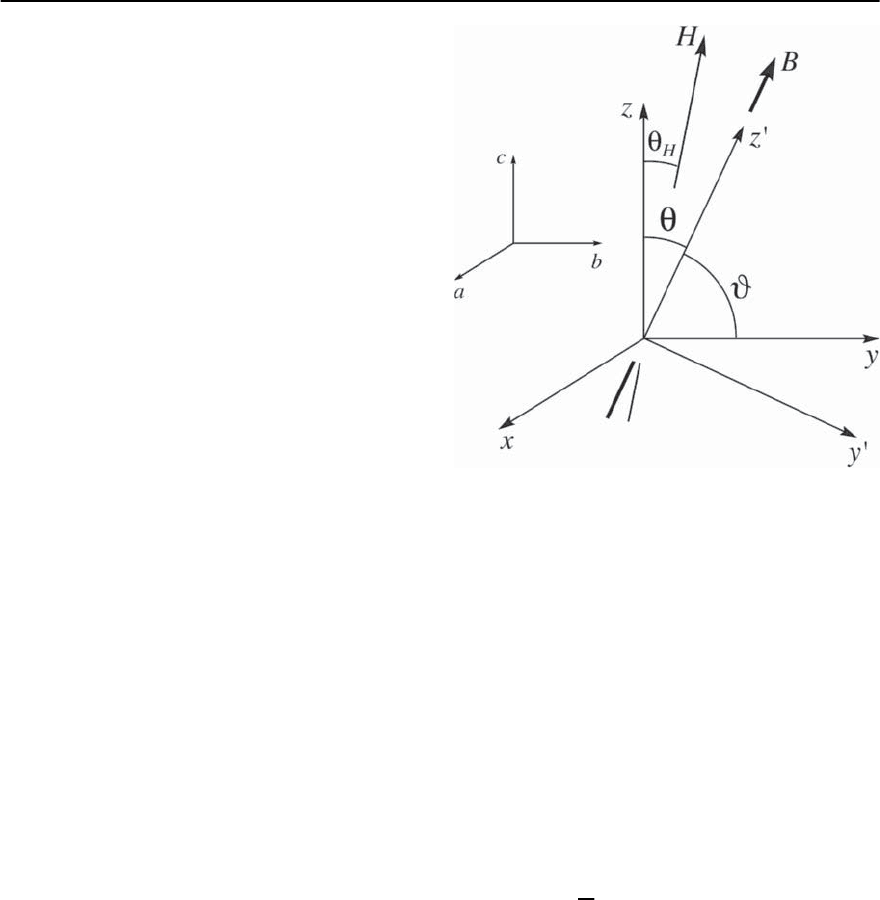
We choose a coordinate system with the z-axis

parallel to the axis of the material (the c-axis) and the

x and y-axes in the isotropic ab-plane, see Fig. 12.4.

An additional parameter appearing in the discussion

of anisotropic superconductors is the direction ofthe

external magnetic field H with respect to the crystal

axes: the external field H is chosen to lie in the yz-

plane and to enclose an angle 

with the c-axis (an

angle #

= /2−

with the ab-plane,see Fig. 12.4;

below we consistently use  and # = /2− to de-

note angles measured from the c-axis and from the

ab-planes). In the following, we will deal with the

isotropic case first and discuss the generalization to

the anisotropic situation whenever appropriate.

The Ginzburg–Landau energy (12.1) describes a

one-component superﬂuid and applies to conven-

tional (isotropic) s-wave superconductors.More gen-

erally, the functional (12.1) with a scalar order pa-

rameter field ¦ (r) also describes unconventional su-

perconductors with order parameters belonging to

other symmetry classes, with the constraint that the

symmetry representation is one-dimensional. E.g.,

in the high-T

superconductors the l =2angu-

lar momentum channel splits under the tetrago-

nal/orthorhombic crystal symmetry and the rele-

vant irreducible representation (of d

−y

symmetry)

is one-dimensional. The phenomenological descrip-

tion of Vortex Matter in type II superconductors de-

veloped below thus equally describes the situation in

conventional low-T

and in unconventional high-T

(copper-oxide) materials. In particular, the paramet-

ric dependence of the phenomenological parameters

entering the Ginzburg–Landau functional (12.1) on

the underlying microscopic parameters remain the

same, while numericals may be different. Examples

Fig. 12.4. Coordinate systems used in the description of

anisotropic and layered superconductors. The axes x, y,

and z are aligned with the crystal axes a, b,andc; c is the

axis of uniaxial anisotropy and the ab-plane contains the

superconducting layers.The magnetic field H liesin theyz-

plane and encloses an angle 

= /2−#

with the c-axis.

The induction B is in general not aligned with the mag-

netic field H and encloses an angle # with the ab-plane.

The coordinate system x



, y



, z



is aligned with the induc-

tion B and has a common x axis with the crystal system,



= x

where the d-wave symmetry of the high-T

’s leads to

strong (parametric) modifications of phenomeno-

logical results are rare; they appear in the context

of low-energy quasi-particle excitations in the gap

nodes, e.g., in connection with the field-dependence

of the low-temperature specific heat [114,115] scal-

ing like c

∝

√

H instead of the conventional behav-

ior c

∝ H, the low-temperature dependence of the

superﬂuid density n

(0) − n

(T) ∝ T [116], or the

non-linear Meissner effect (H)−(0) ∝ H [117],

which appears difficult to confirm experimentally,

though [118,119].

The homogeneous solutions of (12.1) are ¦

(normal state) and |¦

= |˛|/ˇ (superconduct-

ing state). The energy gain in the superconducting

state (˛ < 0) is due to the condensation energy

504 G. Blatter and V.B. Geshkenbein

/8 = ˛

/2ˇ,withH

the thermodynamic critical

field.In the inhomogeneous situation the variation of

(12.1) with respect to the fields ¦

∗

and A furnishes

the equations determining the spatial variations of

the order parameter ¦ = |¦ |exp(i') and the vector

potential A (we concentrate on the isotropic situation

here),





∇ +

2i



¦ +



1−

|¦ |

|¦



¦ =0, (12.3a)



|¦

|¦ |

∇∧(∇∧A)+A =−

2

∇' , (12.3b)

where ¥

= hc /2e ≈ 2.068 10

−7

Gcm

denotes the

ﬂux unit. Equation (12.3b) is conveniently rewritten

with the help of Amp`ere’s equation ∇∧B =(4/c)j

andprovidesuswithanexpressionforthecurrent

density

j =−

e

[¦

∗

∇¦ − ¦ ∇¦

∗

]−

∗

¦ A , (12.4)

=−

2e

|¦ |



∇' +

2



≡ −

2e

|¦ |

∇˜' ,

where we have defined the gauge-invariant phase

gradient ∇˜'. The characteristic lengths entering the

GL equations are the coherence length (T) and the

penetration depth (T),



(T)=



2m|˛(T)|

= 

1−T/T

, (12.5a)



(T)=

16e

|¦

(T)|

= 

1−T/T

, (12.5b)

determining, respectively, the scale of variations in

the order parameter ¦ and in the potential A (or

magnetic inductionB,current density j =(c/4)∇∧

B). In the following, we use the zero temperature val-

ues of the length scales  and  for the character-

ization of the superconductor. The thermodynamic

critical field H

is conveniently expressed through

these two basic scales,

√

2

. (12.6)

The maximal dissipation free current density the su-

perconductor can carry (the depairing current den-

sity) takes the value

√

6

; (12.7)

for larger current densities the kinetic energy of

Cooper pairs is larger than the energy gap  and

the pairs unbind.

The Ginzburg–Landau theory derives from an ex-

pansion in the small order parameter ¦ and hence

its applicability is restricted to temperatures close to

the superconducting transition temperature T

.Al-

ternatively, we can ignore spatial variations in the

order parameter and construct a free energy from

the kinetic energy of the currents j =(c/4)∇∧B

and the magnetic field energy B

/8.Theresulting

London free energy functional takes the form

[B]=

8





+ 

(∇∧B)



(12.8)

and is valid within the whole temperature range

0 < T < T

as long as the magnetic field does not

leadto a significant suppression of the order parame-

ter. For the strong type II superconductorswith large

Ginzburg–Landau parameter  = /  1weare

(mainly) interested in here, the London theory 12.8

provides a good approximation to the phenomeno-

logical description of superconductivity over a large

portion of the H-T phase diagram. The penetration

depth  appearing in (12.8) relates to the density n

of superconducting electrons via



(T)=

4n

(T)e

(12.9)

and the supercurrent density j canbewritteninthe

alternative forms

j =−

4



2

∇' + A



=−en





∇' +

2



, (12.10)

with v

denoting the superﬂuid velocity (in general,

the total current density j can pick up an additional

normal component j

, in which case we will denote

the supercurrent density (12.10) by j

). Variation of

(12.8) with respect to B provides us with the London

equation

12 Vortex Matter 505

[1 − 

∇

]B =0. (12.11)

Note that we distinguish between the extrapolated

zero-temperature parameter 

of the Ginzburg–

Landau theory, cf. (12.5b), and the zero-temperature

BCS expression [120] for this length,

(0) ≈ 1.41 

. (12.12)

A similar relation holds for the coherence length,

(0) ≈ 1.36 

.Belowwewillmakeuseofthein-

terpolation formula (T)

≈ (0)

/(1 − T

);

also, in going from a Ginzburg–Landau to a Lon-

don description we will use the definition |¦

(0)/4)(1 − T

)withtheT =0superﬂuidden-

sity equal to the electronic density n, n

(0) = n.The

above results apply to a clean material with a mean

free path l > (0); for a dirty material (l < (0)) we

have to replace 

→ ()

and 

→ 

/()

with  ≈ 1.17/,  = v

/2T

l;goingoverto

a dirty material increases the GL parameter  and

the superconductor becomes more strongly type II.

In unconventional superconductors described by a

scalar order parameter the GL parameters involve

additional angular averages over products involving

the structure of the gap function (k)(ofd

−y

sym-

metry in the copper-oxide high-T

superconductors)

and the Fermi velocity v

(k); these angular averages

depend on the details of the Fermi surface and gap

shapes and can modify the numerical factors relat-

ing the GL parameters,and hence also  and ,tothe

underlying microscopic parameters [121,122].

In an anisotropic material the London free energy

and the London equations take the form (in the vor-

tex frame of reference (x



, y



, z



), cf. Fig. 12.4)

[B]=

8





(12.13)



+(∇



∧ B) ·  · (∇



∧ B)



and

[B + ∇



∧ [ · (∇



∧ B)] = 0 ; (12.14)

here,

˛ˇ

= 

˛ˇ

+(

−



denotes the screen-

ing tensor with  and 

= /" the in-plane and

out-of-plane screening lengths and n



are the com-

ponents of the unit vector pointing along the crystal

axis (as seen from the vortex frame of reference; for

asystemwithB ˆz we have 

= 

= 

= "



and 0 else).

12.3 Vortex Lines

The Ginzburg–Landau equations (12.3a)–(12.3b)

admit topological solutions, these ﬂux lines, or

Abrikosov vortex solutions determine the rich phe-

nomenological phase diagram of type II supercon-

ductors with  = / > 1/

√

2. The cylindrical

vortex- or ﬂux-lines exhibit a non-trivial structure

in the order parameter field ¦ and in the magnetic

field B: the phase of the order parameter turns by

2 and drives a rotating current (note that with

the present definition of the charge (e > 0) the

phase field generating a vortex line rotates clock-

wise, ∇'

=−ˆz ∧ R/R

). Near the center of the

phase-turn the currents become large and suppress

the order parameter to zero, leading to a vortex

core of size . At the same time, the rotating cur-

rents generate a magnetic field and thus bind a

ﬂux to the vortex extending a distance  away from

the vortex core, where it saturates to the ﬂux unit

= hc /2e ≈ 2.068 10

−7

Gcm

To be more quantitative (see [96,108, 109] for a

standard derivation), let us integrate the cylindri-

cal current ﬂow (12.5), generated by a wave function

= |¦

|exp(−in ' )withn phase turns, along a loop



of radius R,





dl · j =2Rj

(R)=

2e

|¦

2



n −

¥ (R)



(12.15)

Here,¥ (R)=





dl·A is the ﬂuxpenetrating the loop.

The vortex solution (n = 1) then involves a circular

current ﬂow j

(R)=(2e|¦

/mR)[1 − ¥ (R)/¥

The apparent divergence of this current density upon

approaching the origin is cutoffthrough thesuppres-

sion of the order parameter ¦

on the scale R ∼ 

as the current density j

becomes of the order of

the depairing current density j

; a convenient expres-

sion for this suppression as obtained via a variational

Ansatz [123,124] has the form

|¦

(R) ≈

+2

|¦

. (12.16)

Going to large distances, the screening currents as-

semble a ﬂux ¥ (R)oftheorderoftheﬂuxunit¥

on a scale R ∼ ; increasing R beyond  the drive

506 G. Blatter and V.B. Geshkenbein

∝ [1 − ¥ (R)/¥

] vanishes and the current density

drops to zero rapidly: this is the phenomenon of

transverse screening.

The precise shape of the trapped magnetic field

B(R) follows from the London equation (12.11) com-

pleted with a source term ¥

ˆz ı

(R) describinga vor-

tex line placed at the origin,

[1 − 

∇

]B = ¥

ˆz ı

(R) ; (12.17)

integration provides us with the magnetic field (for

R > )

B(R)=

ˆz

2



R/



(12.18)

()istheMacDonaldfunction,K

(  1) ∼

−ln; K

(  1) ∼ e

−

√

). The kinetic energy

of the screening currents j

gives rise to the line en-

ergy 

of the vortex,











∇ +

2i





≈



|¦









4







. (12.19)

The prefactor



4



(12.20)

defines the basic energy scale of Vortex Matter. The

above estimate for the line energy involves only the

kinetic energy of the currents and has to be com-

pleted by the magnetic field- and normal-core con-

densation energies; the magnetic energy contributes

aterm"

/2 and a similar term C"

with C anumer-

ical small compared to the logarithm ln(/ )hasto

be added for the core.The numerical solution of the

Ginzburg–Landau equation (with   1) provides

the result [125]





4









+0.497



(12.21)

(note that the constant in (12.21) differs from usual

values cited in the literature [96,108,109]).Inuncon-

ventional d-wave superconductors the currents and

magnetic fields appearing in the vortex core can in-

duce other order parameter components,e.g. of the s

or d

-type[105],however,their impact on thevortex

shape is usually small.

These topological solutions of the Ginzburg–

Landau equations are crucial in determining the

(mean-field) H–T phase diagram of a type-II super-

conductor: At small magnetic fields the supercon-

ductor is strong enough to expel the magnetic field

and this defines the Meissner–Ochsenfeld state. In-

creasing the field, the free energy of the vortex state

drops below that of the Meissner state when the vor-

tex line energy 

matchesupwiththemagneticen-

ergy ¥

H/4 and we find the lower critical field H

(see Fig. 12.1),

4

4







+0.497



. (12.22)

Going beyond H

, vortices rush into the supercon-

ductor to form a triangular lattice (named after

Abrikosov [3]) with the lattice constant a



and the

density n

= a

−2

determined by the induction B,





√



1/2





1/2

and a

. (12.23)

In a large external field H the vortex cores start over-

lapping when a

≈  and superconductivity disap-

pears above the upper critical field H

2

, (12.24)

giving way to the normal-metallic phase.

In an anisotropic material the line energy depends

on the angle # between the vortex and the ab-plane

of the material [126,127], see Fig. 12.4,



(# )="









, (12.25)

with the angle-dependent anisotropy parameter

= "

cos

# +sin

# (12.26)

and "

=(¥

/4)

,  denoting the in-plane screen-

ing length. The lower critical field H

is obtained

by minimizing the Gibbs free energy G;atsmall

values of B we have G ≈ B

/8 +(B/¥

)

(# )−

(BH/4)cos(# − #

), where # (#

) denotes the an-

gle enclosed by B (H)andtheab-plane. Minimizing

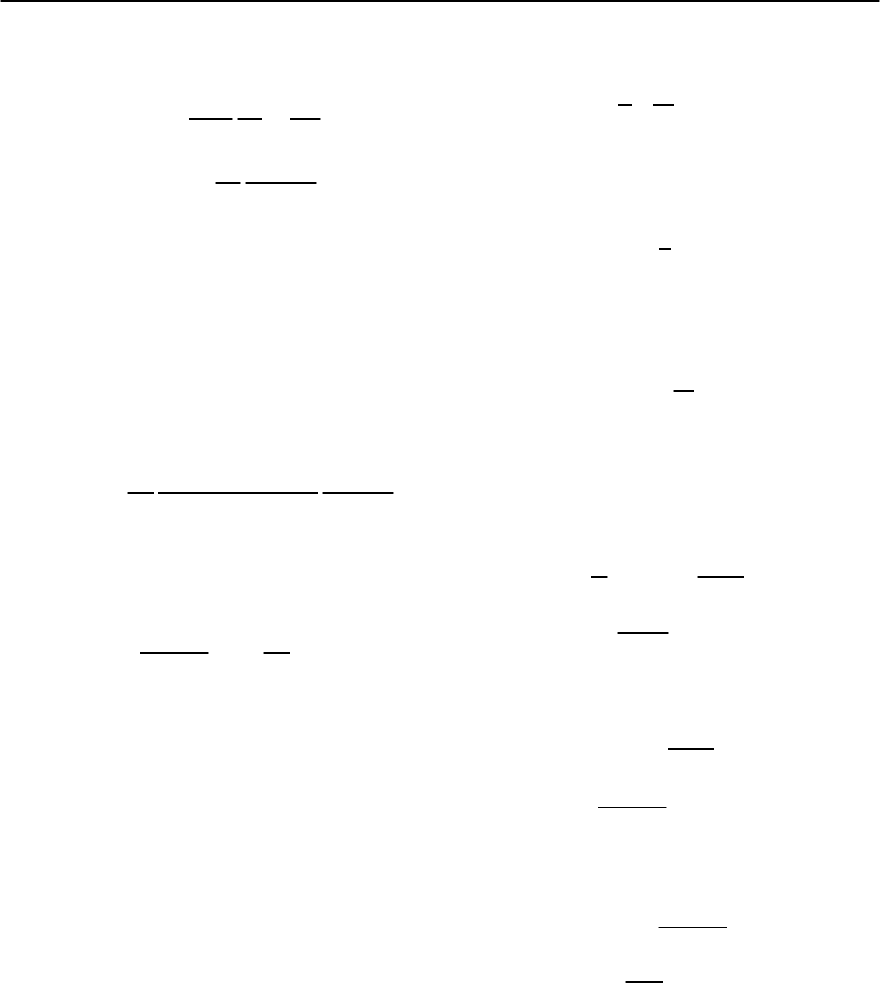
12 Vortex Matter 507

G with respect to B

and B

and setting B to zero we

find the lower critical field [126]

(

) ≈

4







= H



ln(/"

)

ln()

, (12.27)

where 

denotes the angle enclosed between the

magnetic field H and the c-axis, hence "



cos

+ "

sin

.Theangle# at H

is given

by tan

# = "

tan

and we can reexpress "

(1 + "

tan

)/(1 + "

tan

) in (12.27). Min-

imizing G with respect to # we obtain the relation

between #

and # away from H

(note that # < #

and the vortex lines tend to align with the supercon-

ducting planes),

sin(#

− # )=

(1 − "

)sin# cos#

ln(/"

)

ln()

(12.28)

The expression for the upper critical field follows

from the anisotropic vortex core with dimensions 

and "

 along x and y



and takes the form

2"



= H

. (12.29)

For large fields we have to replace the log-

arithm ln(/"

) in (12.28) by its counterpart

ln[˛H

(# )/B)

1/2

] (cf. (12.54) below); for H 

the misalignment between the magnetic field

H and the induction B becomes small.

12.3.1 Elasticity

Within a phenomenological or statistical mechanics

description a vortex is usually modeled as an elastic

string which, when compared with a point-like ob-

ject, exhibits additional static and dynamic proper-

ties due to its one-dimensional extended nature. The

elastic response of the vortex line is determined by

its line tension: We consider a vortex in an isotropic

material aligned with the z-axis of our coordinate

system. The elastic energy of a deformed vortex is

determined by the increase of the vortex length,



dz 

[1 + (@

]

1/2

−1

≈







, (12.30)

where u(z)=(u

, u

) denotes the displacement field

of the vortex. In an isotropic material the long wave-

length line tension "

is equal to the line energy 

= "







+0.497



. (12.31)

In general, however, the vortex line tension is dis-

persive; solving the London equation for a deformed

vortex s(z)=[u(z), z ],

[1 − 

∇

]B = ¥



(r − s(z)) (12.32)

(conveniently done in Fourier space) and inserting

the result back into the London functional (12.8)

rewritten in the form F

=(1/8)



rB(r)[1 −



∇

]B(r) we obtain the energy of the distorted vor-

tex line

[s(z)] =



dzdz





du(z)

, 1



(12.33)



du(z



)



, 1



V[s(z)−s(z



)] ,

with the interaction potential between vortex seg-

ments

V(r)=4



(2)

ikr

V(k) ,

V(k)=

−

1+

. (12.34)

Expanding (12.34) to second order in the distortion

u(z) one arrives at the dispersive line tension [173],

) ≈ "





1+



1/2

(12.35)

+ "



ln(1 + 

)

1/2

This expression is usually dominatedby the first term

with its weak logarithmic dispersion,"

> 1/) ≈

ln(1/k

). The result (12.36) is easily understood

in the following terms: the line energy (12.19) of a

vortex mainly arises from the currents circulating

508 G. Blatter and V.B. Geshkenbein

the core, which usually are cut off at short (the core

radius ∼ ) and long (the screening length ∼ )

distances. In a short wavelength distortion only cur-

rents on scales smaller than 1/k

are distorted and we

have to replace the cutoff  by 1/k

.Similarly,the sec-

ond term originates from distortions in the magnetic

field: a short wavelength distortion (k

> 1/)in-

volves only a fraction 1/k



of the total field energy

/2 and we obtain the strongly dispersive electro-

magnetic component of the line tension. In (12.19)

wehaveignored afurther term accounting for thede-

formation of the vortex core which is dispersive on

the scale .Below we will deal with various phenom-

ena involving short wavelength distortions k

∼ 1/L

of the vortex line with  < L   (e.g., thermal

ﬂuctuations with L ∼ a

  at high fields or vortex

pinning). In this case we will often drop the logarith-

mic correction ln(1/k

) in the line tension and use

the approximation "

∼ 1/L) ≈ "

In an anisotropic material the angular depen-

dence of the vortex line energy produces two dif-

ferent angle-dependent elasticities "



(# )and"

⊥

(# )

for in- and out-of-plane distortions: we start with

the energy 

(L, # )=L

(# ) of a vortex segment of

length L enclosing an angle # with the ab-plane (see

(12.25)) and determine the increase in energy due to

a symmetric distortion Lı on a distance 2L;

ı

@

ıL +

@

ı# +



(ı#)

. (12.36)

An out-of-plane tilt by an angle ı = ı# increases

the length of the segment by ıL ≈ L(ı#)

/2; simi-

larly,an in-plane distortion gives rise to an additional

length ıL ≈ L(ı)

/2 and produces a change in #

determined by tan(# + ı#)=L sin # /[(L cos # )

(Lı)

]

1/2

,henceı# =−(tan# )(ı)

/2. The out-

of-plane and in-plane elasticities are defined by the

relations

⊥

L(ı#)

@

ıL +



(ı#)



L(ı)

@

ıL +

@

ı#; (12.37)

a few algebraic manipulations then produce the ex-

pressions for the out-of-plane and in-plane elastici-

ties (we ignore logarithmic corrections)

⊥

≈

and "



≈

. (12.38)

A second contribution to the tilt modulus arising

from electromagnetic interactions is discussed in

Sect. 12.4.1.

12.3.2 Dynamics

A number of forces attack the vortex line (here par-

allel to ˆz) in a type-II superconductor in the dy-

namical situation andtheircorrectaddition(without

omissions or double counting) is far from trivial. We

distinguish between hydrodynamic forces arising at

large distances and forces due to quasi-particle scat-

tering in the vortex-core region;the most well known

example for a vortex equation of motion is given

through the compensation of the Lorentz force(from

hydrodynamics) and the Bardeen–Stephen friction

force (from dissipative scattering in the vortex core)

[5],

+ f

j ∧ˆz − 

=0, (12.39)

resulting in a vortex velocity v

transverse to the

driving current density j; the viscousdrag coefficient



as derived by Bardeen and Stephen reads



2c





, (12.40)

where 

denotes the normal-state resistivity of the

material. In order to discuss the limitations of this

equation and the appearance of various other forces

attacking the individual vortex line, we consider a

simple phenomenological model providing us with

some insight into the origin of the vortex equa-

tion of motion; an accurate derivation starting from

microscopic theory has been given by Kopnin and

Kravtsov [128],see also [129,130].We model the vor-

tex core as a sharp normal cylinder with an elec-

tron density n

which in general may differ from the

asymptotic density n. The average force density act-

ing on the electronic system involves contributions

from the Lorentz force j ∧B/c, the electric field force

enE, and the scattering term mn

f (B/H

)/

the carrier velocity in the vortex core and 

is the

transport relaxation time),

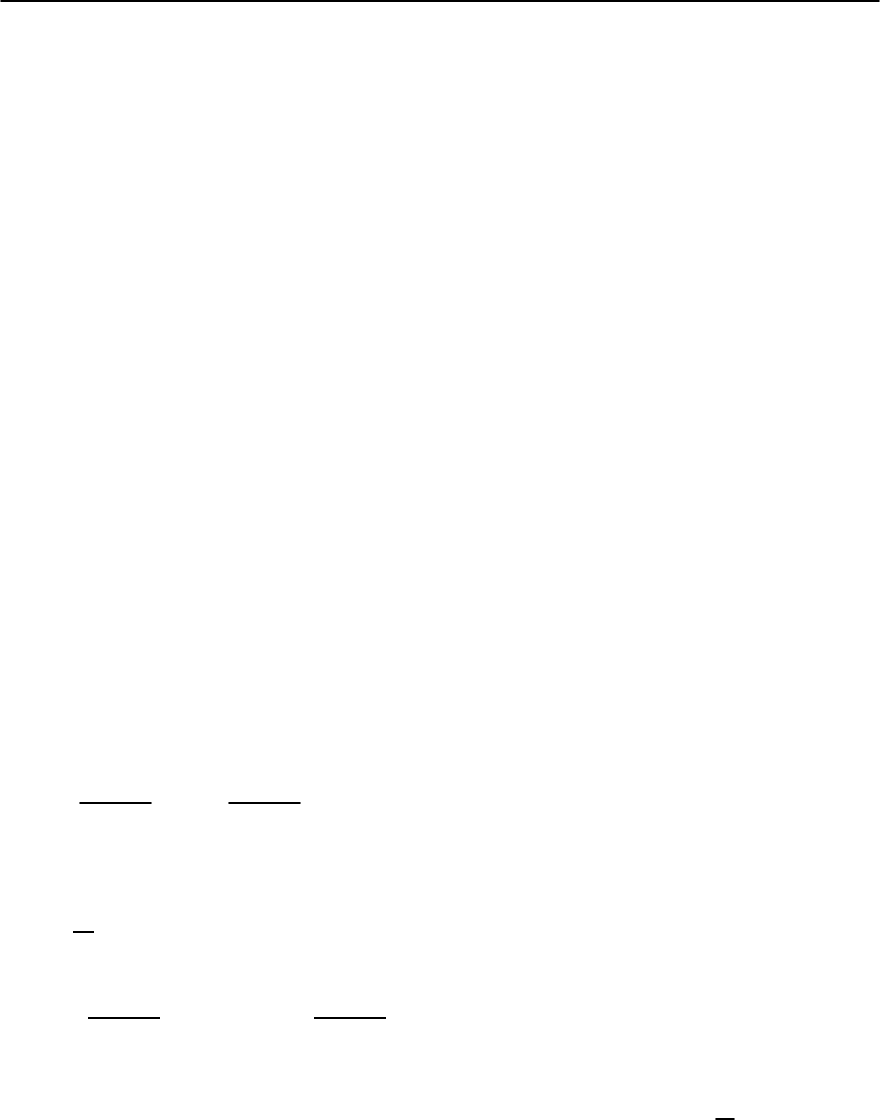
12 Vortex Matter 509

j ∧ B/c + enE − mn

f (B/H

)/

=0. (12.41)

The normal metallic state is uniform and we have

= n, v

= v,andf =1;solvingtheequation

of motion (12.41) for the current density (velocity)

j = env we obtain the well known expressions for

the longitudinal and transverse (Hall) conductivi-

ties in the normal state, 



= 

/(1 + !



)and



⊥

= 



/(1 + !



), with the normal state con-

ductivity 

= e

n

/m and the cyclotron frequency

= eB/mc.

On the other hand, the superconducting state is

inhomogeneous and scattering is limited to the vor-

tex cores; correspondingly we introduce the reduc-

tion factor f ≈ B/H

. Furthermore, the electric

field is now determined by the vortex velocity via

E = B ∧ v

/c. Usually, the carrier density inside the

core is assumed to be equal to the asymptotic elec-

tron density, n

= n, and we can write the transport

current density in the form j = en

= en

, i.e.,

the current density ﬂows through the system in a ho-

mogeneous manner (n

and v

denote the superﬂuid

density and its velocity). The force equation (12.41)

then relates the carrier velocity v

in the core to the

vortex velocity v

= !



− v

) ∧ˆz , (12.42)

with !

≈ eH

/mc (in a clean material, !

≈



/2m

≈ 

corresponds to the level split-

ting of the quasi-particles trapped in the vortex core

[131]). Solving for the velocity v

we obtain



1+!



ˆz ∧ v



1+!



, (12.43)

and taking the cross product of (12.43) with

en(¥

/c)ˆz we obtain the forceequation [132]

j ∧ˆz = 

+ ˛

∧ˆz , (12.44)

with the response parameters



= n



1+!



and ˛

= n



1+!



(12.45)

consistent with the result derived from a micro-

scopic analysis [128]. The two terms in (12.44) then

push the vortex either in a direction transverse to

the driving current (dissipative motion governed

by 

)ordragthevorticesalongthecurrentdi-

rection (Hall motion governed by ˛

). The result-

ing vortex motion produces longitudinal and trans-

verse (Hall) ﬂux-ﬂow conductivities of the form



FF

=(H

/B)

/(1 + !



)and

⊥FF

= !





FF

Usually,the parameter !



is small,!



 1,i.e.,

themeanfreepathl isnot large,l  "

/ ≈ (k

);

we then recover the dissipative equation of motion

(12.39). The vortex exhibits a fast (v

≈ v



)

motion transverse to the ﬂow j = en

.Theresult-

ing large electric field E ≈ v

/c in the core re-

gion provides the necessary drive to push the nor-

mal current density j

through the core such that

the overall current ﬂow is divergence free [123],

∇·(j

) = 0.The frictioncoefficient agrees withthe

expression derived by Bardeen and Stephen [5]; the

ﬂux-ﬂow conductivity is given by the well known ex-

pression 

FF

=(H

/B)

(note that corrections to

the Bardeen–Stephen result become important near

the transition temperature and for high magnetic

fields [133,134]).

Expressions similar to (12.45) are obtained in the

quasi-classical analysis of ﬂux ﬂow in d-wave super-

conductors [135]; as expected the results keep their

parametric form but involve additional angular av-

erages of the gap structure over the Fermi surface, at

least for moderate disorder. Modificationsdue to the

gap nodes appear in very clean material only (the

so-called “superclean” limit with a large mean free

path l > "

/, see below); these are, an unusual

magnetic-field dependence of 

FF

∝ B

−3/2

,univer-

sal limits (independent of 

) of the ﬂux-ﬂow conduc-

tivities for low temperatures and fields, and a resid-

ual (in the limit 

→∞) finite dissipation due to

Landau damping on zero-frequency vortex modes.

In an anisotropic material the viscous drag coef-

ficients depend on the direction # of the ﬂux line

and on the direction of motion: the two effects of

an angle-dependent vortex core size "



and an

angle-dependent electronic mass m

for the out-

of-plane (electronic) motion along y



compete with

each other and produce the dissipative response co-

efficients for the moving vortex in the form





= "



, 

⊥



, (12.46)