Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

11 Universal Properties of Cuprate Superconductors 479

tent with the scaling relation d

/dT



T=0

∝ ı



(

D−2z

)

(see (11.46)). Indeed at 2D–QSI criticalitywith z =1,

d

/dT



T=0

tends to a constant value and diverges

close tothe3D–QSNcriticalpointfor z > 3/2.Unfor-

tunately, the data does not extend sufficiently close

to the overdoped limit to provide reliable estimates

of the exponent combination



(

3−2z

)

Provided that the linear T-term of 1/

(

)

in the

zero temperature limit exists, the scaling relations

(11.38) and (11.38) yield close to quantum criticality

the universal relation





(0)



(T)





T=0

= y



y=0

, (11.79)

where D =2andD = 3 for the 2D–QSI and

3D–QSN transition, respectively. In Table 11.1 we

collected additional estimates for various cuprates

and doping levels. The rise of the magnitude

of T

d/dT

(



(ı, 0)/

(ı, T)

)



T=0

with increasing

doping level reﬂects the 2D–3D-crossover in the scal-

ing function Y

. Noting that most compounds are

close to optimum doping it is not surprising that the

listed values scatter around –0.61,the value of nearly

optimally doped La

2−x

CuO

Before turning to the substitutiontuned quantum

transitions it is useful to express the doping depen-

dence in the interpolation formula (11.77) in terms

of the transition temperature. This is achieved by

invoking the empirical correlation 11.2 between T

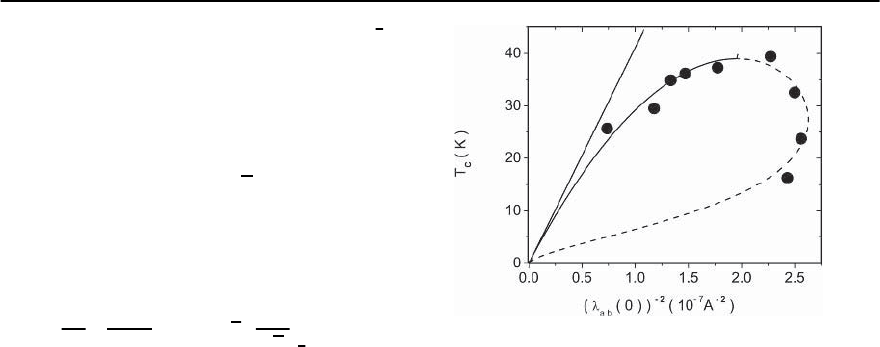
and doping concentration x. In Fig. 11.22 we dis-

played the resulting Uemura plot, T

versus 1/

(

)

for La

2−x

CuO

in terms of the solid and dashed

curves, resembling the outline of a ﬂy’s wing. The

solid curve marks the ﬂow from T

(

)

to the 2D–

QSI critical point and the dashed one the ﬂow to

3D–QSN criticality.Thedotted line indicates the uni-

versal 2D-behavior (see (11.40)) and (11.68)). For

comparison we included the experimental data of

Panagopoulos et al. [9] and Uemura et al. [83]. Al-

though the data does not attain the respective crit-

ical regimes, together with the theoretical curves,

they provide a generic perspective of the ﬂow to 2D–

QSI and 3D–QSN criticality.Indeed, convincing evi-

dence forthese ﬂows emerges from the SR data dis-

played in Fig. 11.23 for Y

0.8

0.2

(Cu

1−y

7−ı

0.8

0.2

-123), Tl

0.5−y

0.5+y

1−x

(Tl-

Fig. 11.22. T

versus 1/

(

)

for La

2−x

CuO

. •:experi-

mental data taken from [9,83].The solid and dashed curves

result from the empirical law (11.2) and the interpolation

function (11.77) with T

(

)

= 39.8 K and the parameters

listed in (11.78). The solid line indicates the ﬂow from op-

timum doping to 2D–QSI criticality and the dashed line to

the 3D–QSN critical point

1212) [103] and TlBa

CuO

6+ı

(

Tl-2201

)

[104]. In

analogy to Fig. 11.22,the solid curves mark the ﬂow

from T

(

)

to the 2D–QSI critical point and the

dashed curves the approach to 3D–QSN criticality.

Additional confirmation of thisﬂow emerges from

Fig. 11.24, showing the condensation energy versus

hole concentration p for Y

0.2

7−ı

taken

from Tallon and Loram [105]. The solid and dashed

curves are (11.51), in terms of

−E

(

T =0

)

∝ ı

(z+D

)

∝



p − p



∝ T

−E

(

T =0

)

∝



− p



5/2

∝ T

5/2

, (11.80)

with

(

z + D

)

/z =3and

(

z + D

)

/z =5/2, the values

appropriate for the 2D–QSI (see (11.65)) and 3D–

QSN (see (11.67)), respectively.

A generic ﬂow to the 2D–QSI critical point also

emerges from the plot 

(

)

versus 





displayed

in Fig. 11.25 for YBa

7−ı

,La

2−x

CuO

and

CaCu

at various doping levels. An empir-

ical, nearly linear, correlation between these quan-

tities has been proposed by Basov et al. [106]. From

the scaling relation (11.58) it can be seen that the sys-

tematic rise of 

(

)

with decreasing 





,tuned

by decreasing dopant concentration and the asso-

ciated rise of the anisotropy 

,againreﬂectsthe

ﬂow to 3D–QSI criticality. The straight line marks

480 T. Schneider

Table 11.1. Estimates for T

d/dT

(



(

)

/

(

))



T=0

derived from the experimental data of: slightly underdoped

HgBa

8+ı

, slightly overdoped HgBa

CuO

4+ı

[100], under-, optimally- and over-doped La

2−x

CuO

[9],

CaCu

8+ı

[101],Y

0.94

0.6

,YBa

1.925

0.075

and Y

1.9

0.1

[102]



(

)

(A) T

(K) T





(ı,0)



(ı,T)





T=0

HgBa

8+ı

1770 135 –0.59

HgBa

CuO

4+ı

1710 93 –0.65

1.9

0.1

CuO

2800 30 –0.49

1.85

0.15

CuO

2600 39 –0.61

1.8

0.2

CuO

1970 35 –0.72

1.78

0.22

CuO

1930 27.5 –0.72

1.76

0.24

CuO

1940 19 –0.94

CaCu

8+ı

2600 91 –0.61

0.94

0.06

1361 88 –0.51

YBa

1383 81 –0.58

YBa

1.925

0.075

1521 74 –0.61

YBa

1.9

0.1

1593 72 –0.63

Fig. 11.23. T

versus 

∝ 

−2

(

)

for Y

0.8

0.2

(Cu

1−y

7−ı

0.8

0.2

-123),

0.5−y

0.5+y

1−x

(Tl-1212) [103]

and TlBa

CuO

6+ı

(Tl–2201) [104].

The solid and dashed curves result from the em-

pirical law (11.2) and the interpolation function

(11.77). The solid curves indicate the ﬂow from

optimum doping to 2D–QSI criticality and the

dashed curves to the 3D–QSN critical point

the asymptotic behavior La

2−x

CuO

for z =1and

≈ 24m(§cm)

3/4

.Since§

depends on the crit-

ical amplitudes 

0,0

, 

ab,0

(

)

, 

and the thickness

((11.58) and (11.59)), its value is unique within

afamilyofcuprates.§

≈ 24m(§cm)

3/4

follows

from 

0,0

≈ 1.63, 

≈ 2 (see Fig. 11.1), d

≈ 6.6A,



≈ 1and

ab,0

(

)

≈ 736 A (see (11.78). Al-

though the experimental data is still quite far from

the underdoped limit, the ﬂow to 2D–QSI criticality

with family-dependent values of §

can be antici-

pated. This differs from the mean-field prediction

for bulk superconductors in the dirty limit and lay-

ered BCS superconductors,treated as weakly coupled

Josephson junctions (see (11.60) and (11.61)), where

∝ T

−1/2

. Moreover, as the optimally doped and

underdoped regimes are approached, systematic de-

viations from the straight line behavior appear,indi-

cating the ﬂow to 3D–QSN criticality (see (11.63)).

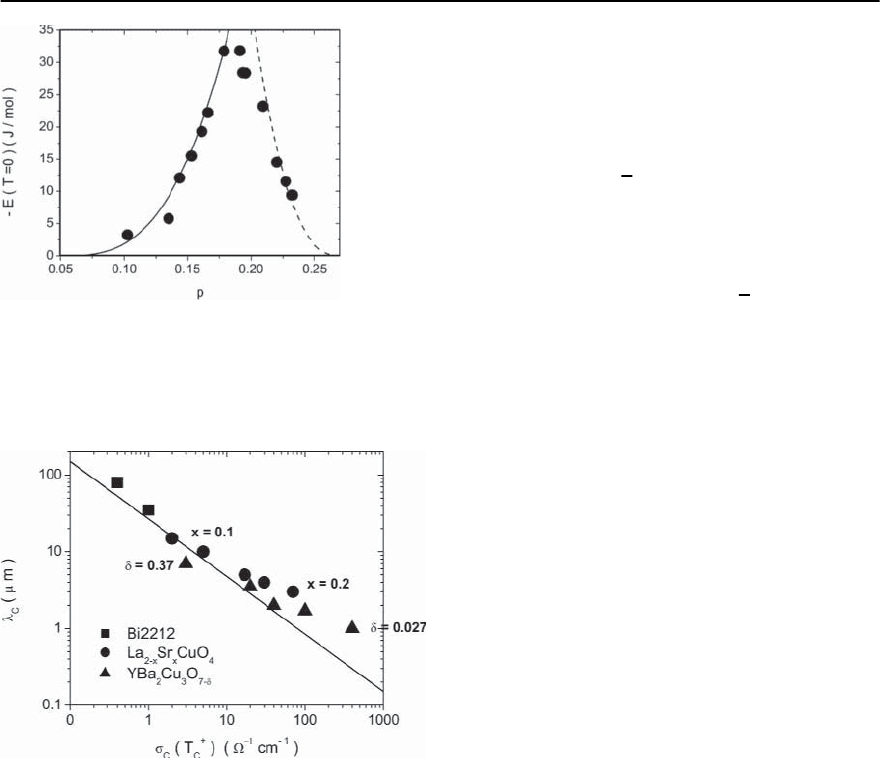
11 Universal Properties of Cuprate Superconductors 481

Fig. 11.24. Condensation energy −E

(

T =0

)

versus hole

concentration p for Y

0.2

7−ı

. The experimen-

tal data is taken from Tallon and Loram [105]. The solid

and dashed lines are (11.80), indicating the approach to

2D–QSI and 3D–QSN criticality

Fig. 11.25. 

(

)

versus 





for YBa

7−ı

(),

2−x

CuO

(•) [107] and Bi

CaCu

() [108].The

straight line is (11.58)with z =1and§

≈ 24m

(

§cm

)

3/4

theestimateforLa

2−x

CuO

According to the empirical correlation between

and anisotropy 

(see (11.3 and Fig. 11.2), the

initial value of the dopant concentration determines

whether the ﬂow leads to 2D–QSI or 3D–QSN criti-

cality. For initially underdoped cuprates, the rise of



, tuned by the doping induced reduction of T

,di-

rects the ﬂow to 2D–QSI criticality. Conversely, in

initially overdoped cuprates, the fall of 

to a finite

value drives the ﬂow to the 3D–QSN critical point.As

the nature of the quantum phase transitions is con-

cerned we have seen that the 2D–QSI transition has

a rather wide and experimentally accessible critical

region.For this reason we observed considerable and

consistent evidence that it falls into the same univer-

salityclassastheonsetofsuperﬂuidityin

He films in

disordered media, corrected for the long-rangeness

of the Coulomb interaction.The resulting criticalex-

ponents, z =1and

 ≈ 1, are also consistent with

the empirical relations ((11.2),(11.2) and (11.3)) and

the observed temperature and magnetic field depen-

dence of the specific heat coefficient in the limit of

zero temperature. These properties also point to a

3D–QSN transition with z =2and

 ≈ 1/2, describ-

ing a d-wave superconductor to disordered metal

transition at weak coupling. Here the disorder de-

stroys superconductivity, while at the 2D–QSI tran-

sition it localizes the pairs and destroys superﬂuidity.

Due to the existence of the 2D–QSI and 3D–QSN crit-

icalpoints,thedetectionof finitetemperature3D–XY

critical behavior will be hampered by the associated

crossovers that reduce the temperature regime where

thermal 3D–XY ﬂuctuations dominate. In any case,

our analysis clearly revealed that the universality of

the empirical correlations reﬂect the ﬂow to 2D–QSI

and 3D–QSN criticality.Moreover, the doping tuned

superconductivity in bulk cuprate superconductors

turned out to be a genuine 3D phenomenon, where

the interplay of anisotropy and superconductivity

destroys the latter in the 2D limit.

11.3.3 Evidence for Substitution Tuned Quantum

Phase Transitions

It has been well established, both experimentally

and theoretically,that in conventional superconduc-

tors (e.g., A15 compounds or the Chevrel phases)

the presence of magnetic impurities depresses the

superconducting transition temperature more effi-

ciently than does the introduction of nonmagnetic

ions [109], and this has been ascribed to the break-

ing of pairs by the magnetic impurities.To determine

whether the cuprates behave similarly with respect to

magnetic impurities, extensive studies involving the

substitutionforCu by other 3d metals have been per-

formed [18,19].A result common to all these studies

is that T

is depressed in the same manner, indepen-

dent of whether the substituent is magnetic or non-

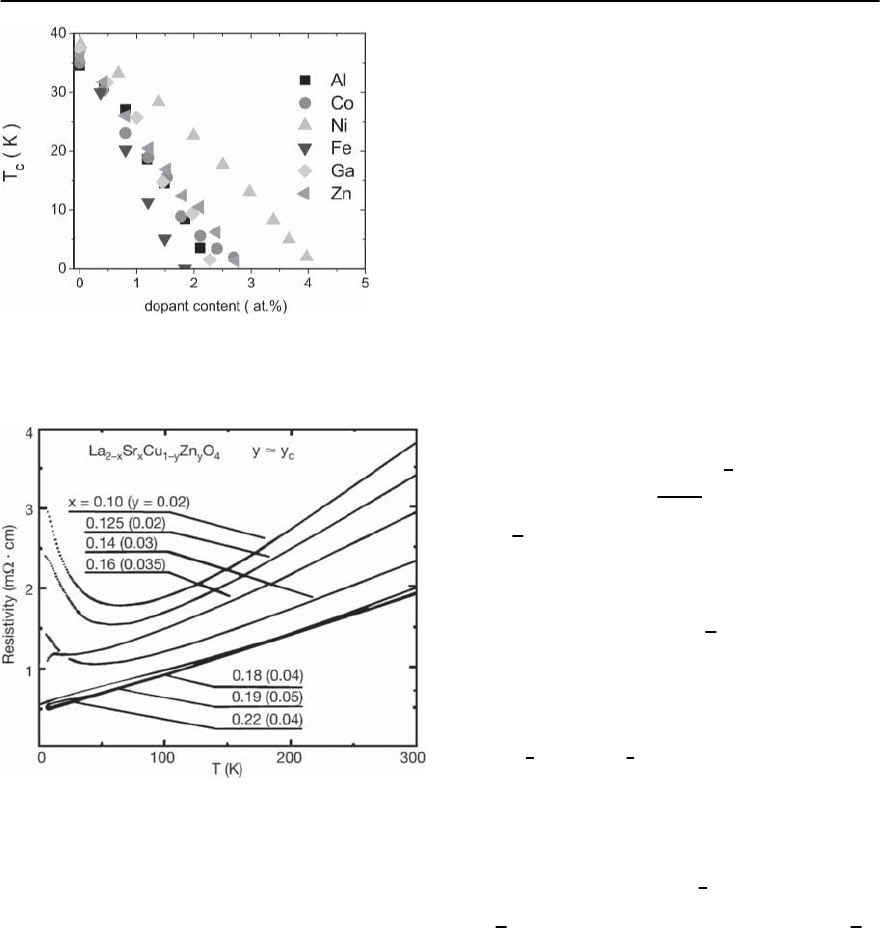
482 T. Schneider

Fig. 11.26. Variat ion of T

with substitution for

1.95

0.15

1−y

(A=Fe,Cu,Ni,Zn,GaandAl)(taken

from Xiao et al. [18])

Fig. 11.27. Temperature dependence of the resistivity for

2−x

1−y

at y

(

)

(taken from Momono et

al.[15])

magnetic, and in contrast to that observed in con-

ventional superconductors.

To illustrate this point in Fig. 11.26 we de-

picted the variation of T

with substitution for

1.95

0.15

1−y

(A=Fe, Cu, Ni, Zn, Ga and

Al) [18]. T

is seen to vanish at a critical substi-

tution concentration y

, where a quantum phase

transition occurs. The experimental data for

2−x

1−y

0.8

0.2

3−3y

7−ı

[110] and Bi

CaCu

2−2y

8+ı

[111] shows that

this behavior is not restricted to optimum doping.

Thus T

depends on both the dopant (x)andsub-

stitution concentration (y). Figure 11.3 shows the

resulting (T

, x, y) diagram for La

2−x

1−y

The blue curve, y

(

)

, is a line of quantum phase

transitions. At the corresponding critical endpoints

the system undergoes a 2D–QSI and 3D–QSN tran-

sition. Along the path marked by the green arrow,

a QSI and QSN transition is expected to occur. The

pink arrow indicates the crossover from insulating

to metallic behavior.

This scenario,emerging from the temperature de-

pendence of the resistivity of La

2−x

1−y

[15], is shown in Fig. 11.27. Along the phase tran-

sition line y

(

)

superconductivity disappears and

for x  0.16 metallic behavior sets in, while for

x  0.16 the resistivity exhibits insulating behavior

at low temperatures. For fixed x and close to y

(

)

scales according to (11.33) and (11.38) as





∝



1−

(

)



z

. (11.81)

Since z

 = 1 is expected to hold in both the doping

tuned 2D–QSI and 3D–QSN transition ((11.65) and

(11.67)), this combination should hold along the en-

tire line y

(

)

.Although the data shown in Fig. 11.26

is remarkably consistent with z

 = 1 it remains to be

understood why the linear relationship applies over

almost the entire substitution regime. Close to the

2D–QSI and 3D–QSN transitions,the singular part of

the free energy density scales in analogy to (11.36) as

∝ ı

 (D+z

)



yı

−



, ı = x/x

−1, 1−x/x

(11.82)

F is a scaling function of its argument.A phase tran-

sition is signaled by a singularity of the scaling func-

tion at some value of its argument. Thus,

(

)

∝ ı



, (11.83)

with

 = 1 close to the 2D–QSI (see (11.65)) and  =

1/2 near the 3D–QSN transition(see (11.67)).There-

sulting phase transitionline is shown in Fig.11.28for

2−x

1−y

, where we included the experi-

mental data for comparison. As expected from the

doping dependence of the correlation lengths (see

Fig. 11.20) close to the 3D–QSN transition y

(

)

ex-

hibits a very narrow critical regime. For this reason

the data considered here is insufficient to provide an

11 Universal Properties of Cuprate Superconductors 483

Fig. 11.28. y

versus x for La

2−x

1−y

. • :Taken

fromMomono etal.[15].Thesolid curve interpolates be-

tween the critical behavior of a 2D–QSI transition with

 =

1(dotted line: y

(

)

=0.03

(

x −5

)

)anda3D–QSNtran-

sition with

 =1/2(dashed line: y

(

)

=0.46

(

27 − x

)

1/2

)

estimate for  . Nevertheless,  =1/2yieldsareason-

able qualitative description of the quantum critical

line y

(

)

The picture we now have is summarized in the

phase diagram shown in Fig. 11.3. The blue curve

corresponds to the line of quantum phase transitions

(

)

shown in Fig. 11.28. Along this line, z

 =1is

expected to hold ((11.65) and (11.67)), while

 ≈ 1

(see (11.65)) at the 2D–QSI (y =0andx = x

)and

 =1/2atthe3D–QSN((y =0andx = x

) transi-

tion. According to the empirical correlation between

and anisotropy 

(see (11.3) and Fig. 11.2), the

initial value of the dopant concentration determines

whether the ﬂow upon substitution leads to 2D–

QSI or 3D–QSN criticality. For initially underdoped

cuprates, the rise of 

,tuned by the substitution in-

duced reduction of T

,drives the ﬂow to2D–QSI crit-

icality. Conversely, in initially overdoped cuprates,

the fall of 

to a finite value directs the ﬂow to 3D–

QSN criticality.The mechanism whereby the substi-

tution of Cu leads to a reduction of T

and finally

to the quantum critical line y

(

)

appears to be not

well understood. When the aforementioned univer-

sality classes of the 2D–QSI and 3D–QSN transitions

hold true ((11.65) and (11.67)), disorder plays an es-

sential role.At 2D–QSI criticalityit localizes the pairs

anddestroyssuperﬂuidity [52,53] andat the3D–QSN

transition it destroys superﬂuidity and the pairs [54].

In this context we also note that the phase diagram

of La

2−x

CuO

4+ı

shown in 11.4,revealsthat isotope

substitutionleads to identicalbehavior,although less

pronounced (taken from unpublished work of Guo-

Meng Zhao et al.. Since isotope substitution is ac-

companied by local lattice distortions, we conclude

that in addition to disorder, lattice degrees of free-

dom tune superconductivity in an essential man-

ner. Another essential facet emerges from the fact

that the doping and substitution tuned ﬂow to the

2D–QSI critical point is associated with an enhance-

ment of 

. Thus, despite the fact that the fraction

 =



1/

(

)





1/

(

)

+1/

(

)

+1/

(

)





1+2

T=0



[13], which the third dimension con-

tributes to the superﬂuid energy density in the

ground state, is very small, this implies that a finite

is inevitablyassociated with an anisotropicbut3D

condensation mechanism, because 

is finite when-

ever superconductivity occurs (see Fig. 11.2). This

points unambiguously to the conclusion that theo-

ries formulated fora single CuO

plane cannot be the

whole story. It does not imply, however, a 3D pairing

mechanism because in the presence of ﬂuctuations

pairing and superﬂuidity occur separately.

11.3.4 Evidence for Magnetic Field Tuned Quantum

Phase Transitions

We have seen (Sect. 11.2) that a strong magnetic field

destroys superconductivity at finite temperature. In

sufficiently clean systems this destruction occurs at

the first-order vortex melting transition. However,

in the presence of disorder, the long-range order of

the vortex lattice is destroyed and the vortex solid

becomes a glass [27]. The vortex ﬂuid to glass transi-

tion appears to be a second-order transition,signaled

by the vanishing of the zero-frequency resistance in

the vortex glass phase. Since disorder plays an es-

sential role at 2D–QSI and 3D–QSN criticality, one

expects a line H

(

)

of vortex glass to ﬂuid quan-

tum phase transitions,leading to the schematic phase

diagram depicted in Fig. 11.5. There is the supercon-

ducting phase (S), bounded by the zero-field transi-

tion line,T

(

x, H =0

)

,the criticallines of the vortex

melting or vortex glass to vortex ﬂuid transitions,

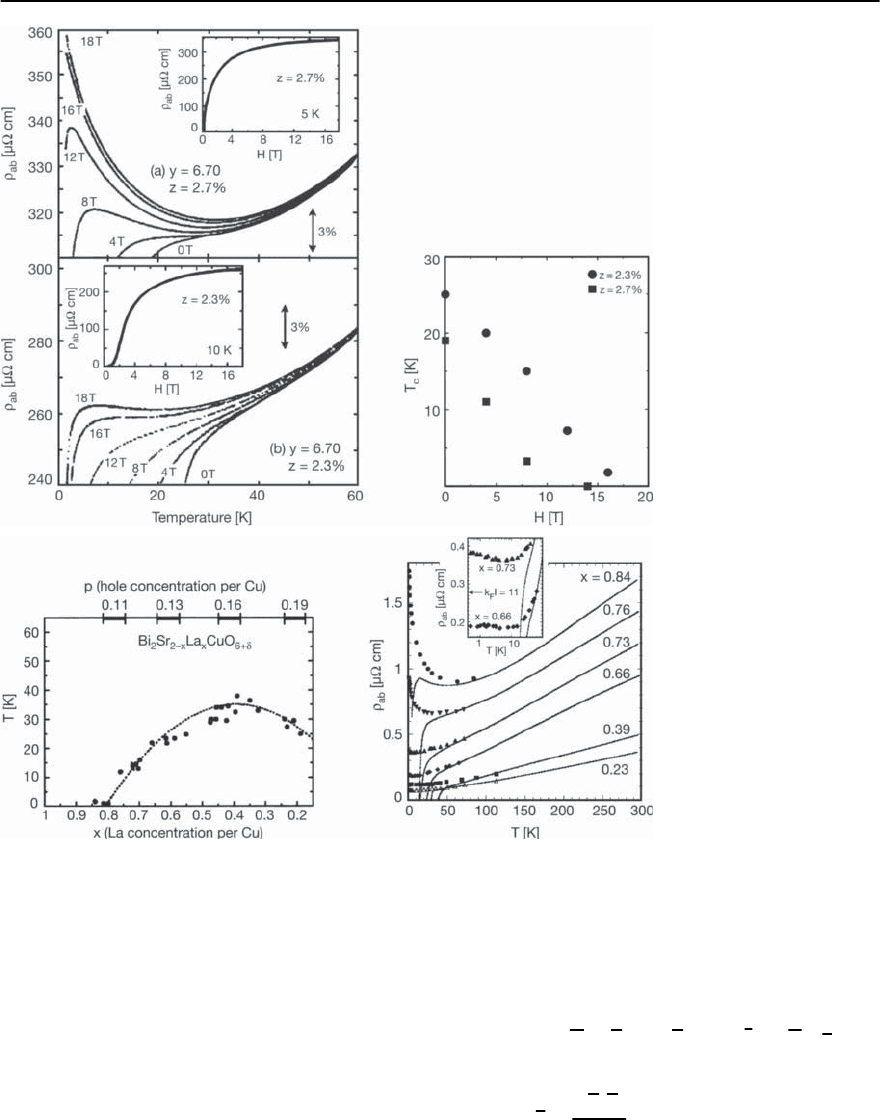
484 T. Schneider

Fig. 11.29. Left panel:In-

plane resistivity 

versus

T at H =0, 4, 8, 16 and

18 T for YBa

3−z

a: y =6.7, z =2.7%

and b: y =6.7, z =

2.3%. Taken from Segawa

et al. [30]. Right panel:

Schematic (H, T)-phase di-

agram of YBa

3−z

derived from the data

shownintheleft panel

Fig. 11.30. Left panel:PhasediagramofBi

2−x

CuO

6+ı

in the doping concentration (x or p)-temperature plane. Taken

from Ono et al. [31]. Right panel: Temperature dependence of 

for a Bi

2−x

CuO

6+ı

crystal in H =0and60Tfor

various dopant concentrations x.Theinset shows a clearer view of the low temperature behavior for x =0.66 and 0.73

(taken from Ono et al. [31])



x = fixed, H



and the line of quantum critical

points, H

(

x, T =0

)

. Along this line superconduc-

tivity is suppressed and the critical endpoints coin-

cide with the 2D–QSI and 3D–QSN critical points

at x

and x

, respectively. To fix the critical line

(

x, T =0

)

close to the 2D–QSI and 3D–QSN tran-

sitions, we note that the singular part of the ground

state energy density scales in analogy to (11.36) as

(

ı, T

)





−

,0

i=1



−

i,0

−1

 (D+z

)

(

)

z =



, (11.84)

11 Universal Properties of Cuprate Superconductors 485

where H corresponds to a field applied parallel to the

c-axis. Supposing that in the (H, ı)planethereisa

continuous transition first order melting transition.

Then the scaling function

(

)

will exhibita singu-

larity at some universal value

z = z

.Thusclosethe

2D–QSI and 3D–QSN critical endpoints the quantum

critical line (see Fig.11.5) is given by

(

)



a,0



b,0

2

, (11.85)

with

 ≈ 1 (see (11.65)) and  ≈ 1/2 (see (11.67))

close to 2D–QSI and 3D–QSN criticality,respectively.

Moreover, the singular behavior of the scaling func-

tion

(

)

must be such as to enable the correlation

length when H = 0 to correspond to the vortex glass

transition,so that



= 

H,0



H − H

(

)

(

)



−

. (11.86)



is the correlation length exponent of the vortex

glass to ﬂuid transition. Noting that T

∝ ı

 z

∝ 

−z

(see (11.34) and (11.38), with (11.86) we obtain for

the magnetic field induced reduction of T

the rela-

tion

(

)

∝

(

)

− H

)



. (11.87)

isthedynamic criticalexponentof the vortexglass

to ﬂuid transition.

The existence of a quantum phase transition line

(

)

can be anticipated from the in-plane re-

sistivity data for YBa

3−z

of Segawa et al.

[30] shown in the left panel of Fig. 11.29. With in-

creasing magnetic field strength T

is depressed.

In the sample with y =6.7andz =2.7% the

temperature dependence of 

clearly points to a

magnetic field tuned QSI transition around 16 <



y =6.7, z =2.7%



 18T.SinceH

(

)

scales as

2

∝

(

− z

)

2

(see (11.85)), H



y =6.7, z



should

increase with reduced Zn concentration z.Thisbe-

havior is consistent with the data for z =2.3%,where



y =6.7, z =2.3%



> 18T. The emerging (H, T)

phase diagram,consistingof finite temperature tran-

sition lines (vortex glass to ﬂuid transitions) with

2D–QSI critical endpoints is displayed in the right

panel of Fig. 11.29. In the schematic (x, H, T)-phase

diagram shown in Fig. 11.5, these lines result from

cuts near the zero field 2D–QSI transition with x re-

placed by z.

Related behavior was also observed in

2−x

CuO

[29] and Bi

2−x

CuO

6+ı

[31]. In

the hole doped La

2−x

CuO

[29] and the elec-

tron doped Pr

2−x

4+ı

a magnetic field tuned

metal to insulator crossover was observed close to

optimum doping, while in Bi

2−x

CuO

6+ı

[31]

the crossover sets in well inside the underdoped

regime. The phase diagram of Bi

2−x

CuO

6+ı

displayed in the left panel of Fig. 11.30. In the under-

doped limit (x ≈ 0.84) the transition temperature

vanishes and a 2D–QSI transition is expected to oc-

cur. Evidence for this transition emerges from the

temperature dependence of 

shownintheright

panel of Fig. 11.30 [31], taken at H =0and60T

for six doping levels x. To strengthen this point in

Fig. 11.31 we plotted the resulting T

versus 

0,c

− 

for x =0.76, 0.73 and 0.66 and 

0,c

≈ 0.5 m§cm

at H = 0. Apparently there is suggestive consis-

tency with the 2D–QSI scaling relation (11.42) with

 ≈ 1, as well as with the corresponding data for

2−x

CuO

and YBa

7−ı

shown in Fig. 11.15.

As the 60T data (symbols) are concerned, the sam-

ples closest to the QSI transition (x =0.76 and 0.84)

exhibit a pronounced upturn in 

at low temper-

atures.Thispointstoaninsulatingnormalstate.

Indeed, the weak upturn below 6 K at x =0.73, vis-

ible in the inset of Fig. 11.30, signals the proximity

to the onset of insulating behavior, while the low

T behavior of the x =0.66 sample with T

(

H =0

)

= 23 K exhibits metallic behavior. Thus, there is

a metal to insulator (MI) crossover. The emerging

(x, T, H)-phase diagram is displayed in Fig. 11.32.

The arrows mark the ﬂows emerging from the ex-

perimental data displayed in Fig. 11.30 for x =0.84

(1) and x =0.66 (2).

This differs from the behavior observed in

2−x

CuO

where the detectable MI-crossover ap-

pears to set in close to optimum doping.In Fig. 11.33

we depicted the logarithmic plot of 

(

)

for

2−x

CuO

6+ı

and La

2−x

CuO

crystals for

H = 0 and 60T and various doping concentrations

[31]. Concentrating on the presence or absence of an

upturn,it is clearly seen that in La

2−x

CuO

the MI-

486 T. Schneider

Fig. 11.32. Schematic (x, T, H)-phase diagram

close to the 2D–QSI transition. There is the su-

perconducting phase (S), bounded by the zero-

field transition line, T

(

x, H =0

)

,thelines

of the vortex melting or vortex glass to vor-

tex ﬂuid transitions T



x = fixed, H



and the

quantum critical line H

(

)

. The critical lines

(

x, H =0

)

and H

(

)

merge in the under-

doped limit (x = x

) where a doping driven

quantum superconductor to insulator (QSI)

transition (•)occurs.Thearrows mark the

ﬂows emerging from the experimental data

shown in Fig.11.31 at x =0.84 (1), x =0.66 (2)

Fig. 11.31. T

versus 

0,c

− 

for Bi

2−x

CuO

6+ı

.De-

duced from the data shown in Fig. 11.30 for x=0.76, 0.73

and 0.66 and 

0,c

=0.5m§ cm. The straight line is the

scaling relation (11.70) with z

 ≈ 1

crossover occurs around x ≈ 0.15, corresponding to

optimum doping. However,it should be kept in mind

that this crossover is nonuniversal. For this reason,

the dopant concentration where insulating behavior

is detectable is expected to be material-dependent.

The magneto resistance 

(

H, T

)

of underdoped

2−x

CuO

films with x ≈ 0.048

(

=0.45K

)

and 0.051

(

=4K

)

was also studied in mag-

netic fields up to 0.5 T and at temperatures down

to 30mK [112]. The temperature dependence of



(

H, T

)

of the film closest to the 2D–QSI tran-

Fig. 11.33. Logarithmic plot of 

(

)

for

2−x

CuO

6+ı

and La

2−x

CuO

crystals in H =0T

(solid lines)and60T(filled circles), labeled by La con-

centration, x.The straight line indicates consistency with

the log(1/T)behavioratx =0.84. and open circles are

H =30Tdata.La

2−x

CuO

data in H =0T(dashed

lines)andin60T(open squares),labeled by the Sr concen-

tration x (taken from Ono et al. [31])

11 Universal Properties of Cuprate Superconductors 487

sition

(

x ≈ 0.048, T

=0.45K

)

was found to be con-

sistent with 

∝ exp



(

T/T

)

1/3



below 1 K and for

fields from 4 to 6 T. Thus this study points to 2D-

localization. On the other hand, the data of Ando et

al. [28] (Fig. 11.33) appears to be consistent with a

logarithmic divergence of the normal-state resistiv-

ity down to 0.7K for x =0.08 and H = 60 T, suggest-

ing 2D weak localization. In any case, the evidence

for 2D localization confirms an essential property of

2D–QSI criticality: disorder localizes the pairs and

destroys superﬂuidity [52,53].

11.4 Thin Films

There is considerable evidence that the quantum su-

perconductor to insulatortransitionin thin films can

also be traversed by changing a parameter such as

film thickness, disorder, etc. [13]. As far as cuprates

are concerned, an instructive example are the mea-

surements of YBa

7−ı

slabs of thickness d sep-

arated by 16 unit cells (≈ 187 A) of PrBa

.Due

to the large separation the YBa

7−ı

slabs can

be considered to be essentially to be uncoupled. As

shown in Fig. 11.6 in YBa

7−ı

slabs of thick-

ness d the transition temperature was found to vary

according to (11.4). Together with the scaling rela-

tion (11.38) this points to a 2D–QSI transition with

 = 1, in agreement with our previous estimate

(see (11.65)). Since quantum ﬂuctuations alone are

not incompatible with superconductivity, this 2D–

QSI transition must be attributed to the combined

effect of disorder and quantum ﬂuctuations. Never-

theless, it is conceivable that in cleaner films super-

conductivity may also occur at and below this value

of d

, which is close to the estimate derived from the

bulk (see (11.69)).What is seen is then superconduc-

tivity in 2D and due to the reduced dimensionality

ﬂuctuations will be enhanced over the full range of

dopant concentrations.As it stands, in the bulk (see,

e.g. Fig. 11.2) and chemically doped films supercon-

ductivity disappearsin the2D-limit.Sincechemically

doped materials with different carrier densities also

have varying amounts of disorder, the third dimen-

sion is apparently needed to delocalize the carriers

and to mediate superﬂuidity.

11.5 Concluding Remarks and Comparison

with Other Layered Superconductors

Evidence for power laws and scaling should prop-

erly consist of data that cover several decades in the

parameters. The various power laws that we have ex-

hibited span at best one decade and the evidence for

data collapse exists only over a small range of the

variables. Consequently, though the overall picture

of the different types of data is highly suggestive,

it cannot really be said that it does more than in-

dicate consistency with the scaling expected near a

quantum critical point or a quantum critical line.

Nevertheless, the doping, substitution and magnetic

field induced suppression of T

clearly reveal the ex-

istence and the ﬂow to 2D–QSI and 3D–QSN quan-

tum phase transition points and lines (see Figs. 11.1,

11.2, 11.3 and 11.5). In principle, their universal crit-

ical properties represent essential constraints for the

microscopic theory and phenomenological models.

As it stands, the experimental data is fully consis-

tent with a single complex scalar order parameter,

a doping induced dimensional crossover, a doping,

substitution or magnetic field driven suppression of

superconductivity, due to the loss of phase coher-

ence. When the evidence for this scenario persists,

antiferromagnetic and charge ﬂuctuationsare irrele-

vant close to criticality. Moreover, given the evidence

for the ﬂow to 2D–QSI criticality, the associated 3D–

2D crossover,tunedby increasing anisotropy,implies

that a finite T

and superﬂuid density in the ground

state of bulk cuprates is unalterably linked to a fi-

nite anisotropy. This raises serious doubts that 2D

models are potential candidates to explain supercon-

ductivity in bulk cuprates. Thus, there is convinc-

ing evidence that the combined effect of disorder

and quantumﬂuctuationsplays an essential role and

even destroys superconductivity in the 2D limit of

chemically doped cuprates. Thus, as far as the na-

ture of the quantum phase transitions in chemically

doped cuprates is concerned, disorder is an essen-

tialingredient.Wehaveseenthatthe2D–QSItransi-

tion has a rather wide and experimentally accessible

critical region. For this reason we observed consid-

erable and consistent evidence that it falls into the

same universality class as the onset of superﬂuid-

488 T. Schneider

ity in

He films in disordered media, corrected for

the long-rangeness of the Coulomb interaction. The

resulting critical exponents, z =1and

 ≈ 1are

also consistent with the empirical relations ((11.2),

(11.2) and (11.3)) and the observed temperature and

magnetic field dependence of the specific heat coef-

ficient in the limit of zero temperature. These prop-

erties also point to a 3D–QSN transition with z =2

and

 ≈ 1/2, describing a d-wave superconductor to

disordered metal transition at weak coupling. Here

the disorder destroys superconductivity, while at the

2D–QSI transition it localizes the pairs and destroys

superﬂuidity.Due to the existence of the 2D–QSI and

3D–QSN critical points, the detection of finite tem-

perature 3D–XY critical behavior will be hampered

by the associated crossovers that reduce the tem-

perature regime where thermal 3D–XY ﬂuctuations

dominate. In any case, our analysis clearly revealed

that superconductivity in chemically doped cuprate

superconductors is a genuine 3D phenomenon and

that the interplay of disorder (anisotropy) and su-

perconductivity destroys the latter in the 2D limit.As

a consequence, the universality of the empirical cor-

relations reﬂects the ﬂow to 2D–QSI and 3D–QSN

criticality, tuned by chemical doping, substitution

and an applied magnetic field. A detailed account

of the ﬂow from 2D–QSI to 3D–QSN criticality is

a challenge for microscopic theories attempting to

solve the puzzle of superconductivity in these mate-

rials. Although the mechanism for superconductiv-

ity in cuprates is not yet clear, essential constraints

emerge from the existence of the quantum critical

endpoints and lines. However, much experimental

work remains to be done to fix the universality class

of the 2D–QSI and particularly of the 3D–QSN criti-

cal points unambiguously.

In conclusion we note that universal properties

emerging from thermal and quantum ﬂuctuations

are not restricted to cuprate superconductors. Po-

tential candidates are the highly anisotropic organic

Fig. 11.34. 

(

)

versus 

for a variety of superconductors. YBa

7−ı

(YBCO) [114–118], La

2−x

CuO

4+ı

(LSCO)

[116,119, 120], HgBa

CuO

4+ı

(Hg1201) [121], Tl

CuO

6+ı

(Tl2201) [122–124], Bi

CaCu

8+ı

(Bi2212) [125, 126],

2−x

CuO

4+ı

(NCCO) [127]. Blue points: underdoped (UD), green points: optimally doped (OpD) and red points:

overdoped (OD). Transition metal dichalcogenides [144,145]; (ET)

X compounds [135–143]; (TMTSF)

ClO

[128–134];

RuO

[146,147];MgB

[148–150]; Nb [151,152]; Pb [152]; Nb Josephson junctions [153]; ˛Mo

1−x

[154]. The dotted

line is (11.88) and the dashed lines (11.58). The red arrows indicate the ﬂow to 2D–QSI and for overdoped YBa

7−ı

to 3D–QSN criticality, respectively