Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.

11 Universal Properties of Cuprate Superconductors 469
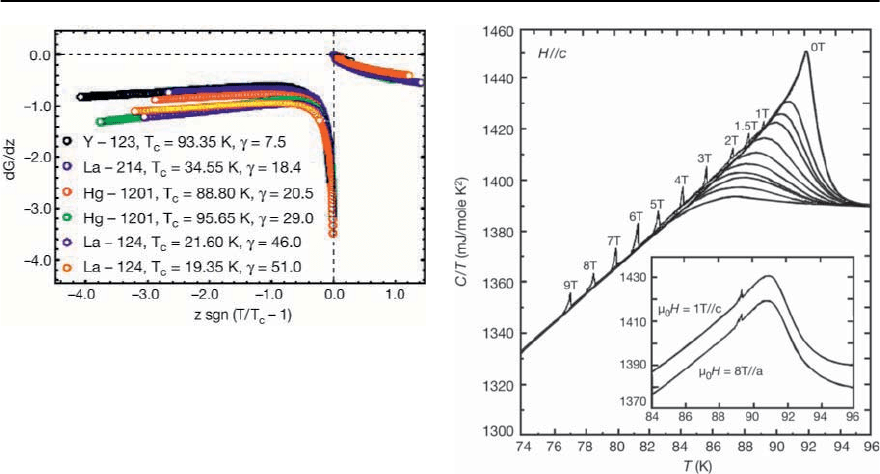
Fig. 11.9. Scaling function dG
±
3
(z)/dz derived from
the angular dependence of the magnetic torque
for YBa
2
Cu
3
O
6.93
,La
1.854
Sr
0.146
CuO
4
,HgBa
2
CuO
4.108
,
HgBa
2
CuO
4.096
,La
1.914
Sr
0.086
CuO
4
and La
1.920
Sr
0.080
CuO
4
(taken from [7])
tative behavior is the same for all samples, the de-
viations increase with rising
T
c
.Thissystematics
cannot be attributed to the experimental uncertain-
ties of about 40%. It is more likely that it reflects
the reduction of the temperature regime where 3D-
fluctuation dominates so that corrections to scaling
become important [13].With this view,it is clear that
due its moderate anisotropy [13,38],optimally doped
YBa
2
Cu
3
O
7−ı
isparticularly suitedfor observing and
checking the consistency with 3D–XY-criticalbehav-
ior.In contrast to this, in highly anisotropic cuprates
like Bi
2
Sr
2
CaCu
2
O
8−ı
, it will be difficult to enter the
regime where 3D fluctuations dominate [69]. Nev-
ertheless, since the critical behavior of the charged
fixed point is the only alternative left, it becomes
clear that even the intermediate critical behavior
of highly anisotropic cuprates like Bi
2
Sr
2
CaCu
2
O
8−ı
falls into the 3D–XY universality class. Fluctuations
grow with increasing , they become essentially 2D
slightly away from T
c
..
The melting transition of the vortex lattice was
discovered in 1993in Bi
2.15
Sr
1.85
CaCu
2
O
8−ı
using the
SR technique [70]. An anomaly attributed to this
transition was observed in specific heat measure-
ments of YBa
2
Cu
3
O
7−ı
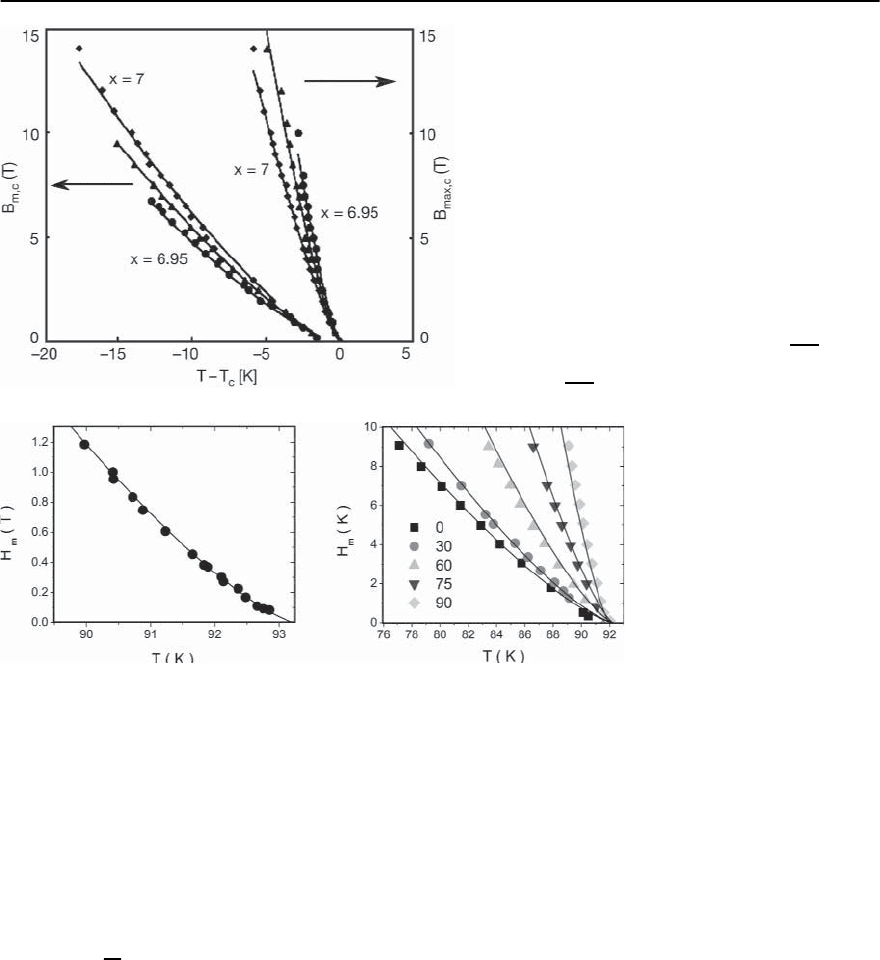
[71].InFig.11.10 we depicted
the temperature dependence of the specific heat co-
efficient of an untwined YBa
2
Cu
3
O
7−ı
single crystal
for various applied fields Hc.Ofparticularinter-
Fig. 11.10. Temperature dependence of the specific heat
coefficient for various applied magnetic fields
(
Hc
)
of
an untwined YBa
2
Cu
3
O
7−ı
single crystal. The numbers on
the top of the peak like features denote the applied field
strength. The inset shows representative data for H =1T
(
Hc
)
and H =8T
(
H(a, b)
)
, data shifted vertically by 10
mJ/molK
2
(taken from [71])
est in this context is the small anomaly below the
main peak, marked by the strength of the applied
field.It is attributed to the vortex melting transition.
Evidence for the first order nature of the transition
stems from magnetization measurements, revealing
ajumpatH
m
[72], which signals the singularity in
the scaling function G
±
3
(z)atz = z
m
(see (11.26)).
Due to the first order nature of the transition, the
correlation lengths remain bounded,so thatthe melt-
ing lineH
cm
and the temperature T
P
,wherethebroad
peak in the specific heat coefficient adopts its max-
imum value, should scale according to (11.30) and
(11.31). A glance at Fig. 11.11 shows that this behav-
ior is experimentally well confirmed. Note that the
variation of the amplitudes A
cm
and A
cp
is due to
the doping dependence of
a,0
b,0
( see (11.30) and
(11.31)).From(11.29) it can be seen that the melting
line also yields useful information on the anisotropy.
As an example we consider the angular dependence
in the (c, a) plane. Equation (11.29) yields
470 T. Schneider
Fig. 11.11. Melting line H
c,m
and H
c,max
versus T − T
c
for
aYBa
2
CuO
7−ı
single crystal with ı =0(), ı =0.03
()andı =0.053 (•)forHc. Taken from [73].
The curves correspond to H
cm
= A
cm
T
c
−T
T
c
2
and
H
cp
= A
cp
T
c
−T
T
c
2
with =2/3
Fig. 11.12. Left panel: Melting line for YBa
2
Cu
3
O
7−ı
with T
c
=93.25 K derived from field
(
'
)
and angular-dependent
(
)
torque curves. The solid line corresponds to H
m
∝
(
1−T/T
c
)
2
with =2/3. Data taken from [74].Right panel:Melting
lines H
m
(
ı, T
)
for YBa
2
Cu
3
O
7−ı
with T
c
= 92 K, detected by a direct measurement of the entropy change. The symbols
denote experimental data taken at different magnetic field orientations in the (c, a)plane,measuredbytheangleı [75].
The solid lines are (11.33) with
ca
=7.6and =2/3
H
m
(
ı
)
= H
m
(
ı =0
)
ca
(11.32)
×
sin
2
(
ı
)
+
2
ca
cos
2
(
ı
)
−1/2
,
where
ca
=
a
c
, H
m
(
ı =0
)
∝
(
1−T/T
c
)
2
.
From Fig. 11.12 it can be seen that this behavior is
well confirmed. In this context the question arises as
to whether or not phase coherence and with that su-
perfluidity persists above the melting line. Recently,
numerical simulations revealed that the vortex liq-
uid is incoherent, i.e. phase coherence is destroyed
in all directions, including the direction of the ap-
plied magnetic field, as soon as the vortex lattice
melts [76,77].
To summarize, there is considerable evidence that
the intermediate finitetemperature criticalbehavior
of cuprate superconductors, when attained, is equiv-
alent to that of superfluid helium. Moreover, we have
seen that finite size scaling is a powerful tool to iden-
tify and characterize inhomogeneities.
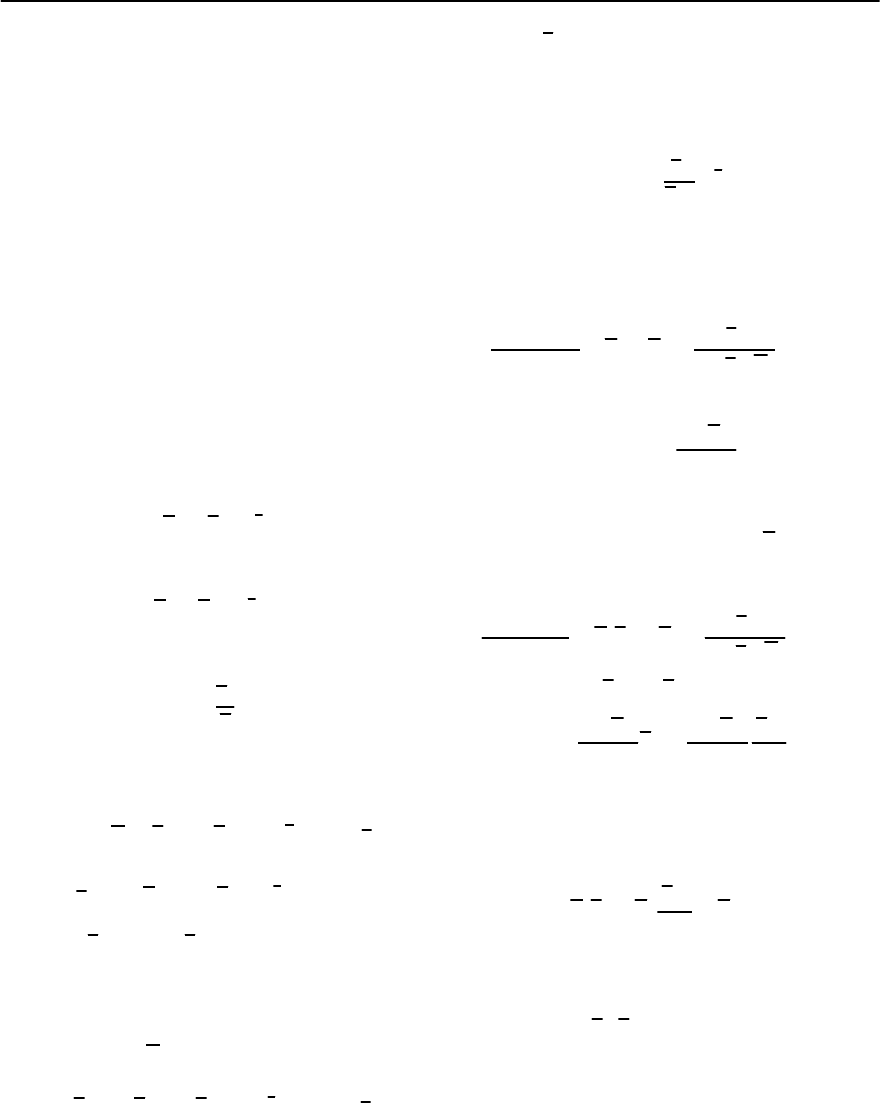
11 Universal Properties of Cuprate Superconductors 471
11.3 Quantum Critical Behavior and
Crossover Phenomena
11.3.1 Sketch of the Scaling Predictions
Given the empirical phase transition line T
c
(
x
)
or
surface T
c
x, y
with critical endpoints or lines (see
Figs. 11.1 and 11.3) doping and substitution tuned
quantum phase transitions can be expected. To in-
voke and sketch the scaling theory of quantum crit-
ical phenomena we define ı, measuring the relative
distance from quantum critical points, in terms of
ı =
⎧
⎨
⎩
y =0 :ı =
(
x − x
u
)
/x
u
y =0 :ı =
(
x
o
− x
)
/x
o
y =0, x
u
≤ x ≤ x
o
: ı =
y
c
(
x
)
− y
/y
c
(
x
)
.
(11.33)
At T = 0 and close to quantum criticality one has
two kinds of correlation lengths [13,40]. The usual
spatial correlation length in direction i
−
i
=
−
i,0
ı
−
(11.34)
and the temporal one
−
=
−
,0
ı
−
,
where the dynamic critical exponent is defined as the
ratio
z =
. (11.35)
The singular part of the free energy density then
adopts the scaling form [13,14,40]
f
s
(
ı, T
)
=
Q
D
−
,0
D
A
i=1
−
i,0
%
−1
ı
(
D+z
)
F
D
y
,
y = k
B
T
= k
B
T
,0
ı
−z
, (11.36)
where F
D
y
with F
D
y =0
= 1 is a universal scal-
ing function and Q
D
a universal constant. Another
quantity of interest is the helicity modulus, which
adopts the scaling form [13,14]
¤
D
i
(
ı, T
)
=
Q
D
(11.37)
×
−
i,0
2
−
,0
D
A
i=1
−
i,0
%
−1
ı
(
D−2+z
)
Y
D
y
,
where Y
D
y
with Y
D
y =0
= 1 is a universal scal-
ing function of its argument. As a first application
we consider a line of finite temperature transitions
T
c
(
ı
)
ending at a quantum critical point at T =0
and ı = 0. The scaling forms then require that
k
B
T
c
=
y
c
−
,0
ı
z
, (11.38)
where y
c
is the universal valueof the scaling function
argument at which the scaling functions exhibit a
singularity at finite temperature. Combining (11.38)
and (11.38) we obtain in D =2
k
B
T
c
¤
D=2
ab
(
ı, 0
)
=
R
2
, R
2
=
y
c
Y
2
y
c
Q
2
, (11.39)
yielding the universal relation
T
c
2
ab
(
0
)
=
¥
2
0
R
2
16
3
k
B
d
s
(11.40)
between transition temperature and zero tempera-
ture in-planepenetration depth.d
s
denotesthe thick-
ness of the superconducting slab and
R
2
is a univer-
sal dimensionless constant. Analogously, in D =3,
(11.38) and (11.38) yield
k
B
T
c
¤
D=3
ab
(
ı, 0
)
=
R
3
−
c
, R
3
=
y
c
Y
3
y
c
Q
3
, (11.41)
so that T
c
,
2
ab
(
0
)
,
−
c
and
−
ab
are related by
T
c
2
ab
(
0
)
=
¥
2
0
R
3
16
3
k
B
−
c
=
¥
2
0
R
3
16
3
k
B
−
ab
T=0
. (11.42)
This is just the quantum analogy of the universal fi-
nite temperature relation (11.23). When there is an
anisotropy tuned 3D–2D crossover, where
T=0
→
∞, matching of (11.40) and (11.42) requires that
R
3
−
c
= R
3
−
ab
T=0
= R
2
d
s
. (11.43)
Noting then that theuniversal relation(11.42) applies
close to both,the 2D–QSI and 3D–QSN transitions it
is expected to provide useful informationon the cor-
relation lengths (
−
c
,
−
ab
),given experimental data for
T
c
2
ab
(
0
)
and
T=0
.
Moreover, useful scaling relations for the specific
heat coefficient
c
are readily derived from the sin-
gular part of the free energy density (11.36), namely:
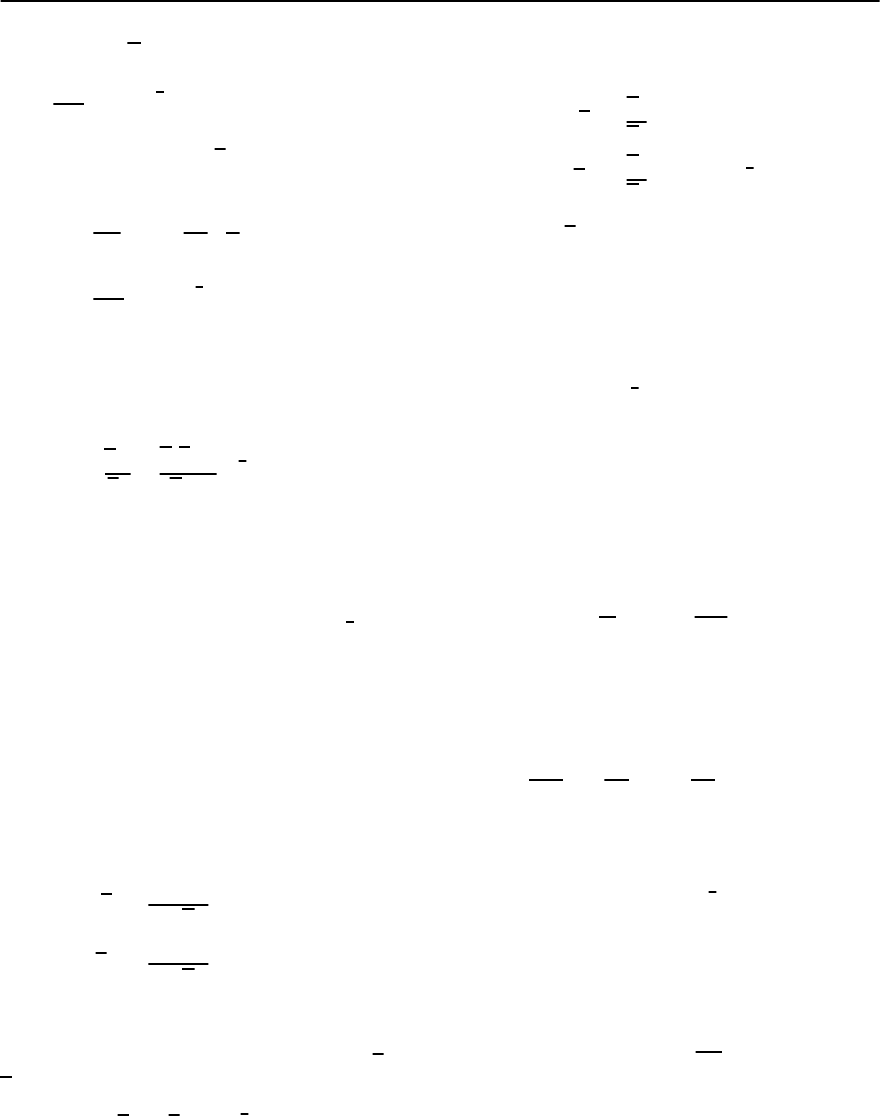
472 T. Schneider
c
T=0
=
c
T
T=0
= (11.44)
@
2
f
s
@T
2
T=0
∝ ı
(D−z
)
∝ T
(
D−z
)
/z
c
∝ H
(
D−z
)
/2
c
,
since H
c
scales as H
c
∝
−
ab
−2
[13], when applied
parallel to the c-axis, and
d
c
dT
T=0
=
d
dT
c
T
T=0
= (11.45)
@
3
f
s
@T
3
T=0
∝ ı
(D−2z
)
∝ T
(
D−2z
)
/z
c
.
Finally, considering 2D quantum critical points re-
sulting from a 3D–2D crossover in the ground state,
(11.43) implies that close to 2D quantum criticality
the anisotropy diverges as
T=0
=
−
ab
−
c
=
R
3
−
ab,0
R
2
d
s
ı
−
∝ T
−1/z
c
. (11.46)
Combining the scaling relations (11.38), (11.40),
(11.43) and (11.46) a 2D quantum critical point re-
sulting from a 3D–2D crossover is then characterized
by
T
c
∝
−2
ab
(
0
)
∝ n
s
(
0
)
∝
−z
T=0
∝ ı
z
,
c
T=0
∝ T
(
2−z
)
/z
c
∝ H
(
2−z
)
/2
c
. (11.47)
n
s
(
0
)
=
d
s
/
2
ab
(0)
denotes aerial superfluid den-
sity. In particular it relates the superconducting
properties to the anisotropy parameter, fixing the
dimensionality of the system. It reveals that an
anisotropy driven 3D–2D crossover destroys super-
conductivity even in the ground state.
From (11.42), rewritten in the form
−
c
=
16
3
k
B
¥
2
0
R
3
T
c
2
ab
(
0
)
,
−
ab
=
16
3
k
B
¥
2
0
R
3
T
c
2
ab
(
0
)
T=0
, (11.48)
it can be seen that T
c
2
ab
(
0
)
and T
c
2
ab
(
0
)
T=0
are ap-
propriate indicators for the occurrence of quantum
phasetransitions.Closeto 3D–QSNcriticality
−
c
and
−
ab
diverge according (11.34) as
3D-QSN:
−
c
∝
−
ab
∝ ı
−
∝ T
−1/z
c
, (11.49)
because
T=0
remains finite.This differs from the2D–
QSI transition, where according to (11.46)
2D-QSI:
−
c
=
R
2
R
3
d
s
, (11.50)
−
ab
=
R
2
R
3
d
s
T=0
∝ ı
−
∝ T
−1/z
c
applies. Here
−
c
tends to a finite value, proportional
to the thickness d
s
of the sheets.
Another quantity of interest is the zero temper-
ature condensation energy. Close to 2D–QSI and
3D–QSN criticality it scales according to (11.36) and
(11.38) as
−E
(
T =0
)
∝ ı
(
D+z
)
∝ T
(
D+z
)
/z
c
. (11.51)
As expected, when superconductivitydisappears,the
condensation energy vanishes.
Next we turn to the critical behavior of the con-
ductivity. In the normal state and close to a 3D–XY
critical point, the DC conductivities, parallel (
DC
ab
)
and perpendicular (
DC
c
) to the layers, scale as [13]
DC
ab
∝
c
,
DC
c
∝
c
2
ab
, (11.52)
where
is the correlation length associated with the
finite temperature critical dynamics. At T
c
the ratio
is then simply given by the anisotropy
DC
c
DC
ab
=
c
ab
2
=
1
T
c
2
. (11.53)
Approaching 2D–QSI criticality, the scaling relation
(11.47) implies
T
c
=
T
c
,0
ı
−
. (11.54)
Another essential property of this critical point is
that for any finite T
c
the in-plane areal conductivity
is always larger than [13,40]
DC
ab
d
s
=
0
4e
2
h
. (11.55)
This follows from the fact that close to 2D–QSI the
in-plane resistivity adopts the scaling form [13,40]
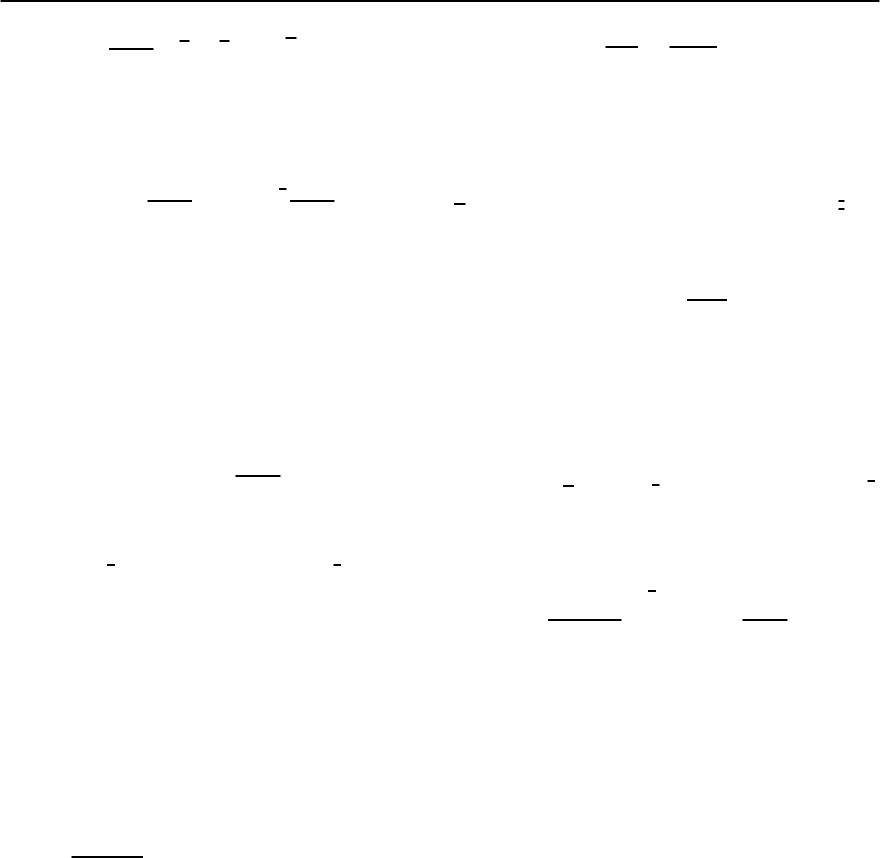
11 Universal Properties of Cuprate Superconductors 473
ab
=
h
4e
2
0
F
y
, y = k
B
T
. (11.56)
Thus, close to a 2D–QSI transition the normal state
resistivity
DC
c
T
+
c
=1/
DC
c
T
+
c
,evaluatedclose
but slightly above T
c
, is predicted to diverge as
DC
c
T
+
c
=
2
T
c
h
4e
2
0
=
2
T
c
,0
ı
−2
h
4e
2
0
. (11.57)
F
y
is a scaling functionof itsargument and F
(
0
)
=
1. This behavior uncovers the 3D–2D crossover asso-
ciated with the flow to 2D–QSI criticality in the nor-
mal state. To establish a relation between normal and
superconducting properties,we express ı in terms of
c
(
0
)
. Using (11.47) we obtain
c
(
0
)
= §
s
DC
c
T
+
c
−
(
2+z
)
/4
,
§
s
=
0,0
ab,0
(
0
)
4e
2
0
h
2
T
c
,0
%
(2+z
)
/4
, (11.58)
where
T
=
T,0
ı
−
,
ab,0
(
0
)
=
ab,0
(
0
)
ı
−z /2
(11.59)
are the zero temperature critical amplitudes. The
scaling relation (11.58) differs from the mean-field
prediction for bulk superconductors in the dirty limit
[78] and layered BCS superconductors, treated as a
weakly coupled Josephson junction[79–81]:
c
(
0
)
= §
s
DC
c
T
+
c
−1/2
, (11.60)
where
§
s
=
c
2
4
2
(
0
)
1/2
,
(
0
)
=1.76k
B
T
c
, (11.61)
and
(
0
)
denotes the zero temperature energy gap.
Approaching 3D–QSN criticality, the finite tem-
perature relations (11.52) and (11.53) still apply, but
both
DC
c
and
DC
ab
diverge at T
c
,whiletheanisotropy
T
c
remains finite. For this reason
,thecorrelation
length associated with the finite temperature critical
dynamics, cannot be eliminated. Nevertheless, since
scales as,
∝
z
cl
ab
,wherez
cl
is the critical exponent
of the finite temperature dynamics, from (11.52) we
obtain the relation
DC
c
∝
c
2
ab
∝
T
c
ab
∝
z
cl
−1
ab
∝
z
cl
−1
ab,0
|t|
−
(
z
cl
−1
)
, (11.62)
valid close to 3D–XY critical points. Since close to
a 3D–QSN criticality, the doping dependence of the
finite temperature critical amplitude
ab,0
is given by
ab
(see (11.23) and (11.42)), with
c
(
0
)
∝ ı
−
2
(
1+z
)
((11.38)) we finally obtain the relationship between
c
(
0
)
and
c
T
+
c
the relationship
c
(
0
)
∝
c
T
+
c
1+z
2
(
z
cl
−1
)
, (11.63)
characterizing the flow to a 3D–QSN critical point in
the
c
(
0
)
,
c
T
+
c
plane.
Noting that the in-plane resistivity tends close to
2D–QSI criticality to a fixed value (see (11.56)),
ab
can also be used as a parameter measuring the dis-
tance from the critical point. This is achieved by set-
ting y = k
B
T
∝ Tı
−z
∝ T
0
ab
−
ab
/
0
ab
−z
.
Given then a transition line T
c
(
ı
)
ending at the 2D–
QSN critical point the scaling form (11.56) requires
that
T
c
∝
0
ab
−
ab
0
ab
z
,
0
ab
=
h
4e
2
0
(11.64)
because the scaling function F
y
exhibits a singu-
larity aty
c
,signaling thefinite temperature transition
line.
11.3.2 Evidence for Doping Tuned Quantum Phase
Transitions
The empirical correlations between T
c
, dopant con-
centration x and anisotropy
T
(see (11.2)–(11.3))
clearly point to the existence of quantum critical
endpoints. A glance at Fig. 11.2 shows that when T
c
vanishes in the underdoped limit the anisotropy
T
tends to infinity. Accordingly a 2D–QSI transition is
expected to occur. In the overdoped limit, T
c
van-
ishes again but the finite anisotropy implies a 3D–
QSN transition. Since the aforementioned empirical
correlationsturned out to be remarkably generic (see
Fig. 11.2) they appear to reflect universal properties
characterizing these quantum phase transitions. In-
deed, the empirical correlation (11.2) points with the
474 T. Schneider
Fig. 11.13. T
c
versus
ab
(T =0)
−2
for La
2−x
Sr
x
CuO
4
(': [84], :[9],: [83]) YBa
2
Cu
3
O
7−ı
((: [85]) and
Y
1−x
Pr
x
Ba
2
Cu
3
O
6.97
(⊗: [86]). The dashed and solid
lines correspond to (11.68)
scaling law (11.38) to z = 1 in both transitions.
Moreover, the empirical relation between T
c
and
T
(11.3), according to the scaling law (11.46) implies a
2D–QSI transition with
= 1. Thus, the universal-
ity classes emerging from the empirical relations are
characterized by the critical exponents:
2D-QSI: z =1,
=1, (11.65)
3D-QSN: z
=1. (11.66)
These 2D–QSI exponents are consistent with the the-
oretical prediction for a 2D disordered bosonic sys-
tem with long-range Coulomb interaction. Here the
loss of superfluidity is due to the localization of the
pairs, which is ultimately responsible for the transi-
tion [52,53]. A potential candidate for the 3D–QSN
transition is the Ginzburg–Landau theory proposed
by Herbut [54]. It describes a disordered d-wave su-
perconductor to metal transition at weak coupling
and is characterized by the critical exponents z =2
and
=1/2, except in an exponentially narrow re-
gion. Since the resulting z
coincides with the value
implied by the empirical correlation (11.2), with the
estimate (11.66) one expects,
3D-QSN: z =2,
=1/2 . (11.67)
A characteristic property of a 2D–QSI transition,
irrespective of the value of z
, is the universal re-
lation (11.40) between transition temperature and
zero temperature penetration depth. An instructive
example is the onset of superfluidity in
4
He films
adsorbed on disordered substrates, where the lin-
ear relationship between T
c
and aerial superfluid
density n
s
(
0
)
∝ d
s
/
2
ab
(
0
)
is well confirmed [82].
In cuprates, a nearly linear relationship between T
c
and
ab
(
T =0
)
−2
was established some time ago
by Uemura et al. [83]. In the present context, it is
not strictly universal, because d
s
,thethicknessof
the independent slabs, is known to adopt family-
dependent values [13, 87]. This fact can be antici-
pated from Fig. 11.13,showingexperimental data for
T
c
versus 1/
2
ab
(
T =0
)
of La
2−x
Sr
x
CuO
4
[9,83, 84],
YBa
2
Cu
3
O
7−ı
[85] andY
1−x
Pr
x
Ba
2
Cu
3
O
6.97
[86].With
T
c
in K and
ab
(T = 0) in A, the dashed and solid
straight lines correspond to
T
c
≈
3.210
8
2
ab
(
T =0
)
,
2.510
8
2
ab
(
T =0
)
. (11.68)
Invoking then the universal relation (11.40) we ob-
tain the estimate,
d
s
(
YBa
2
Cu
3
O
7−ı
)
d
s
(
La
2−x
Sr
x
CuO
4
)
≈
3.2
2.5
≈ 1.3 , (11.69)
which is consistent with d
s
(
YBa
2
Cu
3
O
7−ı
)
/
d
s
(
La
2−x
Sr
x
CuO
4
)
≈ 10.1 A/7.6 A ≈ 1.33, derived
from the thickness tuned QSI transition and the
crossing point phenomenon, respectively [13, 87].
Consequently, dT
c
/d(1/
2
(T = 0)) is not strictly
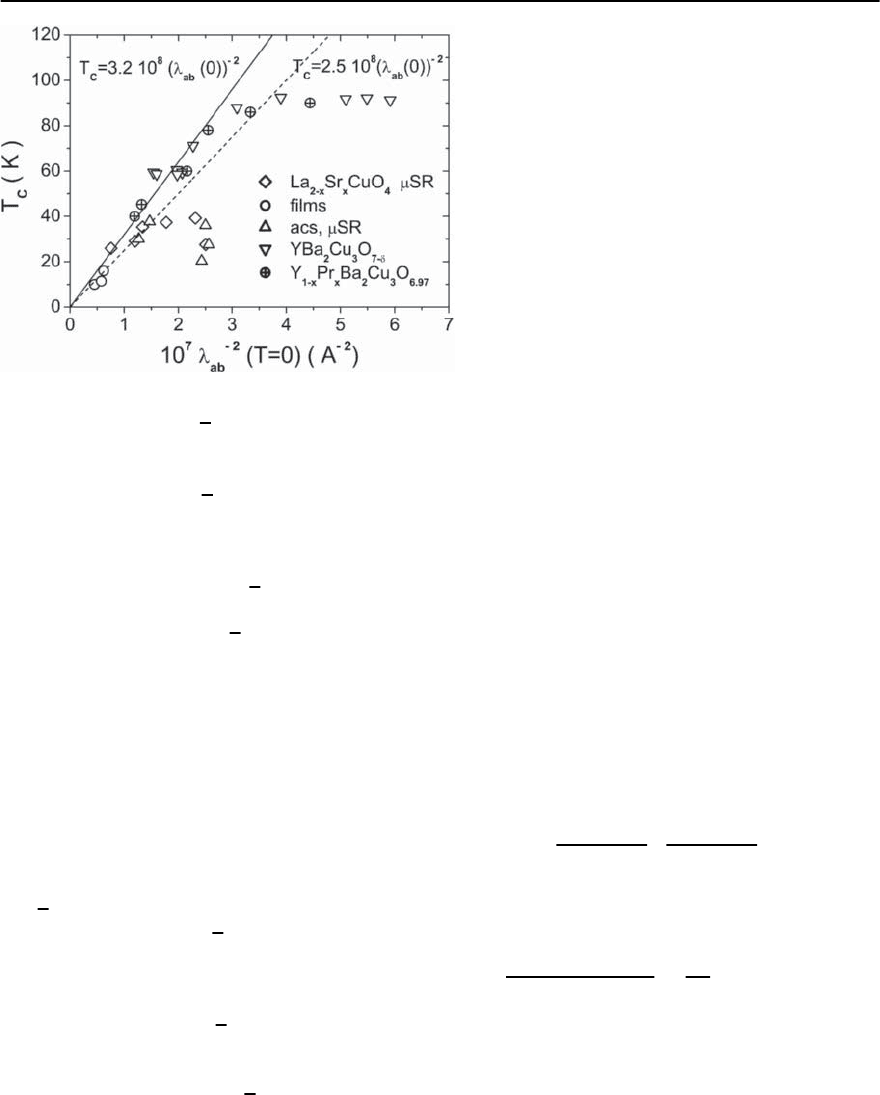
11 Universal Properties of Cuprate Superconductors 475
Fig. 11.14. Upper panel: Temperature dependence of the in-
plane resistivity
ab
of YBa
2
Cu
3
O
y
at various dopant con-
centrations y.TakenfromSembaandMatsuda[88].The
threshold resistivity is indicated by an arrow. Above panel:
c
/
ab
versus T of underdoped YBa
2
Cu
3
O
y
(taken from
Semba and Matsuda [88])
universal. Nevertheless, due to the small variations
of d
s
within a family of cuprates it adopts there a
nearly unique value. For this reason the empirical
proportionality of T
c
and
ab
(
T =0
)
−2
for under-
doped members of a given family confirms the flow
to 2D–QSI criticality.
Next we turn to the behavior of theresistivity close
to 2D–QSI criticality. In Fig. 11.14 we displayed the
data of Semba and Matsuda [88] for the tempera-
ture dependence of the in-plane resistivity
ab
of
YBa
2
Cu
3
O
y
at various dopant concentrations y.Be-
low y ≈ 6.3 the resistivity increases with decreasing
temperature,signaling the onset of insulating behav-
ior in the zero temperature limit. Above y ≈ 6.3
and as the temperature is reduced, the resistivity
drops rapidly and vanishes at and below T
c
.Thus,for
y 6.3 there is a superconducting phase andthe 2D–
QSI transition occurs at y ≈ 6.3. Moreover, the tem-
perature dependence of
c
/
ab
,depicted in Fig.11.14,
is in accord with the scaling relations (11.38) and
(11.53), yielding
c
/
ab
=
2
T
c
∝ ı
−2
∝ T
2/z
c
.In-
deed, the anisotropy increases by approaching the
2D–QSI transition. In contrast, near the 2D–QSI
transition (y ≈ 6.3), there is a finite threshold in-
plane resistivity
th
ab
≈ 0.8m§cm (see Fig. 11.14).
According to the scaling relation (11.55) this is a
characteristic feature of a 2D–QSI transitions. For
d
s
≈ 11.8A and
0
≈ 1 this leads to the sheet resis-
tance
th
ab
/d
s
≈ h/
4e
2
≈ 6.5 k§. Since
c
∝
2
ab
and
th
ab
→ d
s
h/
4e
2
it also becomes evident that
theriseof
c
forT > T
c
simply reflects the increasing
anisotropy and with that the flow to 2D–QSI critical-
ity. Together with the doping dependence of
Tc
(see
Figs.11.1and 11.2),these features clearly confirmthe
occurrence of a 2D–QSI transition.
According to (11.40) and (11.64)a 2D–QSI transi-
tion is also characterized by the scaling relation
k
B
T
c
= c
0c
−
0
0c
z
=
¥
2
0
16
3
Q
2
d
s
2
ab
(T =0)
,
(11.70)
where
0
and
0c
denote the residual and critical
residual sheet resistivity, respectively. This predic-
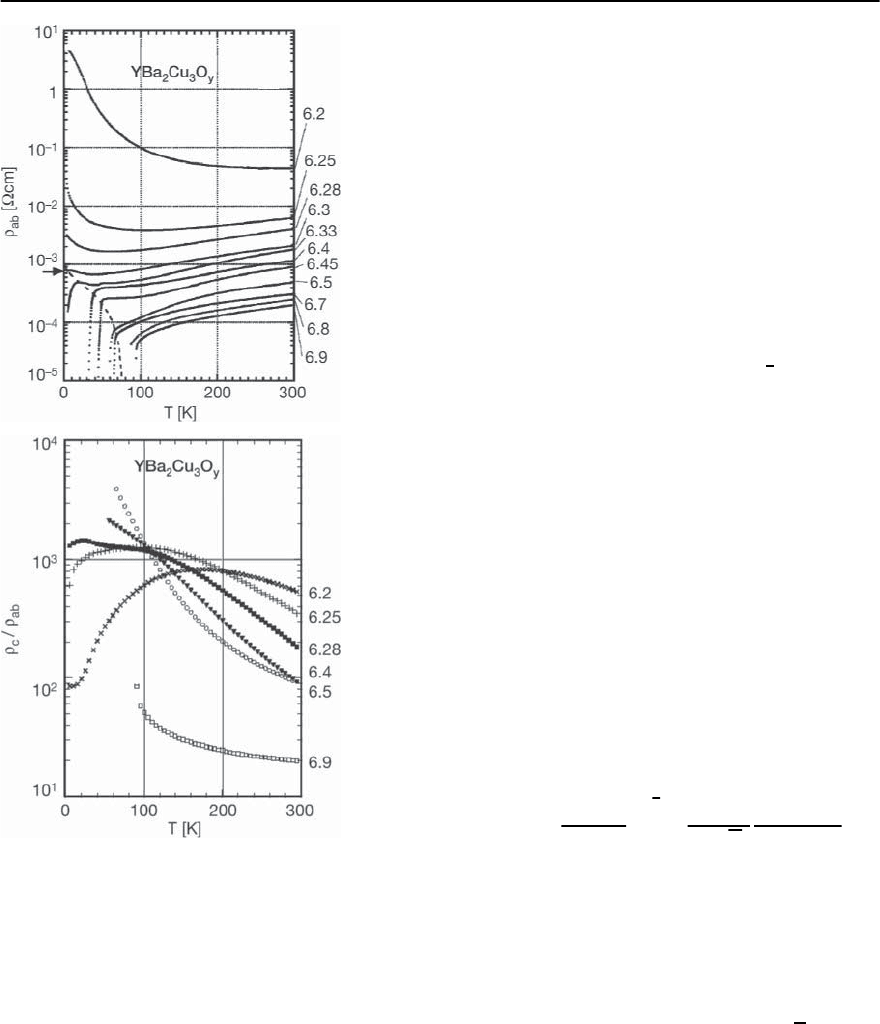
tion is well confirmed by the data of Fukuzumi et al.
for Zn-substituted La
2−x
Sr
x
CuO
4
and YBa
2
Cu
3
O
7−ı
[3] displayed in Fig. 11.15. Approaching the under-
doped limit the data merge on a straight line. With
the scaling relation (11.70) this points to z
= 1 con-
sistent with the value emerging from the empirical
correlations (Eq. (11.65)).
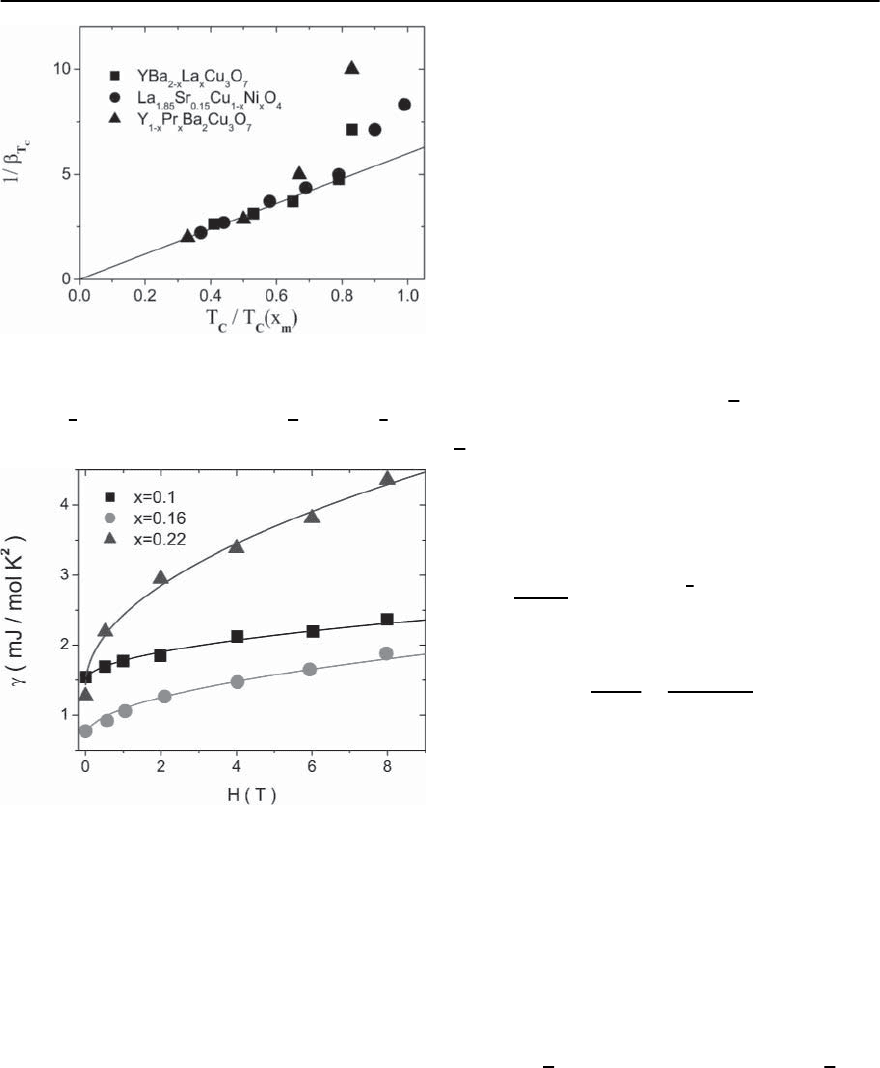
Next we turn to the isotope effect. Since universal
relations like (11.18), (11.23) and (11.40) should ap-
476 T. Schneider
Fig. 11.15. Residual in-plane resistance versus normalized
critical temperature for Zn-substituted La
2−x
Sr
x
CuO
4
and
YBa
2
Cu
3
O
7−ı
. T
c0
is the transition temperature of the Zn
free compound (taken from Fukuzumi et al. [3])
Fig. 11.16. Oxygen isotope effect for underdoped
La
2−x
Sr
x
CuO
4
in terms of 1/ˇ
1/
2
ab
(
0
)
versus 1/ ˇ
T
c
.The
dashed line marks the critical behavior at the 2D–QSI
transition (ˇ
1/
2
ab
(
0
)
→ ˇ
T
c
→∞), while the solid curve
is (11.71) with ˇ
d
s
=−0.2. Experimental data taken from
• [89], [90] and [91]
ply irrespective of the doping and substitution level,
the isotope effects on the quantities involved are not
independent.As an example, we consider the univer-
sal relation (11.40), predicting that close to the 2D–
QSI transition the isotope effect on transition tem-
perature and zero temperature in-plane penetration
depth are related by
ˇ
T
c
= ˇ
d
s
+ ˇ
1/
2
ab
(
0
)
, (11.71)
where
ˇ
B
=−
m
B
B
m
, (11.72)
where B denotes the shift of B upon isotope sub-
stitution. Although the available experimental data
on identical samples are rather sparse, the results
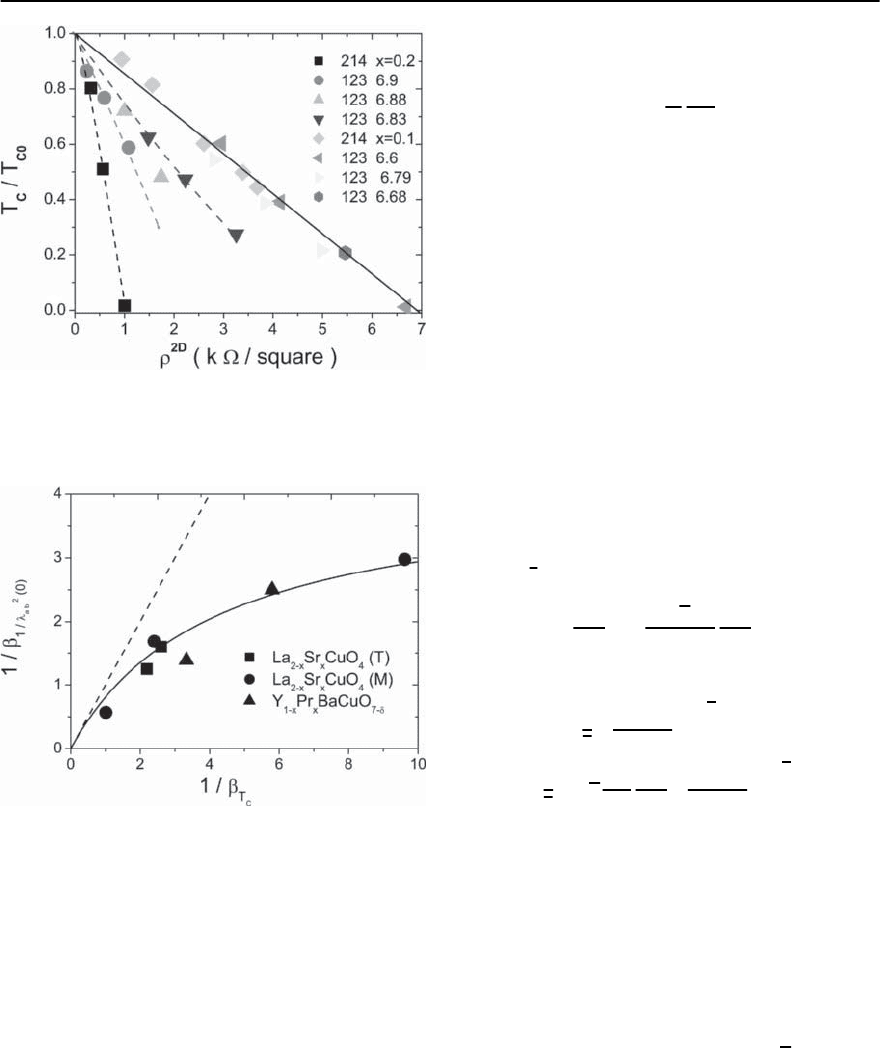
shown in Fig. 11.16 for the oxygen isotope effect
in La
2−x
Sr
x
Cu
1−x
O
4
[89,90] and Y
1−x
Pr
x
Ba
2
Cu
3
O
7
clearly reveal the crossover to the asymptotic 2D–
QSI behavior marked by the dashed straight line.The
solid curve is a fit to (11.71), yielding the estimate
ˇ
d
s
≈ −0.2 , (11.73)
for the isotope coefficient of d
s
. An essential result
is that the flow to 2D–QSI criticality implies that the
isotopecoefficientsˇ
T
c
and ˇ
1/
2
ab
(
0
)
diverge.Some in-
sight is obtained by noting that in the doping regime
of interest, isotope substitution does not affect the
dopant and substitution concentrations [89]. In con-
trast it lowers the transition temperature and shifts
the underdoped limit x
u
[34,92]. From the relation
T
c
= a ı
z
(see (11.38)), yielding
T
c
T
c
=−
z
x/x
u
−1
x
u
x
u
, (11.74)
we obtain for the isotope coefficient the expression
ˇ
T
c
=
1
r
T
c
(
x
m
)
T
c
1/z
, (11.75)
1
r
= z
m
m
x
u
x
u
a
T
c
(
x
m
)
1/z
,
applicable close to the 2D–QSI transition. Here we
rescaled T
c
by T
c
(
x
m
)
, the transition temperature at
optimum doping, to reduce variations of T
c
between
different materials [34].
In Fig. 11.17 we show the experimental data for
Y
1−x
Pr
x
Ba
2
Cu
3
O
7
[92], La
1.85
Sr
0.15
Cu
1−x
Ni
x
O
4
[93]
and YBa
2−x
La
x
Cu
3
O
7
[94] in terms of 1/ˇ
T
c
versus
T
c
/T
(
x
m
)
. As predicted by (11.76), approaching the
2D–QSI transition T
c
/T
c
(
x
m
)
= 0, the data collapse
on a straight line, pointing again to z
≈ 1(see
11.65)). Accordingly, the strong doping dependence
of the isotope coefficients of transition temperature
and zero temperature in-plane penetration depth in
11 Universal Properties of Cuprate Superconductors 477
Fig. 11.17. Inverse isotope coefficient 1/ˇ
T
c
versus T
c
/T
m
c
for Y
1−x
Pr
x
Ba
2
Cu
3
O
7
[92], La
1.85
Sr
0.15
Cu
1−x
Ni
x
O
4
[93] and
YBa
2−x
La
x
Cu
3
O
7
[94]. The straight line corresponds to
1/ˇ
T
c
= rT
c
/T
m
c
(see (11.76)) with z =1andr =6
Fig. 11.18. Magnetic field dependence of the specific heat
coefficient at zero temperature
c
T=0
for La
2−x
Sr
x
CuO
4
at
x=0.1, 0.16 and 0.22 (taken from Chen et al. [96])
underdoped cuprates follows naturally from the dop-
ing tuned 3D–2D crossover and the associated 2D–
QSI transition in the underdoped limit. One might
hope that this novel point of view about the isotope
effects in cuprate superconductors [95] will stimu-
late further experimental work to obtain new data to
confirm or refute these predictions.
A property suited to shed light on the critical be-
havior of both, the 2D–QSI and 3D–QSN transition
is the magnetic field dependence of the specific heat
coefficientin the limit of zero temperature. From the
scaling relation
c
T=0
∝ H
(
D−z
)
/2
c
(see (11.45)) it is
seen that for both transitions
c
T=0
∝ H
1/2
c
holds,
provided that z =1andz = 2 at 2D–QSI and 3D–
QSN criticality, respectively. The experimental data
displayed in Fig. 11.18 shows that in La
2−x
Sr
x
CuO
4
(
D − z
)
/2=1/2 holds irrespective of the doping
level. Thus these data provide rather unambiguous
evidenced for a 2D–QSI transition with z =1and
a 3D–QSN criticality with z =2.Thisimpliesthat
c
T=0
∝ H
1/2
c
is not a characteristic feature of d-
wave pairing, as proposed by Volovik [97] and Won
and Maki [98].
The above comparison with experiment provides
rather clear evidence for the occurrence of a 2D–
QSI transition with z =1and
=1intheun-
derdoped and a 3D–QSI critical point z =2and
=1/2 in the overdoped limit. Next, to substanti-
ate this scenario further, we consider the crossover
between these quantum critical points. Noting that
1/
2
ab
(
0
)
scales close to these critical points as (see
(11.38))
1
2
ab
(
0
)
∝ ¤
D
ab
(
0
)
∝ ı
((D−2+z
)
)
, (11.76)
we invoke
2
ab
(
0
)
=
a
x − x
u
+
b
(
x
o
− x
)
3/2
, (11.77)
to interpolate between the 2D–QSI and 3D–QSN
transition. A fit to the experimental data of
La
2−x
Sr
x
CuO
4
, yielding the parameters
a
=5.42 10
5
A
2
, b
=6.910
3
A
2
, (11.78)
is shown Fig. 11.19.
It is remarkable that this simple interpolation
scheme, reducing in the underdoped and overdoped
limit to the expected asymptotic behavior, describes
the data so well. Due to this agreement, this inter-
polation function provides in conjunction with the
empirical law for T
c
(
x
)
(see (11.2)), a realistic de-
scription of the doping dependence of the zero tem-
perature out-of-plane correlation
length
c
, given by (11.48), yielding
−
c
∝
T
c
2
ab
(
0
)
, close to 2D–QSI and 3D–QSN criticality.
The doping dependence of T
c
2
ab
(
0
)
is displayed in
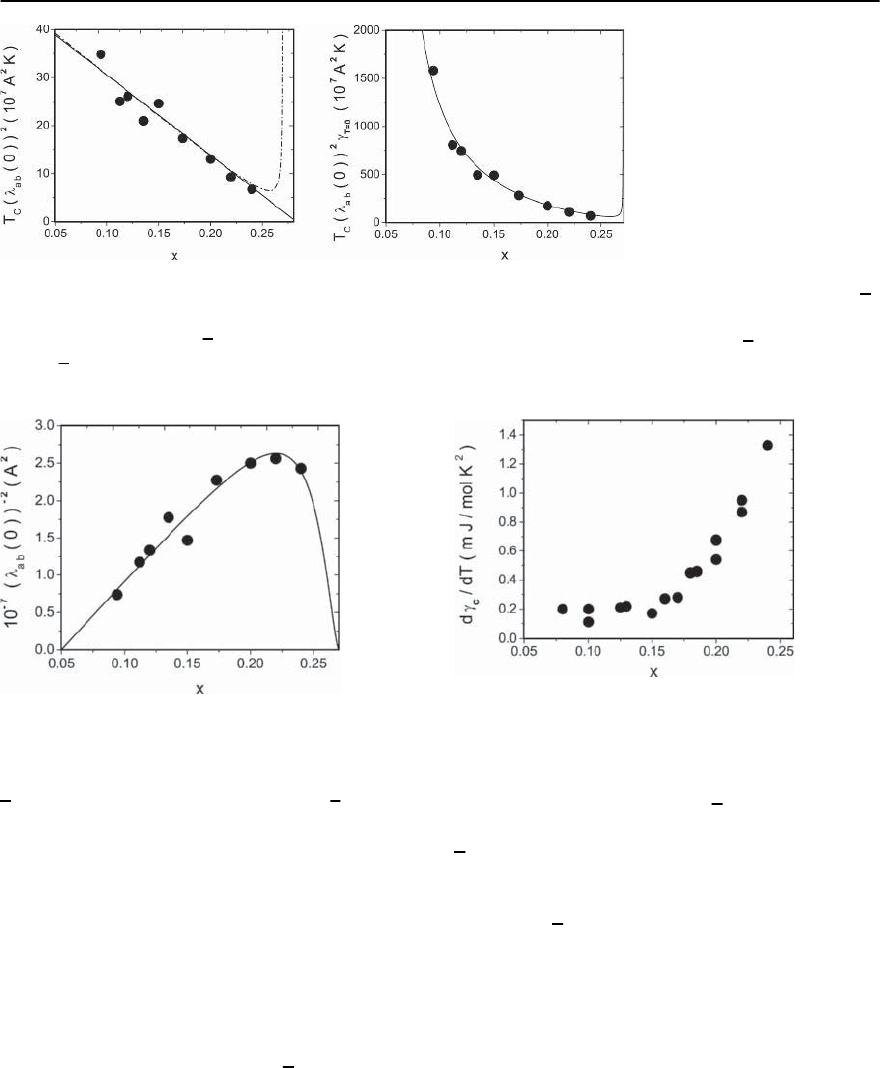
478 T. Schneider
Fig. 11.20. (a) T
c
2
ab
(
0
)
versus x for La
2−x
Sr
x
CuO
4
. •: taken from [9] and [83]. The solid line is (11.2) and (11.77) with
T
c
(
x
m
)
=39.8 K andtheparameters listedin (11.78).Notethat close to the 2D–QSI and 3D–QSN transition T
c
2
ab
(
0
)
∝
c
.
(b) T
c
−2
ab
(
0
)
T=0
versus x for La
2−x
Sr
x
CuO
4
. •: T
c
and
−2
ab
(
0
)
taken from [9,83] and
T=0
from (11.2) with
T=0,0
=2.
Note that T
c
−2
ab
(
0
)
T=0
∝
ab
(11.48). The solid curve indicates the crossover from 2D–QSI
(
z =1, =1
)
to 3D–QSN
(
z =2,
=1/2
)
criticality according to (11.2), (11.2),(11.76) and (11.77)
Fig. 11.19. 1/
2
ab
(
0
)
versus x for La
2−x
Sr
x
CuO
4
. •:experi-
mental data taken from [9,83]. The solid curve is a fit to
(11.77) with the parameters listed in (11.78). It indicates
the crossover from a 2D–QSI transition with z =1and
= 1 to a 3D–QSN criticality with z =2and =1/2
Fig. 11.20 for La
2−x
Sr
x
CuO
4
.SinceT
c
∝ d
s
/
2
ab
(
0
)
holds in the underdoped limit (see (11.40) and
Fig. 11.13), it is clear that T
c
2
ab
(
0
)
tends to a con-
stantvalue,proportional to d
s
,the thickness of the in-
dependent sheets. Since initially d/dx
T
c
2
ab
(
0
)
≈
−T
c
(
x
m
)
a
x
o
, the linear decrease simply reflects the
parabolic form of the empirical law (11.2). Finally,
the upturn close to the overdoped limit, a regime
which experimentally has not yet been attained, sig-
nals the 3D–QSN transition,where
c
∝ T
c
2
ab
(
0
)
di-
verges.In thiscontext it is also instructive to consider
the zero temperature in-plane correlation length. By
Fig. 11.21. T
c
d
c
/dT
T=0
versus x for La
2−x
Sr
x
CuO
4
.Data
taken from [15] and [99]
definition it diverges at a 2D and 3D quantum phase
transition. According to the scaling relation (11.48)
it can be measured in terms of
ab
∝ T
c
2
ab
(
0
)
T=0
.
In Fig. 11.20 we displayed the experimental data for
ab
∝ T
c
2
ab
(
0
)
T=0
versus x.Forcomparisonwe
included the behavior resulting from (11.2), (11.2),
(11.76) and (11.77) in terms of the solid curve.While
the rise of
ab
in the underdoped regime, signal-
ing the occurrence of a 2D–QSI transition, is well
confirmed, it does not extend sufficiently close to
the overdoped limit to detect 3D–QSN criticality.
From Fig. 11.21, showing the doping dependence of
the T-linear term of the specific heat coefficient of
La
2−x
Sr
x
CuO
4
, it is seen that this quantity tends to a
finite value in the underdoped limit and increases in
the overdoped regime. This behavior is fully consis-
