Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.


520 G. Blatter and V.B. Geshkenbein
with ∇·A = 0; the expressions ∇
(2)
,
(2)
,andA
(2)
de-
note the planar components of ∇,,andA).Equation
(12.101)is equivalent to the current conservation law
∇·j =0.
12.5.2 Josephson Vortices
We considera magnetic fieldin the ab-planepointing
along the y-directionand investigate the structureof
an individual Josephson vortex aligned with the y-
axis [61–63,194].We choose a gauge with A
y
=0and
A
x
, A
z
depending only on x and z. Subtracting the
phase equations (12.101) for n +1andforn from
each other provides a coupled set of equations for
the gauge invariant phase differences ¥
n+1,n
[78],
2
@
2
x
¥
n+1,n
=2sin¥
n+1,n
−sin¥
n+2,n+1
−sin¥
n,n−1
+
d
2
2
sin ¥
n+1,n
. (12.103)
Outside a core region with dimensions and d the
non-linearity and discreteness of the above equa-
tionsareirrelevantand(12.103)canbeapproximated
by the continuum differential equation
@
2
x
+ "
2
@
2
z
−
"
2
2
¥ (r)=0. (12.104)
Indeed, it is easy to see that the screening current
density along thez-axisin thecontinuumanisotropic
description,j
z
=−(2e/m)|¦ |
2
"@
z
˜' ≈ c¥
0
"/8
2
x,
becomes equal to the Josephson current density j
J
at
a distance x ∼ , hence for x > the linearized
continuum approximation provides a good descrip-
tion of the situation. On the other hand, for small
distances x < a further increase in the current
density j
z
is cut off by the condition |j
z
| < j
J
and the
discreteness of the problem becomes relevant.
Equation (12.104) tells us that the driving (gauge
invariant) phase differences vanish due to screen-
ing on a length /" along the x-axis and on a scale
along the z direction.Since the phase difference is the
quantity driving the currents we obtain a magnetic
size /" (along x)and (along z) for the Joseph-
son vortex, see Fig. 12.5. On these magnetic length
scales the Josephson and Abrikosov vortices in an
anisotropic superconductor are roughly equivalent.
Within the phasecore [63] with dimensions (along
x)andd (along z) we have to take the non-linearity
and the discreteness of (12.103) into account. On
these scales the phase is changing rapidly and the
current density j
z
reaches its maximum value j
J
at a
distance ∼ away from the axis of the vortex [194].
Furthermore, within this region the order parame-
ter is weakly suppressed in the layers adjacent to the
axis of the Josephson vortex: Ignoring thecoupling to
other layers, the Ginzburg–Landau equation for the
order parameter ¦
n
(¦
∞
n
=1)inthen -th layer reads,
2
e
−i'
n
∇
2
(|¦
n
|e
i'
n
)+|¦
n
| − |¦
n
|
3
= 0 ; (12.105)
separating into real and imaginary parts we obtain
for the real part
=
2
[
(2)
−(∇
(2)
'
n
)
2
]+1−|¦
n
|
2
>
|¦
n
| =0. (12.106)
If a Josephson vortex directed along the y-axis is
present between the n-th and the n +1-th layer
Fig. 12.5. Josephson vortex in a strongly layered superconductor. The usual normal core of the Abrikosov vortex (di-
mensions " and along z and x , respectively) is replaced by the phase core (dimensions d and = d/" along z and
x, respectively) within which the non-linearity and the discreteness of the problem is relevant. The region outside the
phase core is roughly equivalent to the corresponding regime in an Abrikosov vortex with screening currents extending
adistance along z and /" along x

12 Vortex Matter 521
the phase '
n
(x) will rapidly change on the scale
and we can approximate the derivative of the phase
@
x
'
n
≈ 1/. Combining this estimate with (12.106)
we obtain a suppression of the order parameter ¦
n
of
the order of ı|¦
n
|≈(/)
2
at the center (x =0)of
the Josephson vortex: contrary to the Abrikosov vor-
tex where the large current flow near the core leads to
a complete suppression of the order parameter, the
corresponding order parameter suppression in the
superconducting layers is only weak in the presence
of a Josephson vortex.
Note that the set of equations (12.103) for the
gauge-invariant phase differences ¥
n+1,n
can be gen-
eralized to an arbitrary field direction by substituting
the derivative @
2
x
with the planar Laplacian @
2
x
+@
2
y
and
completing the resulting equations with appropriate
boundary conditions describing the singularities in
the phase field produced by vortices penetrating the
layers [195]
∇
(2)
∧ (∇
(2)
¥
n+1,n
) ≡ @
x
@
y
¥
n+1,n
− @
y
@
x
¥
n+1,n
=2
ı(r − s
n+1
)−ı(r − s
n
)
, (12.107)
where s
n
denotes the position of the singularity in
the phase '
n
corresponding to the -th vortex in the
n-th layer.Notethat a straight vortex with s
n
= s
n+1
produces no driving singularity for the phase differ-
ences ¥
n+1,n
, i.e., no screening currents crossing the
layers are set up. It is quite remarkable that such a
closed set of equations involving only the gauge in-
variant phase differences ¥
n+1,n
can be found.
The Josephson vortex in a layered superconduc-
tor involves two length scales along the x-axis, the
core size = d/" and the magnetic size
c
= /".
This has to be contrasted with the Josephson vor-
tex in the junction between two weakly coupled bulk
superconductors, for which there is only one charac-
teristic length scale
J
=[c¥
0
/16
2
j
J
]
1/2
,with the
penetration depth of thebulksuperconductorsand j
J
the coupling current density of the junction.The dif-
ference can be understood in the following way: Con-
sider two bulk superconductorsjoined via a junction
with a coupling j
J
.Weplaceavortexlineintothe
junction and analyze its evolution from anAbrikosov
vortex at strong coupling j
J
≈ j
0
to a Josephson vor-
tex at weak coupling j
J
j
0
[196,197].As soon as the
translational symmetry is broken by the junction,the
structure of the Abrikosov vortex is modified as the
zero in the order parameter disappears and is re-
placed by a finite jump across the junction (this is
easily understood by solving the GL equation ¦ ≈
0 near the singularity with the boundary condition
¦
+
− ¦
−
= l@
x
¦
+
= l@
x
¦
−
, ¦
±
=(x +iy) ± l/2; the
length l is related to the transparency of the junction,
here chosen along the y-axis). Decreasing the cou-
pling j
J
belowj
0
the normalcoreof theAbrikosovvor-
tex is transformed into a phase core extending over a
distance
J
≈ (j
0
/j
J
) > along the junction where
the phase of the order parameter changes by ∼ 2.
As the current across the junction is limited to a value
j
J
< j
0
the order parameter suppression is reduced,
ı¦ ∼ (j
J
/j
0
)
2
, as compared to the complete order
parameter suppression in the Abrikosov vortex core.
With decreasing coupling j
J
the phase core expands
and the suppression of the order parameter becomes
small. Decreasing the coupling j
J
below the critical
value j
J
≈ j
0
/ the phase core expands beyond the
magnetic screening length and the transformation
to the Josephson vortex with only one length scale
J
describing the phase, the currents, and the field
across the junction has been completed. Upon a fur-
ther decrease in j
J
the order parameter suppression
then is reduced to the value ı¦ ∼ (j
J
/j
0
)/.
The analogous discussion for a layered supercon-
ductor produces quite a different result: In a layered
material, the screening currents flowing perpendic-
ular to the planes have to cross not only one sin-
gle junction but have to overcome the large num-
ber of /d junctions. Upon decreasing the coupling
strength between the layers the screening current
density along the c-axis is also reduced such that
the current pattern of the original Abrikosov vortex
immediately starts to expand along the junction.As
a result, the ratio between the magnetic extent of the
vortex and the size of its phase core remains always
the same, /
c
= d/ = const, independent of the
coupling strength,and we always keep the two length
scales and
c
describing the core and the magnetic
size of the Josephson vortex.
From the abovediscussion we can understand that
a Josephson vortex is very similar to an Abrikosov
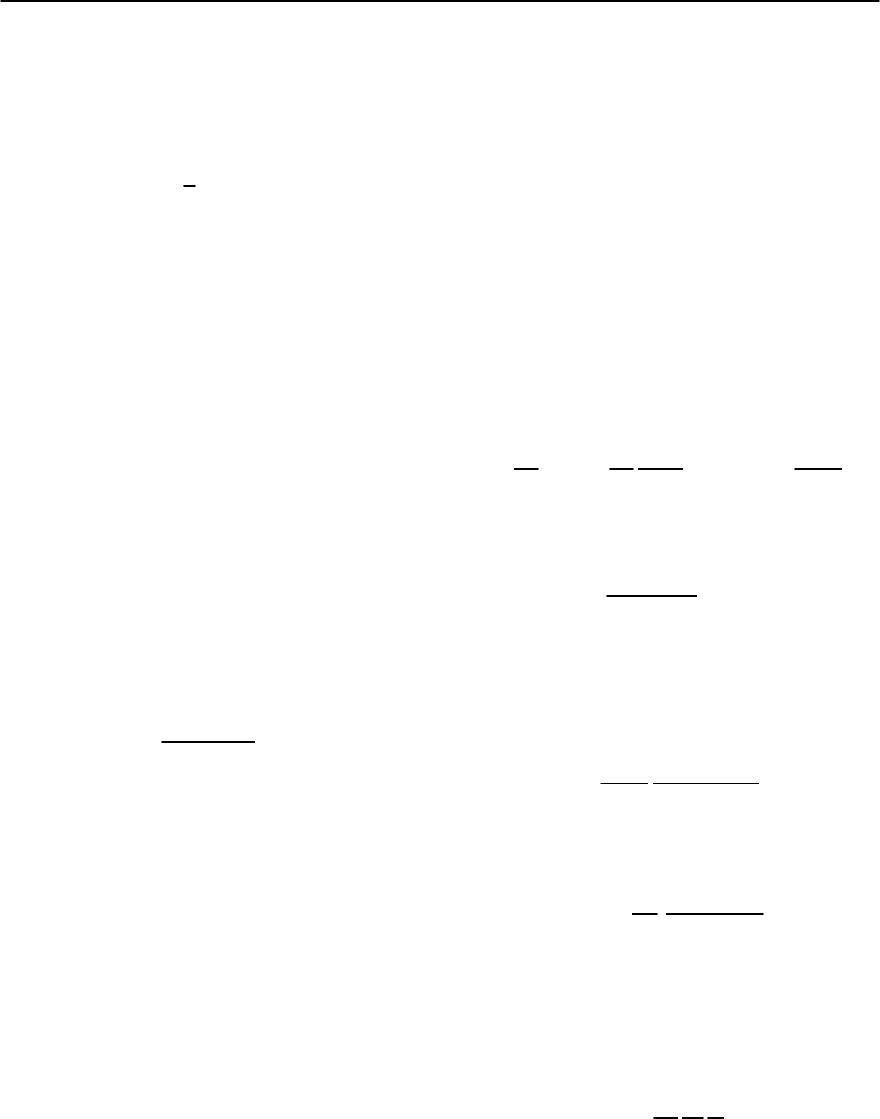
522 G. Blatter and V.B. Geshkenbein
vortex, however, with a different core size and struc-
ture.Thisconclusionisalsoconfirmedbythecal-
culation of the Josephson vortex line energy [61,62]
which is obtained through an integration of the ki-
netic energy of the currents
J
≈ ""
0
ln
d
+1.55
, (12.108)
where the inner and outer cutoff lengths in the log-
arithm are provided by the magnetic lengths (
c
, )
and the dimensions of the phase core (, d)ofthe
Josephson vortex (the constant 1.55 is found in a
more accurate analysis, see [198]). The correspond-
ing result for an Abrikosov vortex in an anisotropic
superconductor and directed along the planes is
[125]
l
= ""
0
[ln(/")+0.497]; note the different
temperature dependence for these two results aris-
ing from the substitution of
c
(T)="(T)bythe
layer distance d under the logarithm. The line en-
ergy (12.108) defines the lower critical fieldalong the
planes H
c
1
(# =0)=4
J
/¥
0
andthe (in-plane)elas-
tic tension of a Josephson vortex, "
l
=
J
.Finally,the
viscous drag coefficient depends on the core struc-
ture and differs only by a numerical factor from the
corresponding (Bardeen–Stephen) expression for an
Abrikosov vortex: substituting the appropriate di-
mensions for the phase core the result reads [199]
(see also [194])
J
≈ 1.8
¥
2
0
2
n
c
c
2
"
2
, (12.109)
with
n
c
the normal-state resistivity along the c-axis
and where we have assumed the relation
n
ab
= "
2
n
c
between thein-plane andc-axisresistivity (thecorre-
sponding Bardeen–Stephen result for the Abrikosov
vortex is
l
= ¥
2
0
/2
n
c
c
2
"
2
). In high-T
c
super-
conductors the resistivity–anisotropy relation is vi-
olated below T
c
and
n
ab
/
n
c
< "
2
; in this case the
in-plane dissipation is enhanced and we should re-
place
n
c
in (12.109) by the expression
n
c
/(0.79 +
0.21"
2
n
c
/
n
ab
) ≈ 4.76
n
ab
/"
2
.
12.5.3 Pancake Vortices
We consider a magnetic field directed along the c-
axis and discuss the structure of a vortex and its
planar constituents, the pancake vortices [65]. In
this context it is interesting to understand the sim-
ilarities and differences in the vortex structure for
the three cases of an isolated thin film [200], an un-
coupled stack of superconducting layers with j
J
=0
[62, 64, 65, 201,202], and a layered superconductor
with j
J
> 0 [64,195,201,203]. We start with the sim-
plest case of a 2D thin film of thickness d and choose
to denote the penetration depth of the correspond-
ing bulk material; the effective penetration depth of
the film is
eff
=2
2
/d. The solution for a vortex
positioned at the origin of the coordinatesystem has
been given by Pearl [200,204]: The London equation
(cf. (12.99); we write A
(2)
= A)
2
A = dı(z)(a + A) , (12.110)
with the source term
a =
¥
0
2
∇' =−
¥
0
2
ˆz ∧ R
R
2
, a
K
=i¥
0
ˆz ∧ K
K
2
,
(12.111)
is solved with the Fourier AnsatzA(r)=
d
3
k/(2)
3
× A
k
exp(ik · r),
A
k
=−
d(a
K
+ A
K
)
2
k
2
, with
A
K
=
d
2
R A(R, z =0)e
−iK ·R
, (12.112)
and an integration over k
z
provides the result A
K
=
a
K
/(1+
eff
K).Inserting this result back into (12.112)
we obtain
A
k
=−2i¥
0
ˆz ∧ K
K
1
k
2
(1 +
eff
K)
(12.113)
and transforming back to real space making use of
the cylindrical symmetry we find the vector potential
A
'
(R, z)=¥
0
∞
0
dK
2
J
1
(KR)e
−K|z|
1+
eff
K
, (12.114)
with J
1
(x) the Bessel function of integer order. The
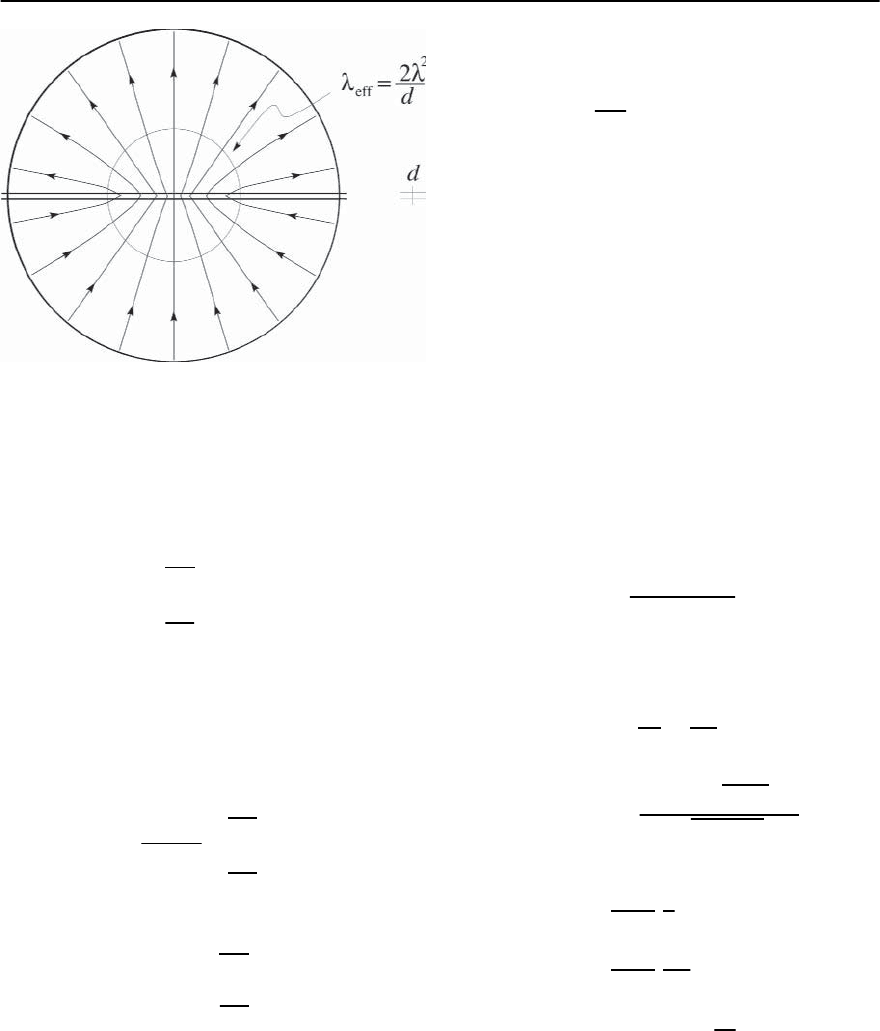
associated magnetic field asymptotically resembles
that of a positively/negatively charged magnetic
monopole generating a magnetic flux ¥
0
in the up-
per/lower half space, see Fig. 12.6,
B(r
eff
) ≈
¥
0
2
z
|z|
r
r
3
. (12.115)
12 Vortex Matter 523
Fig. 12.6. Pearl solution for a vortex in a superconducting
film with a magnetic field taking asymptotically the form
of a positively/negatively charged magnetic monopole in
the upper/lower half space
The magnetic flux crossing the film within a circle
of radius R is
¥ (R) ≈ ¥
0
⎧
⎪
⎪
⎨
⎪
⎪
⎩
R
eff
, R
eff
,
1−
eff
R
,
eff
R ,
(12.116)
andapproachesthe unit flux quantum ¥
0
at large dis-
tances. The circular current density J
'
(R)(perunit
length) decays algebraically with distance and gen-
erates (via the Lorentz force) a screened logarithmic
interaction V
int
(R) between a pair of Pearl vortices,
J
'
(R) ≈
¥
0
c
4
2
2
eff
⎧
⎪
⎪
⎨
⎪
⎪
⎩
eff
R
,
2
eff
R
2
,
V
int
(R) ≈ 2"
0
d
⎧
⎪
⎪
⎨
⎪
⎪
⎩
ln
eff
R
, R
eff
,
eff
R
,
eff
R .
Next, we discuss the case of an array of uncou-
pled (i.e., j
J
= 0) parallel superconducting layers
where the interaction is of electromagnetic origin
[62,64,65,201,202].Ignoring small variations in the
vector potential on the scale d we rewrite (12.99) in
the form (we use that A
(2)
= A)
[
2
−1]A =
d¥
0
2
n
ı(z − nd)∇'
n
. (12.117)
An individual vortex line threading the stack is char-
acterized by the positions S
n
of the vortex cores
within each layer. The gradients of the phase fields
∇'
n
(R)=−ˆz ∧ (R − S
n
)/|R − S
n
|
2
drive the screen-
ing currents in the individual layers, which in turn
are coupled electromagnetically through (12.117);
hence, screening currents in response to a pancake
vortex in the n-th layer will be set up within the other
layers of the stack.The linearity of (12.117) allows us
to reduce the problem to the analysis of the elemen-
tary building block of the vortex line, the pancake
vortex [62,64,65,201,202].We consider a single pan-
cakevortexwithitsdrivingfield∇'
n
(R)=−ˆz∧R/R
2
placed at the origin of the n-th layer (positioned at
z = 0) and with all the other driving terms vanishing.
Transforming (12.117) to Fourier space we find the
vector potential
A
k
=−id¥
0
ˆz ∧ K
K
2
(1 +
2
k
2
)
(12.118)
and transforming back to real space using cylindrical
symmetry we obtain the solution
A
'
(R, z)=¥
0
d
2
∞
0
dK
2
(12.119)
×
J
1
(KR)e
−
√
1+
2
K
2
|z|/
√
1+
2
K
2
.
The associated magnetic field (see Fig. 12.7)
B
z
(r)=
¥
0
4
2
d
r
e
−r/
,
B
(2)
(r)=
¥
0
4
2
d R
R
2
signz (12.120)
×
e
−|z|/
−
|z|
r
e
−r/
,
differs quite drastically from the monopole-likePearl
solution: The screening effect due to the other su-
perconducting planes in the stack squeezes the field
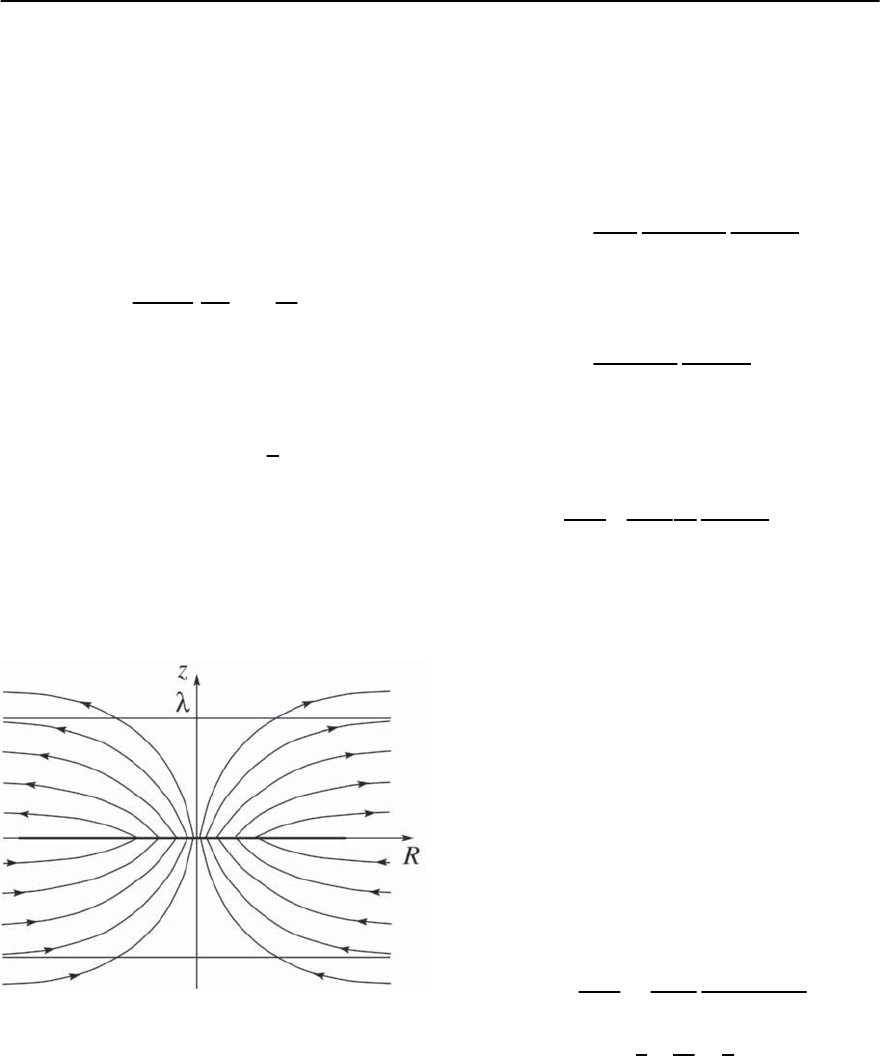
524 G. Blatter and V.B. Geshkenbein
into a layer of width along the z -axis and the mag-
netic field has to escape parallel to the layers rather
than spread out uniformly over the entire solid an-
gle. This field redistribution due to screening has
important consequences: First, the squeezing of the
field reduces the flux threading the central layer n to
¥ (R)=¥
0
(d/2)[1 − exp(−R/)] hence the current
flow is not able to screen the driving phase-field in
the central layer. Indeed, the current density of the
central layer decays like 1/R to all length scales,
J
'
(R, z =0)=
¥
0
c
4
2
2
eff
eff
R
1−
d
2
1−e
−R/
,
(12.121)
and therefore the logarithmic dependence of the in-
teraction potential V
int
between two vortices placed
in the same layer persists to infinity,
V
em
int
(R, z =0)=±2"
0
d ln
R
L
+ O(d/) ,
< R < L , (12.122)
with L the system-size cutoff (the − (+) sign refers to
equally (oppositely) charged vortices; note that the
total energy includes an additional self-energy term
2"
0
d ln(L/), with the bulk planar coherence length
serving as a short distance cutoff).
Fig. 12.7. Pancake vortex in a layered superconductor with
vanishing interlayer Josephson coupling. The screening
currents present in the neighboring layers squeeze the
magnetic field into the planar direction. The screening cur-
rent density in the central layer decays like j ∝ 1/R to all
scales
In order to find the general expression for the
interaction energy between pancake vortices (po-
sitioned at S
n
in layer z
n
= nd)weexpress
the current and magnetic field terms in the free
energy (12.97) through the current density j =
−(c/4
2
)[(¥
0
/2)d
n
ı(z − nd)∇'
n
+A ] and the
vector potential A, in Fourier space,
j
k
=−
c
4
2
id¥
0
ˆz ∧ K
K
2
2
k
2
1+
2
k
2
×
n,
e
−iK ·S
n
e
−ik
z
nd
, (12.123)
A
k
=−
id¥
0
ˆz ∧ K
K
2
1
1+
2
k
2
×
n,
e
−iK ·S
n
e
−ik
z
nd
; (12.124)
combining terms we arrive at the free energy
F =
¥
2
0
d
2
8
d
3
k
(2)
3
k
2
K
2
1
1+
2
k
2
(12.125)
×
n, ,m,
e
−iK ·(S
n
−S
m
)
e
−ik
z
(n−m)d
.
In order to make contact with the expressions (12.62)
and (12.80) describing interacting vortex segments
in the continuous anisotropic situation one has to
take the appropriate limit " → 0 and account for the
continuity of vortex lines via the relation ∇·s =0
(we remind the definition s
= r
+ u
of the vor-
tex positions), in Fourier space, K · S
k
=−k
z
s
zk
,
and hence S
˛,k
K
⊥˛
K
⊥ˇ
S
ˇ,−k
= K
2
|S
k
|
2
− |K · S
k
|
2
=
K
2
|S
k
|
2
−|k
z
s
zk
|
2
.Theterms∝|s
zk
|
2
in the freeenergy
(12.62) then combineinto a term |s
2
zk
k
2
/K
2
(1+
2
k
2
)
(cf.(12.126)),while those∝ (|s
xk
|
2
+|s
yk
|
2
)comewith
a prefactor 1/(1+
2
c
K
2
+
2
k
2
z
) which vanishes in the
limit " → 0.
An individual pancake vortex involves the energy
E
pc
=
¥
2
0
d
2
8
d
3
k
(2)
3
k
2
K
2
(1 +
2
k
2
)
= "
0
d
ln
L
−
d
2
ln
L
, (12.126)
where the first term is due to the driving term ∝∇'
and involves the core size as a short scale cutoff,
12 Vortex Matter 525
while the second term is due to screening. A vortex–
anti-vortex pair in the same layer (n) and separated
adistanceR costs an energy
E
+−
(R)=
¥
2
0
d
2
4
d
3
k
(2)
3
k
2
[1 − cos(K · R)]
K
2
(1 +
2
k
2
)
=2"
0
d
dK
1−J
0
(KR)
K
×
1−
d/2
√
1+
2
K
2
≈ 2"
0
d ln
R
, (12.127)
reproducing the result (12.122) above. Placing a sec-
ond pancake vortex (with equal phase turn) in layer
m we obtain the expression
E
++
(R, z)="
0
d
d
dK
J
0
(KR)
K
×
e
−
√
1+
2
K
2
|z|/
√
1+
2
K
2
, (12.128)
with R = |R
m
− R
n
| and z = z
m
− z
n
=(m − n)d.
In order to handle the (logarithmic) divergence at
small K (cf. the correction term in (12.126)) we de-
termine the (attractive) force f (R, z)=−@
R
E
++
(R, z)
between the two pancake vortices,
f = "
0
d
d
dKJ
1
(KR)
e
−
√
1+
2
K
2
|z|/
√
1+
2
K
2
. (12.129)
At very small distances R < |z| < the inte-
gral is cut by the exponential and we have f ≈
"
0
(d
2
/2
2
)(R/|z|);at intermediatescales|z| < R <
we find the constant force f ≈ "
0
d
2
/
2
;forlargedis-
tances < R the integral is cut by the J
1
factor and
f ≈ "
0
(d
2
/R). In the end we obtain an attractive in-
teraction between vortices which is small (by a factor
d/), but which is long ranged (extending over /d
layers),
V
em
int
(R, z = nd =0)≈ "
0
d
d
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎩
R
2
4|z|
, R |z| ,
R
, |z|R ,
ln
R
, R .
(12.130)
For separations |z| > the interaction decays ex-
ponentially ∝ exp(−|z|/) (the factor 1/2quoted
in [150] is incorrect).Finally,constructinga full vor-
tex line witha phase singularity present in each layer,
the calculation of the field distribution, the line en-
ergy, and the lower critical field H
c
c
1
[65] gives re-
sults in agreement with the continuous anisotropic
description,
B
z
=
¥
0
2
2
K
0
R
,
l
=
¥
0
4
H
c
c
1
= "
0
[ln +const.] . (12.131)
Similarly, the line energy
l
(# ) for a vortex tilted
by an angle = /2−# away from the c-axis
agrees (to logarithmic accuracy) with the continu-
ous anisotropic result (12.25) in the limit " → 0,
l
(# )="
0
sin # ln
sin #
1+sin#
2
(12.132)
(note that "
#
=sin# for the present case of perfectly
decoupled layers with " =0).
A finite Josephson coupling between the super-
conducting layers renders the introduction of a sin-
gle pancake vortex into the layered superconductor
impossible [64,195,201,203]: in addition to the elec-
tromagnetic interaction between the layers, the in-
terlayer Josephson coupling contributes the energy
F
J
=
d"
0
d
2
R
2
1−cos¥
n+1,n
(R
)
. (12.133)
The phase difference ¥
n+1,n
= 0 between the plane
containing the vortex and its two neighboringplanes
and the coupling energy F
J
to these two layers be-
comes infinite: ignoring a possible relaxation of the
phase pattern, equation (12.133) predicts an energy
of an individual pancake vortex which grows with

526 G. Blatter and V.B. Geshkenbein
the sample area. However, the phase pattern due to a
single pancake vortex can relax to a state with an en-
ergy growing only linearly in the sample size,the lin-
ear energy arising from the Josephson strings which
take the flux to and away from the pancake vortex.
Introducing a pair of oppositely “charged” pancake
vortices at a distance R into the same plane creates
two Josephson strings which contribute the energy
(12.133) with the phase differences ¥
n+1,n
(R
) deter-
mined by the coupled set of equations (12.101). In
ordertotruncatethissystemofequationsweassume
the phases '
n±1
to be undisturbed, while the phase
'
n
is distorted due to the presence of the pair in layer
n. The phase difference ¥ = '
n+1
− '
n
= '
n−1
− '
n
then is a solution of
2
(2)
¥ =−2sin¥ , (12.134)
where we have neglected the additional screening
term due to the vector potential which becomes rel-
evant on large scales R > /". For small phase dif-
ferences ¥ we can expand the sine in (12.134) and
we obtain the natural length scale (screening length)
= d/" of the problem. On scales R < the
Josephson currents cannot build up and the system
essentially behaves like an uncoupled layered mate-
rial with its ideal 2D behavior. On the other hand, for
distances R > the currents along z are no longer
hampered by the discreteness of the material and a
continuous anisotropic 3D behavior results.
At small separation R thesolutionof (12.134)
behavesas¥ (R R
) ≈ R·∇' =(R/R
)cos',
with ' = arctan(y/x) the azimuthal angle in the
plane,and vanishes ∝ exp(−R
/)atlargerdistances
R
.For small phase differences ¥ we can expand
the cosine in (12.133) and a trivial integration sup-
plies us with the Josephson interaction energy of the
pair,
V
J
int
(R) ≈ "
0
d
R
2
ln
R
, R . (12.135)
For large separations R , two Josephson strings
connecting the pair are created between the layers n
and n ± 1. The interaction between the two pancake
vortices then is dominated by the energies of the two
strings and takes the form (see (12.108))
V
J
int
(R) ≈ 2"
0
d
˛
R
−
4R
, R /" ,
(12.136)
with ˛ a numerical of order unity arising from cut-
ting off the logarithm in (12.108) at a distance of
the order of the separation d between the Josephson
strings [70,205].The last term in (12.136) is a higher
order correction to the leading string term (arising
again from the Josephson coupling[203]) and decays
exponentially at distances R > /".Thecomparison
of the Josephson interaction energies (12.135) and
(12.136) with the electromagnetic energy (12.122) of
the pair shows that the electromagnetic contribution
is larger at small distances R < and the Josephson
term dominates for distances R > .
In summary,we arrive at the following picturefor
the interaction between two pancake vortices placed
inthesamelayerofaJosephsoncoupledsystem:At
small distances R < the Josephson currents have
not yet built up, the electromagnetic energy is dom-
inant and we obtain a logarithmic interaction. As R
grows beyond , the Josephson currents have been
established, the magnetic field between the two vor-
tices has been redirected into two Josephson strings
and the interaction grows linearly, i.e., the pair be-
comes confined.
Two further pancake-vortex configurations are
the kink–anti-kink excitation along one Josephson
vortex [203] with the energy
V
K,−K
int
(R) ≈ 2"
0
d
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎩
ln
R
, < R < ,
ln
−
4R
, < R < /" ,
ln
, /" < R ,
(12.137)
and the double-kink configuration providing the
building block of a tilted vortex with an energy
[201] (we assume < ; otherwise, the linear term
∝ dR/
2
saturates at R ∼ , cf. (12.130))
V
K,K
int
(R) ≈ "
0
d
⎧
⎪
⎪
⎨
⎪
⎪
⎩
d
R
+
1
2
R
2
ln
R
, < R < < ,
2R
, < R < /" .
(12.138)
12 Vortex Matter 527
These basic pancake-vortex configurations allow to
study more complicated vortex configurations and
their energies in terms of point-like interacting par-
ticles. An example is the calculation of the line en-
ergy for a tilted vortex from which we can find the
elastic line tensions for the in-plane and for the out-
of-plane tilt modes: Summing up the energies of the
individual pancake vortices including their interac-
tion as given by (12.138) and the contributions from
the Josephson strings (12.135) and (12.136) we find
the line energy of a vortex tilted by an angle # with
respect to the layers.For large angles # > " the sep-
aration between neighboring pancake vorticesis less
than and the line energy becomes [195,206]
l
(# > ")="
0
sin # (12.139)
×
ln
˛
sin #
+
"
2
2tan
2
#
ln
˛
tan #
d
,
where ˛ and ˛
are numericals of order unity. For
small angles 0 < # < ", the Josephson string con-
tributesa large energy (12.136) and the result reads
l
(0 < # < ")="
0
sin # (12.140)
×
ln
+
"
tan #
ln
d
+
1
2"
tan #
.
Using the definitions (12.37) for "
⊥
l
and for "
l
above
we easily find the expressions for the out-of-plane
and the in-plane line tensions in a layered mate-
rial [150] (we ignore logarithmic corrections and
the divergence of "
⊥
l
due to the lock-in transition
[207–209] at # =0):
"
⊥
l
(# )=
"
0
"
⎧
⎪
⎪
⎨
⎪
⎪
⎩
1
cos
3
#
, 0 < # < " ,
"
3
sin
3
#
, " < # <
2
,
"
l
(# )=""
0
⎧
⎪
⎨
⎪
⎩
cos # , 0 < # < " ,
"
sin #
, " < # <
2
.
These equations strongly resemble the results for the
anisotropic superconductor, a consequence of the
similarity in the current flow set up by a vortex in
an anisotropic and in a layered material.
12.5.4 Renormalized Superfluid Stiffness
The presence of pancake vortices leads to a down-
ward renormalization of the superfluid density in
the superconducting layers [76,210]; this effect has
various consequences for the structural and statis-
tical properties of the vortex system in layered su-
perconductors, such as a reduction in the effective
anisotropy, a modification of the characteristics of
the Josephson vortices,andimplicationsfor the layer
decoupling transition. Strictly speaking, in the ab-
sence of pinning the presence of pancake vorticesre-
moves the (homogeneous) superfluid stiffness alto-
gether. However,a finite superfluid stiffness survives
at finite distances: we can define a short-wavelength
(k
z
≈ /d) superfluid stiffness J in an individual
superconducting layer. This stiffness J(K)isdisper-
sive, where the (in-plane) long-wavelength limit J(0)
is determined by the pinning of the pancake vortices
within the pancake-vortex stacks produced by the
vortices in the other layers; its dispersive component
∝ K
2
is due to the finiteshear energy associated with
the deformation of the pancake-vortex lattice in the
plane.
In order to gain a better understanding of this
renormalized in-plane dispersive phase stiffness we
search for a free energy functional ıF[ıA, u]de-
scribing the stiffness of the gauge-invariant vector
potential ıA in the presence of mobile vortices de-
scribedby their displacement field u (wefirst concen-
trate on a 2D (translation invariant) situation with
the field B ˆz); note that ıF and ıA describe the
deviations in the free energy and in the gauge field
with respect to the equilibrium vortex lattice state.
In particular, the gauge field ıA contains a term
−j/
s
,
s
≡ c/4
2
= e
2
n
s
/mc, originating from the
(macroscopic) current density j and a second term
u ∧ B due to the vortex displacement u, originating,
e.g., in response to an applied external current den-
sity j
ext
,
ıA =−
1
s
j + u ∧ B . (12.141)
Here, the field B ˆz generates the vortices re-
ducing the superfluid stiffness. The vortex-induced
gauge potential is easily understood in the dynam-
ical situation: taking the derivative of ıA
u
= u ∧ B
528 G. Blatter and V.B. Geshkenbein
with respect to time we find the Josephson relation
ıE =−@
t
ıA
u
/c = B ∧ v /c with the vortex velocity
v = @
t
u. Alternatively, the relation ıA
u
= u ∧ B fol-
lows from explicit calculation of the distortionin the
vortex phase fieldı'
v
= '
v
(R−u)−'
v
(R) ≈ −u·∇'
v
and suitable average over areas ıA > a
2
0
: using the
definition∇'
v
=−
ˆz ∧(R − S
)/|R − S
|
2
,where
S
denote the vortex positions, and transforming to
Fourier space one finds the useful relations
u
K
=
a
2
0
2
(ˆz ∧ iK)
ı'
vK
,
ı'
vK
=
2
a
2
0
(u
K
∧ iK) ·ˆz
K
2
. (12.142)
Substituting iK
ı'
vK
→∇ı'
vK
→ (2/¥
0
)ıA
u
one easily reproduces the relation ıA
u
= u ∧ B.
The free energy functional we are searching for
then should contain terms describing the kinetic and
magnetic energies associated with ıA and terms ac-
counting for the elastic energy following from the
displacement field u; indeed, the free energy density
ıf [ıA, u]=
1
8
(∇∧ıA)
2
+
1
2
ıA − u ∧ B
2
+
c
66
2
[∇⊗u]
2
(12.143)
exhibits all the correct features (the tensor product
in (12.143) stands for [∇⊗u]
2
≡ @
x
˛
u
ˇ
@
x
˛
u
ˇ
): i)
Variation with respect to the vector potential ıA re-
produces the relation (12.141). ii) “Integrating” over
the gauge field ıA viaminimizingwith respect to ıA,
ıA
K
=
u ∧ B +
2
K [K · (u ∧ B)]
1+
2
K
2
, (12.144)
and inserting the result back into (12.143), we find
the elastic energy density ıf
el
=(1/2){[c
11
(K)−
c
66
] |K · u
K
|
2
+ c
66
K
2
|u
K
|
2
} with the correct modu-
lus c
11
(K)−c
66
=(B
2
/4)/(1 +
2
K
2
) (note that
we should identify (B
2
/4)/(1 +
2
K
2
)withthe
combination c
11
(K)−c
66
, cf. [13] and the remark
below (12.68); the tensor product in (12.143) then
transforms to c
66
K
2
|u
K
|
2
/2 and the combination
c
66
[K
2
|u
K
|
2
− |K · u
K
|
2
]=c
66
|K ∧ u
K
|
2
). And iii),
variation with respect to u produces the force equa-
tion
1
c
j ∧B =−c
66
∇
2
u , (12.145)
where j accounts both for current densities applied
externally as well as those induced internally via
compression. Note that the kinetic energy of the
smooth macroscopic currents (external and from
vortex lattice compression) enter the free energy
density (12.143) via the term ∝
−2
,whereasthe
small microscopic currents due to the distortion u
of the vortex system are accounted for in the shear
term.
Further insight into the nature of the superfluid
stiffness in the presence of vortices is gained when
the force equation (12.145) is modified to account
for vortex pinning: using the Labusch [6] parame-
ter ˛
L
we introduce an effective pinning force den-
sity f
pin
=−˛
L
u balancing the Lorentz force density
j
ext
∧ B/c (note that the elastic forces due to shear
and compression are taken care of in the effective
pinning parameter ˛
L
). Inserting the displacement
field u = j
ext
∧B/c˛
L
back into (12.141) we find that
the response j
ext
=−
eff
s
ıA involves the renormal-
ized superfluid density
eff
s
=
c
4
1
2
+ B
2
/4˛
L
; (12.146)
as expected, in the absence of pinning, ˛
L
→ 0, the
effective superfluid density
eff
s
→ 0 vanishes. The
renormalized superfluid density (12.146)defines the
Campbell penetration depth
C
=
2
+ B
2
/4˛
L
describing the penetration of a static external signal
into the superconductor in the presence of (pinned)
vortex lines [211].On the other hand, accounting for
the finiteshear forcein (12.145) the same calculation
provides the dispersive response
eff
s
(K)=
c
4
2
1
1+16/a
2
0
K
2
≈
c
4
2
a
2
0
K
2
16
.
(12.147)
Next, we modify (12.143) to describe our pancake
vortex system in a layered superconductor (we as-
sume that B ˆz). We separate the term describing
the smooth macroscopic current flow in the planes
and complete with the elastic and Josephson cou-
pling terms,
12 Vortex Matter 529
ıF =
1
8
d
3
r
×
(∇∧ıA)
2
+
1
2
ıA
(2)
− u ∧ B
2
+
d
2
R
n
×
c
66
2
[∇⊗u
n
]
2
+
v
em
2
u
2
n
+
"
2
"
0
d
1−cos¥
n+1,n
, (12.148)
where the shear energy is determined by the density
of pancake vortices n
pc
= B/¥
0
= a
−2
0
, c
66
= "
0
d/4a
2
0
.
The electromagnetic component of the tilt energy
(12.85) is strongly dispersive ∝ k
−2
z
and turns the
elastic tilt energy into a potential term with a pref-
actor v
em
≈ ("
0
d/2a
2
0
2
)ln[a
2
0
/(d
2
+ u
2
)], where we
have assumed k
z
∼ 1/d in the logarithm.Finally,a fi-
nite Josephson coupling between layers is accounted
for within a Lawrence–Doniach type description (cf.
(12.97)) and involves the gauge invariant phase dif-
ference ¥
n+1,n
.
Inordertofindtheeffectivefree energy describing
the gauge invariant vector potential ıA we integrate
over the displacement field u in (12.148); the rele-
vant terms involving the displacement field define
the partial free energy density
ıf
n
=
2"
0
d
a
4
0
×
A
(2)
K
− u
K
∧ B
2
B
2
(12.149)
+
a
2
0
K
2
16
|u
K
|
2
+ g |u
K
|
2
.
The first term describes the kinetic energy density
of the smooth macroscopic current flow. The second
term describes the shear stiffness and the third con-
tributionoriginatesfrom the electromagnetictilt en-
ergy which “binds” the pancake vortices into stacks;
here, we have rewritten the electromagnetic tilt en-
ergy in the form g (2"
0
d/a
4
0
)|u
K
|
2
with the reduc-
tion factor
g =
a
2
0
8
2
ln
a
2
0
d
2
+ u
2
0
; (12.150)
the displacement u
0
in (12.150) is determined by the
pancake displacement typical for the actual physical
situation (e.g.,see (12.159) below). Note that it is this
“pinning” via the pancake vortex stack which will
establish a finite short-wavelength superfluid den-
sity in the individual layers. Finally, we “integrate”
over the displacement field u: minimizing (12.150)
we find
u
K
=
B ∧ ıA
(2)
B
2
1
1+a
2
0
K
2
/16 + g
(12.151)
and inserting this solution back into (12.150) we ob-
tain the free energy density
ıf
n
[ıA]=
d
8
2
g + a
2
0
K
2
/16
1+g + a
2
0
K
2
/16
|ıA
(2)
K
|
2
,
(12.152)
from whichwefindtherenormalizedsuperfluidstiff-
ness
eff
s
(K)=
c
4
2
g + a
2
0
K
2
/16
1+g + a
2
0
K
2
/16
. (12.153)
Comparing with (12.146) we can trace back the fi-
nite long-wavelength superfluid stiffness ∝ g/(1+g)
to the out-of-plane pinning action of the pancake
vortex stacks with the effective Labusch parame-
ter ˛
L
=4g"
0
/a
4
0
derived from the “pinning” po-
tential V
pin
= ˛
L
u
2
/2 due to the electromagnetic
interaction defining the stacks. Similarly, compar-
ison with (12.147) shows that the dispersive con-
tribution ∝ a
2
0
K
2
/16 is due to the in-plane vor-
tex shear energy. The full result (12.153) then fol-
lows from the combination of the force equation
j ∧ B d/c =(v
em
+ c
66
K
2
) u with (12.141).
Finally,wederive an expression for the free energy
in terms of the phase variable
ı' through the substi-
tution ıA
(2)
→ (¥
0
/2)∇ı' (the overline reminds
us that ıA
(2)
and hence also ∇ı' are smooth fields
averaged over distances larger than the vortex lat-
tice spacing); expanding (12.152) in a
2
0
K
2
/16 and
combining with (12.148) we arrive at
