Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.

1462 D. Manske,I. Eremin, and K.H.Bennemann
particles couple strongly to spin fluctuations. Most
importantly, as follows from Fig. 23.20, the largest
scattering will occur at values of k − k
F
= Q and
! = !
sf
. From (23.170) it follows that
£(k, i!
n
)=−T
2
!
m
,
m
k
,q
˜
0
× G(k − k
, i!
n
− i
m
)˜
0
U
2
×
1
2
Tr
[
˜
0
G(k + q, i!
m
+ i
m
)˜
0
× G(q, i!
m
)
]
. (23.125)
Then approximating the Green’s function
G(k, i!
n
) ≈ G
0
(k, i!
m
)=
i!
n
˜
0
+
k
˜
3
−
k
˜
1
(i!
n
)
2
− E
2
k
,
(23.126)
aftersomealgebraoneobtainswithE
2
k
=
2
k
+
2
k
on
the real axis
£(k, !) ≈ −
U
2
4
k
∞
0
d!
Im
RPA
(k − k
, !
)
! − !
− E
k
×
coth
!
2T
−tanh
!
− !
2T
.
(23.127)
In a simple view, in which the feedback effect of
superconductivity on is neglected, the imaginary
part of the spin susceptibilityis approximately given
by the Ornstein–Zernicke expression, which has a
peak structure at the wave vector q and frequency
! = !
sf
. Furthermore, the self-energy is mainly
frequency-dependent, while the bare dispersion of
the carriers is not. Then, already in the normal state
the self-energy £(k, !) has a maximum reflecting
acorrespondingmaximumofIm at q ≈ Q and
!
≈ !
sf
. Then, the kink position follows from the
pole of the denominator of (23.127).Thisleads to the
“kink condition”
!
kink
≈ E
k−Q
+ !
sf
(x) . (23.128)
Note that this gives an estimate of the position of the
kink and explains the behavior of the spectral den-
sity A(k, !) shown in Fig. 23.34. Furthermore, since
thesuperconducting gap is zerofor ! = 0,but notfor
! = !
sf
, the kink feature along the nodal direction
(0, 0) → (, ) will change only slightly below T
c
.
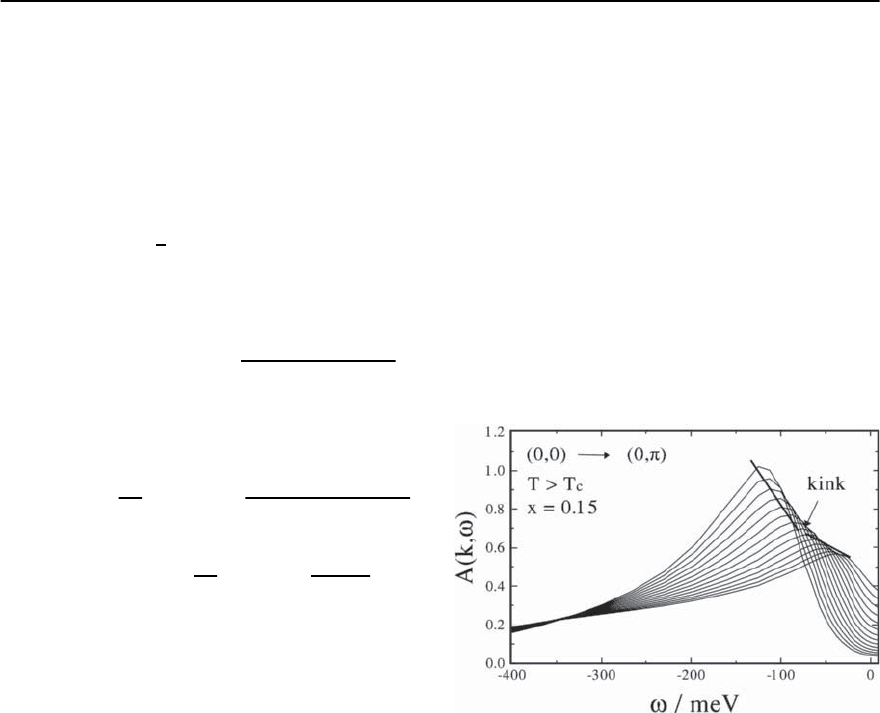
2. (0; 0)−! (0;) Direction
In order to see whether the kink feature is present in
otherdirections of theBrillouinZone,in Fig.23.35 we
show the evolution of the spectral density along the
(0, 0) → (0, ) direction. Despite the fact that along
this direction we do not cross the Fermi level, the
kink feature is still present and is found at an energy
similar to the one for the nodal (0, 0) → (, )-
direction. This indicates that the kink feature occurs
not only along the (0, 0) → (, )-direction. In-
stead,the kink is characteristic for all direction where
k − k
F
Q and ! !
sf
.Also belowT
c
we find that
the kink feature is present in the (0, 0) → (0, )-
direction (not shown). Note that our results are in
fair agreement with experimental data [46].
Fig. 23.35. Spectral density A(k, !) as a function of fre-
quency along the (0, 0) → (0, ) direction of the first BZ
in the normal state calculated from the generalized Eliash-
berg equations.Again, the peak positions reveal the renor-
malized energy dispersion !
k
.A kink occurs at similar en-
ergy as in the nodal direction.Due to inelastic scattering of
holes by spin fluctuations close to (0, ), A(k, !)alsobe-
comes broader.Note that,in contrast to the nodal direction,
one does not cross the Fermi level in the (0, 0) → (0, )-
direction. Instead, one reaches the flat part of the tight-
binding band
3. AntinodalDirection
In Fig.23.36(a) we show our results for N(k, !)along
the (, 0) → (, )route,i.e.theantinodaldirec-
tion, of the first BZ in the normal state. Note, that the
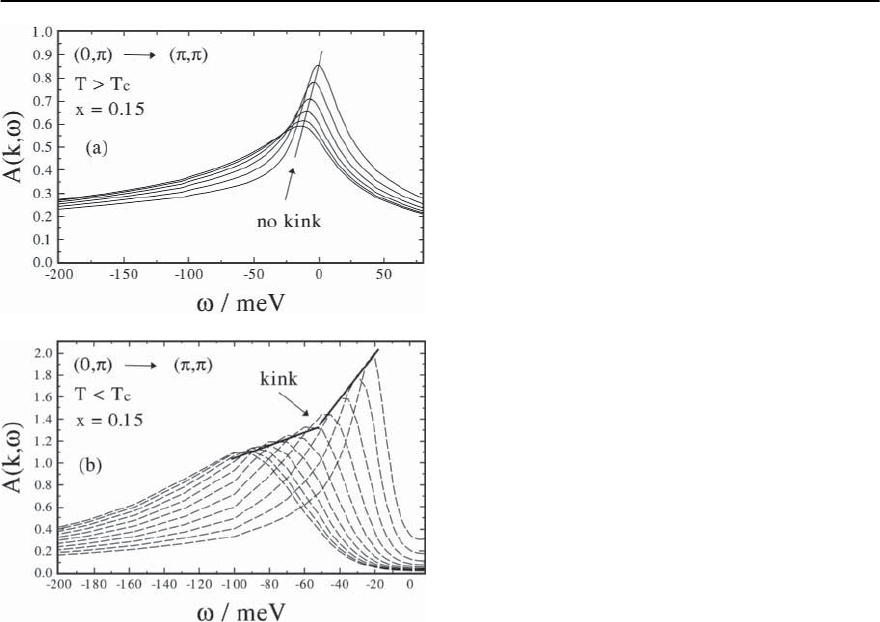
23 Electronic Theory for Superconductivity 1463
Fig. 23.36. Calculated spectral density A(k, !) along the
antinodal ( , 0) → (, ) direction in the first BZ as a
function of frequency in the normal (a) and superconduct-
ing (b) state. Due to the flat band close to the Fermi level
the spectral density shows no kink structure in the normal
state. Below T
c
the superconducting gap (!)opensyield-
ing a kink structure in the spectral density that occurs at
the energies !
kink
≈ 50 ±10 meV for optimal doping
spectral density at the (0, ) point is broader than at
the antinodal point due to stronger coupling to spin
excitations peaked at q = Q =(, ) as discussed in
Fig. 23.20. Clearly, no kink is present.
The absence of a kink structure can be explained
with the flat structure of the CuO
2
-plane around the
M point (see Fig. 23.32) and with the fact that the
wavevector is not large enough to bridge antinodal
points in the BZ. Simply speaking, for a flat band the
frequency dependence of £ in (23.32) does not play
a significant role and therefore no change of the ve-
locity and no kink structure is present.
What happens in the superconducting state? Be-
low T
c
the superconducting gap (k, !)opens
rapidly for decreasing temperature T and becomes
maximal in momentum space around the M point
reflecting the momentum dependence of the effec-
tive pairing interaction (see (23.170)). In addition,
due to the frequency dependence of the gap the flat
band around M disappears.
In Fig. 23.36(b) we show results for A(k, !)ata
temperature T =0.5T
c
where the superconducting
gap has opened. A kink structure around !
kink
≈
50 ± 10 meV is present reflecting the magnitude of
. Hence, in the (, 0) → (, ) direction this kink
feature is only present below T
c
and connected to the
feedback effect of on the elementary excitations.
We will show later that this feedback is also impor-
tant for the resonance peak seen in INS. Note that
the superconducting gap (k, !)iscalculatedself-
consistentlyin our theory and reflectingthe underly-
ing spin fluctuations which dominate the pairing po-
tential V
eff
.Therefore,the occurrence of a kink struc-
ture only below T
c
in the antinodal direction is a di-
rect fingerprint of the spin excitation spectrum. Fur-
thermore, as we will discuss below, Im (Q, !)en-
tering (23.127) is peaked at the resonance frequency
!
res
. Therefore, the kink condition is given by
!
kink
≈ E
k−Q
+ !
res
(x) . (23.129)
In Fig. 23.37(a) the frequency dependence of
Re £(k
a
, !) in the normal and superconducting state
at the antinodal point k = k
a
is shown. Due to the
occurrence of the resonance feature in Im (Q, !)
and the related feedback of the superconducting gap
(!), Re £ shows a pronounced structure below T
c
at energies of about !
res
+
0
. Also the correspond-
ing imaginary part Im £(k = k
a
, !)showsapeak
below T
c
(see Fig. 23.37(b)). This pronounced be-
havior is responsible for the kink formation along
(, 0) → (, ) direction in the BZ.
Therefore, while the kink features are present
along (0, 0) → (, )and(, 0) → (, )-direc-
tions in the superconducting state of hole-doped
cuprates,their nature is qualitatively different.Along
the nodal direction the superconducting gap is zero
(for ! = 0) and thus the feedback effect of super-
conductivity on the elementary and spin excitations
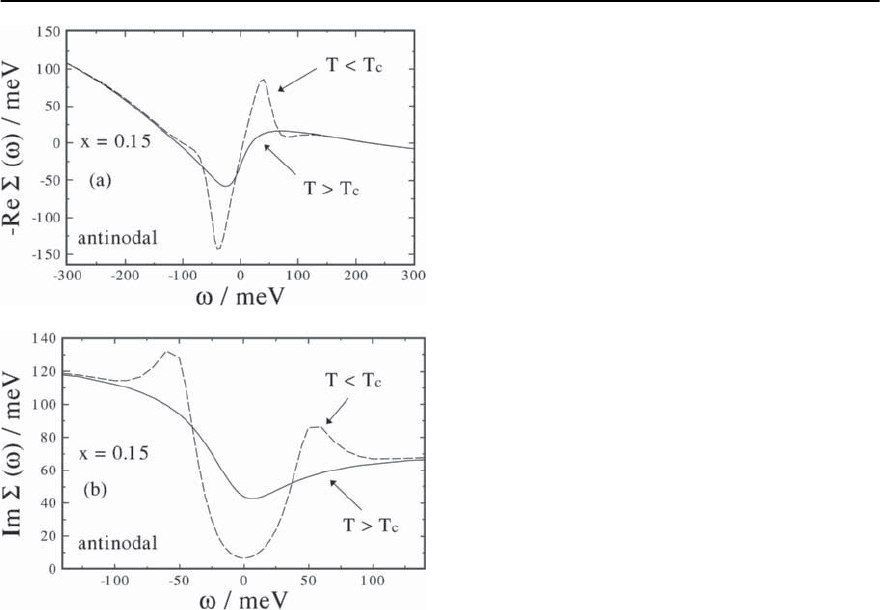
1464 D. Manske,I. Eremin, and K.H.Bennemann
Fig. 23.37. (a) Calculated frequency dependence of the self-
energy Re £(k
a
, !)attheantinodalpointk
a
of the first
BZ in the normal (solid curv e) and superconducting state
(dashed curve). Due to the feedback effect of the supercon-
ducting gap (!), a peak (dip) occurs for ! > 0(! < 0),
which roughly defines the position of the kink structure.
(b) The corresponding imaginary part at the antinodal
point Im £(k = k
a
, !) is shown. Again, due to the feed-
back effect of (!), a maximum occurs below T
c
.Notethat
both Re £ and Im £ are not fully antisymmetric (symmet-
ric) with respect to ! at optimum doping x =0.15
is small. Therefore, !
sf
determines mainly the kink
feature.On the other hand,along the antinodal direc-
tion the gap is maximal and yields a strong feedback
of superconductivity on . Thus, in the supercon-
ducting state !
res
and
0
yield the kink structure
along (, 0) → (, ) direction that is not present
in the normal state.
Doping Dependence of the Elementary Excitations and
Their Energy Renormalization
The different reasons for the kink structuresin hole-
doped cuprates along different directions in the first
BZ will be also reflected in their doping dependence.
The results we have shown so far were for optimal
doping concentration x =0.15. This refers to a band
filling of n =0.85. Note that the superconducting
transition temperature T
c
behaves differently in the
overdoped (OD) and underdoped (UD) regime:
T
c
∝ (T → 0), OD-regime
T
c
∝ n
s
(T → 0), UD-regime,
where n
s
is the superfluid density calculated self-
consistently from the generalized Eliashberg equa-
tions.
In the antinodal (0, ) → (, )-direction the
kink is only present below T
c
due to the feedback
of (!). In the OD case the gap (!) decreases re-
flecting a mean-field-like behavior.Thus, the energy
where the kink occurs must decrease with overdop-
ing:
!
kink
(x) ∝
0
(x) . (23.130)
This behavior was indeed observed by Dessau and
co-workers [74]. Note that the above argument re-
mains true also in the strongly OD case where no
resonance peak in Im (Q, !)occursbecausethe
feedback effect of (!) should always be present.
Regarding the kink along the nodal (0, 0) →
(, )-directionwe note the following: !
sf
increases
with increasing doping from underdoped to over-
doped cuprates. Since !
sf
determines the kink posi-
tion along (0, 0) → (, ) direction we expect
!
kink
(x) ∝ !
sf
(x) . (23.131)
This is in qualitative agreement with experimen-
tal data [120] (for underdoped regime and opti-
mally doped superconductors). On the other hand,
the spectral weight of Im (Q, !) decreases dras-
tically with overdoping. Therefore, the coupling of
the quasiparticles tospinfluctuationsbecomesmuch
weaker in the OD case. These two competing effects
seem responsible for the non-monotonic and weak
doping dependence of the kink position in the nodal
direction [74].

23 Electronic Theory for Superconductivity 1465
Elementary Excitations in Electron-Doped Cuprate
Another interesting observation is the asymmet-
ric behavior of hole and electron-doped cuprates.
Note that no kink feature has been reported in
the electron-doped cuprates [48]. It is believed that
the electron–phonon coupling is much more pro-
nounced in electron-doped cuprates than in hole-
doped ones. This is reflected, for example, by the be-
havior of the resistivity ∝ T
2
in the normal state
at optimum doping and by the transition between
d
x
2
−y
2
-wave symmetry of the superconducting gap
towards anisotropic s-wave, as has been observed in
several experiments [121]. Simply speaking, the spin
fluctuations in electron-doped cuprates are weaker
than in the hole-doped ones, yielding a smaller T
c
and a smaller superconducting gap [122]. Thus, no
kink is present in the nodal direction and also no
kink occurs in the (0, ) → (, )-direction below
T
c
.This is related to the fact that the flat band around
(0, ) lies in electron-doped cuprates well below the
Fermi level and, therefore, it cannot be softened due
to (!).
Summary
Regarding the superconducting state note that in the
hole-doped cuprates a strong renormalization of the
spin fluctuation spectra occurs due to the feedback
effect of superconductivity. (Note that this leads also
to a resonance peak at ! = !
res
.) In electron-doped
cuprates, only a rearrangement of spectral weight
occurs below T
c
.Note that the kink feature is inti-
mately connected with the resonance peak result-
ing for Im , see the discussion below. There is only
a small feedback of superconductivity below T
c
on
Im in theelectron-doped cupratesdueto !
sf
0
.
Thus, we find no kink feature in the superconduct-
ing state of electron-doped cuprates in the antinodal
direction. Due to correlations the hole-doped and
electron spectral density is different.
Anisotropic Scattering Rates
The behavior of the self-energy £(k, !)impliesof
course corresponding anisotropy for the scattering
Fig. 23.38. Scattering rate
−1
(!) of optimally (a)andover-
doped (b) hole-doped cuprates versus frequency at the
nodal and antinodal point ofthe BZ and calculated for vari-
ous temperatures.The anisotropy results from coupling to
spin fluctuations and disappears in the overdoped case.
Thus, a crossover from a non-Fermi-liquid to a Fermi-
liquid behavior occurs. Note also the feedback effect of
superconductivity for different parts of the BZ at optimal
doping
rate of the quasiparticles and for the conductivity.
We discuss now the anisotropy of the scattering rate
−1
(!) of hole-doped cuprates at different points on
the Fermi surface.
In Fig. 23.38 we show our results for
−1
(!)at
the antinodal point and the nodal point,respectively,
for optimal doping (a) and for the overdoped case,
and (b) for various temperatures.In Fig.23.38(a) one
clearly sees that the scattering rate is very anisotropic
on the Fermi surface reflecting the anisotropy of the
coupling of elementary excitations to spin fluctua-
tions. In particular,
−1
(!)inthenormalstateisal-
1466 D. Manske,I. Eremin, and K.H.Bennemann
most three times larger at the antinodal point than
at the nodal point. This agrees with recent ARPES
experiments [123]. Furthermore, we find that for
! → 0,
Im £ ∝ ! .
This demonstrates non-Fermi-liquidbehavior in the
underdoped and optimally hole-doped cuprates.
In the overdoped cuprates the anisotropy between
nodal and antinodal points is strongly reduced and
disappears almost for ! → 0. Most importantly the
system then behaves more Fermi-liquid-like. Thelat-
ter is seen from Fig. 23.38(b), where one observes a
crossover from the Im £ ∝ ! to the Im £ ∝ !
2
be-
havior. This is also in agreement with experimental
observations [124]. Note, results shown in Fig. 23.38
suggest that for increasing doping the spectral den-
sity gets sharper around hot spots, while broader in
modal direction.This results from the F.G.-topology
and Q.
Below T
c
at the antinodal point
−1
(!) foroptimal
doped reveals a strong feedback at energies
! ∼ !
res
+
0
,
where !
res
refers to the resonant frequency of the
spin fluctuations (see Im ). This relation is due to
the simple fact that the self-energy £ is a convolu-
tion of the spin susceptibility
s
(peaked at !
sf
)and
the Green’s function of the dressed quasiparticles G
(peaked at
0
). Furthermore, note that the power law
for ! → 0changesto£ ∝ !
3
and that at the nodal
point the effect of superconductivity is rather weak
due to the node of the d
x
2
−y
2
-wave symmetry of the
superconducting order parameter.
In the overdoped cuprates below T
c
both at the
nodal and antinodal points no structure in the fre-
quency dependence of
−1
(!) occurs. The latter is
also clear, since spin fluctuations spectrum weak-
ens and does not reveal resonant condition below
T
c
. This is consistent with the behavior of
−1
(!)
above T
c
where crossover to Fermi-liquid behavior
takes place.
To summarize the doping dependence of the
quasiparticle scattering rate we find pronounced
non-Fermi-liquidbehavior in underdoped and opti-
mally doped cuprates (Im £ ∝ !) due to strong scat-
tering of quasiparticles by spin fluctuations. For all
Fig. 23.39. Calculated imaginary part of the self-energy
Im£(k
a
, !)attheantinodalwavevectork
a
and assuming
apseudogapE
g
=0.15t for various temperatures T =0.1,
0.05, and 0.03t in units of t
doping regions we find qualitatively agreement with
transport experiments on hole-doped cuprates (see,
for example, the discussion of Figs. 29–31 in [32]).
In particular, in the overdoped case the crossover
to Fermi-liquid-like behavior occurs (Im£ ∝ !
2
)
that reflects the weakening of the spin fluctuations
with increasing doping. In the superconducting state
the pronounced spin fluctuations reveal structure in
−1
(!) at the antinodal point of the Brillouin zone
for underdoped and optimally doped cuprates. Due
to weakening of spin fluctuations this structure dis-
appears with increase of doping towards overdoped
cuprates. Our results for Fermi-liquid versus non-
Fermi-liquid seem quite general and could be used
as a basis for systematic studies.
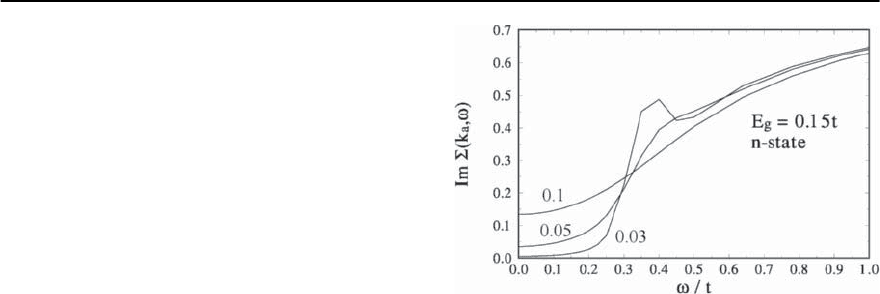
In order to illustrate the influence of the pseudo-
gap E
g
on the elementary excitations we have calcu-
lated the self-energy including in the energetic dis-
persion the pseudogap E
g
(k)=E
g
(cos k
x
−cosk
y
)
(T
∗
=0.1t = 250 K).
In Fig. 23.39 we show the evolution of the imagi-
nary part of the self-energy Im£(k
a
, !) for decreas-
ing temperature at the antinodal point of the BZ
where the pseudogap is maximal. In the pseudogap
regime the self-energy shows a gap-like feature up to
2E
g
. The renormalization of the quasiparticle scat-
tering rate leads to the peak at 3E
g
and it becomes
more pronounced for decreasing temperature. Cor-
respondingly this peak in the imaginary part of the
self energy at 3E
g
reveals an enhancement of the Re£.

23 Electronic Theory for Superconductivity 1467
As a result the quasiparticle effective mass m
∗
en-
hances in comparison to its value at ! =0.Our
results are in qualitative agreement with complex
optical conductivity results on underdoped Bi2212,
YBCO, and LSCO compounds [125].
23.4.3 Dynamical Spin Suscep tibility
An important quantity in our model is the dynam-
ical spin susceptibility, which is calculated in the
random-phase-approximation (RPA) for renormal-
ized Green’s functions, as discussed in the previous
section. Concerning the validity of the results ob-
tained by the model hamiltonian (see (23.6) and
(23.7)) one should remember that physically the
magnetic activity in the CuO
2
-planes results from
the Cu-spins (and the spin polarizations induced by
them into the p-band). The behaviour of the Cu-
magnetic momentsin the T–x plane (phase diagram)
need to be studied directly. One of the most impor-
tantquestionsishowthespinexcitationspectrum
changesupondopinginhigh-T
c
cuprates.Due to the
nesting properties of the Fermi surface at the wave
vector Q both electron and hole-doped cupratesshow
an enhancement of the spin response at the antifer-
romagnetic wave vector, which is further augmented
by the RPA denominator. These antiferromagnetic
fluctuations induced by the itinerant carriers can be
characterized by the frequency !
sf
of the spin fluctu-
ations where !
sf
refers roughly to the peak position
in the dynamical spin susceptibility.
In Fig. 23.21 we show the results of our calcu-
lations for Im(Q, !) versus frequency at differ-
ent doping concentration. As one sees in the under-
doped cuprates Im shows a sharp peak and fol-
lows an Ornstein–Zernicke behavior. The position
of the peak defines the spin fluctuation frequency
!
sf
.With increasing doping !
sf
shifts towards larger
frequencies and the peak becomes less pronounced.
This agrees well with experimental data of INS. This
behavior is expected,since for increasing doping the
system goes away from the antiferromagnetic insta-
bility and therefore !
sf
becomes larger. This, for ex-
ample, indicates that in the overdoped regime the
renormalization of the elementary excitations will be
isotropic at different parts of the Fermi surface,while
Fig. 23.40. Momentum dependence of the real part of
the spin susceptibility for the optimally electron-doped
cuprates Re(q, !) along the Brillouin zone route (0, 0) →
(, 0) → (, ) → (0, 0) at U /t =4,T = 100 K and
! =0(solid curve)and! = !
sf
=0.47t (dashed curve).
The main contributions to the Cooper-pairing interaction
come from the wave vectors q
pair
and Q
pair
in optimally and underdoped materials the strongest
scattering takes place at the parts of the Fermi sur-
face that are connected by the wave vector (, )
(so-called “hot spots”). These results are consistent
with the behavior of the elementary excitations that
we have discussed previously.
What is the spin spectrum of the electron-doped
cuprates? As expected the electron-doped cuprates
demonstrate also the presence of the antiferromag-
netic fluctuationsatQ.Thisis seen in Fig.23.40where
we plotthe behavior of the Re(q, !) along the route
(0, 0) → (, 0) → (, ) → (0, 0) of the first BZ at
! =0and! = !
sf
.InbothcasesRe yields a peak
at wave vector Q. However, this peak is much weaker
than in hole-doped cuprates due to the weaker nest-
ing properties of the corresponding Fermi surface.
The latter can be seen by analyzing the position of
the!
sf
in the electron-doped cuprates.While in hole-
doped cuprates at optimal doping it is of the order of
!
h
sf
≈ 20 meV,
in the electron-doped cuprates it is approximately
!
e
sf
≈ 60 meV.
Therefore, the effect of the spin fluctuations on the
elementary excitations will be weak in the electron-
doped cuprates. For example, since the energy scale

1468 D. Manske,I. Eremin, and K.H.Bennemann
of the spin fluctuations is large, the low-energy
properties in the electron-doped case will behave
more like in the standard Fermi-liquid theory (i.e.
£
∼ !
2
). This is suggested experimentally by the
quadratic temperature dependence of the electronic
part of the resistivity in electron-doped cuprates.
Another important feature is that electron-doped
cuprates will behave more like overdoped cuprates,
since their spin dynamics is very similar. A conse-
quence is the absence of the “kink” feature and “hot
spots”in the electron-doped cuprates.
23.4.4 Order Parameter: Doping Dependence
Let us now discuss the superconducting properties of
the cuprates. The most important question concerns
the symmetry of the superconducting order param-
eter and its doping dependence in hole-doped and
electron-doped cuprates. Due to the repulsive nature
of the spin fluctuation mediated pairing interaction
a conventional isotropic s-wave pairing is not possi-
ble. Therefore, for singlet pairing the orbital state of
the Cooper-pair wave function should be the l =2
representation that corresponds to a d-symmetry of
the order parameter. The particular symmetries that
mightoccur in the CuO
2
planearetheonesbelonging
to the corresponding tetragonal crystal field symme-
try D
4h
. The corresponding representations can be
substituted into the gap equation and the symmetry
that yields the eigenvalue = 1 at highest tempera-
ture is the realized symmetry of the superconducting
order parameter in layered cuprates.
The solutions of the generalized Eliashberg equa-
tions within the FLEX approximation give the d
x
2
−y
2
-
wave symmetry of the superconducting order pa-
rameter in the CuO
2
-plane for both hole and electron
doping as shown for demonstration in Fig. 23.41(a)
for the electron-doped cuprates at optimal doping.
This is easy to understand if one remembers that the
main contributionto thepairing comesfrom thespin
susceptibility that is peaked at Q≈ (, ). The latter
connects in the hole-doped cuprates the parts of the
Fermi surface close to the M pointsof theBZ.Keeping
in mind the repulsive nature of the pairing interac-
tion one sees that in order to have a Cooper-pairing
the order parameter has to have different sign at the
Fig. 23.41. (a) Calculated d
x
2
−y
2 -wave superconducting gap
at T =0.8 T
c
and x =0.15 in the first square of the BZ. (b)
Calculated Fermi surface for the optimally electron-doped
cuprates. The +(-) signs and dashed lines refer to the signs
of the momentum dependence d
x
2
−y
2 -wave superconduct-
ing gap (k, ! = 0) and its nodes, respectively
corresponding parts of the Fermi surface connected
by the antiferromagnetic wave vector Q.Then,d
x
2
−y
2
-
wave symmetry is the most natural solution.
Since the topology of the Fermi surface does not
change significantly in the hole-doped cuprates at
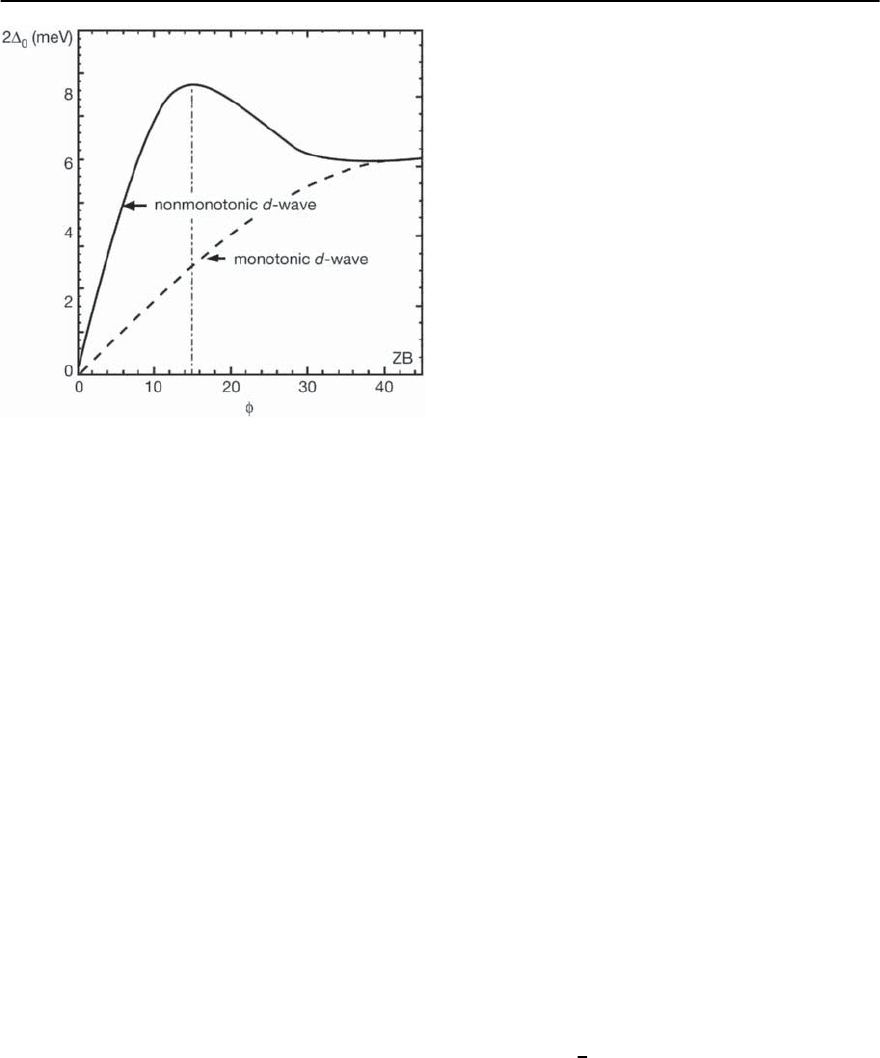
23 Electronic Theory for Superconductivity 1469
Fig. 23.42. Illustration of the non-monotonic d-wave be-
havior of the superconducting gap below T
c
at T =5K
in optimally electron-doped cuprates (x =0.15) along the
Fermi surface (the superconducting gap
0
changes from
the diagonal of the BZ towards the zone boundary(ZB) as
afunctionofangle [126]
least in optimally and overdoped cuprates the d
x
2
−y
2
-
wave symmetry is always the most prominent so-
lution of the gap equation. The situation is differ-
ent in the electron-doped cuprates where phonons
are more important and weaker nesting is present.
Assuming an exchange of antiferromagnetic spin
fluctuations as responsible for Cooper-pairing in
electron-doped cuprates we also obtain a d
x
2
−y
2
-wave
symmetry of the underlying order parameter for the
electron-doped cuprates at optimal doping.However,
as we pointedout earlier,thetopology of theelectron-
doped cuprates is such that the parts of the Fermi
surface connected by the Q are closer to the diag-
onals of the BZ rather than to M points as shown
in Fig. 23.41(b). Therefore, even though the symme-
try of the superconducting order parameter is still
d
x
2
−y
2
, the gap structure has some additional fea-
tures (higher harmonics, see Fig. 23.42) that reflect
the structure of the susceptibility and the corre-
sponding topology of the Fermi surface.
Hence, it is possible that the symmetry of the
superconducting order parameter can change with
doping. This in particular may be the case for the
overdoped compounds where the nesting becomes
weaker. In addition, if the electron–phonon coupling
playsa role it may overcomethe repulsive interaction
due to spin fluctuations and favor s-wave pairing.
In principle, it could happen that the gap symmetry
changes from d
x
2
−y
2
-wave to the s-wave for T
c
→ 0,
since more Cooper-pair condensation energy may
result in nodeless s-wave symmetry.
It is interesting to mention that phonons may also
assist in principle the d-wavepairingifoneassumes
that the important phonon mode participating in
the superconductivity is peaked at q ≈ (0.4, 0),
as shown in Fig. 23.41(b). Indeed, the parts of the
Fermi surface connected by the wave vector q have
thesamesignevenforthed
x
2
−y
2
-wavepairing.There-
fore,an attractiveelectron–phonon interaction could
contribute to d-wave pairing [122,127].
23.4.5 Resonance Peak and Magnetic Coherence
An important consequence of the spin-fluctuation-
mediated Cooper-pairing and d
x
2
−y
2
-wave symme-
try of the superconducting order parameter is the
peculiar behavior of the spin dynamics in the super-
conducting state. The feedback of superconductivity
on occurs due to the fact that the spin fluctuation
frequency !
sf
isofthesameorderasthesupercon-
ducting gap
0
, at least in the hole-doped cuprates.
One expects that the feedback effect of supercon-
ductivity on the spin excitations will be important if
the quasiparticles condensing into Cooper-pairs are
also partly involvedin the spin fluctuationdynamics.
Thus, it is important to see whether the experimen-
tally observed “resonance” peak and “magnetic co-
herence” effect for (q, !) can be explained within
our self-consistent electronic theory.
Let us start our study with the analysis of theimag-
inary part of the bare BCS-like expression for the spin
susceptibility(see (23.41)) for the d
x
2
−y
2
-wave case at
the wave vector Q=(, ); see Eq. (23.42):
Im
0
(Q, !)=
1
2
k
1−f
(
E
k
)
ı(! +2E
k
)
+
f
(
E
k
)
−1
ı(! −2E
k
)
. (23.132)
1470 D. Manske,I. Eremin, and K.H.Bennemann
Here, f
(
E
k
)
denotes the Fermi function and E
k
=
2
k
+
2
k
is the dispersion of the Cooper-pairs in the
superconducting state. As one can see from (23.132)
the imaginary part of the BCS spin susceptibility
has an important characteristic frequency !
DOS
that
arises from the density of states of the quasiparti-
cles in the superconducting state which have a gap in
their spectrum due to superconductivity. Note that
!
DOS
≈ 2(x, T). In order to describe the effect of
spin fluctuations one uses in the simplest case the
RPA spin susceptibility. Then, in addition to !
DOS
a
second characteristic frequency occurs in the RPA
spin susceptibility. In particular, one finds that the
structure in Im(Q, !) can also be determined by
the condition
1=URe
0
(Q, ! = !
res
)and
Im
0
(! = !
res
)=0,
see =
0
(1 − U
0
)
−1
and
=
0
([1 − U
0
]
2
+
[U
0
]
2
)
−1
.Therefore,with increasing U one sees that
the peak resulting from !
DOS
will shift to lower ener-
gies and most importantly will become resonant for
U = U
cr
. Note that this signals the occurrence of a
spin density wave collective mode.
In Fig. 23.43(a) we present our weak coupling re-
sults for different values of U for Im(Q, !)(i.e.
without taking into account the lifetime effects). In
the superconducting state Im becomes gaped ap-
proximately at 2
0
. With increasing U the peak in
Im shifts to lower frequencies and at U
cr
=4t it be-
comes resonant. Therefore, the resonance peak ob-
served in INS results in our model due to occurrence
of superconductivity,butis renormalized by the nor-
mal state spin excitations.
Another interesting feature at optimal doping re-
lates to the momentum dependence of Im(q, !)as
observed in LSCO.In contrast to some other cuprates
the susceptibility is peaked at the incommensurate
wave vector Q
i
=( ±ı, ±ı).In the superconduct-
ing state these incommensurate peaks behave rather
unusually. With decreasing frequency they first be-
come much more pronounced in comparison to the
normal state and at low enough frequency they dis-
appear [128,129]. This phenomenon was originally
called “magnetic coherence” due to the similarity
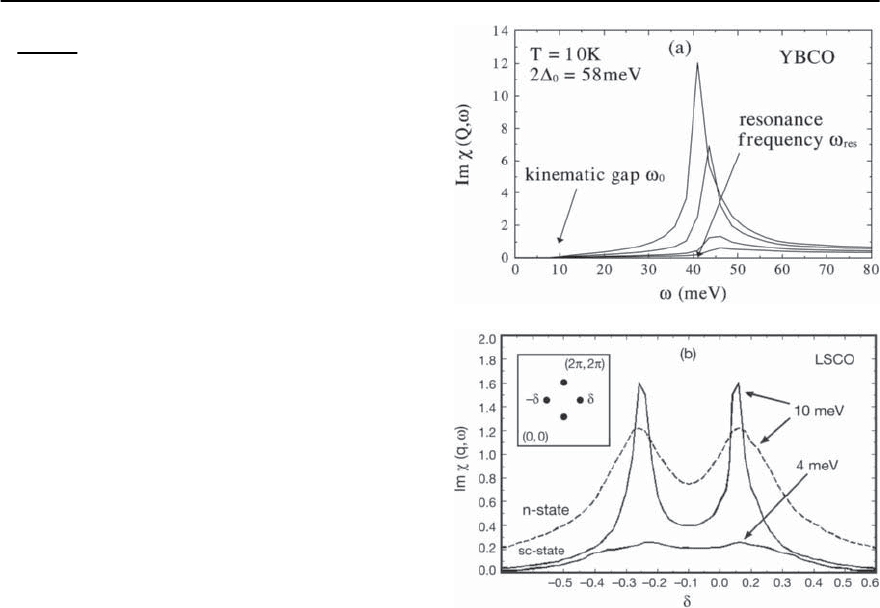
Fig. 23.43. Numerical results for the resonance peak and
magnetic coherence in the weak-coupling limit.(a)Imagi-
narypartof theRPAspinsusceptibilityinunits of states/eV
versus ! in the superconducting state at wave vector
Q=(, )forU/t=1,2,3, and 4 from bottom to top.Wefind
!
res
=41 meV. Below the kinematic gap !
0
,Im(Q, !)is
zero. (b) Calculated magnetic coherence: the solid curves
correspond to the superconducting state whereas the dot-
ted curve is calculated in the normal state. The observed
four peaks occur at Q
i
=(1±ı, 1 ±ı) (see inset)andin
the figure we show only the peaks at Q
i
=(1, 1 ± ı).In
our calculations we find for the parameter of incommen-
surability ı =0.18
of the observed effect with the quasiparticle coher-
ence peak that occurs below T
c
in conventional su-
perconductors. Using the parameters of the tight-
binding dispersion for LSCO we found the same be-
havior of Im in our calculations [130],as shown in
Fig. 23.43(b).
Thesameisthecasefortheresonancepeak.One
sees that in LSCO !
sf
is comparable to the supercon-
ducting gapand therefore,there is a strong renormal-
23 Electronic Theory for Superconductivity 1471
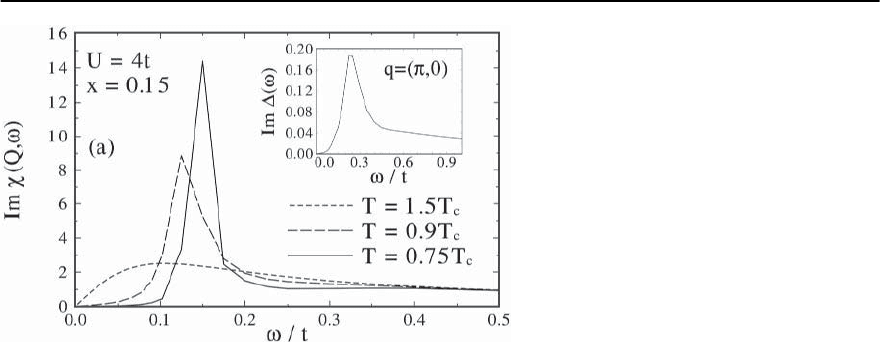
Fig. 23.44. Resonance peak: Imaginary part of
the RPA spin susceptibility at Q =( , )cal-
culated using the FLEX approximation.For the
normal state we get !
sf
=0.1t and in the su-
perconducting state we obtain !
res
=0.15t.
Assuming t = 250 meV we find that 0.16t =
40 meV. Inset: Imaginary part of the gap func-
tion at T =0.75T
c
for wave vector =(, 0)
ization of the spin spectrum in the superconducting
gap. Due to the reduced scattering below T
c
the in-
commensurate peaks at Q
i
become sharper than in
the normal state.Furthermore,for decreasing energy
the intensity of the peaks will decrease due to a su-
perconducting gap. At energies of about 2 meV we
do not obtain any well-resolved peaks. This is shown
in Fig. 23.43(b).
Using the self-consistent FLEX approach we see
that our weak-coupling results do not change drasti-
cally. Many experimental facts can be already under-
stood on the basis of the d
x
2
−y
2
-wave symmetry of the
superconducting order parameter. However, in the
strong-coupling Eliashberg approach the spin exci-
tation spectrum can be studied self-consistently. For
example, in Fig. 23.44 we show the FLEX results for
Im(Q, !) in the normal and superconducting state.
In the normal state the spin fluctuation spectrum
shows a peak at !
sf
=0.1t. In the superconduct-
ing state the resonance peak occurs at !
res
=41 meV
and remarkably already at T =0.7
c
the resonance
peak is fully developed and does further not change
its position in frequency with lowering temperature.
This reflects that in the strong-coupling Eliashberg
approach the superconducting gap evolves rapidly
below T
c
and reaches almost its maximum already at
T =0.7T
c
.
Physically speaking, the resonance peak results
from the frequency dependence of the supercon-
ducting gap function, which is calculated self-
consistently,and from the vicinity to a spin-density-
wave collective mode that satisfies (23.43).Since the
quasiparticle scattering rate is reduced in the super-
conducting state the strong and weak-coupling re-
sults do not differ drastically.
In Fig. 23.45 we show results (see I. Eremin et
al. [131]) for the resonance at incommensurate mo-
mentum. Note that in particular the structure near
q (, ) for 0.8 and 1.2. RPA results give
that this structure has maximal intensity along the
BZ diagonal directions.
The spin-susceptibility in bilayered cuprates will
also exhibit resonance peaks for the odd and even
parts of at T < T
c
((q, !)=
e
(q, !)cos
2
(q
z
d/2) +
0
(q, !)sin
2
(q
z
d/2)). The resonances of
e
and
0
occurat differentfrequenciesdueto J
⊥
and
hopping t
⊥
(Note that t
⊥
causes two Fermi-surfaces
representing bonding and antibonding states). For
underdoped cuprates the resonance frequency !
e
res
increases, while !
0
res
decreases for decreasing dop-
ing.
It is of general interest to study the doping de-
pendence (in particular for monolayered cuprates)
of the resonance peak in the overdoped and under-
doped cuprates. In Fig. 23.46 we show our results
for the doping dependence of !
res
from underdoped
to the overdoped regimes. Note that !
res
decreases
away from optimal doping. In the overdoped regime
the resonance peak is mainly determined by the su-
perconducting gap, since the spin fluctuations get
weaker and play a less significantrole. The supercon-
ducting gap decreases in the overdoped cuprates and
