Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.


1432 D. Manske,I. Eremin, and K.H.Bennemann
Fig. 23.18. RPA diagrams for the effective pairing interaction V
eff
for singlet pairing in cuprates resulting from the exchange
of longitudinal and transverse spin and charge fluctuations. The solid lines refer to the one-particle Green’s function that
are taken in accordance with (23.15) and (23.17) and the dashed lines denote an effective Coulomb interaction
˜
U.The
first diagram leads to a renormalized chemical potential. The diagrams refer to Cooper-pairing due to spin fluctuations.
Note that for singlet pairing only an even number of bubble diagrams occur due to Pauli’s principle describing both spin
and charge fluctuations. The charge and spin fluctuations can be separated from each other and give rise to the first and
second terms in (23.21)–(23.22), respectively. Note that the selection of diagrams requires an approximation: we solve
the particle–particle (i.e.the Cooper) channel assuming that V
eff
is only particle-hole-like.A comprehensive study would
require solving in addition the particle-hole channel for the magnetic instability using all particle–particle contributions
for V
eff
. This would yield the set of Parquet-equations (if further mode–mode coupling is taken into account)
Obviously, the effective pairing interaction de-
fined in Fig. 23.18 is related to the self-energy £
shown in Fig. 23.13 and thus to (23.17) by V
eff
=
ı£/ıG.A similar relation holds for the vertex correc-
tions leading to
˜
U →
˜
U
eff
. To a good approximation
they have a weak !-dependence, and therefore do
not change the dynamics of the elementary excita-
tions and the spectrum of the superconducting gap
too much. Note also that in general the Green’s func-
tions used for V
eff
may be different from those of the
carriers that participate in Cooper-pairing. Further-
more,also the form and value of the bare susceptibili-
ties may differ for localized anditinerant magnetism.
As mentioned above, the matrix Green’s function
ˆ
G(k) and the self-energy are related by the Dyson
equation (23.15):
ˆ
G
−1
=
G
−1
0
− £
G
−£
F
−
¯
£
F
¯
G
−1
0
−
¯
£
G
, (23.20)
where £
G
and £
F
denote the normal and anomalous
part of the self-energy, respectively. Using the dia-
grams displayed in Fig. 23.18 and employing Mat-
subara frequencies the self-energies are given by
£
G
(k, ı!
n
)=
1
ˇN
k
i!
n
1
2
˜
U
eff
˜
U
×
c0
(q, i
m
)
1+
˜
U
c0
(q, i
m
)
+
3
2
˜
U
eff
˜
U
s0
(q, i
m
)
1−
˜
U
s0
(q, i
m
)
+
˜
U
eff
˜
U
G
(q, i
m
)
G(k
, i!
n
) (23.21)
and
£
F
(k, ı!
n
)=−
1
ˇN
k
i!
n
1
2
˜
U
eff
˜
U
×
c0
(q, i
m
)
1+
˜
U
c0
(q, i
m
)
−
3
2
˜
U
eff
˜
U
s0
(q, i
m
)
1−
˜
U
s0
(q, i
m
)
−
˜
U
eff
˜
U
F
(q, i
m
)
G(k
, i!
n
) , (23.22)
wherei
m
= i!
n
−i!
n
.Thefirst and secondterms re-
fer to charge and spin fluctuations,respectively.Note,
the bare susceptibilities can be defined in terms of
G,F
,i.e.
c0
=
G
−
F
and
s0
=
G
+
F
.Both
are defined in Appendix A. The term
˜
U
eff
˜
U
G,F
on
the right-hand side compensates for double count-
ing that occurs in the second order.
So far, the Eliashberg-like equations have been
derived on the imaginary axis and for finite tem-

23 Electronic Theory for Superconductivity 1433
peratures ˇ
−1
= k
B
T.Thisisconvenientbecauseof
the spectral properties of the corresponding Green’s
function. However, in order to compare directly with
experiment we need the solution of the self-energy
equations on the real !-axis. One possibility would
be to solve the generalized Eliashberg equations
slightly above the real axis [70]. However, we fur-
ther want to avoid continuation to the real !-axis,
z = i!
n
→ ! + i0
+
, after a solution has been
obtained. This can lead to numerical uncertainties
and instabilities. Therefore, we formulate the gener-
alized Eliashberg equations from the beginning di-
rectly on the real frequency axis. To do this we use
spectral representation of the one-particle Green’s
functions [71,72]. Although this requires a large nu-
merical effort, it is not at all a problem with today’s
computer power. Details of the calculation are given
in Appendix A. After performing the sum over the
Matsubara frequencies [73] we arrive at the follow-
ing set of equations for the quasiparticle self-energy
components £
( = 0, 3, 1) with respect to the Pauli
matrices
in the Nambu representation:
£
(k, !)=N
−1
k
∞
0
d§
P
s
(k − k
, §)
+(ı
0
+ ı
3
− ı
1
) P
c
(k − k
, §)
×
∞
−∞
d!
I(!, §, !
)A
(k
, !
) . (23.23)
P
s
and P
c
refer to spin and charge fluctuations, re-
spectively.The kernel I and the spectral functions A
are given by
I(!, §, !
)=
f (−!
)+b(§)
! + i ı − § − !
+
f (!
)+b(§)
! + iı + § − !
(23.24)
and
A
(k, !)=−
−1
Im
[
a
(k, !)/D(k, !)
]
. (23.25)
The denominator is given by
D =
[
!Z
]
2
−
(k)+
2
−
2
,
Also we use a
0
= !Z, a
3
= (k)+,anda
1
= Z.In
(23.24),f and b denote the Fermi and Bose distribu-
tion function, respectively.
The band filling
n =1/N
k
n
k
is determined with the help of the k-dependent oc-
cupation number
n
k
=2
∞
−∞
d!f (!)[A
0
(k, !)+A
3
(k, !)] ,
which is calculated self-consistently. Note that this
introduces the doping dependence of the supercon-
ducting gap, the elementary excitations and spin ex-
citations. The case n = 1 corresponds to the half-
filling. The interaction between quasiparticles due
to spin and charge fluctuation is given by
P
s
=(2)
−1
˜
U
eff
˜
U Im(3
s
−
s0
) ,
P
c
=(2)
−1
˜
U
eff
˜
U Im(3
c
−
c0
) . (23.26)
So far our formulation has been quite general and
applies similarly to any system with strong interac-
tion of the carriers with spin fluctuations.In case of
strong hybridizationbetween the Cu d-states and the
oxygen p-states one may approximately use the same
Green’s functions for determining G(k, !), £(q, !),
and (q, !). In this effective one-band picture one
uses
˜
U = U .
10
Further neglection of vertex correc-
tions yields
˜
U
eff
=
˜
U = U.
From now on the local character of the Cu spins
(characterized by S
i
· ) and the hybridized states
resulting from d-electrons and p-electrons are incor-
porated into the one-band states with the effective
coupling U .Itremainstheonly parameter (in addi-
tion to a bare tight-binding band structure
k
), and
we will assume U 4t in most of the cases;
0
now
refers to the susceptibility of this band described by
(23.7) and (23.8). Then, the above expressions con-
stitute a system of coupled equations for the quasi-
particles Green’s function and Cooper-pairs. These
equations must be solved numerically by iterations
for a temperature given and fixed parameters t, U,
10
Note that
˜
U = U
eff
neglects differences between the itinerant carriers and the (local) Cu-spins.

1434 D. Manske,I. Eremin, and K.H.Bennemann
as well as doping x.
11
The spin susceptibility is the
important input for determining £ and G. In general,
one expects that (q, !)isapproximatelygivenby
RPA theory, with
s0
=−
1
2
T
k
Tr
G(k)
0
G(k + q)
0
(23.27)
and
c0
=−
1
2
T
k
Tr
G(k)
3
G(k + q)
3
. (23.28)
Here, Tr stands for the trace of the corresponding
2 × 2matrix.
In the case of electron-doped cuprates we may
safely assume that (q, !) results from the itiner-
ant quasiparticle states in the upper Hubbard band.
Thus, we have = {G} with
0
given by (23.27) and
(23.28).This yields a Berk–Schrieffer-type theory for
the coupling between electrons described by G and
the spin fluctuations described by
=
0
+ U
eff
0
. (23.29)
On the other hand, in the case of hole-doped
cupratesthe hybridizationbetween the p and d-states
suggests for simplicity that the spin excitations may
be determined (at least approximately) by effective
quasiparticle states described by G(k, !). Hence, we
use = {G} and for the RPA-form and for
0
again (23.27) and (23.28). This model is supported
by the observation of a strong feedback effect of G
on [41].
In the case of ruthenates the spin excitations de-
scribed by (q, !) result from the quasiparticles of
the ˛, ˇ,and -states. Hence, the Green’s function G
is also used for calculating the spin susceptibility, i.e.
= {G}.
Summary
In summary, we use for the cuprates and ruthenates
a Berk–Schrieffer-type theory for the behavior of the
quasiparticles coupling to spin excitations:
G = G{}, = {G}, (23.30)
and determine from an electronic theory within
RPA. Obviously, the calculation demands a high de-
gree of self-consistency for determining G,theresul-
tant elementary excitations, the spin susceptibility,
and for superconductivity.Details of this procedure
are given in Appendix B.
The dynamical spin susceptibility
s
determines
the properties of the electronic system.Itspeak struc-
ture at Q
AF
=(, ) is important. The latter arises
due to the nesting properties of the Fermi surface.
The RPA denominator enhances further this peak
structure of the spin susceptibility.The charge fluc-
tuations arise also from the nesting properties, but
are not that much enhanced by the RPA denomina-
tor. Therefore, the charge fluctuations play a smaller
role for Cooper-pairing. However, some other inter-
actions (like electron–phonon interaction or long-
range Coulomb repulsion) may change the situation
completely and may lead to the enhancement of the
dynamical charge susceptibility. Thismay happen at
lowdoping wherethescreening is smallerand the lat-
tice distortions can be more important.Although we
do not consider these effects explicitly in our elec-
tronic theory one can incorporate them relatively
easily in our Eliashberg-like theory by just changing
mainly the form of
c
.
23.2.3 Elementary Excitations
For understanding the high-T
c
cuprates their ele-
mentary excitations are of central significance.First
we discuss those in hole-doped cuprates. Using the
Green’s functions for the elementary excitations (i.e.
the local density of states) one gets after continuation
to the real !-axis and for a fixed temperature for the
spectral density
11
Note that one has to use the solution of the generalized Eliashberg equations in order to solve the corresponding
two-particle vertex equations. This yields vertex corrections and thus a renormalized Coulomb interaction U → U
eff
.
In [57] it is argued that vertex corrections are, to a good approximation, frequency independent, and therefore the
dynamics of the coupling of elementary excitations and spin excitations remain unchanged. In view of our calculations
this seems to be in good agreement with experiments.
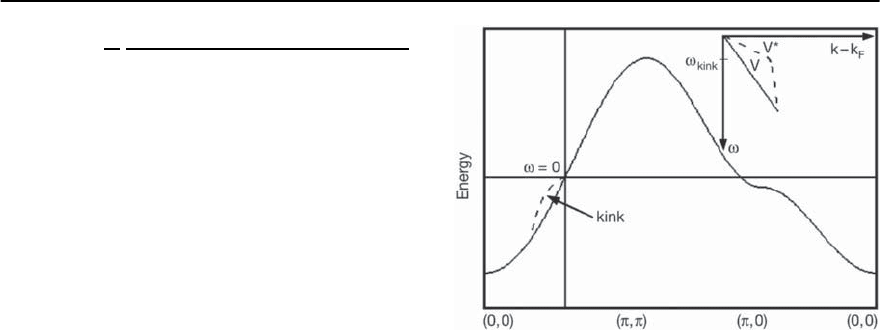
23 Electronic Theory for Superconductivity 1435
A(k, !)=−
1
£
(k, !)
[
! −
k
− £
(k, !)
]
2
+
[
£
(k, !)
]
2
.
(23.31)
Here,
k
is the bare energy dispersion given by (23.8)
and £
(k, !)and£
(k, !) are the real and imaginary
parts of the self-energy, respectively. The renormal-
ized energy dispersion !
k
of the quasiparticles is
given by
!
k
=
k
+Re£(k, ! = !
k
) . (23.32)
Here, the doping dependence occurs due to a change
in the chemical potential of
k
and in particular from
the frequency dependence and also from the dop-
ing dependence of the dynamical spin susceptibility
(q, !).
In Fig. 23.19 we demonstrate the importance of
many-body effects due to the self-energy. The renor-
malization of the dispersion by £ causes structure in
the dispersion, the so-called kink feature. We show
the unrenormalized tight-binding energy dispersion
k
in the normal state along the route (0, 0) →
(, 0) → (, ) → (0, 0) of the first BZ. Below the
Fermi level the measured energy dispersion !
k
along
(0, 0) → (, ) changes compared to the bare tight-
binding case due to the self-energy corrections. We
define the kink at the inflection point of the dashed
curve where the renormalized dispersion tends to
approach again the bare dispersion
k
. Note that the
renormalization of
k
is expected to be anisotropic.
Recent studies by Dessau and co-workers [74] re-
vealed no kink structure along (, 0) → (, )di-
rection in the normal state, but only in the supercon-
ducting state.
The self-energy £(k, !) for cuprates is calculated
self-consistently using the 2D one-band Hubbard
Hamiltonian for the CuO
2
-planes and assuming cou-
pling of the quasiparticles to spin fluctuations. The
superconducting gap function (k, !)isalsocalcu-
lated self-consistently. As described earlier the full
momentum and frequency dependence of the quan-
tities iskept.No further parameter is introduced.Itis
important to realize that due to the combined effects
of Fermi surface topologyand(q = Q, !)atthean-
tiferromagnetic wave-vector Q
AF
=(, ), the k and
! dependence of £(k, !) become very pronounced
and change the dispersion !(k).
Fig. 23.19. Calculated bare tight-binding energy dispersion
for hole-doped cuprates in the normal state using (23.8).
The dashed curve illustrates the changes due to renormal-
ization, !
k
=
k
+Re£(k, ! = !
k
). Due to the structure
in Re£ the energy dispersion shows a kink feature along
the (0, 0) → ( , ) and also other directions in the first
Brillouin zone.The inset shows an enlargement of the kink
structure. The maximum deviation from the bare disper-
sion and also the renormalized velocity of the quasiparti-
cles v
∗
reflect the behavior of the self-energy and thus the
coupling to spin fluctuations (or in general also possibly to
phonons)
Most importantly, the changes in the electronic
dispersion are anisotropic in the first BZ. This is il-
lustrated in Fig. 23.20 where we show the Fermi sur-
face of optimally hole-doped cuprates. Due to the
fact that the spin susceptibility (q, !)hasstruc-
ture mainly at !
sf
and for the transferred wave vec-
tor q = Q the influence of (q, !) on the elementary
excitations is expected to be very anisotropic with re-
spect to the differentparts of the Brillouin Zone.First,
the antiferromagnetic wave vector Q =(, )con-
nects exactly quasiparticles at the Fermi level close
to the (0, ) points of the first Brillouin Zone. These
quasiparticles experience the strongest coupling to
antiferromagnetic spin fluctuations. Quasiparticles
at the diagonals of the BZ are not connected by the Q
and thus have smaller scattering by spin fluctuations
at the Fermi level. The corresponding point on the
Fermi surface is called a cold spot or a nodal point.
Furthermore, the quasiparticle states at the Fermi
level close to the M =(0, )pointinthefirstBZare
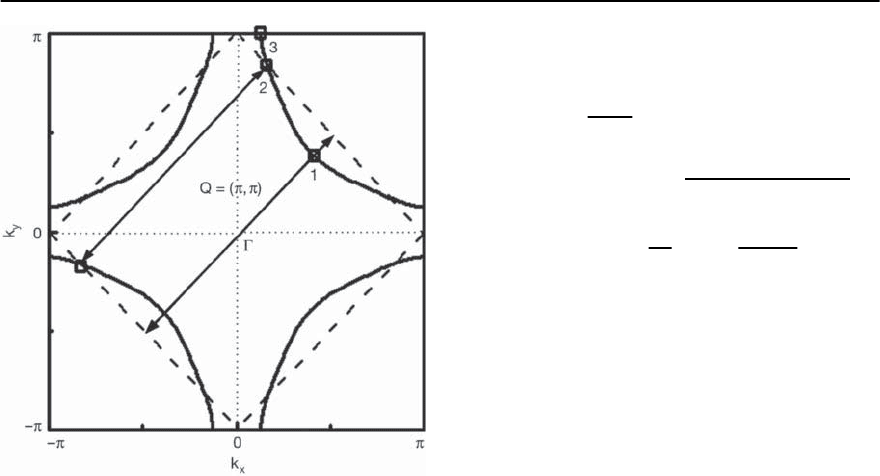
1436 D. Manske,I. Eremin, and K.H.Bennemann
Fig. 23.20. Illustration of the anisotropy of the elementary
excitations using the calculated Fermi surface for hole-
doped cuprates in the first Brillouin (BZ) zone for a single
CuO
2
-layer. The anisotropy can be characterized by three
different points on the Fermi surface.Point number 1 refers
to the diagonal part of the BZ (the so-called nodal point
or cold spot) and point number 3 refers to the so-called
antinodal point close to (0, ). The dashed line denotes
the magnetic BZ crossing the electronic Fermi surface ex-
actly at the “hot spots” (labeled number 2). The antifer-
romagnetic wave vector Q connects via scattering by spin
fluctuations the two pieces of the Fermi surface mainly at
the hot spots. At the (0, ) points and along the diagonals
thewavevectorQ connects quasiparticle states below the
Fermi level only. Note that the characteristic anisotropic
behavior of the elementary excitations may help to distin-
guish the resultant kink structure from the one which may
be caused by electron–phonon coupling
usually called antinodal points. Note that the quasi-
particle states at cold and hot spots connected by Q
lie close to the Fermi level. This will be important
later when discussing the kink feature. Therefore, we
may define three characteristic regions at the Fermi
surface regarding their sensitivity to coupling to an-
tiferromagnetic spin fluctuations (see Fig. 23.20).
Furthermore, this feature in £(k, !)changesthe
spectral density and the energy dispersion. Using
Fig. 23.13 the self-energy on the real axis within
the weak-coupling limit is approximately given by
(see Appendix C)
£(k, !) ≈ −
UU
eff
4
(23.33)
×
k
∞
0
d!
Im
RPA
(k − k
, !
)
! − !
−
k
×
coth
!
2T
−tanh
!
− !
2T
.
Due to the momentum and energy conservation one
expects a characteristic structure in £. In the follow-
ing we set U
eff
= U.
It is important to mention that the self-energy
has a strong frequency dependence, while the bare
energy dispersion of the carriers
k
has mostly no
frequency dependence. Thus, already in the normal
state, £(k, !) has a maximum reflecting a corre-
sponding maximum of Im at q ≈ Q and ! ≈ !
sf
.
Then, the kink position follows from the pole of the
denominator of (23.34). This leads to the “kink con-
dition”
!
kink
≈ E
k−Q
+ !
sf
(x) . (23.34)
This gives an estimate of the position of the kink.
We w i ll disc uss later h ow !
sf
depends on the doping
concentration.Notethatin theunderdopedregime of
hole-doped cuprates a normal-state pseudogap with
d
x
2
−y
2
-wave symmetry opens up below T
∗
around the
antinodal point (0, ).This leads to a smaller density
of states and therefore to a smaller coupling of holes
to spin fluctuations.Furthermore,ifthe pseudogap is
larger than the superconducting gap, no kink struc-
ture below T
c
should be present along the antinodal
direction.
What happens in the superconducting state? Be-
low T
c
the superconducting gap (k, !)opens
rapidly for decreasing temperature T and becomes
maximal in momentum space around the M point
reflecting the momentum dependence of the effec-
tive pairing interaction. Therefore, the occurrence
of a kink structure only below T
c
in the antinodal
direction is a direct fingerprint of the spin excita-
tion spectrum.Furthermore,as we will discuss below
Im (Q, !) in (23.34) peaks at the resonance fre-
quency !
res
(roughly at !
sf
+ ). Therefore, the kink

23 Electronic Theory for Superconductivity 1437
condition in the superconducting states is given by
!
kink
≈ E
k−Q
+ !
res
(x) . (23.35)
Obviously, !
sf
, (k, !), and thus !
res
depend on
the doping concentration x. Their behavior is inti-
mately connected to the doping dependence of the
dynamical spin susceptibility(q, !) as will be dis-
cussed below.
Finally, in order to compare the spectral density
of the elementary excitations directly with results
for the local density of states measured by angle-
resolved photoemission spectroscopy one also needs
information about the corresponding matrix ele-
ments that are anisotropic and are dependent on the
energy of the incident photon.In addition,R.Manzke
et al. pointed out that polarization-dependent pho-
toemission also reveals a fine structure in the low
energy excitation spectrum that complicatesthe line-
shape analysis of the data [75]. In particular, for
a single-layer high-T
c
superconductor at optimum
hole-doping two maxima dependent on the orienta-
tion of the polarization vector are found. Note that
if the tetragonal symmetry of the crystal is broken
by the occurrence of a charge-density wave, see re-
lated formation of stripes for example, polarization-
dependent effects are to be expected.
In underdoped cuprates we study the influence
of the pseudogap formation on the spin fluctuations
by assuming an additional (to a superconducting)
d-wave gap in the electronic excitations
E
g
(k)=E
g
(0)(cos k
x
−cosk
y
)/2 . (23.36)
Below the pseudogap temperature T
∗
the electronic
density of states at the Fermi level is reduced due
to the gap in the electronic dispersion. Since E
g
(k)
is strongly momentum-dependent, the “kink” struc-
ture in the dispersion will reveal some changes along
(0,0)→ (, 0) in the pseudogap regime. While the
origin of the pseudogap has not yet been clarified
experimentally, it is instructive to see how the phe-
nomenological form used in (23.36) affects the ele-
mentary excitations and the spin excitations.
23.2.4 Dynamical Spin Suscep tibility
One of the most important quantityof our electronic
theory is the dynamical spin susceptibility. Notethat
controls the corresponding Cooper-pairing, for ex-
ample.We have already discussed that we assume the
magnetic activity of the Cu-spins and of the O-atoms
may be described by the states of the UHB in the case
of electron doping and by the hybridized p and d-
statesof the one-band Hamiltonian in the case of hole
doping. (This leads to an effective coupling constant
U (see the discussion in connection with (23.26)–
(23.30).) Then, from the elementary excitations of
the quasiparticles we calculate the irreducible parts
of the lowest order (Lindhard) spin and charge sus-
ceptibility in the normal state
s0,c0
(q, !)=−
k
f (
k
)−f (
k+q
)
k
−
k+q
+ iı
. (23.37)
Again,f denotes the Fermi distributionfunctionand
k
is theenergy dispersion.Due to thenesting proper-
ties of the Fermi surface
s0
and
c0
(in the following
abbreviated as
0
) are mainly peaked at the antifer-
romagnetic wave vector Q =(, ). (Note that, in
general,
s0
and
c0
can be peaked at different wave
vectors depending on the additional interaction in-
cluded in a model.) Using the random phase approx-
imation (RPA) this will be further enhanced, since
RPA
(q, !)=
0
(q, !)
1−U
0
(q, !)
. (23.38)
Like already the Lindhard susceptibility also
RPA
may yield low-energy antiferromagnetic spin fluc-
tuations at a frequency ! = !
sf
. (Note that for holes
in the p-band U refers to their effective interaction.
Note that the doping dependence of is controlled
by the chemical potential via band filling.On general
groundsweexpectthatfordopingx → 0inpar-
ticular spin density excitations and charge density
excitations compete with each other.)
In order to compare our resultswith inelastic neu-
tron scattering (INS) experiments, we calculate the
imaginary part of
RPA
(Q, !):
Im
RPA
(Q, !) (23.39)
=
Im
0
(Q, !)
(1 − U Re
0
(Q, !))
2
+ U
2
(Im
0
(Q, !))
2
.
Note that due to the vicinity to an antiferromagnetic
instability,Im
RPA
is characterized approximately by
an Ornstein–Zernicke behavior [28]
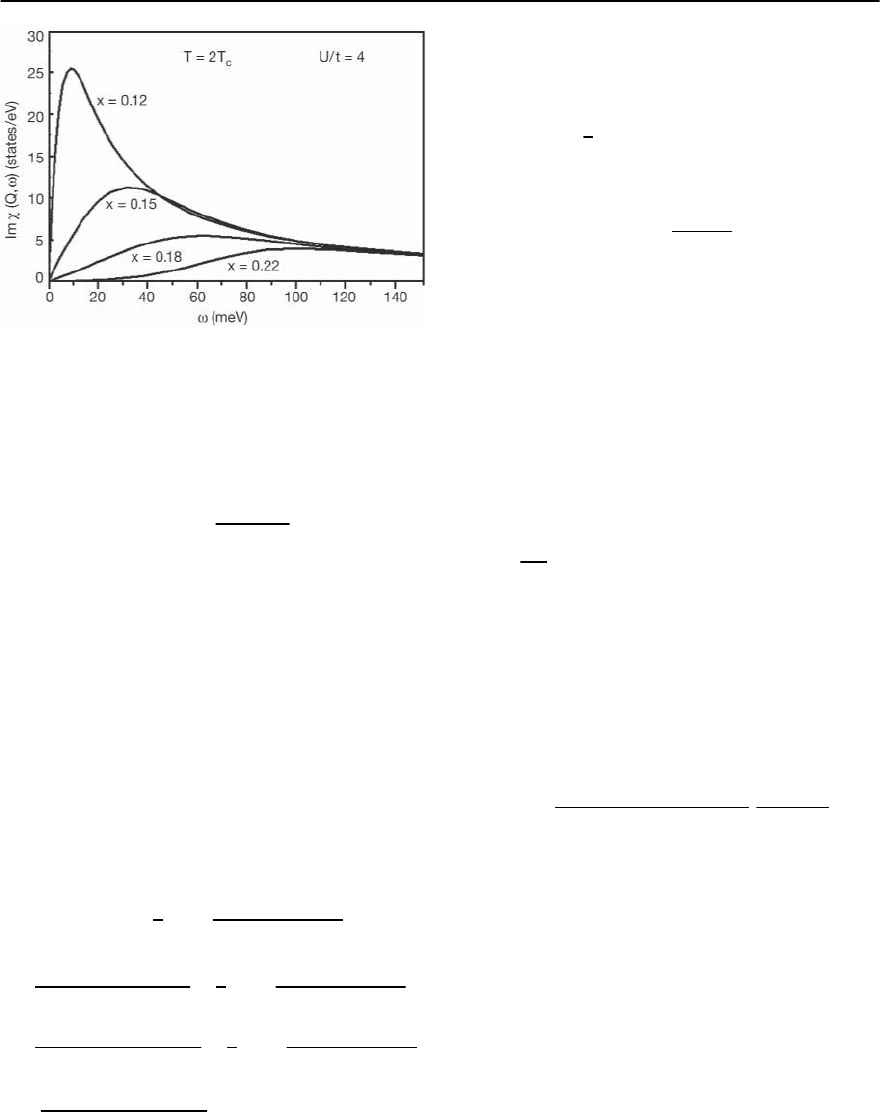
1438 D. Manske,I. Eremin, and K.H.Bennemann
Fig. 23.21. Dynamical spin susceptibility Im
RPA
(Q, !)
calculated using RPA and the generalized Eliashberg equa-
tions for hole-doped cuprates in the normal state at a
temperature T =2T
c
for various doping concentrations,
x =0.12 (underdoped), x =0.15 (optimal doping), and
x =0.18, x =0.22 (overdoped)
Im
RPA
(Q, !) ∝
!!
sf
!
2
+ !
2
sf
, (23.40)
with a pronounced peak at the wave vector q = Q and
! = !
sf
. In order to illustrate this in Fig. 23.21 we
show the doping dependence of Im
RPA
at the an-
tiferromagnetic wave vector Q versus frequency in
the normal state. Using t = 200 meV we find a typ-
ical value of !
sf
30 meV for the case of optimal
doping (x =0.15).
In the superconducting state the situation is dif-
ferent due to the presence of the superconducting
gap (k, !)=Z(k, !)(k, !). The essential behav-
ior follows already from the Lindhard susceptibility
0
. In the weak-coupling limit (Z ≡ 1)
0
is of BCS-
form [76]:
0
(q, !)=
k
1
2
1+
k
k+q
+
k
k+q
E
k
E
k+q
×
f
E
k+q
− f
(
E
k
)
! − E
k+q
+ E
k
+ iı
+
1
4
1−
k
k+q
+
k
k+q
E
k
E
k+q
×
1−f
E
k+q
− f
(
E
k
)
! + E
k+q
− E
k
+ iı
+
1
4
1−
k
k+q
+
k
k+q
E
k
E
k+q
×
f
E
k+q
+ f
(
E
k
)
−1
! − E
k+q
+ E
k
+ iı
2
. (23.41)
Thus,assuming d-wave symmetry (
k+Q
=−
k
)and
perfect nesting (
k+Q
=−
k
), the imaginary part at
the wave vector Q =(, )isgivenby
Im
0
(Q, !)=
1
2
k
1−f
(
E
k
)
ı(! +2E
k
)
+
f
(
E
k
)
−1
ı(! −2E
k
)
. (23.42)
Here, the energy E
k
=
2
k
+
2
k
is the dispersion
relation of the Cooper-pairs in the superconducting
state. Thus, for T =0and! > 0, the spin suscepti-
bility reveals a threshold at !
DOS
≈ 2
0
(x).
A closer inspection of (23.40) shows an interest-
ing resonant-like behavior of Im (q, !). Generally,
one finds that the structure of Im is determined by
Im
0
,if(URe
0
) = 1, and by (URe
0
) = 1, if this
can be fulfilled. Furthermore, one finds for increas-
ing U that the peak in Im shifts to lower energies.
Most importantly,
0
becomes resonant if the condi-
tion
1
U
cr
=Re
0
(q = Q, ! = !
res
) (23.43)
is satisfied. Note that this would signal the occur-
rence of a spin density wave collective mode with
energy !
res
. This resonance energy is slightly lower
than !
DOS
and the collective mode can be viewed as
a bound state inside the gap region 2(x, T).The real
part is given (at T =0)by:
Re
0
(Q, !
res
) (23.44)
=
k
E
k
E
k+Q
−
k
k+Q
−
k
k+Q
E
k
+ E
k+Q
2
− !
2
res
E
k
+ E
k+Q
2E
k
E
k+Q
.
Therefore,due to the feedback effect ofsuperconduc-
tivityon Im itsbehavior differs drastically fromthe
normal state and yields the formation of the reso-
nance feature at q = Q and ! = !
res
as it is observed
in INS experiments.
Physically speaking, the resonance peak appear-
ing in INS experiments only below T
c
is mainly de-
termined by the maximum of the superconducting
gap, but renormalized by normal state spin excita-
tions. Obviously,
0
and !
sf
are doping dependent
quantities. While in the overdoped case the renor-
malization due to !
sf
can be neglected, we find for a

23 Electronic Theory for Superconductivity 1439
too small
0
(i.e. the strongly underdoped case) that
the resonance conditionof (23.43) cannotbe fulfilled
and the nominator of (23.40) determines the peak
position. Thus, on general grounds one expects that
!
res
(x) ∝
1
!
sf
(x), underdoped cuprates
2
0
(x), overdoped cuprates
.
(23.45)
Note that the pseudogap will also affect the prop-
erties of the dynamical spin susceptibility below T
∗
.
For example,theuniform part of the spin susceptibil-
ity (q =0, ! = 0) which is proportional to the den-
sity of states will strongly decrease upon decreasing
temperature below T
∗
due to the gap in the electronic
spectrum.Later,wewilldiscuss in detailthe influence
of the pseudogap by using a new energy dispersion
k
=
(
0
k
)
2
+ E
g
(k)
2
. Similarly the spectrum of the
antiferromagnetic spin fluctuations Im(Q, !)will
show some structure at energies about 2E
g
(0) as fol-
lows from (23.42).Furthermore, the resonant condi-
tion, (23.43), can be fulfilled also below T
∗
, since the
pseudogap influences the spin fluctuation spectrum
as the superconducting gap below T
c
.
In the superconducting state the influence of the
pseudogap on the dynamical spin susceptibility is
expected to be small, since it is believed that both
are of d-wave type and that the superconducting gap
andpseudogap are similar in magnitude.In electron-
doped cuprates there seems to be no clear evidence
for a pseudogap behavior in the elementary excita-
tions and in the spin susceptibility below a certain
temperature T
∗
. Only recent tunneling experiments
on thin films show a pseudogap after a strong exter-
nal magnetic field ( H
c2
) has been applied [77].
23.2.5 Gap Equation: Singlet and Triplet
Cooper-Pairing
We want to investigate now in more detail how un-
conventional superconductivity can arise from the
exchange of spin fluctuations, from a purely elec-
tronic mechanism.
Singlet Cooper-Pairing
For this purpose let us first consider the simpli-
fied weak-coupling gap equation for singlet pairing
(T =0)
(k)=−
k
V
eff
s
(k − k
)
2E(k
)
(k
) , (23.46)
which is a self-consistency equation for the super-
conducting order parameter (k)inmomentum
space where k is defined in the first Brillouin zone.
V
eff
s
(k −k
)representstheeffectivetwo-particlepair-
ing interaction in the singlet pairing channel. This
is, to a good approximation, proportional to
RPA
if
Cooper-pairing due to spin fluctuations is present.
Again, the energy E(k)=
2
(k)+
2
(k)isthe
dispersion relation of the Bogolubov quasiparticles
where (k) denotes the bare electronic dispersion
of the electrons in the normal state. In contrast to
the pairing via electron–phonon coupling the mo-
mentum dependence cannot be neglected due to the
strong anisotropy of the pairing interaction. Note
that in the BCS theory V
eff
s
< 0(andV
eff
t
)istaken
as a constant. Therefore, one obtains a solution for
(k) of (23.46) which is structureless in momentum
space [50,76].
Let us now investigate how it is possible to solve
(23.46) with a repulsive pairing potential assuming
singlet pairing. Due to the fact that V
eff
s
> 0, one
would naively think that there exists no solution.
However, this is not so. If one takes into account
that V
eff
s
(k − k
) might have a strong momentum de-
pendence, it is easily seen that indeed the gap equa-
tion has a solution. This is illustrated in Fig. 23.22
whereweshowthefirstBrillouinzone(BZ)anda
Fermi surface that corresponds to the half-filled case
of the two-dimensional one-band Hubbard model.
This Fermi surface resembles the one measured in
the high-T
c
superconductor La
2−x
Sr
x
CuO
4
.Forsim-
plicity,we also assume an underlying tetragonal sym-
metry of the crystal.Thebehavior of a superconduct-
ing order parameter with d
x
2
−y
2
-wave symmetry and
resultant > 0and < 0 areas is indicated. If one
now assumes that the effective pairing interaction
V
eff
s
(k −k
) has a strong momentum dependence,for
example, a large peak at the antiferromagnetic wave
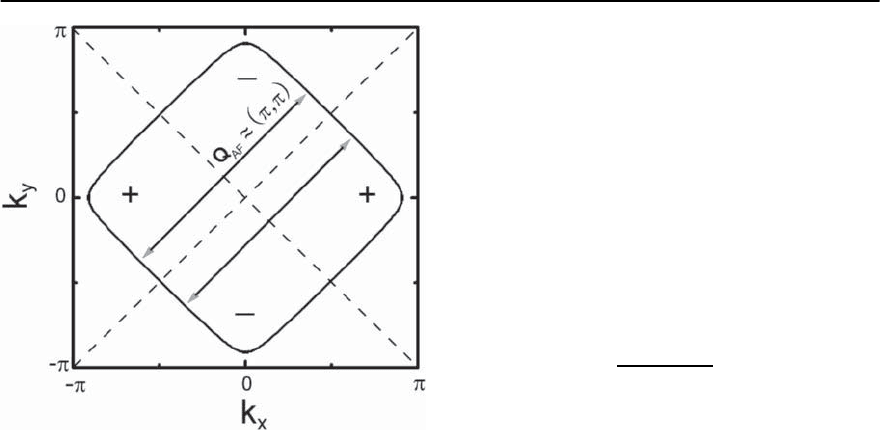
1440 D. Manske,I. Eremin, and K.H.Bennemann
Fig. 23.22. Illustration of the d
x
2
−y
2 -symmetry of the su-
perconducting order parameter in the first BZ of hole-
doped and electron-doped cuprates. The +(–) sign corre-
sponds to the sign of the order parameter. Two electrons
(holes) at the Fermi surface (solid curve) are coupled by the
exchange of antiferromagnetic spin fluctuations peaked
at ( , ) yielding the formation of Cooper-pairs only in
the case if the order parameter changes sign. The dashed
lines refer to the nodes in the d-wave order parameter
(k)=
0
[cos k
x
−cosk
y
]/2
vector q
AF
= Q =(, ) connecting different parts
of the Fermi surface, then the gap equation has a
solution for V
eff
s
> 0. Note that the wave vector Q
connects areas where is positive with those where
< 0. Thus, one indeed finds a solution of (23.46).
The simplest solution is the d
x
2
−y
2
-symmetry gap
(k)=
0
cos k
x
−cosk
y
/2 , (23.47)
which has nodes along the diagonals.Note,for an ef-
fective pairing interaction which is structureless in
momentum space such a solution of the gap equa-
tion for a d-wave order parameter would not be
possible. In fact an order parameter belonging to
an anisotropic s-wave representation (possibly with
nodes) would not satisfy the pairing condition men-
tioned above. In order to solve (23.46) for a pairing
interaction that is peaked at (, ) one definitely
needs an order parameter that changes sign. There-
fore, we see that the superconducting gap has less
symmetry than the underlying Fermi surface. In ad-
dition to a broken gauge invariance (U (1)) due to the
occurrence of superconductivitya further symmetry
is broken(in ourcasethe invariance under a rotation
of 90
◦
) we call this“unconventional”.Notice that this
neither implies an electronic pairing mechanism nor
a corresponding large value of T
c
, but a distinction
from electron–phonon pairing.
Triplet Cooper-Pairing
In the case of triplet Cooper-pairing one has to solve
the gap equation
(k)=+
k
V
eff
t
(k − k
)
2E(k
)
(k
) , (23.48)
where V
eff
t
(k − k
) denotes the effective two-particle
pairing interaction in the triplet pairing channel.
Most importantly, Pauli’s principle yields the plus
sign on the right-hand side of (23.48), which then
requires V
eff
t
< 0, i.e. an attractive pairing interac-
tion in momentum space. Note that this is similar to
pairing via electron–phonon interaction where the
minus sign in front of the right-hand side of (23.48)
is also canceled. A solution of the gap equation is
then relatively easy. In particular, if the transferred
momentum q = k − k
is small, one obtains p-wave
symmetry of the superconducting order parameter:
p
(k)=
0
(sin k
x
+ i sin k
y
) . (23.49)
Note that the condition q ≈ 0 is indeed fulfilled in
thecaseofsuperfluid
3
He that is close to a ferro-
magnetic transition. A similar situation is present
in Sr
2
RuO
4
(see its phase diagram in Fig. 23.10 in
which the -band forms a circle and has a high den-
sity of states). This already suggests triplet p-wave
symmetry for the order parameter of Sr
2
RuO
4
.Ob-
viously, the results for (q, !)incupratesexclude
triplet Cooper-pairing.
General Situation
Finally, let us critically mention that the arguments
given above for cuprates and ruthenates are weak-
coupling arguments (i.e.! = 0). However, these may
be used also in the strong-coupling limit of the pair-
ing process. For example, the linearized version of

23 Electronic Theory for Superconductivity 1441
the gap equation for high-T
c
cuprates in the strong-
coupling limit is given by
Im (k, !)Z(k, !)
=−
1
N
k
∞
−∞
d!
b(§)+f (§ − !)
×
[
P
s
(q, !)−P
c
(q, !)
]
× Im
$
(k
, !
)Z(k
, !
)
(
!Z
)
2
−
k
+
2
&
, (23.50)
where P
s
and P
c
have been defined in (23.23). How-
ever, although lifetime effects of the electrons will
lead to a renormalization of the quasiparticles, the
weak-coupling arguments given above still remain
valid at ! = !
sf
. As in the weak-coupling case, for
decreasing temperature T the eigenvalue (T)in-
creases and passes through unity at T = T
c
.The
derivation of (23.50) is given in Appendix A.
In general, the superconducting order parame-
ter (k, !) does not only yield a gap in the single-
particle density of states, it also sets the scale for the
condensation energy due to the formation of Cooper-
pairs. Therefore, one might expect
T
c
∝
0
,
as in conventional superconductors. This is so in
overdoped cuprates wherethesuperconducting tran-
sition is of mean-field type with a corresponding
coherence length of Cooper-pairs ( ∼ 100Å) and
thus global uniform phase of the Cooper-pairing. In
contrast to this we will see below that in the under-
doped case the number of carriers and density of
Cooper-pairs is small and thus the wave functions
of Cooper-pairs do not overlap significantly. Under
such conditions,also because of the layered structure
of cuprates, it is well known that classical (thermal)
fluctuations of the phases of the Cooper-pairs playan
important role in determining T
c
. Their correspond-
ing energy scale is given by the superfluid density (or
phase stiffness) n
s
[70,78,79]. In such a situation,the
Kosterlitz–Thouless theory or the XY model should
be applicable. Therefore, in the underdoped regime
one already expects from general arguments
T
c
∝ n
s
,
as observedexperimentally by Uemura et al.[14].The
calculation of n
s
, which controls many properties, is
described in the following section.
Tosummarize,wenoteongeneralgroundsthat
for Cooper-pairing via spin fluctuations the under-
lying Fermi surface topology plays an important
role. In particular, for singlet pairing one expects a
d
x
2
−y
2
-wave order parameter if nesting properties are
present.Without nesting one expects no solution for
a repulsive pairing interaction. Furthermore, as we
will show later the nesting properties of the electron-
doped cuprates are weak. Therefore, a competition
between repulsive spin-fluctuation-mediated inter-
action and attractive electron–phonon interaction
may result.A a consequence a transition from d
x
2
−y
2
-
wave order parameter towards anisotropic s-wave
symmetry may occur for T
c
→ 0 and as a function
of doping. In the case of (attractive) triplet pair-
ing no nesting properties are needed and p-wave
symmetry for the superconducting order parameter
would naturally occur if the pairing is dominated
by nearly ferromagnetic spin fluctuations. However,
if strong nesting were present, an order parameter
with f -wave symmetry could win over p-wave sym-
metry. We will see later that the symmetry of the
superconducting order parameter calculated from a
microscopic electronic theory will indeed support
these general arguments.
23.2.6 Superfluid Density n
s
We discuss now the behavior of the superfluid den-
sity n
s
(!, T, x). The frequency ! reflects the dy-
namics of the corresponding quasiparticles and thus
lifetime effects. Note that n
s
controls the doping de-
pendence of the phase coherence, thermodynamic
behavior, the penetration depth, the Nernst effect,
Cooper-pair phase fluctuations, etc.
Obviously, the superfluid density n
s
is a central
property for understanding the superconductivity
and dynamics of the cuprates,in particular of under-
doped cuprates. The superfluid density n
s
(!, T, x)
can be calculated using the current–current correla-
tion function [73] or equivalently from
n
s
m
=
2t
2
(S
N
− S
S
) , (23.51)
