Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

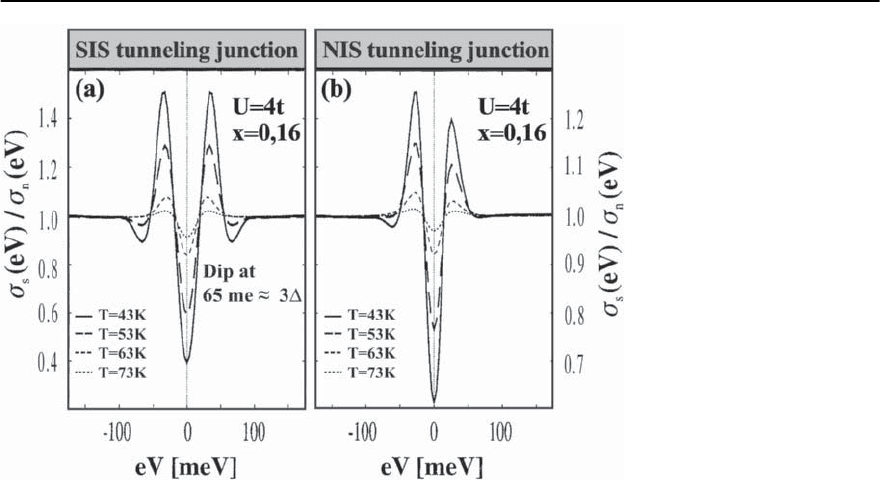
1482 D. Manske,I. Eremin, and K.H.Bennemann

Fig. 23.58. Results for (a)

SIS and (b) NIS tunneling

conductances 

(eV)using

Cooper-pairing theory due

to spin-ﬂuctuation exchange.

Both quantities are normal-

ized by the normal state 

(eV) taken at T = T

.This

is in fair agreement with

experiments [20,99,151]

spin-ﬂuctuation induced Cooper-pairing in high-T

cuprates [99]. It is also interesting to understand why

these dip structures occur at different energies in the

in-plane NIS and SIS measurements. Furthermore,

while the SIS spectrum is symmetric with respect to

the sign of applied voltage the NIS spectra are asym-

metric [151–153].

In Fig. 23.58 we present results [154] for the SIS

and NIS spectra at various temperatures obtained

using the generalized Eliashberg equations.Remark-

ably,bothNIS and SIS tunneling curves show the dip

features at ! = !

res

+

and ! = !

res

+2

,respec-

tively.Thisagrees withexperimentaldata [20,99,151].

In order to better understand the origin of these

peaks let us remember that the experimental tunnel-

ing conductance in NIS is determined by the quasi-

particle density of states as discussed in the section

on theory. As we already know, the density of states

in cuprates is affected by the scattering of the carri-

ers by antiferromagneticspin ﬂuctuations,whichare

peaked in the superconducting state at !

res

.Taking

into account that the whole spectrum will be shifted

by the value of the superconductinggap 

, one con-

cludes that the dip seen in the experiments results

from the peak in the spin excitationsspectra at(, )

shifted by the superconducting gap. Therefore, the

position of the dip in NIS is given by:

NIS–dip: ! ≈ !

res

+ 

In the SIS tunneling both convoluted density ofstates

have to be taken in the superconducting state and

thus the dip in SIS occurs at:

SIS–dip: ! ≈ !

res

+2

This agrees with experiments [99]. Furthermore, in

NIS tunneling the curves are asymmetric due to the

fact that the density of states of the normal state is

asymmetric itself (t



, t



= 0). Thus, the effect will

be visible only for the unoccupied states and also

depends on the shape of the Fermi surface for the

different materials. Therefore, depending on the par-

ticular doping level and material the effect may show

up for the positive biasvoltage or on its negative side.

Our results for SIN and SIS tunneling are similar

to those obtained by the spin–fermion model [156].

Regarding the doping dependence of the “dip” fea-

ture we note that it correlateswith the doping depen-

dence of the“resonance peak”seen in INS. Therefore,

the position of the“dip” feature should have qualita-

tively similar doping dependence as expected from

Fig. 23.46. Finally,we would also like to note that re-

cently it was argued [157] that in many cases the“dip

23 Electronic Theory for Superconductivity 1483

Fig. 23.59. SIStunneling conductance at various

doping levels showing the shift of the dip fea-

ture with T

.Thevoltageaxisisrescaledinunits

of 

/e, taken from [155]. Note that SIS spectra

reveal no pseudogap

feature” seen in bilayer cuprates can be produced by

the effects of bilayer splitting. However, recent stud-

ies of the one-layer Tl-based cuprates [158] confirm

the presence of the“dip”feature indicating its intrin-

sic relation to the ’resonance’ peak. In order to iden-

tify the“dip”position seen in bilayer cuprates and its

relation to the “resonance” peak further studies are

necessary.

In Fig. 23.59 we show the experimental results on

SIS tunneling [155]. One can clearly see that the po-

sition of the dip does not occur exactly at 3

but,

as expected, at 2

+ !

res

.Furthermoreaswasar-

gued in [155] the position of the dip scales simi-

larly to the scaling of the “resonance” peak seen by

INS. Therefore, it appears that the dip structure can

be considered a strong coupling effect analogous to

phonon structures, but the excitations that are re-

sponsible for this feature are the spin ﬂuctuations.

Note that the antiferromagnetic spin ﬂuctuations are

much weaker in the electron-doped cuprates.As a re-

sult the“dip-hump” feature has not been observed in

these compounds so far.

23.4.9 Bilayer Effects

Another interesting effect is the bilayer splitting ob-

served in high-T

cuprates. For a long time it was

believed that the enhancement of T

in two-layer

cuprates resulted from interlayer coupling in the

elementary unit cell. The bilayer splitting was ob-

served only recently by means of ARPES experi-

ments [74,160,161].As expected the bilayer splitting

can be described by the interlayer hopping term

⊥

cos k



cos k

−cosk



where t

⊥

= 70 meV. The matrix element t

⊥

describes

hopping term between the CuO

-planes and k

or  corresponds to the bonding and antibonding

bands, respectively. As a result there are two bands

crossing the Fermi level as shown in Fig. 23.60.

The change in the Fermi surface topology is im-

portant for our theory, since the spin ﬂuctuations

are dependent on the amount of nesting. In the bi-

layered cuprates, due to the introduced hopping be-

tween neighboringCuO

-planes,the topology of the

Fermi surface changes slightly and most importantly

the nesting shifts to the three-dimensional antiferro-

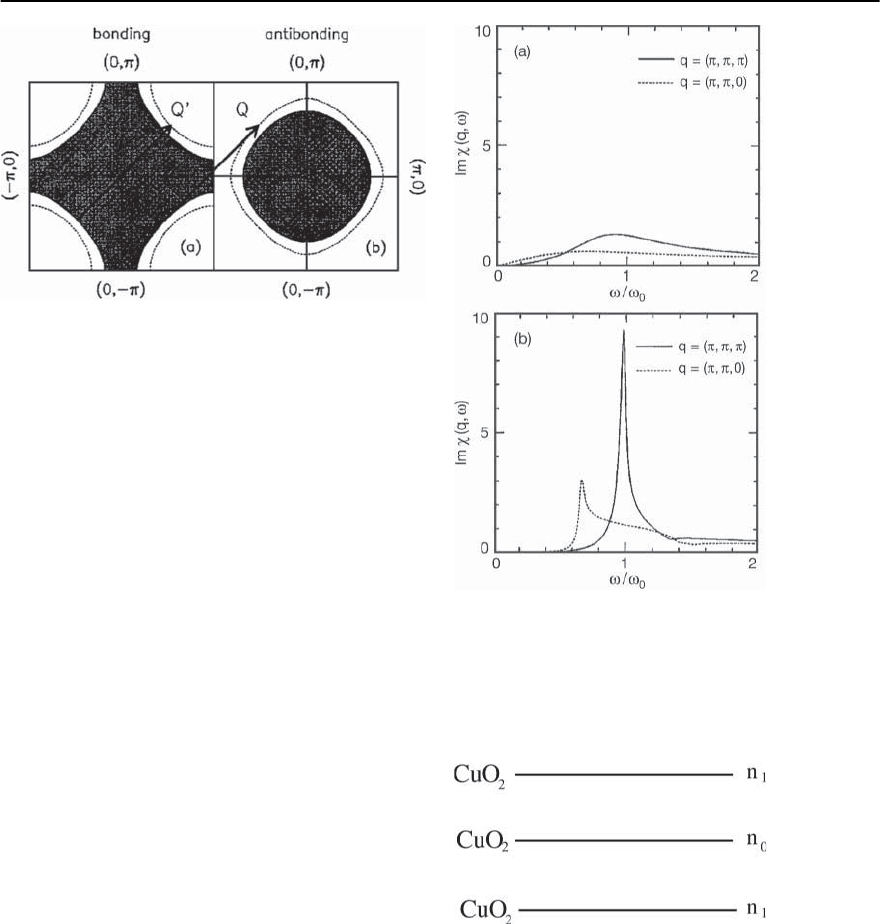
1484 D. Manske,I. Eremin, and K.H.Bennemann

Fig. 23.60. (a) Bonding and (b) antibonding equal energy

contours taken from [159] at optimal doping. The solid

lines bounding the shaded regions are the bonding and an-

tibonding Fermi surfaces, respectively. The arrow labeled

Q corresponds to a (,  , ) momentum transfer, which

dynamically nests the bonding Fermi surface with an ex-

cited antibonding state shown by the dotted curve.Amo-

mentum transfer Q’=( , , 0) nowfails to provide nesting.

This yields a smaller T

for increasing t

⊥

[101]

magnetic wave vector Q



=(, , ). This is shown

in Fig. 23.61.

The change of nesting is also seen in the calcula-

tionof the spin susceptibilityIm(q, !).Thisisillus-

trated in Fig.23.61(a).The peak in Im in the normal

stateismorepronouncedatQ’ rather than for Q,indi-

cating that in the bilayer cuprates the antiferromag-

netic ﬂuctuations are essentially three-dimensional.

Another interesting feature relates to the resonance

peak formation below T

. Similar to the normal state

the “resonance” peak will be more pronounced for

the wave vector Q’ and stronger in its intensity (see

Fig.23.61(b))as compared to the one-layermaterials.

This probably explains why in most cases the reso-

nance peak is visible only in the bilayer cuprates.

What happens with further increase of the num-

ber of CuO

-planes per unit cell? Due to crystallo-

graphic position of the inner CuO

-plane, already

for the three-layer materials its doping concentra-

tion is sufficiently lower than for the two outer ones,

as illustrated in Fig. 23.62. A further increase of the

number of CuO

layers per unitcell does not result in

the enhancement of T

for the same reason. Namely,

the inner planes will be less and less metallic and

already for five-layered compounds the inner CuO

Fig. 23.61. Change of nesting: Results for spin suscepti-

bility Im(Q, !)versus! for Q’=(,  ,  )(solid curve)

and Q=( ,  , 0) (dotted curve)for(a)thenormalstate

at T=T

and (b) the superconducting state at T=T

/2 taken

from [159]. The scales in (a)and(b)arethesameforcom-

parison

Fig. 23.62. Illustration of the change of the doping concen-

tration of CuO

-planes in trilayer cuprates. Due to its crys-

tallographic position the inner CuO

-plane has a smaller

doping than the outer ones. Therefore, the inner CuO

plane will be underdoped. This may effectively reduce the

of the systemifafurtherincreasein the number of layers

takes place. For example, it is known that already in five-

layered cuprate superconductors the inner CuO

-plane is

undoped and remains insulating

23 Electronic Theory for Superconductivity 1485

is non-superconducting. This explains the reduction

of T

with an increasing number of CuO

-planes per

unit cell, n (n > 3).

A final remark we would like to make is on the

value of calculated T

in bilayered cuprates. In the

spin ﬂuctuation scenario and using the FLEX ap-

proximation,T

decreases in the bilayer cuprates due

to a smaller nesting and the corresponding spin ﬂuc-

tuations at Q’. However, this depends on the momen-

tum dependence of the hopping term. Furthermore,

the spin susceptibility 

in the odd channel be-

comes larger than its counterpart in the even channel

(roughly factor5 for realistic parameter values).This

has consequences for the resulting magnitude of the

gap function 

, which also turns out to be larger in

the odd channel. But, all in all, in bilayer cuprates

the essential physics is unchanged. Therefore, the

corresponding “fingerprints” of the spin ﬂuctuation

Cooper-pairing like the “resonance” peak and “dip”

feature seen in INS, and the kink structure in the

elementary excitations seen in ARPES, and SIS/NIS

tunneling spectroscopy should be present. Further

experimental and theoretical studies are expected to

support this.

23.5 Results for Sr

RuO

23.5.1 Electronic Structure

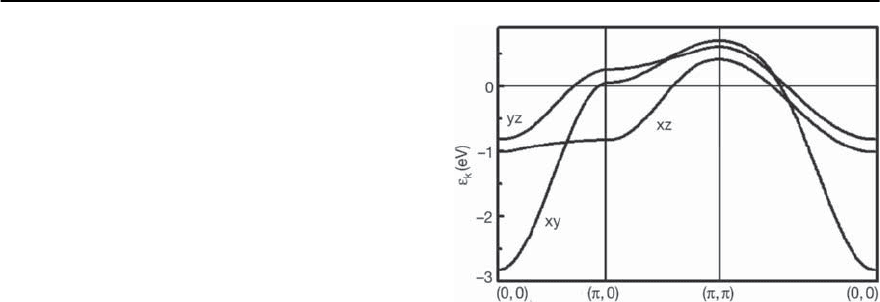
We begin the discussion of our results for Sr

RuO

by analyzing their electronic structure.In contrast to

the cuprates the electronic structure of the ruthen-

ates is more complicated. For example, according

to the LDA calculations there are three bands that

cross the Fermi level [107].Moreover,whileone band

is quasi-two-dimensional (xy), the other two bands

(xz, yz) are quasi-one-dimensional. This is shown in

Fig.23.63 where we present our results for the energy

dispersion of the Sr

RuO

in the RuO

-plane (k

=0)

using the tight-binding parameters and spin–orbit

coupling as described before.

The main effect of the spin–orbit coupling on

the dispersion is the removal of the degeneracy be-

tween xz and yz-bands as present in the LDA cal-

culation. Therefore, one may say that the spin–orbit

coupling acts likea hybridization.On the other hand,

Fig. 23.63. Calculated energy dispersion of the xy , yz,and

xz-bands in Sr

RuO

along the route (0, 0) → (, 0) →

(,  ) → (0, 0) in the first BZ. The tight-binding parame-

ters are used.The spin–orbit coupling is taken into account.

Note that the energy dispersion of the xy( )-band is two-

dimensional, while xz(˛)andyz(ˇ)-bands are sufficiently

one-dimensional as seen from their dispersion

the character of the xz and yz-bands still remains

one-dimensional. This can also be recognized in

Fig. 23.63. For example, one clearly sees that the

xz and yz-bands are weakly momentum dependent

along the (0, 0) → (, 0) and (, 0) → (, )-

directions, respectively. At the same time the xy -

band is two-dimensional. The reason for this is the

strong overlap between the d

Ru orbital with the

and 2p

oxygen orbitals. Since Sr

RuO

shows

a quasi-two-dimensional behavior, it was proposed

originally [54] that only the xy -band plays an impor-

tant role in determining the physical properties of

RuO

in the normal and superconducting states.

Actually, this is further supported by the fact that

the ﬂat region of the xy-band leading to a logarith-

mic singularity in the density of states (the so-called

Van-Hove singularity) lies very close to the Fermi

level.

Yetthequestionabouttheroleofthexz and

yz-bands for determining the physical properties

of Sr

RuO

remains unclear. In Fig. 23.64 we show

the results for the two-dimensional Fermi surface in

ruthenates,which consists of two electron-like Fermi

surfaces of yz nd xy-bands and a hole-like Fermi sur-

face of the xz -band. The filling of each band is ap-

proximately 2/3.The importantfeature that we would

like to stress is a strong nesting of the yz(ˇ)-band

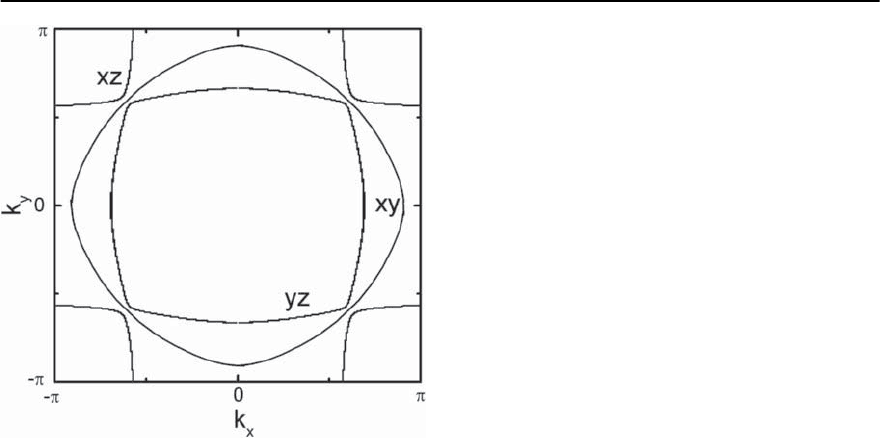
1486 D. Manske,I. Eremin, and K.H.Bennemann

Fig. 23.64. Calculated two-dimensional Fermi surface of

RuO

by taking into account spin–orbit coupling. The

Fermi surface consists of three sheets: two with electron-

like topology and one with hole-like topology. Spin–orbit

coupling acts like a hybridization and removes the degen-

eracy of the ˛(xz)andˇ(yz)-bands

at the incommensurate antiferromagnetic wave vec-

tor Q

=(2/3, 2/3). This is extremely interest-

ing, since it first indicates an importance of the band

structurefordetermining the normal and supercon-

ducting properties of Sr

RuO

andseconditshows

the necessity to include all three bands into the the-

oretical analysis. This is in contrast to the cuprates

where the one-band approximation seems to be in

order mostly.

23.5.2 Elementary Excitations: Effects of Spin

Fluctuations

Unfortunately, the complete analysis of the elemen-

tary excitations including all three bands and spin–

orbit coupling has not been performed so far in

RuO

. However, there have been several attempts

to analyze the behavior of the elementary excitations

in the “most important”  (xy)-band using a pertur-

bation theory up to third order with respect to the

on-site Coulomb interaction U . A three-band Hub-

bard model has been used [162,163].

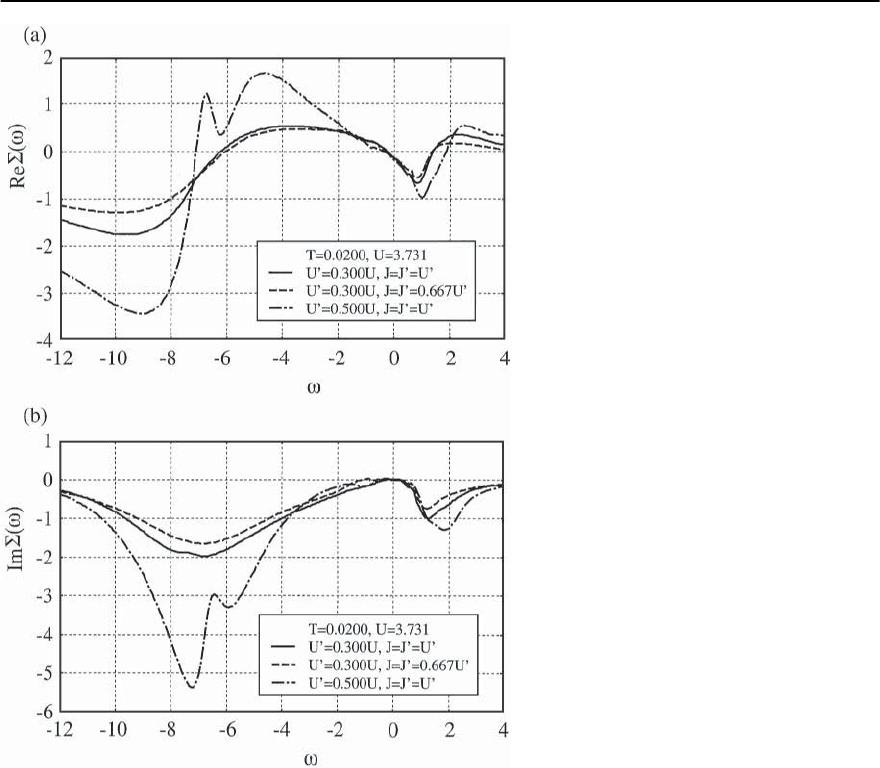
In Fig. 23.65 we show the results for the real and

imaginary parts of the self-energy versus frequency

for different values of Coulomb repulsion (intraband

U and interband U



) and Hund’s coupling (J and



)calculatedatk

for the  -band. As one can see

this band demonstrates the usual Fermi-liquid be-

havior for different values of the inter-orbitcoupling,

Re£(!) ∼ ! and Im£(!) ∼ !

at low energies.

Therefore, it is likely that the nesting in ˛ and ˇ-

bands does not strongly inﬂuencethe low-energy ex-

citations of the  -band that arise due to a presence of

the ferromagnetic-like ﬂuctuations also originating

from the  -band.

On the other hand, at higher energies the self-

energy is sensitive to the inter-orbital interaction,

which can be further observed in the optical con-

ductivity, for example. Another important question

is the behavior of the self-energy in the ˛ and ˇ-

bands. For example, one naively expects that due

to a presence of the strong incommensurate an-

tiferromagnetic ﬂuctuations (IAF) at (2/3, 2/3)

and the quasi-one-dimensional character of these

bandstheir self-energy mayshow a pronouncednon-

Fermi-liquid behavior like in cuprates. Note that

experiments do not show any significant deviation

from the Fermi-liquid behavior. Further studies are

needed.

23.5.3 Dynamical Spin Susceptibility, NMR, and INS

Perhaps one of the most interesting property of the

ruthenates is the dynamical spin susceptibilityin the

normal state. As we discussed in the Introduction,

the understanding of the temperature dependence

of (q, !) is of key significance for determining

the superconducting properties in Sr

RuO

.Letus

study how the two-dimensional three-band Hubbard

Hamiltonian together with the spin–orbit coupling

can explain the existing experimental data.

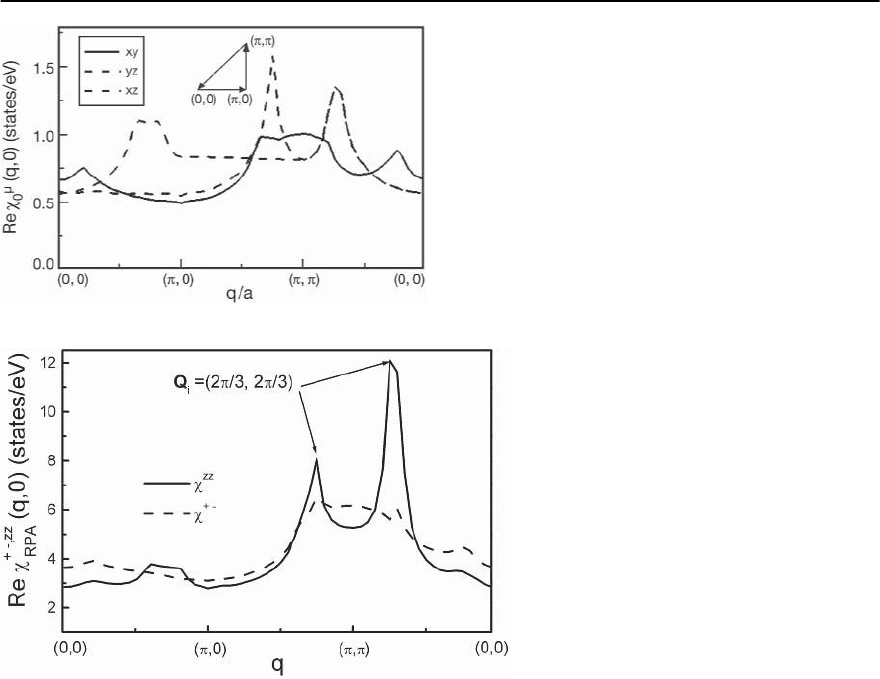
In Fig. 23.66 we show the results for the Lind-

hard response functions calculated for the different

bands using their tight-binding dispersions taken

from LDAcalculations[105].Notethat thespin–orbit

coupling is not taken into account.As expected due to

the pronounced nesting of the xz and yz-bands,their

susceptibilities display peaks at Q

=(2/3, 2/3),

23 Electronic Theory for Superconductivity 1487

Fig. 23.65. The normal state (a)realand(b)

imaginary part of the self-energy for the  -

band taken from [162]. U , U



,andJ, J



refer

to the intraband and interband Coulomb and

Hund’s coupling, respectively. The self-energy

£(!)and! are given in terms of the hopping

integral, t

while the xy-band does not show any significant fea-

ture. The response of the xy -band is enhanced due

to the presence of the van-Hove singularity close to

the Fermi level. It becomes clear that the features

observed by INS relate mainly to the magnetic re-

sponse of the xz and yz-bands. However, the present

results cannot account for the observed magnetic

anisotropy, since both longitudinal and transverse

components of the total spin susceptibility are the

same if the term transferring the anisotropy from the

orbital subspace into the spin subspace is neglected.

In order to do this we include spin–orbit coupling.

Using the random phase approximation (RPA) for

every particular band we calculate the longitudinal

and transverse components of the total susceptibil-

ity in the RuO

-plane using (23.114) and (23.115)

in Sect. 23.3.4. The real part at ! =0isshownin

Fig. 23.67.As a result of the spin–orbit coupling the

magnetic response becomes very anisotropic along

the whole Brillouin zone. Since the spin and or-

bital degrees of freedom are now mixed, the orbital

anisotropy will be reﬂected in the magnetic suscep-

tibility.As one can see in Fig. 23.67 the longitudinal

component has a pronounced peak at Q

,whilethe

1488 D. Manske,I. Eremin, and K.H.Bennemann

Fig. 23.66. Results without spin–orbit coupling: Calculated

real part of the Lindhard spin susceptibility 



( refers to

the band indices) in the normal state of Sr

RuO

along the

route (0, 0) → ( , 0) → (,  ) → (0, 0) in the first BZ

for the three different orbitals (xz,yz,andxy) crossing the

Fermi level.Due to the nesting of the xz and yz-bands their

susceptibilities show an enhancement at the incommensu-

rate antiferromagnetic wave vector Q

=(2 /3, 2/3).The

response of the xy-band is more isotropic, but significantly

larger than in the normal metal due to the vicinity of the

Van-Hove singularity

Fig. 23.67. Calculated real part of the longitu-

dinal and transverse components of the to-

tal RPA spin susceptibility 

+−,zz

RPA







+−,zz

, RPA

( refers to the band indices) in the normal

state of Sr

RuO

along the route (0, 0) →

(, 0) → ( ,  ) → (0, 0) in the first BZ. Due

to spin–orbit interaction the transverse compo-

nent (

+−

) contains not incommensurate anti-

ferromagnetic ﬂuctuations (IAF) from xz and

yz-orbitals, while in the longitudinal compo-

nent (

) they are enhanced

transverse one does not show these features at all

and is almost isotropic (it mostly reproduces the re-

sponse of the xy-band). In order to understand why

thelongitudinal susceptibility mostly shows thenest-

ing features of the xz and yz-bands one has to re-

member that due to spin–orbit coupling the orbital

component of the magnetic susceptibility cannot be

excluded. Therefore, matrix elements such as i|l

|j

and i|l

+(−)

|j have to be taken into account. At the

same time the xz and yz-bands consist of the |2, +1

and |2, −1 orbital states. One can see that while the

longitudinal component gets an extra term due to l

the transverse component does not, since the tran-

sitions between states |2, +1 and |2, −1 are not al-

lowed.Thus,the contributionof the nesting of the xz

and yz orbitals to the longitudinal component of the

susceptibilityis larger than to the transverse one and

incommensurate antiferromagnetic ﬂuctuations are

almost absent.

In order to see this in the inset of Fig. 23.68 we

show the frequency dependence of the longitudinal

and transverse components of Im calculated for the

wave vector Q

=(2/3, 2/3).Despite some struc-

ture seen in the real part of 

+−

RPA

at (2/3, 2/3)

(see Fig.23.67)there areno real incommensuratean-

tiferromagnetic ﬂuctuations (IAF) at this wave vec-

tor. On the other hand, the structure in 

RPA

at the

same wave vector refers to the IAF ﬂuctuations. The

longitudinal component of Im reveals a peak at

approximately !

= 6 meV in quantitative agree-

mentwithINS experimental data [52].The transverse

component is featureless showing the absence of in-

commensurate antiferromagnetic spin ﬂuctuations.

Thus, the ﬂuctuations in the transverse susceptibil-

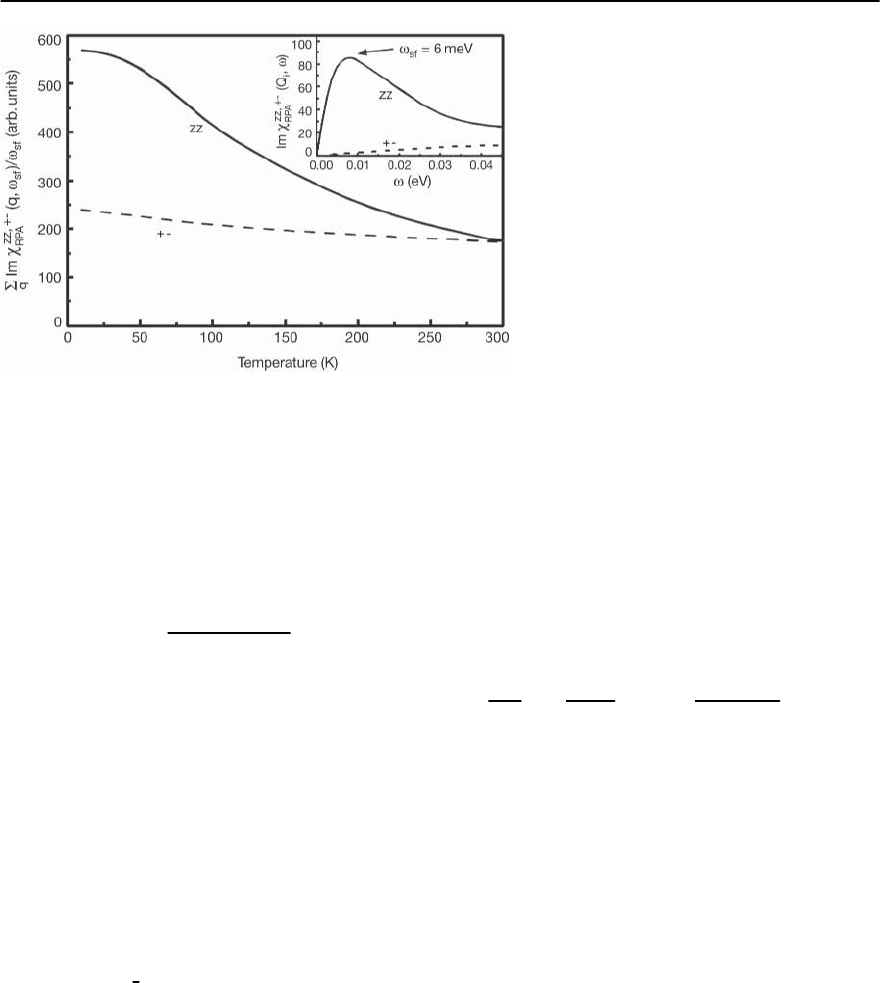
23 Electronic Theory for Superconductivity 1489

Fig. 23.68. Magnetic anisotropy: Temperature

dependence of the imaginary part of the spin

susceptibility divided by !

andsummedover

q. zz and +- refer to the out-of-plane (solid

curve) and in-plane (dashed curve)compo-

nents of the RPA spin susceptibility. In the inset

we show the corresponding frequency depen-

dence of Im

RPA

, !)attheIAFwavevector

=(2 /3, 2 /3) and for !

=6meV

ity are isotropic and ferromagnetic-like. Therefore,

antiferromagnetic ﬂuctuations are present only per-

pendicular to the RuO

-plane.

In order to demonstrate the temperature depen-

dence of the magnetic anisotropy induced by the

spin–orbit coupling in Fig. 23.68 we display the tem-

perature dependence of the quantity



Im

RPA

(q, !

)

for both components.At room temperature bothlon-

gitudinal and transverse susceptibilities are almost

identical, since thermal effects wash out the inﬂu-

ence of the spin–orbit interaction. With decreasing

temperature the magnetic anisotropy increases and

at low temperatures we find the important result that

the out-of-plane component 

is about twice as

large as the in-plane one:



> 

+−

/2 . (23.142)

Ofcourse,thisrelationisonlyvalidclosetothe

wavevector q =

(, ).We also note that our results

are in accordance with earlier estimations made by

Ng and Sigrist [108]. However, there is one impor-

tant difference. In their work it was found that the

IAF are slightly enhanced in the longitudinal com-

ponents of the xz and yz-bands in comparison to the

transverse one. In our case we have found that the

longitudinal component of the magnetic susceptibil-

ity is strongly enhanced due to orbital contributions.

Moreover, by taking into account the correlation ef-

fects within RPA we show that the IAF are even fur-

ther enhanced in the z-direction.

Finally, in order to compare our results with ex-

perimental data we calculate the nuclear spin–lattice

relaxation rate T

−1

for the

OionintheRuO

plane for different external magnetic field orienta-

tion (i = a, b, and c):







(

)







(q, !

)

, (23.143)

whereA

istheq-dependent hyperfine-coupling con-

stant perpendicular to the i-direction.

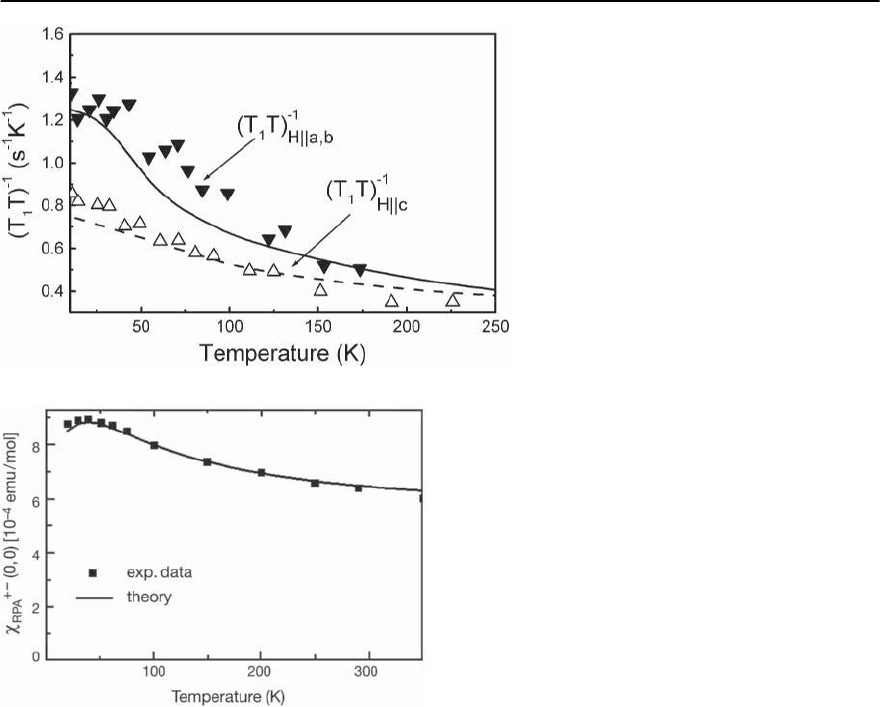
In Fig. 23.69 we show the calculated temperature

dependence of the spin-lattice relaxation for an ex-

ternal magnetic field within and perpendicular to

the RuO

-plane together with experimental data. At

T = 250 K the spin-lattice relaxation rate is almost

isotropic. Due to the anisotropy in the spin suscep-

tibilities arising from spin-orbit coupling the relax-

ationratesbecome increasingly different for decreas-

ing temperature. The largest anisotropy occurs close

to the superconducting transition temperature, in

good agreement with experimental data [110].

It is still important to see whether our theory

yields the weak ferromagnetic ﬂuctuationsobserved

by means of the NMR Knight shift [164]. The latter

1490 D. Manske,I. Eremin, and K.H.Bennemann

Fig. 23.69. Calculated normal state temperature

dependence of the nuclear spin-lattice relax-

ation rate T

−1

OintheRuO

-plane for the

external magnetic field applied along the c-axis

(dashed curve)andalongtheab-plane (solid

curve). Down and up-triangles are experimen-

tal results taken from [110]

Fig. 23.70. The temperature dependence of the uniform

spin susceptibility 

+−

RPA

(0, 0) calculated using our RPA the-

ory in comparison with the

O Knight shift measurements

in the RuO

-plane. The peak is due to thermal activation

involving xy and yz, xz -bands

probes the magnetic ﬂuctuations around q =0.In

Fig. 23.70 we show the results for the temperature

dependence of the uniform susceptibility 

+−

RPA

(0, 0).

One can see that a weak temperature dependence

in fair agreement with experimental data [164] oc-

curs and arises due to ferromagnetic-like ﬂuctua-

tions mainly of the xy-band. Note that very recently

ferromagnetic-like excitations were also observed by

means of INS experiments [165]. This also agrees

with our results.

23.5.4 Superconducting Order P arameter

Triplet superconductivity in Sr

RuO

is of particular

interest. It is important to understand in detail how

the triplet Cooper-pairing is realized in this system

with ferromagnetic and incommensurate antiferro-

magnetic spin ﬂuctuationsat Q

=(2/3, 2/3).We

note that the total spin susceptibility (q, !)con-

trols the symmetry of the superconducting order

parameter. Therefore, the spin–orbit coupling plays

an important role in the superconducting state and

in determining the symmetry of the superconduct-

ing state. First, we present the analysis of the super-

conducting gap without taking the spin–orbit cou-

pling into account. We assume that exchange of spin

ﬂuctuations is responsible for Cooper-pairing. Why

is triplet pairing realized despite the strong IAF at

≈ (2/3, 2/3)?

For the analysis of superconductivity in Sr

RuO

we take into account that experiment observes non-

s-wave symmetry of the order parameter, which

strongly suggests spin-ﬂuctuation-mediated Cooper

pairing. Then assuming spin-ﬂuctuation-induced

pairing it is possible to analyze the symmetry of the

superconducting statefromthe gapequationand our

calculated results for (q, !) with pronounced wave

vectors at Q

and q

. The gap equation is for the band

i given by:

23 Electronic Theory for Superconductivity 1491



=−





eff



(k, k



)]





tanh







(23.144)

where E









is the energy dispersion of

the band i. Note that the pairing potential V

eff



(k, k



)

is different for singlet ( = s)andtriplet( = tr1)

Cooper-pairing. In order to keep the discussion of

the triplet state relatively simple we restrict ourself

to the case of equal spin pairing (i.e. V

eff

tr1

defined

in (23.104)). The eigenvalue analysis of (23.144) will

yield the symmetry with the lowest energy.

For the determination of the pairing potential we

use the calculated FS, the corresponding density of

states, and the spin susceptibility for Sr

RuO

and

also follow the analysis by Anderson and Brinkmann

for

He [114] and by Scalapino forthe cuprates [166].

We compare the results obtained by assuming singlet

or triplet pairing.

For the equal-spin triplet pairing the effective

pairing interaction is given by



eff

tr1

(k, k



)



=−





(k − k



, 0)

1−U

(k − k



, 0)

(23.145)



(k − k



, 0)

1+U

(k − k



, 0)



−2U



(k − k



, 0) ,

where the last term occurs only for ˛ and ˇ-bands.

Note that the first two terms refer to the intraband

spin and charge ﬂuctuations, respectively.

For singlet pairing the effective pairing interac-

tion has the form



eff

(k, k



)





(k − k



, 0)

1−U

(k − k



, 0)

+ (23.146)





(k − k



, 0)



1−U





(k − k



, 0)



− U



(k − k



, 0) .

Again,the first two terms refer to the spin and charge

ﬂuctuations, respectively, and the last term avoids

double counting. Note that the cross-terms includ-

ing 

are small due to the Pauli principle and thus

we neglect them for singlet pairing. Note, the second

term in V

comes from ladder diagrams which due

to the Pauli principle do not contribute to the triplet

pairing.

Using appropriate symmetry representations

[167] we discuss the solutions of (23.144) assuming

p, d,orf -wave symmetry of the order parameter in

the RuO

-plane:



(k)=

ˆz(sin k

a + i sin k

a), (23.147)



(k)=

(cos k

a −cosk

a), (23.148)



−y

(k)=

ˆz(cos k

a −cosk

× (sin k

a + i sin k

a) . (23.149)

Here the ˆz-unit vector refers to the d

component

of the Cooper-pairs as observed in the experiments

[168]. We present the possible explanation for this

later. These symmetries of the superconducting or-

der parameter must be substituted into (23.144).For

simplicity we first consider the solution of (23.144)

in the RuO

-planes and then discuss what is happen-

ing along the c-axis. Note that the largest eigenvalue

of (23.144) will yield the symmetry of the supercon-

ducting order parameter 

in Sr

RuO

Solving (23.144) in the first BZ down to 5 K we

found that p-wave symmetry yields the largest en-

ergy gain for the xy-band, while for the xz and yz-

bands the situation is more complicated.

One can see that the gap equations for the xy and

yz, xz-bands can be separated due to their weak in-

teraction. For the xy -band the p-wave is the most

stable solution, while for the xz and yz-bands f

−y

wave symmetry yields the largest eigenvalue due to

stronger nesting.

Figure 23.71 characterizes the solutions of

(23.144). Note that a good approximation is to lin-

earize (23.144) with respect to 

,i.e.E



→ 



.We

also use tanh(



/2k

T)=1.Thus,themaincontri-

bution to the pairing comes from the Fermi levels.We

present our results for the Fermi surface in the RuO

plane. The wave vectors Q

and q

refer to the peaks

in (q, !). The areas with 

−y

> 0and

−y

< 0

are denoted by (+) and (-), respectively. Notethat the

minus sign in (23.144) is canceled for triplet pairing.

The summation over k



in the first BZ is dominated

by the contributions due to Q

for the ˛ and ˇ-bands

and the one due to q

for the  -band.

As can be seen from Fig. 23.71 in the case of f

−y

wave symmetry for the xy-band the wave vector q

bridges the same number of portions of the FS with