Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.


1452 D. Manske,I. Eremin, and K.H.Bennemann
where a
k,˛
is the Fourier transform of the anni-
hilation operator for the d
˛
orbital electrons (˛ =
xy, yz, zx)andU
˛
is an effective on-site Coulomb
repulsion. The hopping integrals t
k˛
denote the en-
ergy dispersions of the tight-binding bands
k˛
=−
0
−2t
x
cos k
x
−2t
y
cos k
y
+4t
cos k
x
cos k
y
.
(23.88)
In accordance with LDA calculations [105] and ex-
perimental measurements of the Fermi surface and
energy dispersions [106] one chooses for d
xy
, d
zx
,
and d
yz
-orbitals the values for the parameter set
(
0
, t
x
, t
y
, t
) as (0.5,0.42,0.44,0.14),(0.23,0.31,0.045,
0.01), and (0.23, 0.045,0.31, 0.01) eV. This model was
recently applied to Sr
2
RuO
4
[107–109].Its electronic
properties can explain some features of the spin exci-
tation spectruminthe compound Sr
2
RuO
4
.However,
this model neglects spin–orbit coupling and fails to
explain the magnetic anisotropy at low temperatures
observed in NMR experiments [110].
It is known that the spin–orbit coupling plays
an important role in the superconducting state of
Sr
2
RuO
4
.In particular it was shown by Ng and Sigrist
that the spin–orbit coupling lowers the free-energy
and effects superconductivity and the symmetry of
the superconducting order parameter [108].The su-
perconducting state is characterized by the orbital
momentum of the Cooper-pair wave function align-
ing along the z-direction. This so-called chiral state
of the superconducting order parameter is given by
(k)=
0
˜z(sin k
x
± sin k
y
) . (23.89)
Another indication of the importance of the spin–
orbit coupling is the recent observation of the large
spin–orbit coupling in the related insulating com-
pound Ca
2
RuO
4
[111].
Therefore, we extend the theory by adding to the
Hamiltonian givenin (23.87)thespin–orbitcoupling:
H
s−o
=
i
L
i
·
i
. (23.90)
Here, the effective angular momentum L
i
operates
on the three t
2g
-orbitals on the site i and s
i
are the
electron spins. As in an earlier approach [108] we
restrict ourselves to the three orbitals, ignoring e
2g
-
orbitals and choose thecoupling constant such that
the t
2g
-states behave like an l =1angularmomen-
tum representation. Moreover, it is known that the
quasi-two-dimensional xy-band is separated from
the quasi-one-dimensional xz and yz-bands. Then,
one expects that the effect of spin–orbit coupling
is small for the xy-band and can be neglected for
simplicity. Therefore, we consider the effect of the
spin–orbit coupling on xz and yz-bands only. Then,
the kinetic part of the Hamiltonian H
t
+ H
so
can be
diagonalized and the new energy dispersions are
k,yz
=(t
k,yz
+ t
k,xz
+ A
k
)/2 ,
k,xz
=(t
k,yz
+ t
k,xz
− A
k
)/2 , (23.91)
where A
k
=
(t
k,yz
− t
k,xz
)
2
+
2
,and refers to a
pseudo-spin quantum number. The spin–orbit cou-
pling does not break the time-reversal symmetry and
therefore the Kramers degeneracy between the spin
up and down is not removed. The resultant Fermi
surface consists of three sheets as observed in exper-
iment [106]. Most importantly spin–orbit coupling
together with (23.87) leads to a new quasiparticle
which we label by pseudo-spin and pseudo-orbital
indices. The unitary transformation
˜
U
k
connecting
old and new quasiparticle states is defined for each
wave vector and leads to the following relation be-
tween them:
c
+
k,yz+
= u
1k
a
+
k,yz+
− iv
1k
a
+
k,xz+
,
c
+
k,xz+
= u
2k
a
+
k,yz+
− iv
2k
a
+
k,xz+
,
c
+
k,yz−
= u
1k
a
+
k,yz−
+ iv
1k
a
+
k,xz−
,
c
+
k,xz−
= u
2k
a
+
k,yz−
+ iv
2k
a
+
k,xz−
, (23.92)
where
u
mk
=
(t
k,yz
− t
k,xz
∓ A
k
)
2
+
2
, (23.93)
and
v
mk
=
t
k,yz
− t
k,xz
∓ A
k
(t
k,yz
− t
k,xz
∓A
k
)
2
+
2
. (23.94)
The “-” and “+” signs refer to m =1andm =2,
respectively.
Note that despite the spin–orbit coupling causing
the spin and orbit quantum numbers not to be good
ones we can still identify the Cooper-pairing to be

23 Electronic Theory for Superconductivity 1453
triplet or singlet one. This refers then to the pseudo-
spin quantum numbers. At the same time, the mag-
netic behavior of Sr
2
RuO
4
becomes very anisotropic
due to the fact that both one-particle Green’s func-
tions and Lande’s g-factors will be different if the
magnetic field is applied along the c-axisorinthe
ab-RuO
2
-plane. In particular, the anisotropy arises
mainly from the calculations of the Lande’s g-factors
and in particular their orbital parts. The factors
g
z
=
˜
l
z
+2s
z
and g
+
=
˜
l
+
+2s
+
are calculated using
the new quasiparticle states. The latter consist, for
example, of xz and yz-orbitals which in turn are the
combinations of the initial orbital states |2, +1 and
|2, −1 mixed due to the crystal field. Then, the ma-
trix elements |l
+
|(|l
−
|) are zero for the xz-andyz-
orbitals while |l
z
|matrix element is not. Therefore,
the longitudinal components of the spin susceptibil-
ity ofthe xz and yz-band get enhancedin comparison
to the transverse one.An interesting questionthat we
will analyze later is the effect of spin–orbit coupling
on the antiferromagnetic and ferromagnetic fluctu-
ations. This provides insight into a microscopic ex-
planation of the pairing mechanism and allows to
calculate the spatial structure of the superconduct-
ing order parameter.
23.3.2 Eliashberg-Like Theory for the Coupling
of Quasiparticles to Ferromagnetic and
Incommensurate Antiferromagnetic Spin
Fluctuations
For the analysis of the interaction between quasi-
particles and spin fluctuations (ferromagnetic and
incommensurate antiferromagnetic) we proceed as
follows. The form of the electronic theory remains
the same as for the case of cuprates and we extend
the electronic theory towards a three-band theory as
observed in Sr
2
RuO
4
[112,113]. In the normal state
both the self-energy and the thermal Green’s func-
tionsbecome a matrixof 3×3 form,i.e. G
i,j,m
(k, !
n
)
and £
i,j,m
(k, !
n
), where i, j, m refer to the band in-
dexes of the xy, yz, and xz-orbitals.The correspond-
ing Dyson equation is given by
ˆ
G(k, !
n
)
−1
=
ˆ
G
0
(k, !
n
)
−1
−
ˆ
£(k, !
n
) , (23.95)
where
ˆ
G
0
i,j,m
(k, !
n
) is the matrix of the bare Green’s
function determined via the tight-binding energy
dispersions for the xy, yz,andxz-bands. The self-
energy is given by [113]
£
i,j,m
(k, !
n
)=T
q,l
V
1
i,j,m
(q, !
l
) (23.96)
× G
i,j,m
(k − q, !
n
− !
l
) ,
where V
1
i,j,m
(q, !
l
)isaneffectiveinteractionbe-
tween quasiparticles and spin fluctuations.Similarly
as for cuprates it consists of an infinite series of di-
agram including charge and spin fluctuations. How-
ever, some important differences are included in the
random phase approximation.
Most importantly, we consider now the diagrams
shown in Fig. 23.28 with an odd number of bubbles
that contribute to the triplet pairing. This is in con-
trast to singlet pairing in cuprates where an even
number of bubbles occur (see Fig. 23.18). Further-
more, due to the inclusion of the spin–orbit coupling
we expect that the transverse (+-) and the longitudi-
nal (zz) parts of the spin susceptibility are different.
Thus, in the RPA series they have to be summed sep-
arately. Then the effective pairing interaction in the
3×3 form including transverse and longitudinal spin
fluctuations and also charge fluctuations is given by
V
1
i,j,m
(q, !
l
)=
1
2
V
sp,zz
i,j,m
(q, !
l
)+V
+−
i,j,m
(q, !
l
)
−
1
2
V
ch
i,j,m
(q, !
l
) , (23.97)
where
V
sp,zz
= U
2
sp,zz
0
1−U
sp,zz
0
,
V
sp,+−
= U
2
sp,+−
0
1−U
sp,+−
0
(23.98)
describe coupling to spin density fluctuations and
V
ch
= U
2
ch
0
1+U
ch
0
(23.99)
to charge density fluctuations. Here,
ch
0
,
sp,+−
0
are
the irreducible parts of the spin and charge suscep-
tibilities[114].Note that in the Bethe–Salpeter equa-
tion shown diagrammatically in Fig.23.18 for singlet

1454 D. Manske,I. Eremin, and K.H.Bennemann
Fig. 23.28. RPA diagrams for triplet Cooper-pairing with
an odd number of bubbles that refer to longitudinal charge
and spin fluctuations
Cooper-pairing an even number of bubbles and also
ladder diagrams occur. In the case of triplet Cooper-
pairing the contribution of the ladder diagrams is
zero and an odd number bubbles diagrams occur
due to Pauli’s principle shown in Fig. 23.28. Since the
Feynman rules require a (−1) for each loop an extra
minussign entersthegapequationviaV
eff
t
in(23.48).
As described earlier this makes a solution of the gap
equation relatively easy.
The magnetism in the ruthenates resulting from
the quasiparticles in the t
2g
-orbital is itinerant and
thus the magnetic response is created by the same
electrons that also form the Cooper-pairs. Then, for
example, the irreducible part of the charge suscepti-
bility
ch
0
is defined in terms of the electronic Green’s
functions (on a square lattice with size N)
ch
0
(q)=
1
N
k
G(k + q)G(k) , (23.100)
whereG(k) is the one-electron Green’s function (here
weomit thebandindices for simplicity).Thelongitu-
dinal and transverse components of the spin suscep-
tibilitiesare also calculated in terms of the electronic
Green’s functions. In contrast to the cuprates,
sp,zz
0
and
sp,+−
0
in Sr
2
RuO
4
aredifferentduetothemag-
netic anisotropy resulting from spin–orbit coupling.
Todeterminethe superconducting transitiontem-
perature T
c
onemustsolvethefollowingsetoflin-
earized gap equations with eigenvalue
(T), where
refers to the band index ( = ˛, ˇ, ):
,l,m
(k, !
n
)
=−
T
N
k
,!
j
,
V
(2)
,l,m
(k − k
, !
n
− !
j
) G
(k
, !
j
)
× G
(−k
, −!
j
)
,l,m
(k
, !
j
) . (23.101)
Here, the quantum numbers l and m refer to the or-
bital and spin state of a Cooper-pair, respectively.
Note that T
c
is determined from
(T
c
)=1andthe
interband coupling will provide a single T
c
for all
three bands (of course the largest energy gain will be
due to the band having the larger density of states).
In order to simplify the discussion we now focus
mainly onthe -banddueto its largedensity of states.
In the case of singlet pairingone has l =0, 2,...and
m = 0, and for triplet pairing one gets l =1, 3,...
and m = ±1orm = 0. The pairing potential V
(2)
(taken for singlet or triplet pairing) controls which
state gives the lowest energy and determines singlet
or triplet Cooper-pairing.Three possibilities may oc-
cur:
(a) singlet pairing,
(b) triplet pairing with the total spin S
z
=0ofthe
Cooper-pair wave function,
(c) triplet pairing with the total spin S
z
= ±1.
Note that a priori we cannot judge which pairing
state is realized in the ruthenates due to the presence
of both antiferromagneticand ferromagnetic fluctu-
ations. Therefore, one has to solve the gap equations
for all three possibilities.
Thus, for singlet d-wave pairing we would use for
the pairing interaction
V
(2)
s
=
1
2
V
zz
sp
+ V
+−
sp
−
1
2
V
ch
. (23.102)
leading to the linearized gap equation ( = , l =2,
m =0)
=−
T
N
V
(2)
s
GG . (23.103)
Note that due to magnetic anisotropy we separate
the longitudinal and transverse parts of spin fluctu-
ations.
As we will discuss below the magnetic anisotropy
that is due to spin–orbit coupling is in particular very
important for triplet pairing [108].We will see in the
following that it will lift the degeneracy of the three
possible triplet states.In order to demonstratethis we
separate the gap equation into two parts for |m| =1
and m =0.FortripletpairingwithS
z
= ±1wehave
V
(2)
tr1
=−
1
2
V
zz
sp
−
1
2
V
ch
(23.104)
resulting from the set of diagrams with odd num-
ber of bubbles (see Fig. 23.28, all other diagrams are
23 Electronic Theory for Superconductivity 1455
identical to zero) yielding
=−
T
N
V
(2)
tr1
GG . (23.105)
Finally, for triplet pairing with S
z
=0weget
V
(2)
tr0
=
1
2
V
zz
sp
− V
+−
sp
− V
ch
, (23.106)
and the gap equation
=−
T
N
V
(2)
tr0
GG . (23.107)
This clearly demonstrates the importance of spin–
orbit coupling for the magnetic anisotropy and thus
for the pairing interaction. Obviously, if no mag-
netic anisotropy would be present, i.e.
+−
=2
zz
,
one obtains the same gap equation for |m| =1and
m = 0. Therefore, we safely conclude that the impor-
tant magnetic anisotropy selects one of the triplet
state (
zz
>
+−
) lifting the degeneracy. As we will
discuss in Sect. 23.5.4,ferromagnetic fluctuations fa-
voring triplet pairing are mainly present in
+−
and
thus in V
+−
sp
. This will lower the energy for the m =0
triplet state.
Obviously, the magnetic anisotropy described
above that enters the Eliashberg-like theory will lead
to interesting effects if an external magnetic field
h
ext
is applied. For example, the anisotropy of the
ratio h
⊥
c2
/h
||
c2
and its connection to the internal struc-
ture of the superconducting order parameter will be
discussed in Sects. 23.3.4 and 23.5.4.
23.3.3 Elementary Excitations in Sr
2
RuO
4
The behavior of the elementary excitations in
ruthenates is controlled by the spin fluctuations:
!
k
=
k
+ £(k, ! = !
k
) . (23.108)
Here, the self-energy £(k, !) results mainly from
the coupling to spin fluctuations. Clearly, since the
anisotropic spin susceptibility (k, !) is the impor-
tant input for £, the self-energy and thus the el-
ementary excitations are affected by the magnetic
anisotropy.Note that the spin fluctuations in ruthen-
ates are highly anisotropic. Strong incommensurate
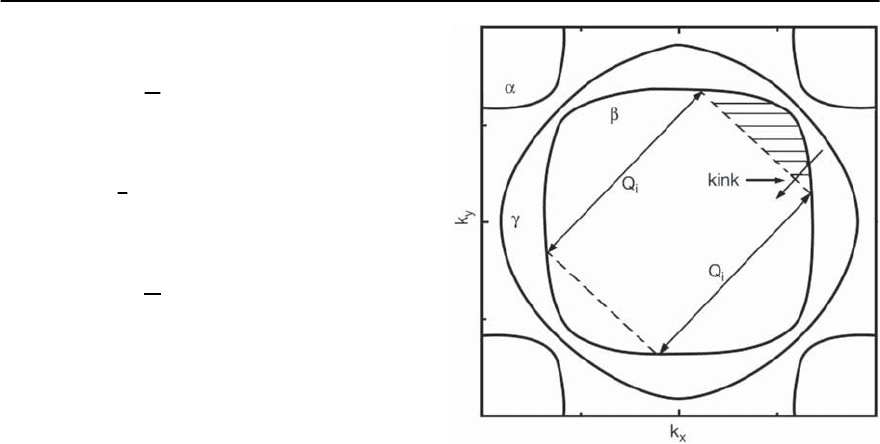
Fig. 23.29. Expected“kink”structure in Sr
2
RuO
4
.TheFermi
surface in Sr
2
RuO
4
consists of three bands. The nest-
ing properties of the yz(ˇ)-band reveal the formation
of two-dimensional incommensurate spin fluctuations at
Q
i
=(2 /3, 2 /3) and !
sf
≈ 6 meV. The quasiparticles
at the ˇ-band reveal a strong renormalization due to scat-
tering by spin fluctuations. Thus, a corresponding “kink”
formation foroccupied statesbelow E
F
(shaded area)along
certain direction in the first BZ as indicated by the arrow
may occur
antiferromagnetic fluctuations at the wave vector
Q
i
=(2/3, 2/3) and !
sf
= 6meV are present
in Sr
2
RuO
4
only in the quasi-one-dimensional xz(˛)
and yz(ˇ)-bands. Similar to the cuprates, we ex-
pect also the formation of the “kink” feature due to
spin fluctuations as shown in Fig. 23.29. On general
grounds a“kink” structure occurs in the energy dis-
persion of the ˇ-band belowE
F
forthe quasiparticles
that are connected by the corresponding wave vector
Q
i
and !
sf
. Note that according to the relation
!
kink
= !
sf
+
yz
k+Q
i
(23.109)
the “kink” energy will be smaller than in cuprates
duetoalowervalueof!
sf
in the ruthenates.
So far, a “kink” has only been observed in the -
band [115].This is interesting because the quasipar-
ticles in the xy( )-band do not experience the scat-
tering by antiferromagneticspin fluctuationsand in-

1456 D. Manske,I. Eremin, and K.H.Bennemann
teract mainly with weak ferromagnetic fluctuations.
Thus, one expects mainly a Fermi-liquid-type of be-
havior forthe quasiparticlesin the xy-band.Further-
more,due to a smallvalueof thesuperconducting gap
(
0
!
sf
) there will be no noticeable feedback of
superconductivity on the “kink” feature.
23.3.4 Dynamical Spin Susceptibilit y: Magnetic
Anisotropy
Let us analyze the dynamical spin susceptibility in
Sr
2
RuO
4
. Due to the mixing of the spin and or-
bital degrees of freedom, the magnetic susceptibil-
ity also involves the orbital magnetism which is very
anisotropic.
For the calculation of the transverse,
+−
l
,and lon-
gitudinal,
zz
l
, components of the spin susceptibility
of each band l we use the diagrammatic representa-
tion shown in Fig. 23.30. Note that the Kramers de-
generacy is not removed by the spin–orbit coupling,
since the latter does not remove the time-reversal
symmetry and G
l
k+
= G
l
kz
.Thus,the anisotropy arises
mainly from the calculations of the Lande’s g-factors
and in particular their orbital parts. The factors
g
z
=
˜
l
z
+2s
z
and g
+
=
˜
l
+
+2s
+
are calculated us-
ing the new quasiparticle states. The latter consist,
for example, of xz and yz-orbitals, which in turn are
the combinations of the initial orbital states |2, +1
and |2, −1 mixed due to the crystal field. Then, the
matrix elements |l
+
|(|l
−
|) are zero for the xz and
yz-orbitals while |l
z
| matrix element is not. There-
fore,the longitudinal components of the spin suscep-
tibility of the xz and yz-band are enhanced in com-
parison to the transverse one.We obtain,for example,
for the |xz-states for the transverse susceptibility
+−
0,xz
(q, !)=−
4
N
k
(u
2k
u
2k+q
− v
2k
v
2k+q
)
2
×
f (
+
kxz
)−f (
−
k+qxz
)
+
kxz
−
−
k+qxz
+ ! + iO
+
, (23.110)
and for the longitudinal susceptibility
zz
0,xz
(q, !)=
↑
xz
(q, !)+
↓
xz
(q, !)
=−
2
N
k
u
2k
u
2k+q
+ v
2k
v
2k+q
+
√
2(u
2k
v
2k+q
+ v
2k
u
2k+q
)
2
×
f (
+
kxz
)−f (
+
k+qxz
)
+
kxz
−
+
k+qxz
+ ! + iO
+
. (23.111)
Here, f (x) is again the Fermi function and u
2
k
and v
2
k
are the corresponding coherence factors defined in
(23.93)–(23.94).
For all other orbitals the calculations are simi-
lar and straightforward. Note that the magnetic re-
sponse of the xy-band remainsmainly isotropic.This
is due to the absence of the nesting features in the xy-
band.
Then, one gets within RPA the following expres-
sions for the transverse susceptibility (
˜
l =−l):
+−
RPA,l
(q, !)=
+−
0,l
(q, !)
1−U
+−
0,l
(q, !)
, (23.112)
and for the longitudinal susceptibility
zz
RPA,l
(q, !)=
zz
0,l
(q, !)
1−U
zz
0,l
(q, !)
, (23.113)
where
zz
0,l
=
++
0,l
+
−−
0,l
.
Fig. 23.30. Diagrammatic representation of (a) the longitudinal and (b) the transverse magnetic susceptibility. The full
lines represent the electron Green’s function with pseudo-spin and pseudo-orbital
˜
l quantum numbers. The Lande’s
g-factors are denoted by g
+
=
˜
l
+
+2s
+
(g
−
=
˜
l
−
+2s
−
)andg
z
=
˜
l
z
+2s
z
23 Electronic Theory for Superconductivity 1457
These susceptibilitiesare used in the correspond-
ing pairing interaction fortriplet pairing.In order to
compare our results with NMR and INS experiments
we take
zz
tot
=
l
zz
RPA,l
(23.114)
and
+−
tot
=
l
+−
RPA,l
. (23.115)
23.3.5 Gap Equation: Triplet Pairing and Symmetry
of the SuperconductingOrder Parameter
The interesting question in the ruthenates is how
can triplet Cooper-pairing with the possible pair
states
±
| ↑↑, m
z
=+1
| ↓↓, m
z
=−1
and
0
1
√
2
(
|↑↓+|↓↑
)
, m
z
= 0 (23.116)
occur in the presence of strong incommensu-
rate antiferromagnetic spin fluctuations at Q
i
=
(2/3, 2/3) originating from the xz and yz-bands
and weaker ferromagnetic fluctuations arising from
the xy -band. For the interplay of the antiferromag-
netic and ferromagnetic-like spin excitations the
magnetic anisotropy,
zz
(Q
i
) >
±
(Q
i
), is very sig-
nificant. This anisotropy will also lift the degener-
acy of the three possible triplet states and favor for
the Cooper-pairs the state
0
∼
1
√
2
(
|↑↓+|↓↑
)
.
Note that the magnetic anisotropy is caused by spin–
orbit coupling. The above three triplet Cooper-pair
states with magnetic quantum numbers m
z
= ±1, 0
result from the transverse and longitudinal spin ex-
citations. Therefore, the important normal-state re-
sult
zz
(Q
i
) >
+−
(Q
i
) already suggests lifting of the
triplet states degeneracy and the realization of the
m
z
=0state
1
√
2
(
|↑↓+|↓↑
)
.
In the case of a dominating -band, with a large
density of states, it follows almost directly from the
Fermi surface topology illustrated in Fig. 23.31 that
triplet Cooper-pairing mediated by ferromagnetic
excitations occurs.
Of course, the gap equation determines the occur-
rence of the triplet state with m
z
= 0. Note that the
order parameter for triplet Cooper-pairing can be
writtenintheform
k
=
d
(k)(
i
2
)
=
−d
x
+ id
y
d
z
d
z
d
x
+ id
y
. (23.117)
Again as in the cuprates all chosen symmetries must
be irreducible representations of the D
4h
crystallo-
graphic point group symmetry, since the crystal field
potentialisverystronginruthenatesaswellasin
cuprates. The full set of them was found by Sigrist
and Rice [116]. Experimentally it is confirmed that
in Sr
2
RuO
4
(close to T
c
)onlythed
z
= ˆz component
of the superconducting order parameter is present
while the d
x
= ˆx and d
y
= ˆy component is strongly
suppressed [53].
Fig. 23.31. Calculated Fermi surface (FS) topology for
Sr
2
RuO
4
and symmetry analysis of the superconducting
order parameter in the first Brillouin zone. The real part
of a p-wave order parameter has the node along k
x
=0. +(-)
and the dashed lines refer to the signs of the momentum
dependent order parameter of . ˛, ˇ,and denote the
FS of the corresponding (hybridized) bands. The Cooper-
pairing wave vectors Q
i
and q
i
refer to maxima in the spin
susceptibility and provide the main contribution to the
pairing instability
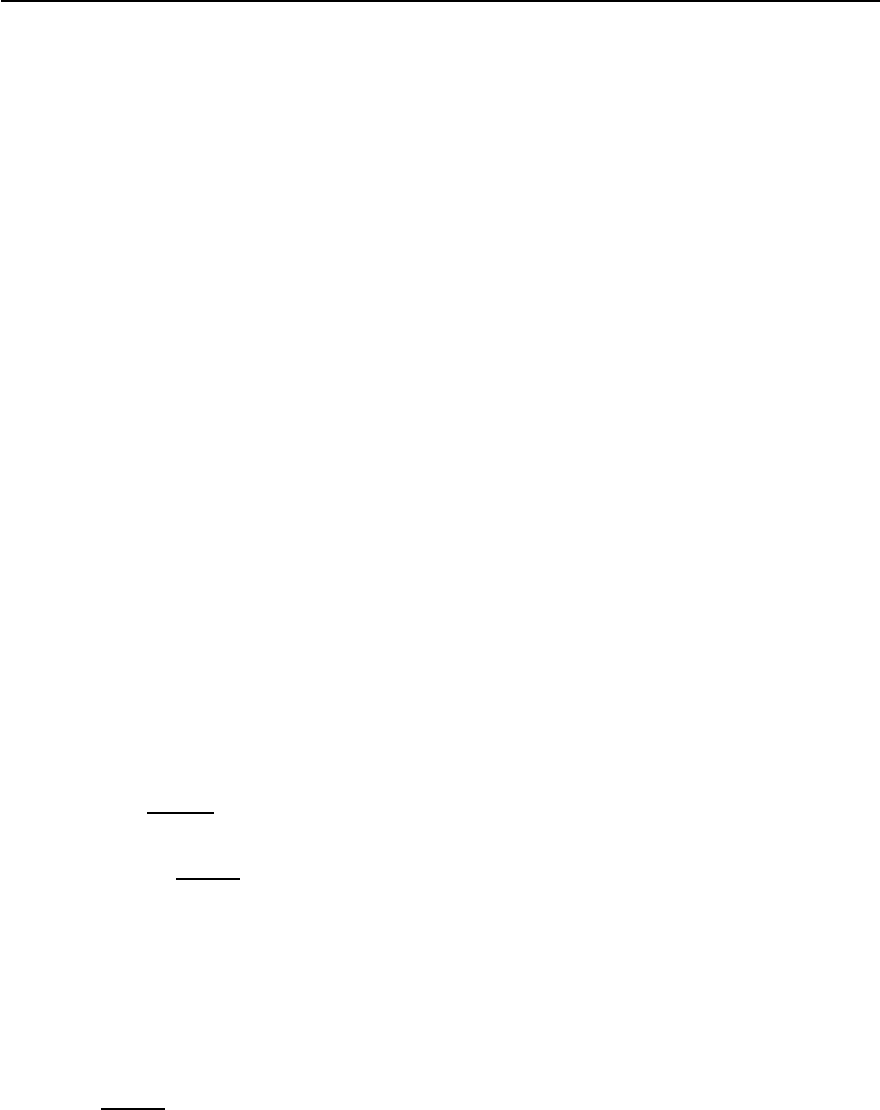
1458 D. Manske,I. Eremin, and K.H.Bennemann
For a discussion of the symmetry of the order pa-
rameter it is instructiveto consider the Fermi surface
topology and the structure of (q). Thus, in order to
investigate triplet pairing in Sr
2
RuO
4
in more de-
tail, in Fig. 23.31 we show its corresponding Fermi
surface topology obtained from the three-band Hub-
bard Hamiltonian discussed earlier in this chapter.
However, for simplicity we discuss here only the -
band, which has a high density of states. The effects
due to the other bands (˛ and ˇ) will be analyzed in
detail later. For the moment and for simplicity let us
discuss only the -band in order to study the differ-
ences between Sr
2
RuO
4
and cuprates.
Sr
2
RuO
4
shows a two-dimensional electronic
structure, which indicates that the Cooper-pairing
mainly occurs in the RuO
2
-plane. Thus, we discuss
first the superconductivity in the RuO
2
-plane and
then analyze what happens along the c-direction.
A closer inspection of (23.49) shows that |
p
|
2
has
no nodes. However, Re
p
(also Im
p
) indeed has
a nodal line also displayed in Fig. 23.31. This has
important consequences if strong nesting is present.
Then, f -wave symmetry of the superconducting or-
der parameter wins over p-symmetry. This can be
seen as follows (for simplicity we restrict the discus-
sion to the case of equal spin pairing, i.e. m
z
= ±1):
The summation over k
in the first BZ is dominated
by the contributions due to Q
pair
and the one due
to a smaller wave vector q
pair
(see (q, !)). Thus,
we obtain approximately for the -band contribu-
tion (angular quantum number l = f or p)
l
(k) ≈
i
V
eff
tr1
(Q
i
)
2
k+Q
i
l
(k + Q
i
)
+
i
V
eff
tr1
(q
i
)
2
k+q
i
l
(k + q
i
) , (23.118)
where the sum is over all contributionsdueto Q
i
and
q
pair
. The wave vectors Q
pair
bridgeportionsof the FS
where Re
p
has the opposite sign. Since the smaller
wave vector q
pair
bridges areas on the Fermi surface
with same sign. Contributions with opposite signs
occur and thus
i
V
eff
tr1
(q
i
)
2
k+q
i
l
(k + q
i
) ≈ 0 . (23.119)
Hence,we find a gap equation where
l
is expected to
changeitssign for an attractive interaction and dom-
inating Q
i
transitions. However, this is not possible!
In other words, if the corresponding pairing interac-
tion involves strong nesting similar to cuprates,i.e.a
peak of
RPA
at q ≈ Q
pair
, Cooper-pairing and a p-
symmetry solution of (23.49) would not be possible
due to V
eff
t
< 0. Nesting properties would suppress
the p-wave and favor the f -wave, and then one would
get (for f -symmetry)
f
(k)=
0
ˆz(cos k
x
−cosk
y
)(sin k
x
+ i sin k
y
) .
(23.120)
Like the d
x
2
−y
2
-wave order parameter in cuprates the
f -wave symmetry order parameter has also nodes
along the diagonals. Note that ˜z indicates that only
the d
z
component of the superconducting order pa-
rameter is present.
However, note that for weaker nesting and for
ferromagnetic spin fluctuations one expects that p-
wave symmetry wins over f -wave symmetry triplet
Cooper-pairing. Obviously,the magnetic anisotropy
observed in Sr
2
RuO
4
is important for this.
Theoddparityofthesuperconductingorderpa-
rameter and strong reduction of T
c
by non-magnetic
impurities suggests that electron–phonon interac-
tion does not cause superconductivity in Sr
2
RuO
4
.
Note that the recently observed negative isotope ef-
fect (˛ =−0.15) indicates the complicated depen-
dence of the isotope mass from interaction parame-
ters [117].
One expects on general grounds that the singlet
Cooper-pairing will not be realized in the ruthen-
ates. The simple reason behind this is that the an-
tiferromagnetic fluctuations favoring singlet pair-
ing with d
x
2
−y
2
-wave symmetry of the superconduct-
ing order parameter originate from the quasi-one-
dimensional xz and yz-bands. However, the xy-band
with only weak ferromagnetic fluctuations has a
much larger density of states at the Fermi level. This
indicates its large contribution to superconductiv-
ity. Therefore, the xy-band will not be unstable with
respect to the singlet Cooper-pairing. This is illus-
trated in Fig.23.31.Notethat ford
x
2
−y
2
-wave symme-
try we get a change of sign of the order parameter
upon crossing the diagonals of the BZ. For the sin-
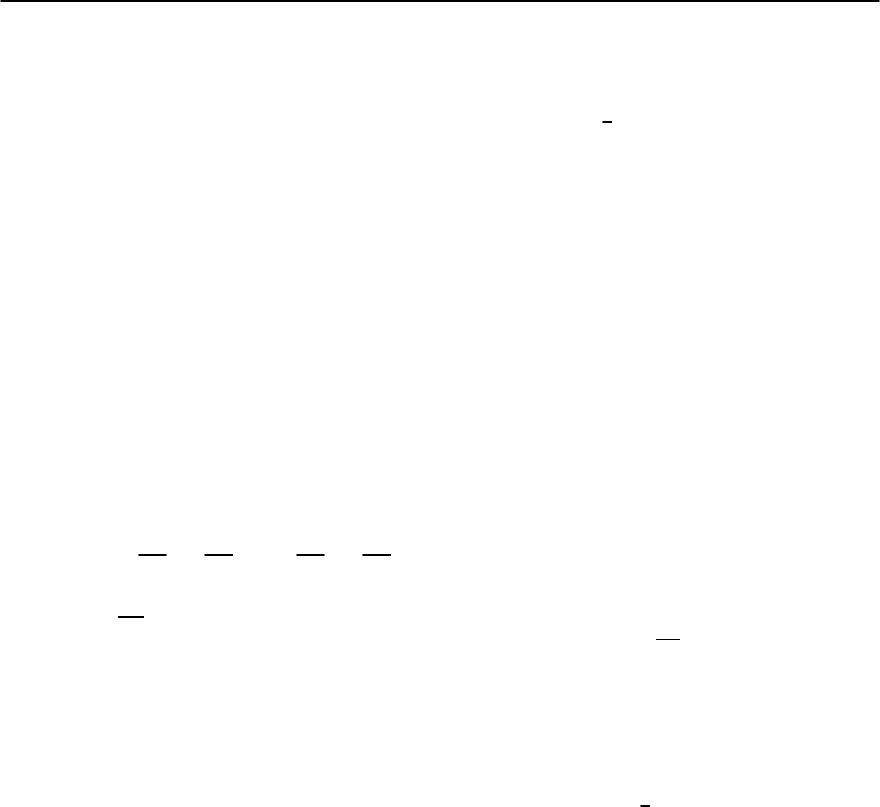
23 Electronic Theory for Superconductivity 1459
glet Cooper-pairing the wave vectors around Q
i
con-
necting areas (+) and (-) contribute constructively
to the pairing. Contributions due to q
i
and the back-
ground connecting areas with the same sign subtract
from the pairing (see Fig. 23.31 with nodes at the
diagonals). Therefore, we get that the four contribu-
tions due to q
i
in the xy-banddonotallowtohave
d
x
2
−y
2
-wave symmetry in the xy-band. Despite the
pair-building contribution due to Q
i
one gets that
theeigenvalueofthed
x
2
−y
2
-wave symmetry in the
xy-band is smaller than for the f
x
2
−y
2
-wave symme-
try.This isduetothelargecontributionfromQ
i
to the
cross-terms for the triplet pairing, which are absent
for the singlet pairing. For d
xy
-symmetry where the
nodes are along (,0) and (0,)directionsweargue
similarly. Thus, we may exclude this symmetry.
What is the situation with the RuO
2
-planes? First,
due to a weak dispersion the electronic bands along
c-direction one may expect a weak dispersion of the
superconducting p-wave gap:
k
=
0
˜z
sin
k
x
a
2
cos
k
y
a
2
+ i sin
k
y
a
2
cos
k
x
a
2
× cos
k
z
c
2
. (23.121)
Note that due to the cosine function the supercon-
ducting gap will have a node for the k
z
= /c.On
the other hand, the formation of the node in the su-
perconducting order parameter usually reflects the
underlying structure of the pairing potential.In our
case this results from the spin susceptibility, which
becomes anisotropic due to spin-orbit coupling. In
particular, the antiferromagnetic spin fluctuations
are polarized along the c-direction,while ferromag-
netic fluctuations are mainly present in the RuO
2
-
plane. Then, the polarized antiferromagnetic spin
fluctuations could be one of the reasons for the node
formation away from the RuO
2
-plane in Sr
2
RuO
4
.
This we will discuss later.
What happens if an external magnetic field is ap-
plied?As in superfluid
3
He there exists an interesting
effect concerning the possible change of the orienta-
tion of the unit vector d
z
= ˆz of the superconducting
order parameter.In general, the spin susceptibility is
a tensor in spin space with principal axes along the
preferred directions. Therefore the magnetic energy
density
f
h
=−
1
2
h
h
(23.122)
depends on the orientation of the susceptibility ten-
sor and hence on the order parameter itself. As we
have discussed in the Introduction the spin suscep-
tibility of Sr
2
RuO
4
in the superconducting state be-
haves differently fordifferent orientationof the mag-
netic field. For example for h ⊥ d (i.e an external
magnetic field is applied along the a or b-direction)
the susceptibility is unchanged with respect to its
normal state value
N
[118]. On the contrary, when
h||d the susceptibility becomes gapped, the temper-
ature dependence of which is described by the so-
called Yoshida function [118]. Therefore, the spin
susceptibility in Sr
2
RuO
4
depends strongly on the
relative orientation of d and h. In its general form
the susceptibility tensor reads
=
0
N
{ı
−
ˆ
d
ˆ
d
[
1−Y
0
(T)
]
}, (23.123)
where Y
0
(T)=−
∞
−∞
dE
k
df
k
dE
k
is the Yoshida function.
One finds that for the magnetic field applied along
the c-direction, the susceptibility and consequently
the magnetic energy gets a contributionwhich tends
to orient d perpendicular to the magnetic field
f
h
=
1
2
(d · h)
2
, (23.124)
where =
0
N
(1 − Y
0
(T)). This means that for a
relatively large magnetic field applied along the c-
direction the significant d
x
and d
y
components in the
superconducting order parameter in Sr
2
RuO
4
can be
induced. This possibility is already known from su-
perfluid
3
He. Of course, as in
3
He, this effect is rela-
tively small but observable. This is a subject of fur-
ther experimental studies.
In the following we present results for impor-
tant properties of the superconducting state.First we
discuss superconductivity of cuprates, then that of
ruthenates.
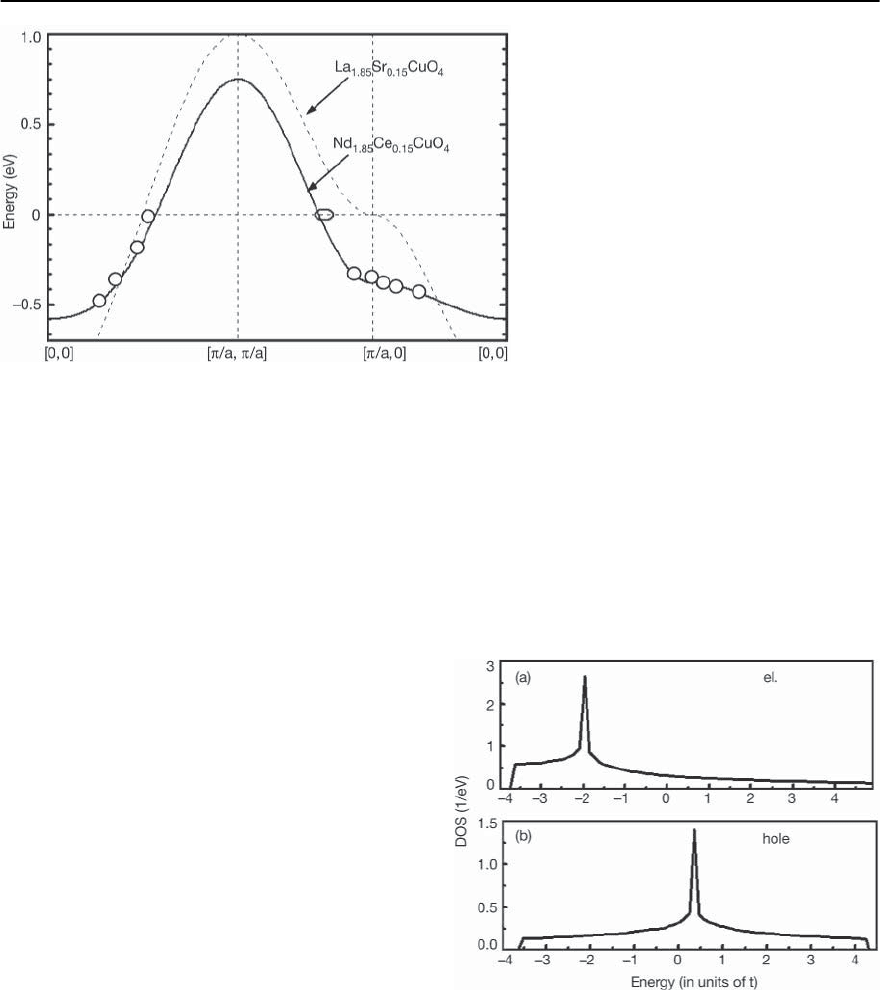
1460 D. Manske,I. Eremin, and K.H.Bennemann
Fig. 23.32. Calculated energy dispersion for the
hole-doped and electron-doped cuprates at
optimal doping concentration. We use t =
250 meV and t
= 0 for the hole-doped cuprates
(dashed curve)andt = 128 meV and t
=−0.3
for the electron-doped cuprates (solid curve).
The experimental data (open symbols)taken
from [104].The position of the flat bands in the
electron-doped cuprates is 300 meV below E
F
.
On the other hand, in most of the hole-doped
cuprates the van-Hove singularity lies close to
the Fermi level
23.4 Results for H ole-Doped and
Electron-Doped Cuprates
We present results for key properties of cuprate
superconductivity using as a model the Hubbard
Hamiltonian and Eliashberg-like theory and assum-
ing Cooper-pairing due to spin fluctuations. Impor-
tant input for the calculations is the electronic band
structure. A comparison of the calculations with ex-
periments should further justify the validity of our
theory. We find d
x
2
−y
2
-wave superconductivity for
both hole-doped and electron-doped cuprates. The
elementary excitations and the doping dependent
phase diagram are central results.
23.4.1 Bare Electronic Structure
In Fig. 23.32 we present results for the energy disper-
sion along the route (0, 0) → (, 0) → () →
(0, 0) of the first Brillouin zone for hole-doped
and electron-doped cuprates at optimal doping. As
a typical example we refer to La
2−x
Sr
x
CuO
4
and
Nd
2−x
Ce
x
CuO
4
. It is known that the position of the
flat bands with respect to the Fermi level is described
by the ratio of t
/t. Using the fact that in hole-doped
cuprates the flat bands lie close to the Fermi en-
ergy while in the electron-doped ones they lie much
lower,this ratio is expected to be small in hole-doped
cuprates, while in electron-doped cuprates we ap-
proximate t
/t =−0.3 in order to describe the exper-
imental results.
The corresponding densities of states are shown in
Fig.23.33.The flat bands reflecting the so-called van-
Hove singularity are a common feature of cuprates
having a two-dimensional square lattice. Note again
that the bands are at different energies in hole-doped
and electron-doped cuprates. Due to the fact that in
hole-doped cuprates the van-Hove singularity lies
near the Fermi energy, these are closer to an an-
tiferromagnetic instability than the electron-doped
ones. Therefore, antiferromagnetic spin fluctuations
Fig. 23.33. Results for the density of states in (a)electron-
doped and (b) hole-doped cuprates using the energy dis-
persion shown in Fig. 23.32. The so-called van-Hove singu-
larity that originates from the flat part of the conduction
bands in hole-doped cuprates lies much closer to the Fermi
energy (
F
= 0) than in electron-doped cuprates
23 Electronic Theory for Superconductivity 1461
in the hole-doped cuprates are expected to be much
stronger due to the nesting. As a consequence more
phase space is available for Cooper-pairing.
Note that this does not contradict the experimen-
tal data, which indicate a large doping range of anti-
ferromagnetism in electron-doped cuprates. As has
beenshown earlier [63,119]thesmalldopingrangeof
antiferromagnetism in hole-doped cuprates is due to
spin frustration that arises from holes at the oxygen
sites. In contrast in the electron-doped cuprates only
a dilution of the Cu-spins takes place and thus as a
consequence antiferromagnetism occurs over larger
doping range.
Theinput (material-dependent)parameters of the
theory will play an important role in our calculations
and will explain the observed asymmetry between
electron-doped and hole-doped cuprates. Moreover,
since thetopology of theFermi surface andthe corre-
sponding position of the flat bands change with dop-
ing, we also expect the characteristic changes in the
behavior of hole-doped and electron-doped cuprates
with doping.
We would like also to note that many of the hole-
doped cupratescontaintwo CuO
2
-planesperunitcell
and that this requires the inclusion of bilayer effects
into ourtheory.Wewill study thislater,butwould like
to stress that the main features that will be obtained
within a one-band calculation will already describe
the main experimental facts of the cuprates.
23.4.2 Elementary Excitations
Let us first discuss the elementary excitations. The
results for the spectral density due to the scatter-
ing of the carriers by antiferromagnetic spin fluctu-
ations are expected to exhibit fundamental behavior.
As we have shown the dispersion of the carriers will
be modified by the self-energy, £, arising from the
coupling of the quasiparticles to antiferromagnetic
spin fluctuations:
!
k
=
k
+Re£(k , ! = !
k
) .
Note that the renormalization of
k
by £(k, ! = !
k
)
will be characteristically anisotropic.
1. Nodal Direction
We start the discussion analyzing thespectral density
of hole-doped superconductors in the normal state.
The spectral density reveals the elementary excita-
tions and in particular the renormalized energy dis-
persion. First, we present our results for the spectral
density along the nodal (0, 0) → (, )-directionin
the first BZ.
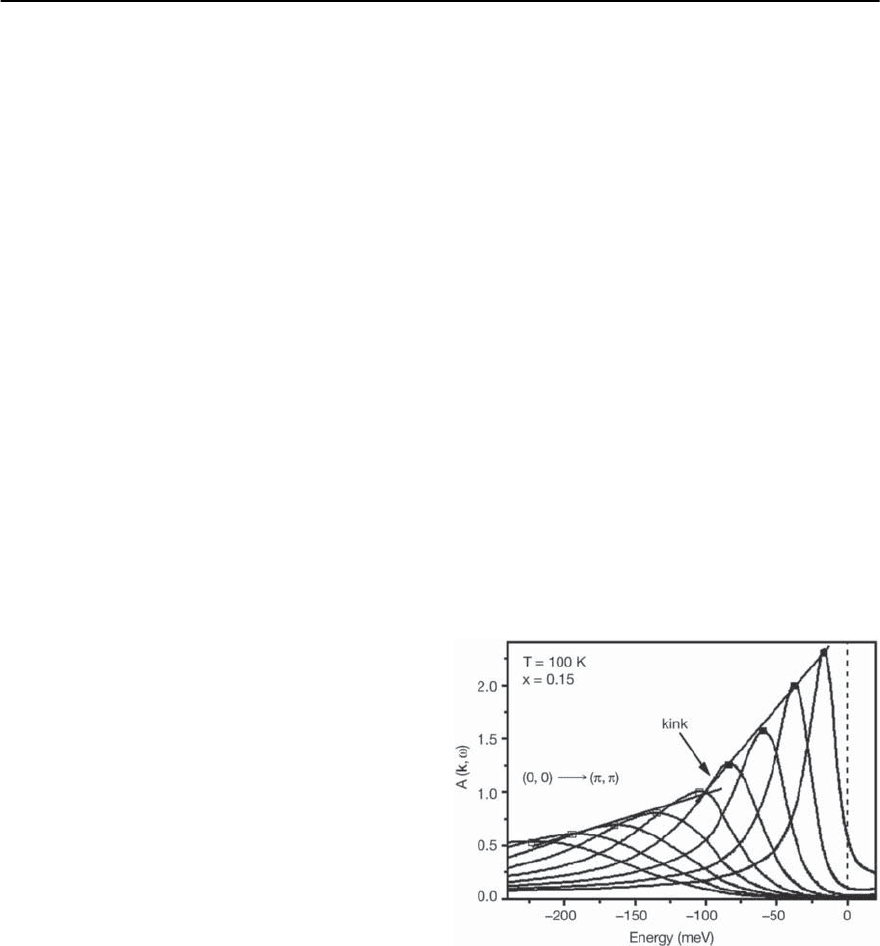
In Fig. 23.34 we show the calculated spectral den-
sity N(k, !), i.e. the local density of states, as a
function of frequency and momentum k − k
F
.The
peak positions correspond to the renormalized en-
ergy dispersion. Due to coupling of holes to antifer-
romagnetic spin fluctuations the quasiparticle dis-
persion changes its slope and shows a pronounced
kink feature at the energy !
kink
≈ 75 ± 15 meV.
How can one understand the kink feature in a sim-
ple way? At a first glance the occurrence of a kink in
the nodal direction seems to be surprising, since the
main interaction of the carriers with spin fluctua-
tions occurs at the hot spots. Note that the kink fea-
ture is present along the diagonal of the BZ close to
the cold spots. However, away from the Fermi level,
but close to it (along (0, 0) → (, )), the quasi-
Fig. 23.34. Calculated spectral density A(k, !)inthenor-
mal state along the nodal (0, 0) → (, ) direction (from
left to right) as a function of frequency in the first Bril-
louin zone.The peak positions (connected by the solid line
to guide the eye) refer to the renormalized energy disper-
sion !
k
. One clearly sees the kink structure at an energy
approximately !
kink
=75± 15 meV that results from cou-
pling of the quasiparticles to spin fluctuations
