Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

1422 D. Manske,I. Eremin, and K.H.Bennemann

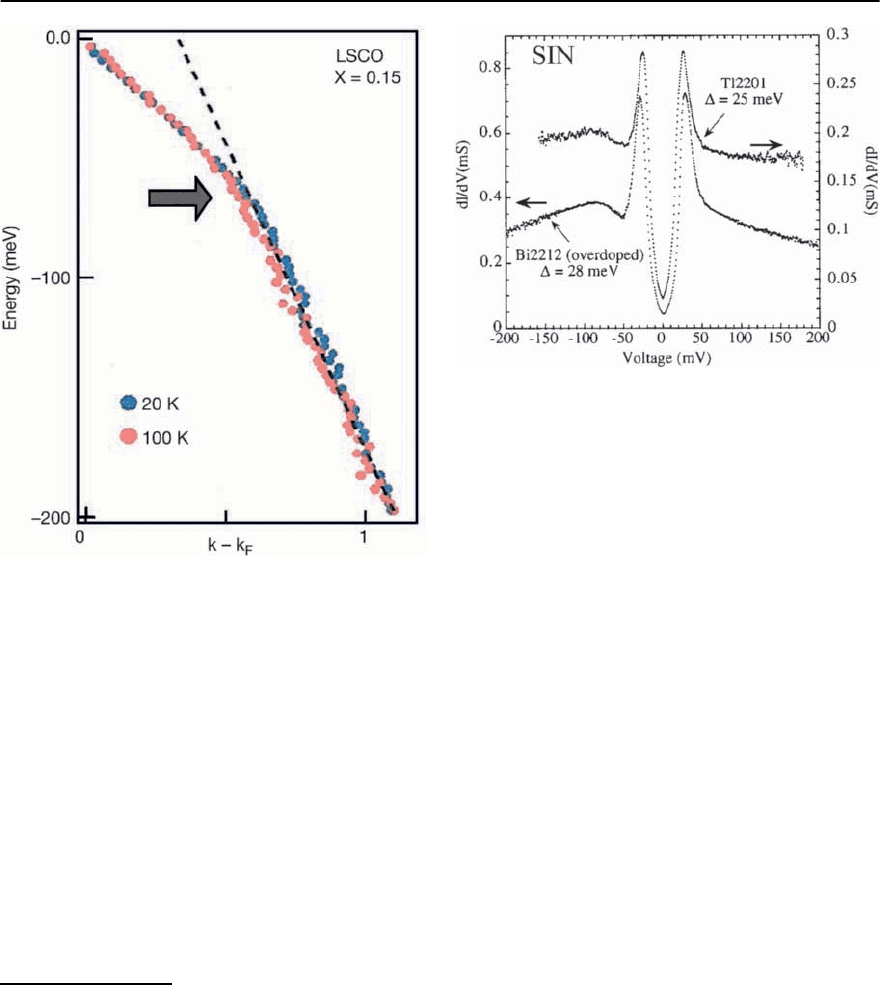
Fig. 23.8. Energy dispersion !(k − k

) in the nodal direc-

tion with respect to the Fermi energy in the first BZ as

observed byARPES for the hole-doped cuprate compound

BISSCO at different temperatures [46] vs the normalized

momentum relative to the Fermi level. Note that the slope

of the curve gives the renormalized group velocities

Brillouin zone (BZ). One clearly sees that the curve

shows a change in its slope around 50 ± 15 meV.

This so-called “kink" feature was observed by sev-

eral groups.

Note, however, that bilayer effects and

matrix elements for various incident photon ener-

gies make the spectra more complicated to analyze.

Changes in the elementary excitation spectrum due

to coupling of the carriers to spin ﬂuctuations or

other (collective) modes are generally expected. The

coupling to spin ﬂuctuations should result in rather

Fig. 23.9. Tunneling Spectra: Comparison of SIN conduc-

tances of Tl2201 and slightly overdoped Bi2212 at T =

4.2 K. The results are taken from [49]

differentfrequency and momentum dependencies of

the self-energy than in the phonon case of coupling.

To understand this “kink” feature in detail is one

of the important problems in the theory of high-T

cuprates.

Note, tunneling spectroscopy allows also to deter-

mine the structure of the elementary excitations in

cuprates. Originally, the successful analysis of tun-

neling spectra in conventional superconductors like

Pb led to the common acceptance of the electron–

phonon mechanism and Eliashberg theory of su-

perconductivity [50]. Similarly, an understanding of

the structure in the tunneling spectra in high-T

cuprates is a central problem.

In Fig. 23.9 we show results for the super-

conductor-insulator-normal metal (SIN) tunneling

conductance (dI/dV)

normalized to its normal

state value for two different cuprate superconduc-

tors, Bi

CaCu

8+ı

(BISCCO) and Tl

CuO

(Tl2201) having two and one CuO

-plane per unit

cell, respectively [49]. In both cases the supercon-

One attempted to relate the kink feature to a coupling of the itinerant carriers to phonons, in particular, to a lon-

gitudinal optical phonon mode at 60 meV, which was observed to behave anomalously in several experiments [47].

However, this interpretation has several disadvantages. The first one relates to the fact that the inelastic scattering rate

in hole-doped cuprates is linear with frequency or temperature (whichever is larger), which can be hardly explained

using conventional electron–phonon coupling. Also in electron-doped cuprates there is no kink present [48] and the

electronic part of the resistivity follows a quadratic behavior at low temperatures indicating conventional Fermi-liquid

behavior. It is not clear how both features can be explained assuming the same electron–phonon coupling.

23 Electronic Theory for Superconductivity 1423

ducting gaps and T

are demonstrating the essen-

tial independence of the observed features on the

number of CuO

-layers. Notice again the non-s-wave

character of the superconducting gap, since the tun-

neling spectra have a characteristic V-shape indicat-

ing a presence of states inside the superconducting

gap.In addition, further important details are related

to the pairing interaction. Immediately after the co-

herence peak a“dip-hump”structure is present with a

“dip”approximately at energy 3

,where

is the su-

perconducting gap at T =0.Thisstructureisasym-

metric with respect to the zero bias, since it occurs

only below T

. It is natural to suggest that the ob-

served structure results from the pairing interaction

and reﬂects the important frequency range of the

spin ﬂuctuations relevant for Cooper-pairing. One

has to understand the relation of the“dip-hump”fea-

ture to the “kink” structure seen by ARPES in order

to connect both experiments with each other.

This summarizes some key facts about super-

conductivity in hole-doped and electron-doped

cuprates. We will present an electronic theory for

the central problems by studying the interaction be-

tween carriers and spin excitations. Our theory is

able to explain basic and characteristic features in

the normal and superconducting state of cuprates

including the kink seen in ARPES and the resonance

peak observed in INS experiments.

Ruthenates

Let us describe now essential properties of Cooper-

pairing in Sr

RuO

. Superconductivity and mag-

netic activity in the ruthenates seem intimately re-

lated. The character of the magnetic activity is still

being discussed. In view of triplet Cooper-pairing

one expects that ferromagnetic spin ﬂuctuations are

present in Sr

RuO

. This is indirectly confirmed by

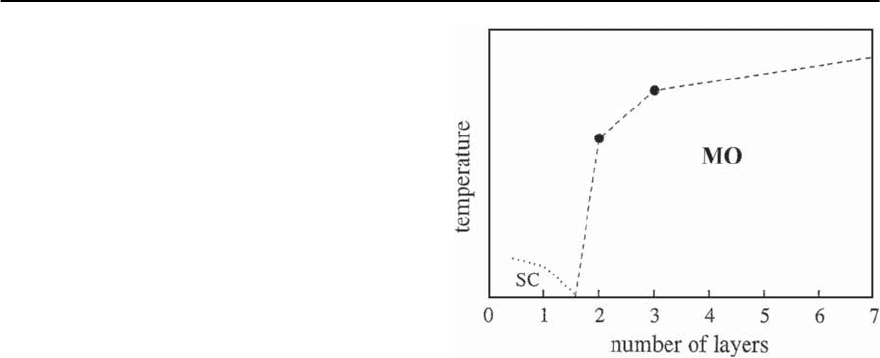
the results shown in Fig. 23.10 where we plot a

schematic phase diagram of the ferromagnetic and

superconducting members of the Ruddlesen–Popper

series (Sr

n+1

3n+1

) as a function of the num-

ber of RuO

-layers per unit cell, n.Theinfinitelayer

(SrRuO

) is a ferromagnet with T

Curie

≈ 165 K. For

n =3onefindsT

Curie

≈ 148 K and for n =2

Curie

≈ 102 K. This demonstrates the tendency that

Fig. 23.10. Schematic phase diagram of the ferromagnetic

and superconductingsystems(Rodllesen–Popper crystals)

n+1

3n+1

,taken from [51].The number of layers is the

parameter that determines the transition between the two

phases: MO = magnetically ordered and SC = supercon-

ducting

Curie

is reduced with decreasing layer number n.

This suggests that even for n = 1,when superconduc-

tivity occurs, one expects significant ferromagnetic

ﬂuctuations. These may play an important role for

superconductivity in Sr

RuO

Similar to the case of cuprates, inelastic neutron

scattering (INS) studies have revealed the formation

of strong incommensurateantiferromagnetic ﬂuctu-

ations (IAF) for the wave vector Q=(2/3, 2/3)

at energy !

= 6 meV [52] and no signature of

ferromagnetic ﬂuctuations. In addition, results for

the spin susceptibility (q, !) obtained by means

of NMR [53] indicate a remarkable temperature-

dependent magnetic anisotropy; for an illustration

see Fig. 23.11.

In general,the spin-lattice relaxation as measured

by NMR allows one to study different components

of the magnetic susceptibility like their transverse

and longitudinal parts. One finds that at room tem-

perature all components are the same. Then, for de-

creasing temperature, an isotropic response in the

ruthenates is observed.Upon coolingthe spin-lattice

relaxation starts to differ and the anisotropy reaches

a maximum at T = T

. Therefore, at low tempera-

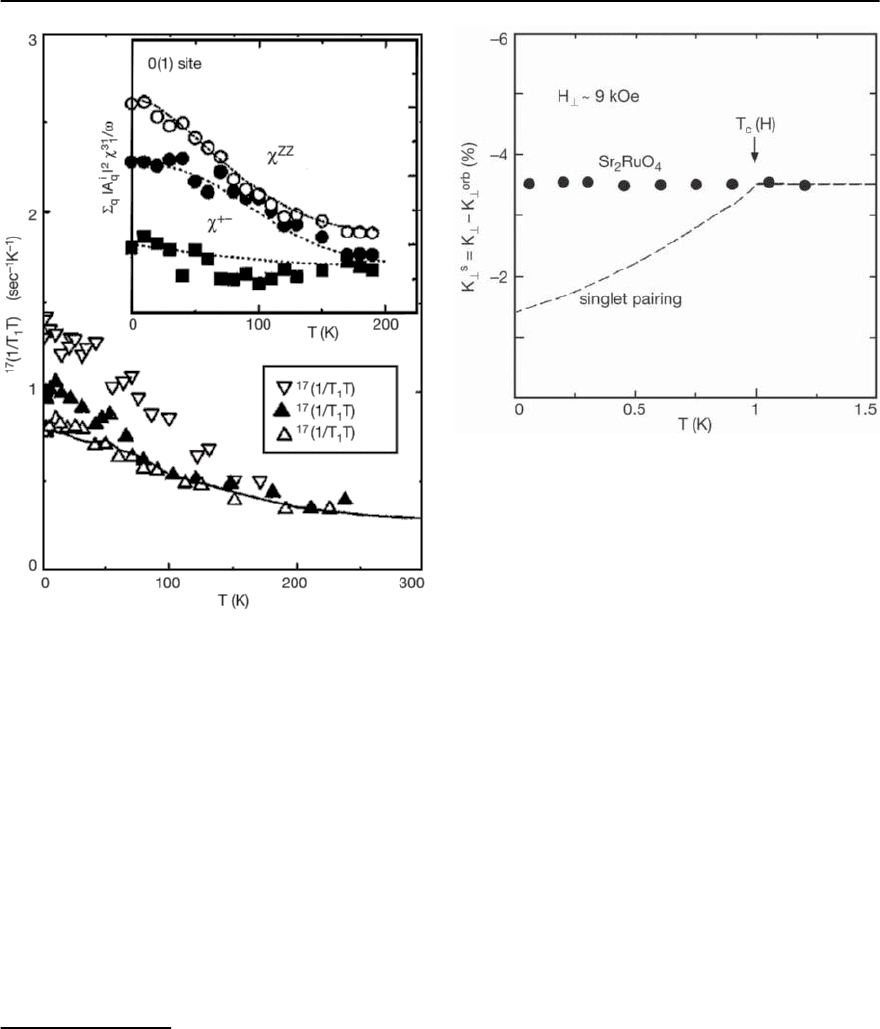
1424 D. Manske,I. Eremin, and K.H.Bennemann

Fig. 23.11. Anisotropicmagneticresponse of a single RuO

plane in the triplet superconductor Sr

RuO

vs temper-

ature as observed by NMR experiments [53]. Note that

the data are displayed only for the normal state, i.e. T ≥

=1.5 K. Results are shown for the spin-lattice relax-

ation on the oxygen nuclei

OintheRuO

-plane in terms

of (T

−1

.Intheinset the results for the corresponding

components of the spin susceptibility (transverse and lon-

gitudinal ones) are shown indicating the increase of the

magnetic anisotropy upon cooling. 

and 

+−

refer to

the response of the system to the external magnetic field

parallel and perpendicular to the RuO

-plane, respectively

tures one expects that magnetic anisotropy plays an

important role for Cooper-pairing.

What happens in the superconducting state? In

Fig. 23.12 we show experimental results suggesting

Fig. 23.12. Results for the uniform spin susceptibility,

(q =0, ! = 0) in the superconducting state of cuprates

(YBa

, dashed curve) and ruthenates measured by

NMR

Ru Knight shift [53].One can clearly see that in con-

trast to the singlet Cooper-pairing where the spin suscep-

tibilitydecreases upon cooling,theKnight shift in Sr

RuO

is unchanged by lowering T below T

.Inthecaseoftriplet

Cooper-pairing the Knight shift does note decrease below

,since the polarization induced by the external magnetic

field does not change in the superconducting state

triplet Cooper-pairing in Sr

RuO

. In conventional

superconductors the spin part of the Knight shift

measured by NMR decreases rapidly below T

due

to formation of singlet Cooper-pairs. On the other

hand, in a triplet superconductor with S =1thespin

part of the Knight shift should not change below T

since the polarization induced by the weak external

magnetic field and probed by NMR does not change.

This behavior was observed in Sr

RuO

by Ishida

et al. [53] and provides evidence for triplet Cooper-

pairing.

Note that shortly after this discovery p-wave sym-

metry of the superconducting order parameter and

triplet pairing was suggested by Sigrist and Rice [54]

Although one has to wait for further decisive and unambiguous evidence for spin-triplet Cooper-pairing from in-

plane

Oand

Ru Knight shift data, it is important to note that H

(parallel to the c-axis) is too small for NMR

measurements. Therefore, strictly speaking the present Knight shift data do not fully reinforce Sr

RuO

to be a triplet

superconductor. In order to complete the picture, further studies, for example tunneling experiments along the c-axis,

are necessary.

23 Electronic Theory for Superconductivity 1425

using a phenomenological theory and some analo-

gies between the normal state of

He and Sr

RuO

Inthecaseofp-wavepairingonehas



= 

+ ik

) , (23.4)

and thus an order parameter where || has no line

nodes. Yet it must be remarked that the microscopic

theory of triplet Cooper-pairing in Sr

RuO

is still

under discussion [55].

In general, assuming an exchange of magnetic

ﬂuctuations as responsible for Cooper-pairing like

in cuprates, the structure of the spin susceptibility

(q, !) and the Fermi surface topology should con-

trol the superconductivity in the ruthenates. Note

that ferromagnetic spin ﬂuctuations dominating

over antiferromagnetic ones will cause then triplet

paring. This is analogous to the case of triplet pair-

ing in superﬂuid

He in which p-wave symmetry is

present.

The behavior mentioned above, i.e. the magnetic

anisotropy, temperature dependence of the Knight

shift as well as of the specific heat and other prop-

erties, and of the electronic structure (Fermi surface

topology) are important characteristics of Sr

RuO

and essential for an electronic theory.

Electronic Theory

Obviously, it is of great interest to have an elec-

tronic theory explaining the important normal state

behavior and the pairing mechanism for supercon-

ductivity in cuprates and ruthenates. In this article

we present results obtained by using a Hubbard-like

model Hamiltonian and by taking into account the

coupling of the elementary excitations to spin ﬂuc-

tuations (which are partially generated by the quasi-

particles itself). This coupling may play the most

important role for Cooper-pairing. Using an effec-

tive second-order perturbation theory, the interac-

tion of the electrons (or holes) and spin ﬂuctua-

tions leads to the effective electron–electron inter-

action shown in Fig. 23.13. Applying a generalized

Eliashberg-type theory in the strong coupling limit

we describe important behavior of hole-doped and

electron-doped cuprates and Sr

RuO

.Wecompare

our results critically with experiments. Note that in

contrast to phonon-mediated superconductors no

Migdal theorem can be used [56]. In general, Trem-

blayetal.[57],andChubukovetal.[58]havestudied

the role if vertex corrections of quasiparticle cou-

ple to spin ﬂuctuations. They have pointed out that

due to !

∼ 10

−2

and a ﬂat dispersion around

(, 0) they do only change the magnitude of the ef-

fective Coulomb interaction U,butthedynamicsof

vertex corrections may be neglected (U → U

eff

Note that in the optimally and overdoped cuprates

the vertex corrections are small and have positive

sign of the Eliashberg coupling. This even enhances

the coupling to spin ﬂuctuations [59], but in un-

derdoped cuprates the vertex corrections may be-

come important. However, simply speaking, as long

as U(q, !) < 1,perturbation theory forconstruct-

ing a pairing potential in the paramagnetic phase

should work, unless poles of the bosonic mode (i.e.

in ) enhance the pair-breaking contribution of the

vertex function drastically.

Concerning the dynam-

ics, note that the pairing potential is mediated by

the same quasiparticles that form the Copper-pairs.

Therefore, one has to solve this many-body prob-

lem self-consistently. As we will discuss below, the

spin susceptibility , resulting from d-electrons of

Cu, and the gap function that is dominated by a hy-

bridization of p-electrons and d-electrons, strongly

interact with each other. Thus, in general one has

coupled equations for {G, } and {G, } where G

is the Green’s functionof the corresponding electron.

Note that in a simple spin–fermion model the feed-

back of the elementary excitations on the pairing po-

tential is neglected [58]. Simply speaking, electrons

(holes) do not only condense into Cooper-pairs, but

are also involved in the magnetic activity. Thus, a

self-consistent treatment is indeed required.

By employing the trial-and-error principle we

hope to find the correct route for a theory that may

play the same role as the BCS theory for the case of

electron–phonon interaction with s-wave symmetry

singlet Cooper-pairing. Of course, not only the dop-

If so,then the usual perturbation theory breaks down [60] and a non-perturbative approach has to be used as suggested

for example in [61].

1426 D. Manske,I. Eremin, and K.H.Bennemann

Fig. 23.13. Feynman diagram representing for the cuprates

and ruthenates the coupling of the carriers described by

Green’s function G (G

= bare propagator) to magnetic spin

ﬂuctuations described by the spin susceptibility (q, !).

U (U

eff

) is an effective (renormalized) coupling constant

that includes vertex corrections

ing dependence of superconductivity in the cuprates,

but also that of the elementary excitations and of

the spin susceptibility (q, !)areimportantprob-

lems to investigate. Cuprates and ruthenates, behave

differently due to the differences in their electronic

properties. Of course, the electronic structure, the

energy dispersions and resultant Fermi surface will

playanimportantroleasinputforthecalculations.

We will see later that in an effective one-band de-

scription of the itinerant quasiparticles the coupling

constant U (see Fig. 23.13) and a tight-binding en-

ergy dispersion will be the only parameters that enter

the theory.

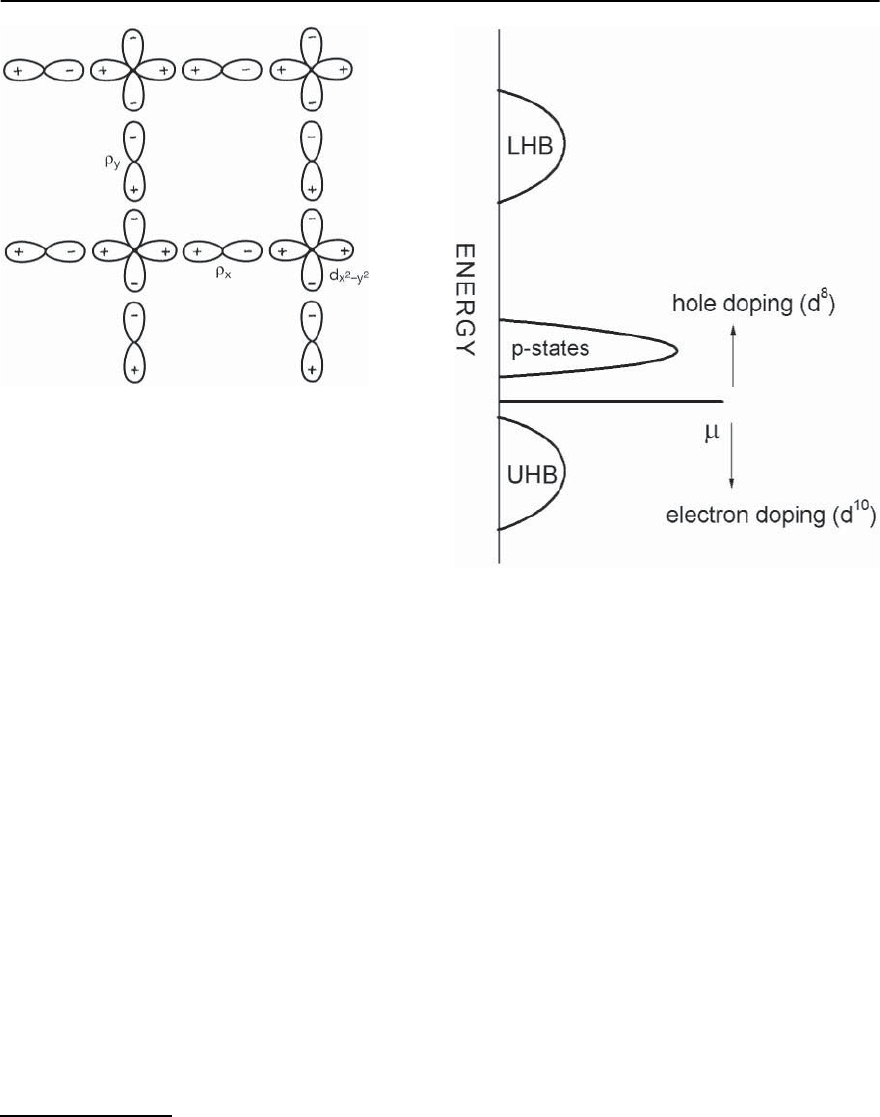
Basic Electronic Structure

For all cuprate compounds (both hole-doped and

electron-doped) the degeneracy between 3d-orbitals

is removed by the lattice structure. After some

straightforward calculations it can be shown (see

Fig. 23.14(a)) that the hybridized copper and oxygen

orbitals separate. The state with highest (lowest) en-

ergy has mainly d

−y

-wave character. The missing

electron (i.e.a hole) givesthe Cu-ion a spin

.Thus,in

the absence of doping,the cuprate material is well de-

scribed by a model of mostly localized spin-

states.

The other orbitals are occupied and therefore can be

neglected. However, the strong Coulomb repulsion

between holes in the same orbital has so far not been

taken into account and must be included.

Due to

largeCoulomb repulsion d

−y

-orbitalssplit intotwo

so-called lower and upper Hubbard bands (LHB and

UHB), respectively, as shown in Fig. 23.14(b). Then,

at half-filling the system becomes an insulator. Fur-

thermore, due to a very large U

the splitting of the

−y

-band is so large that the oxygen p-bandlies be-

tweentheUHBandtheLHB.Thechargetransfergap

in cuprates ı (ı = 

−

) is smaller than U

[62,63].

This has a very interesting consequence for the

doping of the CuO

-plane with holes or electrons.

Due to the large Coulomb repulsion the doped hole

is mainly in the oxygen p-band. Therefore, in hole-

doped cuprates the carriers (holes) occupy mainly

hybridized oxygen p-states.On the contrary,electron

doping means effective doping of the d

−y

-orbital

in UHB. Thus, the carriers in the electron-doped

cuprates sit largely at Cu 3d-sites.

Figure 23.14(b) suggests that hole-doped and

electron-doped cuprates may under certain assump-

tions be mapped on to an effective one-band Hub-

bard model. The difference between hole and elec-

tron doping will be reﬂected by the different param-

eters of the model and differences of the character

of the involved orbitals of the hybridization between

p-states and d-states. For hole doping the Fermi level

lies in the p-band and for electron doping in UHB.

The spin at Cu-sites will induce a spin polarization

at the neighboring oxygen sites upon hole doping

(see the Zhang–Rice singlet formation). This is not

thecaseforelectrondoping(atCu-sites)inwhich

a dilution of the spin system occurs. On the other

hand, in hole-doped cuprates one decreases effec-

tively only the number of Cu-spins and the system

becomesmoreitinerant.Consequently,one gets adif-

ferent behavior of (q, !) and different doping de-

pendence of antiferromagnetism in the hole-doped

and electron-doped cuprates.

Similarly as for the cuprates we use also

a Hubbard-like Hamiltonian for the ruthenates

(Sr

RuO

). However, we include three bands (˛, ˇ,

 ) crossing the Fermi-level into the calculations. In

RuO

the formal valence of the ruthenium ion is

. This leaves four electrons remaining in the 4d-

shell. Furthermore, the Ru ion sits at the center of

Actually neglecting interactions, one would have expected La

CuO

to be metallic with a half-filled conduction band.

As we know this is not true and this material is an antiferromagnetic insulator. Therefore, double occupancy should be

energetically not favorable due to Coulomb repulsion.

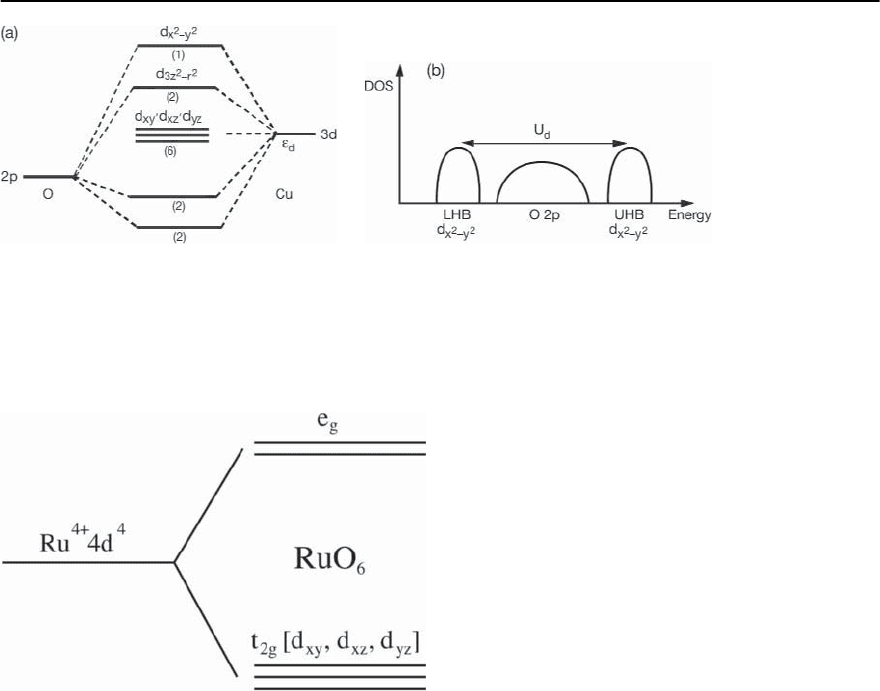
23 Electronic Theory for Superconductivity 1427

Fig. 23.14. SchematicelectronicstructureofCuO

-planes reﬂecting bonding between a Cu

and two O

2−

ions. (a)Initial

splitting of the bands taking into account crystal field interaction only.We consider only d-electrons (holes) of Cu and p

and p

orbitals of the oxygen. The numbers indicate the occupations of the different levels in the undoped compound.(b)

Roleof the on-site Coulomb repulsion and the splittingof the 3d

−y

2 -orbital into a lower (LHB) and upper Hubbard band

(UHB).U

is the Coulomb repulsion between electrons at Copper.Due to ı = 

−

< U

the cuprates are Mott–Hubbard

insulators without doping

Fig. 23.15. Electronic structure of Sr

RuO

.TheRu

ion

corresponds to a 4d

level. The splitting of the e

and t

subshells is due to the RuO

crystal field. The orbitals d

,andd

cross the Fermi level.Magnetic activity results

from the t

subshell. The RuO

-plane structure plays an

important role

aRuO

-octahedron and the crystal field of the O

2−

ions splits the five 4d-states into threefold (t

)and

twofold (e

) subshells as illustrated in Fig. 23.15. The

negative charge of the O

2−

ions causes the t

sub-

shell to lie lower in energy. Note that these orbitals

(xz, yz,andxy) have lobes that point between the

2−

ions lying along the x, y,andz-axes. Electrons

of these orbitals form the Fermi surface and as we

have already mentioned the ˛, ˇ,and -bands. We

again assume that the most important interaction of

the carriers is with spin excitations described by the

spin susceptibility (q, !) and resulting from Ru ˛,

ˇ,and -states.

To explain the experimentally observed large

anisotropy of the magnetic activity in the RuO

plane, see 

+−

(q, !)and

(q, !) along the z-

direction perpendicular to the planes, we include

also spin–orbit coupling for the significant ˛, ˇ,

and  -bands.Again,we hope that our trial-and-error

type philosophy and critical comparison with exper-

iments will help us to find the correcttheory and will

explain triplet superconductivity.

Summary

In summary, by using a Hubbard-like Hamiltonian

we attempt to describe the electronic properties

of the layered superconductors Cu-oxides and Ru-

oxides. The theory for spin excitation-mediated su-

perconductivity in cuprates and ruthenates may also

help us to find a theory for the other novel supercon-

ductors such as the heavy-fermion ones, ZrZn

,UPt

UGe

,etc.

In the next sections we describe the electronic the-

ory for calculating (a) the elementary excitations,the

self-energy and spectral density; (b) the spin suscep-

tibility (q, !); and (c) superconductivity and the

symmetry of the superconducting order parameter.

We present results for various important properties.

Finally,we discuss the limitationof our model forthe

cuprates and ruthenates and give an outlook.

1428 D. Manske,I. Eremin, and K.H.Bennemann

23.2 Electronic Theory for H ole-Doped

and Electron-Doped Cuprates

We present now the theory for the interaction be-

tween quasiparticles and spin ﬂuctuations in the

cuprates and in Sr

RuO

. For simplicity we assume

that the electronic dynamics is controlled by the

CuO

and RuO

-planes, respectively.

For the description of singlet superconductivity

in the cuprates we use a one-band model Hamilto-

nian.The interaction between the carriers (quasipar-

ticles) is described by an effective Coulomb coupling

U and the itinerancy of the carriers by a hopping in-

tegral t.We assume that these can be describedby the

effective one-band with U. In the case of hole dop-

ing the states of the effective band are mainly the

p-states originatingfrom O-atoms. The spin ﬂuctua-

tionsarisefromthe magnetic activity oftheCu-spins

and the induced spin polarization of the p-states. In

the case of electron doping the effective one-band

Hamiltonian describes the hybridized d-states of the

UHB(seeFig.23.14(b)) andU is an effective coupling

between the electrons in these states. The spin ﬂuc-

tuations result from the Cu-spins. Upon doping the

Cu-spins are quenched and the spin polarization of

the band is reduced.We assume itinerant magnetism

for the UHB. We will see later from a comparison of

the theoretical results with experiments in the opti-

mally and overdoped case that this is a useful model.

For describing Cooper-pairing in Sr

RuO

also employ a Hubbard Hamiltonian. In contrast to

cuprates no doping occurs. In order to derive an elec-

tronic theory it is important to take the electronic

band structure of the t

-subshell into account and

thus to include the states of the d

, d

,andd

bands that cross the Fermi level. Magnetic activity

arises from itinerant electrons in the Ru d-orbitals.

Due to a different topology of the corresponding

Fermi surfaces a strong magnetic anisotropy occurs

(

+−

> 

) in the normal state. This mainly results

from different values of the g-factor for the trans-

verse and longitudinal components of the spin sus-

ceptibility (i.e. the matrix elements differ) and from

a change of the bare energy dispersion of the d-

electrons. Obviously,this will have consequences for

the symmetry of the superconducting order param-

eter. In order to describe this magnetic anisotropy,

one must also take into account spin–orbit coupling.

23.2.1 Electronic Structure and the Hamiltonian

In the case of the cuprates the calculation of the elec-

tronic properties is complicated due to strong elec-

tronic correlations.

In order to account for these we

use a simplifying model that includes the states orig-

inating from the CuO

-planes and play the most sig-

nificant role. First, we neglect interlayer coupling of

CuO

-planes.

In Fig. 23.16 we show the electronic structure of

aCuO

-plane. The undoped case corresponds to a

half-filled band, i.e. one hole per copper site. The

holes mainly occupy the d

−y

-orbitals and interact

with each other via superexchange yielding an anti-

ferromagnetic ground state. Due to a large Coulomb

repulsion U = U

further holes that are doped into

the CuO

-plane are mainly placed on the four oxygen

p-states surrounding the copper sites. Thus, the cen-

ter of mass of these new quasiparticles is still located

on the copper sites. Obviously, the spin polarization

of the doped holes tends to suppress the antiferro-

magnetism. In addition, spin frustration takes place

for small hole-doping.

In the case of electron-doped cuprates the doped

carriers directly occupy copper d

−y

-states. There-

fore, the antiferromagnetism is weakened by diluting

the copper spins. No spin frustration occurs.

Finally, after doping a reasonable number of car-

riers into a CuO

-plane, in both cases, electron or

hole doping, one ends up with a non-ordered para-

magnetic (metallic) phase that still reveals (short-

range) antiferromagnetic correlations. The resulting

spin excitations are responsible for singlet Cooper-

As we know from the experiment the parent cuprate compounds are antiferromagnetic insulators.At the same time by

applying a local-density-approximation calculation on undoped cuprates one finds that the system should be metallic

with one hole per unit cell that satisfies the formal valencies of La

2−

,andCu

[64] that is inconsistent with

experiment.The neglection of the electronic correlations due to strong local Coulomb repulsion is responsiblefor this.

23 Electronic Theory for Superconductivity 1429

Fig. 23.16. Schematic representation of the electronic struc-

ture of a single CuO

-plane consistingof Cu d

−y

2 -orbitals

and the oxygen p



-orbitals. Without doping one hole is

present in the Cu d

−y

2 -orbital.Via hybridization with oxy-

gen (i.e.superexchange) p-orbitals of two neighboring cop-

per holes interact antiferromagnetically. This leads to an-

tiferromagnetic ordering of the Cu-spins. The doped holes

are mainly in the oxygen p-orbitals due to a large Coulomb

repulsion U = U

and destroy antiferromagnetism of the

copper spins and spin frustration occurs. In contrast to

this, doping the CuO

-plane with electrons means effec-

tively occupation of the UHB band and dilution of the

Cu-spins and thus weakening of the antiferromagnetism

pairing in the cuprates. In our electronic theory we

assume that these can be described mainly by itiner-

ant carriers.

We start by using the three-band Hubbard-like

model [65]

H = 



i,

i

+ 



i,

i

(23.5)



i,j,



i

j

+h.c





i,j,



i

j

+h.c



+ U



i↑

i↓

+ U



i↑

i↓

+ U



i,j

i↑

j↓

for describing the hole-doped and electron-doped

cuprates.Here,the sums are performed over the cop-

per and oxygen lattice positions both labeled by i

Fig. 23.17. Illustration of the hole and electron doping in

cuprates. Without doping due to strong electronic correla-

tions the chemical potential  lies between the upper Hub-

bard band (UHB) of the copper d

−y

2 -orbital and oxygen

p-states. Upon hole doping the chemical potential shifts

towards the oxygen p-band leading to an insulator–metal

transition. In the case of electron doping the chemical po-

tential lies in the copper UHB.Notethat the lower Hubbard

band (LHB) of d

−y

2 -states is separated largely in energy

from the oxygen p-states due to U

 ı, ı = 

− 

and  refers to the spin.t

˛ˇ

describes the hopping be-

tween the sites i and j and states ˛ and ˇ.n

i

= d

i

and n

i

= p

i

are the Cu 3d and O 2p hole densi-

ties for site i, respectively. U

and U

refer to on-site

copper and oxygen Coulomb repulsion, respectively,

and U

accounts for the copper–oxygen interaction.

As we have discussed above, due to strong elec-

tronic correlations the undoped cuprates are an-

tiferromagnetic insulators. The chemical potential

lies between the upper Hubbard band of the d

−y

orbitaland oxygen p-band (see Fig.23.17 for an illus-

We assume that the Cu-spins are part of the p − d hybridized states.

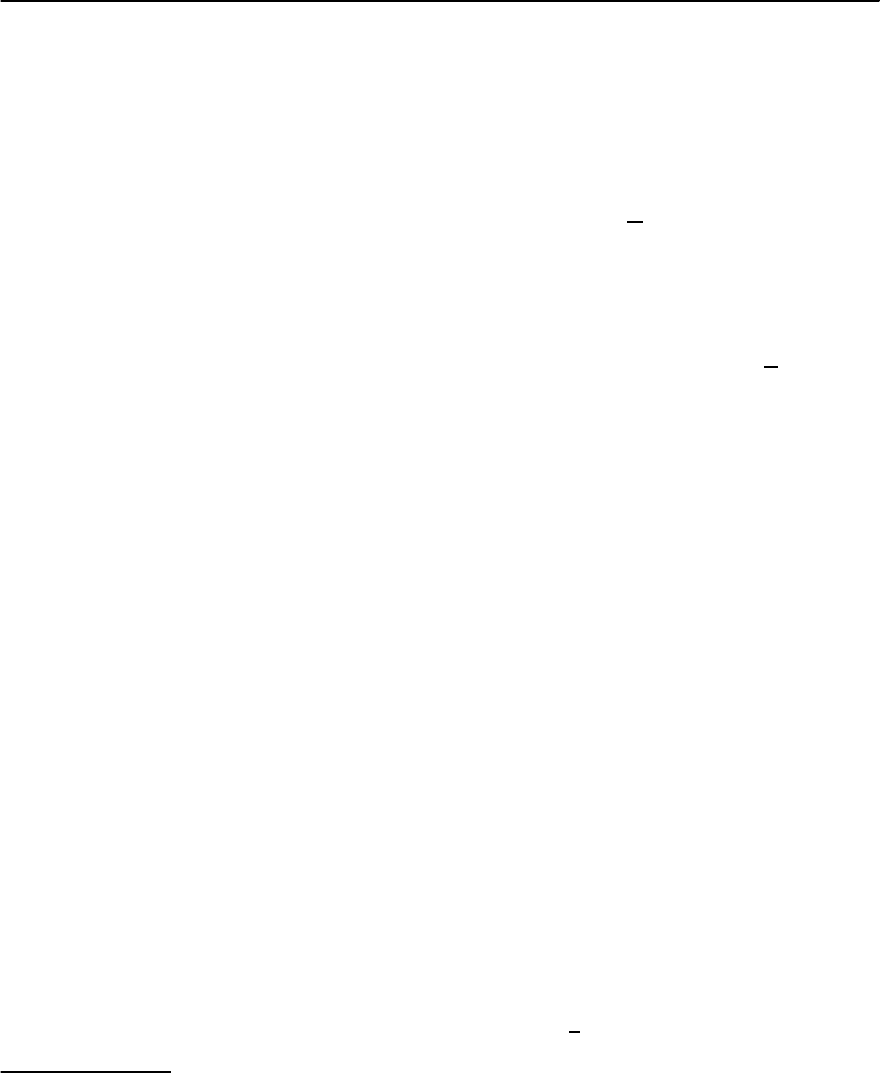
1430 D. Manske,I. Eremin, and K.H.Bennemann

tration).Uponhole dopingthe chemicalpotentiallies

in the oxygen p-band. The latter hybridizes strongly

with copper d-states. As a result the bandwidth of

the oxygen band reduces and Zhang–Rice singlets

are formed [66]. In the case of electron doping, the

chemical potential lies in the copper upper Hubbard

band (UHB). Furthermore, due to large values of U

andof thecharge-transfer gap ı,thecopperUHBand

LHB are well separated in energy. This suggests the

use of an effective one-band Hubbard-like Hamilto-

nian

for doped cuprates:

H =−



i,j



i

j

+h.c.



+ U



i↑

i↓

+ ...

(23.6)

describing the dynamics of holes in hybridized p-

states and of electrons in effective d-states of the

UHB. In (23.6) the c

i

are fermion creation opera-

tors for spin  on sites i of a two-dimensional square

lattice, and n

i

= c

i

denotes the density for spin

 . The Hubbard U describes the effective Coulomb

interaction between the quasiparticles in the con-

duction band and thus should be a good description

of the paramagnetic state with strong antiferrromag-

netic correlations.

Note that the effective interaction U might be dif-

ferent in hole-doped and electron-doped cuprates.

In the latter case both itinerant behavior and mag-

netism result from the electrons in the copper d-

states of the UHB. In the hole-doped case the hole

carriers are located mainly on the oxygen p-states,

and the magnetic activity arises mainly from Cu-

spins, the localized copper d-holes. These interact

with the spins of the doped holes that are present at

the oxygen sites. In (23.6) the interaction of the itin-

erant electrons with the Cu-spins results from U and

the remaining not explicitly given terms take care of

the local spin character. Note that the interaction of

local spins S

with itinerant carriers having spin 

should be of the form (S

·  ). For simplicity one is

tempted to simulate this in the case of hole doping

by an effective interaction between the band elec-

trons (holes).Consequently the dots in (23.6) refer to

residual interactions, for example resulting from the

local character of the Cu-spins.

Using this physical picture we develop the Eliash-

berg theory for Cooper-pairing in hole-doped and

electron-doped cuprates. First, we rewrite the effec-

tive one-bandHubbard Hamiltonian for the itinerant

carriers in momentum space:

H =



k



†

k,





q

†

k,

†



,−



+q,−

k−q,

(23.7)

with the one-band electron (or hole) energy



=−2t



cos(k

)+cos(k

)

−2t



cos(k

)cos(k





. (23.8)

From now on the coupling constant U denotes an ef-

fective interaction for the carriers in the p − d-states

including largely the effects due to (S

·  ). For a de-

scription of the itinerant quasiparticles we assume

nearest neighbor and next nearest neighbor hopping

described by t and t



, respectively. Here and in the

following we set the lattice constant equal to one.

Note that the general form of the unrenormalized

tight-binding energy dispersion is the same for holes

and electrons,but with different parameters used for

t and t



. These have to be chosen in agreement with

the experimentally observed Fermi surface in hole-

doped and electron-doped cuprates.

23.2.2 Eliashberg Theory for the Interaction Between

Quasiparticles and Antiferromagnetic Spin

Fluctuations

In general, the interaction between the carriers and

spin ﬂuctuations in the cuprates is given by

int



eff

(q)

−→

s (q)

−→

S (−q) . (23.9)

Here,

eff

denotes the effective coupling and s(q)is

the spin operator of the itinerant carriers,

−→

s (q)=







k+q,







k,



, (23.10)

Note, the validity of the effective one-band Hamiltonian for the hole-doped cuprates has been also justified from a

microscopic consideration of Baumg¨artel, Schmalian and Bennemann [67] on the basis of p − d Hamiltonian using a

slave-boson technique [68].

23 Electronic Theory for Superconductivity 1431

where represents the Pauli matrices.S(Q)isthespin

operator referring to the Cu-spins. The correspond-

ing spin–spin correlation function gives the dynam-

ical spin susceptibility,(q, !). Due to itinerancy of

the Cu spin electrons the susceptibility may be de-

terminedby therandomphase approximation (RPA).

Then,



RPA

(q, !)=



(q, !)

1−

U

(q, !)

. (23.11)

Here, 

is the bare spin susceptibility which is de-

fined via retarded Green’s functions for the quasipar-

ticles creating the spin excitation. Then, in second-

order perturbation theory the effective interaction

between carriers has the form (see Fig. 23.13):

eff



RPA

(q, !)

U , (23.12)

where

eff

and

U refer to the coupling between

the carriers and the spin excitations. The Hubbard-

like interaction

eff

includes vertex corrections

whereas

U denotes the effective coupling. Then, the

Eliashberg-like system of equations for a supercon-

ductor are given by the Green’s function (G

−1

− £) with self-energy:

£(k, !)=

eff











RPA

(k − k



, ! − !



)

× G(k



, !



) (23.13)

and anomalous self-energy

¥ (k, !)=−

eff











RPA

(k − k



, ! − !



)

× G(k



, !



) G(−k



, −!



)¥ (k



, !



) . (23.14)

Here, £(k, !) is the self-energy of the one-particle

Green’s function G(k, !) in the normal state and

¥ (k, !)=(k, !)Z(k, !) is the corresponding

anomalous part. The superconducting order param-

eter is (k, !). Z(k, !) denotes the renormalization

function describing the effective mass of the quasi-

particles. We employ the Dyson equation yielding

G(k, !)=

! − 

+  − £(k, !)

≡ G(k) . (23.15)

This system of equations allowsone to find the super-

conducting gap and the superconducting transition

temperature T

(defined throughafiniteoff-diagonal

self-energy,i.e.(T < T

) = 0).The spin ﬂuctuations

and (q, !)wouldactasaninput.

Note that on the RPA level also the charge ﬂuc-

tuations are included. This may be of interest if a

charge-density-wave (CDW) or stripe formation oc-

curs. Both may compete for small doping. The su-

perposition of spin and charge ﬂuctuations leads to

 = 

+ 

with



RPA

(q, !)=



(q, !)

U

(q, !)

. (23.16)

Then, in the Nambu representation [69] the 2 × 2

matrix £(k) is given by the expression

£(k)=





(k − k



) 

G(k



) 





(k − k



) 

G(k



) 

, (23.17)

where 

(˛ =0, 1, 2, 3) are the Pauli matrices and

and V

are the matrix elements of the electron–

electron interaction due to spin and charge ﬂuctua-

tions shown in Fig.23.18.Omittingthe firstdiagram,

since it yields a shift in thechemical potential  (non-

retarded) and has no d-wave contribution, one finds

(q)=

eff

U 

(q),

(q)=

eff

U 

(q) , (23.18)

where 

and 

are the dynamical spin and charge

(dielectric) susceptibilities which within RPA are

given by



(q)=



(q)

1−

U

(q)



(q)=



(q)

U

(q)

. (23.19)

Here, 

(q)and

(q) are the corresponding ir-

reducible parts calculated from unrenormalized

Green’s functions

,i.e.

∼



(k)G

(k + q).

Note that including charge ﬂuctuations effects might be of interest in connection with lattice distortions and stripe

formation. Superconductivity and charge density wave formation may coexist to some extent in the cuprates.