Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

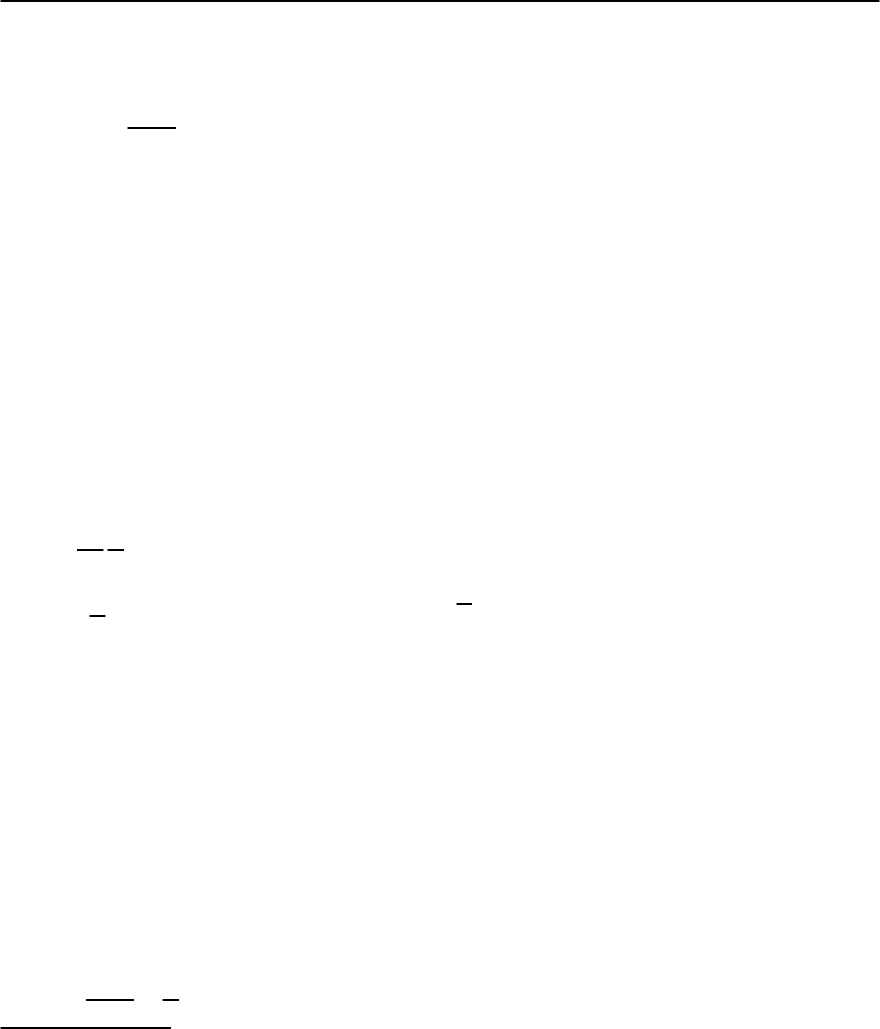
1442 D. Manske,I. Eremin, and K.H.Bennemann

where we have introduced for convenience the oscil-

lator strength



2e

∞





(!)d! . (23.52)

is the corresponding value of (23.52) in the super-

conducting state. In (23.52) we have used the f -sum

rule for the real part of the conductivity 

(!)

∞





(!)d! = e

n/2m

∗

where n is the 3D hole density and m

∗

denotes the ef-

fective band mass (in our case for the tight-binding

band considered). The conductivity (!)thaten-

ters the equations above is calculated in the nor-

mal and superconducting state using the Kubo for-

mula [73,80]



(

)

c



∞



−∞





f (!



)−f (!



+ !)







k,x

+ v

k,y



(23.53)



N(k, !



+ !) N(k, !



(k, !



+ !) A

(k, !



)



Here,v

k,i

= ∂

/∂k

arethe calculatedbandvelocities

within the CuO

-plane and c is the c-axis lattice con-

stant.The spectral functionsN and A

are defined in

(23.168).Vertex correctionshave been neglected.

Physically speaking, we are looking for the loss

of spectral weight of the Drude peak at ! =0that

corresponds to excited quasiparticles above the su-

perconducting condensate for temperatures T < T

∗

Then, with the help of above equations we calculate

the dynamical conductivity (!)via(e =elemen-

tary charge) [73]

(!)

! Im  (!) , (23.54)

where Im  (!) has been obtained using (23.54)

from the current–current correlation function and

the Kubo formula. In a next step the penetration

depth (x, T) is calculated within the London the-

ory [81] by



−2

∝ n

This will be discussed later.

Of course, in particular for underdoped cuprates

phase ﬂuctuations of the Cooper-pairs must be in-

cluded into the calculation of n

. A generalization of

(23.54) leads to

(q, !)=! Im  (q, !) . (23.55)

(Note that the derivation requires Fermi-liquid-like

argumentsassuming a thermodynamical phase tran-

sition which might not be valid if the limit T → 0

in the vicinity of a quantum critical point (QCP) is

considered. This will be discussed in Sect. 23.4.7.)

Since the conductivity  can be expressed in terms

of a current–current correlation function, n

is re-

lated to J(r, t)·J(0, 0),whereJ ∝



∗

∇ − ∇

∗



Using (r, t)=| |e

i(r,t)

one arrives at (∇(0, 0) =

c

−→

A (0, 0) for frozen amplitude ﬂuctuations,see Ap-

pendix D.)

∼∇(r, t) ·∇(0, 0). (23.56)

On general grounds one expects that the phase cor-

relation function C = ∇ ·∇



behaves as C → 1

for large doping x and that a Meissner effect occurs

only for C(T) → 1atT

(Here, ∇ ·∇



means

phase averaging).

From this we can calculate n

(q, !) and its doping

dependence. For overdoped cuprates and for T → 0

we expect that phase ﬂuctuations play a minor role,

the see detailed discussion in the next section, while

for underdoped cuprates (x → 0) Cooper-pair phase

ﬂuctuations should become more and more impor-

tant. However, for frequencies ! ∼ 1/time > !

phase

the behavior of n

(q, !)shouldcorrespondtothe

In analogy to ferromagnetism like in Ni we expect n

= ∇¥ (r, t)∇¥ (0).Notethatitisstraightforwardtomap

our electronic theory on a lattice (Wannier type representation) and then to derive from the product of the anomalous

Green’s functions, {F · F

∗

}, a contribution to the free energy of the form n

cos Ÿ

as used by Chakraverty et al. [78].

Here, Ÿ

is the angle between the phase of neighboring Cooper-pairs. Approximately, one has n

= n

,with

for T < T

and

=0forT > T

23 Electronic Theory for Superconductivity 1443

case where no phase ﬂuctuations are seen. In this

connection !

−1

phase

= 

refers to the lifetime of the

phase ﬂuctuations. In underdoped cuprates it de-

scribes the dynamics of n

.Weestimatethelifetime

from 

∝ 

−1

∝ T

−1

, since the energy change

involved in the excitations is of the order of e

i

Note that above T

one has e

i

 = 0 due to phase-

incoherent Cooper-pairs.

In summary, our mean field results for n

(x, T)

areexpectedtobeapproximatelyvalidforoverdoped

cuprates and also for underdoped cuprates if T → 0

for times shorter than the lifetime of the phase ﬂuc-

tuations. If Cooper-pair phase ﬂuctuations become

important the superﬂuid density is given by (23.56).

Note that for q → 0,! → 0 after phase averaging of

∇(r, t)·∇(0, 0)→0 onearrivesat T = T

.Thus,

the Meissner effect occurs only for phase-coherent

Cooper-pairs.In the following we safely approximate

the phase correlation function ∇ ·∇≈0above

.BelowT

one takes ∇∇≈1 for simplicity.

This is approximately true for Gaussian ﬂuctuations.

23.2.7 Cooper-Pair P h ase Fluctuations

As mentioned above the cuprates consist of weakly

coupled two-dimensional CuO

planes. For doping

x → 0 the Cooper-pairs do not overlap much.There-

fore, one expects that Cooper-pair phase ﬂuctuations

are enhanced. These ﬂuctuations of phase incoher-

ent Cooper-pairs destroy the long-range supercon-

ducting order and the Meissner effect. In conven-

tional bulk superconductors Cooper-pair phase ﬂuc-

tuations are not relevant, since the large superﬂuid

density leads to a strong overlap of Cooper-pairs and

the phase ﬂuctuations cost much energy. Thus, in

conventional superconductors the superconducting

transition is due to the destruction of the Cooper-

pairs and T

is proportional to 

[76]. On the other

hand,the observationbyUemura et al.that T

∝ n

underdoped hole-doped cuprates [14] indicates that

the phase ﬂuctuations drive the transition in these

regime. Then, at T → T

where F

phase

 T

phase

coherent Cooper-pairs occur. F

phase

denotes the

free energy contribution due to phase ﬂuctuations.

Cooper-pairs might exist above T

and break only up

at a crossover temperature around T

∗

> T

. Here, T

∗

Fig. 23.23. Illustration of the significance of Cooper-pair

phase ﬂuctuations in underdoped cuprates with low super-

ﬂuid density n

.With the help of the generalized Eliashberg

theory below the crossover temperature T

∗

one finds local

Cooper-pairs without long-range phase coherence (“pre-

formed pairs”). The temperature T

denotes the supercon-

ducting phase transition temperature below which phase

coherent Cooper-pairs and the Meissner effect occur. For

x < x

opt

one gets T

∗

→ T

due to phase ﬂuctuations

is approximately given by the transition temperature

that one would obtain without phase ﬂuctuations.

Note that the Meissner effect takes place only below

. This situation is illustrated in Fig. 23.23.

The bulk transition temperature T

at which

phase coherence of the Cooper-pairs occurs is de-

termined by the Ginzburg–Landau free energy func-

tional F{n

, } where the superﬂuid density di-

vided by the effective mass m, n

(x, T)/m,iscal-

culated self-consistently from the current–current

correlation function. First, we consider the static

case, i.e. n

= n

(!). The doping dependence of

the Ginzburg–Landau-like free-energy change (see

(x, T)) is given by

F = F

− F

=−





D

†

D e

−



eff

[

†

,]



(23.57)

The functional integral is taken over the fields D

†

d

†

, t

). The effective action S

eff

is defined

in Appendix D where we also derive the Dyson equa-

tion for the Cooper-pair phase ﬂuctuations on a mi-

croscopic level. On phenomenological grounds the

1444 D. Manske,I. Eremin, and K.H.Bennemann

Gor’kov equations including the phase ﬂuctuations

were derived by Berthod and Giovannini [82]. Equa-

tion (23.57) is the basis for determining T

in the

presence of Cooper-pair phase ﬂuctuations. For sim-

plicity, we neglect first the interaction between the

amplitude and the phase of Cooper-pairs (see foot-

note on page 1442 and Appendix D for details of

the interplay between amplitude and phase ﬂuctua-

tions).Then, we write

F = F

cond

+ F

phase

, (23.58)

where F

cond

≈ ˛{n

∗

}

(x) is the condensation

energy due to Cooper-pairing and F

phase

≈



∗

the loss in energy due to phase incoherent Cooper-

pairs. Here, ˛ denotes the available phase space for

Cooper-pairs normalized per unit volume and can

be estimated in strongly overdoped regime. In con-

trast to conventional superconductors in cuprates

˛ is smaller mainly due to large size of the unit

cell [83–85]. This will be discussed later in connec-

tion with Fig. 23.52.

From the interplay between condensation energy

and phase ﬂuctuation energy we can estimatethe role

of phase ﬂuctuations for determining T

at different

doping. One expects that for underdoped cuprates

0.15 > x → 0, phase ﬂuctuations get more impor-

tant and cost less energy. Thus F

phase

< F

cond

and

consequently T

∼ F

phase

< F

cond

∼ T

∗

.Note

that Cooper-pairs break up thermally at T

∗

. Since

F

phase

∝ n

one gets due to Cooper-pair phase ﬂuc-

tuations T

(x) ∝ n

(x) in the underdoped regime.

In the overdoped case the situation is described by

the fact that Cooper-pair phase ﬂuctuations cost too

much energy. Consequently, the system undergoes a

mean-field transition according to a gain in conden-

sation energy F

cond

and then T

(x) ∝ 

(x). Note

that the explicit derivation of the free-energy func-

tional is given in Appendix D. The Meissner effect

only occurs if after phase averaging n

(! → 0) =0

yielding a London penetration depth



(T)

∝ n

(T, ! =0).

Here, n

refers to the phase averaged superﬂuid den-

sity. Within standard (time-dependent) Ginzburg–

Landau theory (see footnote on page 1442), the su-

perﬂuid density n

can be calculated through (23.56).

To summarize, using this physical picture one al-

ready obtains on general grounds a superconducting

phase diagram and in particular an optimum T

and

doping concentration as it is illustrated in Fig. 23.23.

In particular, calculating F

cond

and F

phase

from

the generalized Eliashberg equations one finds an

optimal doping concentration at x

opt

 0.15. We

get T

∝ F

cond

∼ 

for overdoped cuprates and

∝ F

phase

∼ n

for underdoped cuprates. Clearly,

the Meissner effect occurs only for phase coherent

Cooper-pairing and 

−2

∝ n

BKT Theory for Cooper-Pair Phase Fluctuations

Due to the layered structure of the cuprates and

weak interlayer coupling the underdoped cuprates

should behave in accordance with the 2D-XY model

(except in a narrow critical range around T

where

3D-XY is more appropriate) [86,87].Thus, the stan-

dard theory for the 2D-XY model, the Berezinskii–

Kosterlitz–Thouless (BKT) renormalization group

theory, should be a reasonable starting point for a

study of Cooper-pair phase ﬂuctuations [88–91]. In

particular we discuss the determination of T

with

the help of the BKT theory similar to the work by

Timm et al. [92].

The superconductingtransition predicted by BKT

theory is due to unbinding of ﬂuctuating vortex–

antivortex pairs in the superconducting order pa-

rameter. Gaussian phase ﬂuctuations are not im-

portant, since they do not shift T

. (This is true in

three dimensions. Of course, in the 2D case Gaus-

sian ﬂuctuations destroy the long-range order yield-

ing T

= 0, but the mean-field transition is still un-

changed.) Since we are mainly interested in the de-

termination of T

, we first consider the static case

where the phase  does not depend on frequency.

Then, the phase action is given by

phase



r (∇)

, (23.59)

where the phase stiffness is related to the super-

ﬂuid density through

K = n

(T)

/(4m

∗

T). For

23 Electronic Theory for Superconductivity 1445

the cuprates it turns out that the relevant parame-

ters for the unbinding of thermally created vortex–

antivortex pairs are the dimensionless stiffness K

and the vortex core energy E

core

. The vortex core en-

ergy refers to the energy amount that is needed for

the suppression of the superconducting order pa-

rameter in the vortex core, i.e. (r → r

core

)=0.

This, in general will renormalize the phase stiffness

yielding K → K

. The stiffness is related to n

K(T)=ˇ

(T)

∗

, (23.60)

where ˇ denotes again the inverse temperature and

m is again the effective mass.d is the average spacing

between CuO

layers. In our calculations we set d to

half the height of the unit cell of YBa

6+x

, see,

forexample [92].Notethatthe renormalizedstiffness

is related to the superﬂuid velocity through





r v

(r) · v

(0). (23.61)

For determining T

one has to solve the Kosterlitz

recursion relations (“ﬂow equations”) [88,92]

(

2−K

)

y (23.62)

and

=−4

. (23.63)

Here, y = e

−ˇE

denotes the vortex fugacity. For the

vortex core energy we use the approximate result by

Blatter et al., i.e. [87]

core

= k

TK ln  , (23.64)

where is the Ginzburg parameter.l =(r/r

)isalog-

arithmic length scale which relates K to the strength

of the vortex–antivortex interaction. Note that for

T > T

, K tends to zero for l →∞. The interaction

at large distances is screened and the largest vortex–

antivortex pair unbind. This destroys the Meissner

effect and leads to dissipation. On the other hand,

bound Cooper-pairs reduce K and thus n

,butdo

not destroy superconductivity.After solving (23.62)-

(23.64) it turns out that the renormalization of K

is very small [92]. Thus, within a good approxima-

tion,Timm et al. obtain T

(x)fromthesimplecrite-

rion [88,92–94]

K(T



, (23.65)

, x)

∗





. (23.66)

The superﬂuid density n

(T, x) entering (23.66) is

calculated from the generalized Eliashberg equations

using (23.56)–(23.54).

Finally, in order to compare our results also

with time-dependent measurements we calculate

(!, T). Regarding the frequency dependence of n

we mention the following: A dynamical generaliza-

tion of the BKT theory has been developed by Am-

begaokar et al. [90,95]. It turns out that the critical

size for a vortex–antivortex pair is given by



2!

, (23.67)

where D



denotes the corresponding diffusion con-

stant. Only pairs with size r ≤ r

contribute to the

screening. Unfortunately, D



is not easy to calculate.

In the absence of pinning,the theory by Bardeen and

Stephen yields [96]



2c







, (23.68)

where c is the speed of light, 

∼ r

/2corresponds

to the coherence length,

denotes the normal-state

resistivity, 

= hc/2e is the elementary supercon-

ducting ﬂux quantum, and

d corresponds to an ef-

fective layer thickness. However, in cuprate super-

conductors, pinning becomes important. Thus, we

assume a simple Arrhenius law



= D



exp



−E



, (23.69)

In FLEX theory the ﬂuctuations of the ordered antiferromagnetic state in the paramagnetic metallic regime are treated

beyond the mean-field level. However, the ﬂuctuations of the superconducting condensate were neglected in earlier

treatments.A detailed comparison between n

(!) within the XY model and the FLEX approximation is given in [92,94].

1446 D. Manske,I. Eremin, and K.H.Bennemann

where E

denotes the corresponding pinning energy

barrier. Equations (23.69) and (23.68) are inserted

into (23.67) yielding a new length scale l in (23.62)

and (23.63),namely a new upper limit l =ln(r

Thus, we get n

(!, T)/m

∗

= ! Im (!)/e

where

the conductivity  (!) is obtained from the current–

current correlation function. Since 1/! ∼ time,and

we refer to the time of an observation, we expect

phase coherence already for !  1, where  refers

to the lifetime of phase ﬂuctuations.

Resum´e

In summary, we have demonstrated on general

grounds that the interplay between Cooper-pair con-

densation energy and phase ﬂuctuation energy al-

ready yields an optimal doping concentration. Thus,

the phase diagram can be described in the overdoped

part by T

∝ 

and in the underdoped case by T

∝

. The superconducting transition temperature T

in underdoped cuprates might be estimated by the

BKT theory.It is interestingthat n

=(m/e

)!



(!)

gives n

∝ 

if (!



/

)

!=0

=const.Such

a scaling was noted by C. Homes et al. [97]. For un-

derdoped cuprates one observes (

)

T→T

to be

independent of T.

The dynamical stiffness ∝ n

(!)providesinfor-

mation about the time-scale of Cooper-pair phase

ﬂuctuations. In our theory these are treated classi-

cally and the coupling between amplitude and phase

has been neglected.The results for n

(!)canbecom-

pared with time-resolved measurements. Note that

for ! > !

phase

,where!

phase

refer to the phase ﬂuc-

tuations, one expects a behavior as in the absence

of the phase ﬂuctuations. Thus n

(!) → n

(T, x)in

the absence of the Copper-pair phase ﬂuctuations.

We further would like to mention that phase ﬂuctu-

ations are also related to the formation of vortices.

For details see Appendix D.

23.2.8 Tunneling Spectra

A most important verification of the approxi-

mate validity of the conventional Eliashberg the-

ory came from electron tunneling experiments.

They probe the k-averaged quasiparticle excita-

tion spectra in the normal and superconducting

state. Therefore, in the case of singlet pairing in

high-T

cuprates and triplet pairing in ruthenates

also important fingerprints of the spin-ﬂuctuation-

mediated pairing interaction can be seen. Hence, we

nowanalyze tunneling in superconductor–insulator–

normal metal (SIN) and superconductor–insulator–

superconductor (SIS) junctions.

Using standard tunneling theory [98] we have

H = H

+ H

, (23.70)

where H

) is the Hamiltonian for particles on the

left-hand side (right-hand side) of the tunnel junc-

tion. Note, H contains all many-body effects. Here,

in general, [H

, H

]=0.H

denotes the tunnel op-

erator with a matrix element T

. The total current

through the tunnel junction can be expressed as the

average rate of change per time t of the number of

particles. For example, on the left-hand-side of the

junction ( =1),

tot

(t)=−e 

(t) (23.71)

=−ei



−∞



[N

(t), H



)] .

Aftersomealgebra[73]onearrivesat

tot

(t)=I

(t)+I

(t) ,

where

(t)=e

∞



−∞



(t − t



) (23.72)



ieV(t



−t)

[A(t), A



)] 

−e

ieV(t−t



)

[A

(t), A(t



)] 



and

(t)=e

∞



−∞



(t − t



) (23.73)



−ieV(t



+t)

[A(t), A(t



)] 

−e

ieV(t+t



)

[A

(t), A



)] 



Here, I

refers to the single-particle tunneling and

describes tunneling of Cooper-pairs, the Joseph-

son effect. The operator A is given by A(t)=

23 Electronic Theory for Superconductivity 1447



k,p

(t)c

(t)wherec

) refers to the single-

particle creation(annihilation)operator entering the

Hubbard Hamiltonian, and eV is the applied voltage.

In order to study the single-particle excitations

we focus in the following on I

. A closer inspection

of (23.73) shows that the current can be expressed as

I ∝ (G

red

− G

adv

)whereG

red

adv

) is the retarded

(advanced) Green’s function that correspond to the

operator A. This would lead to I

=−2e Im (G

red

)

and is important for SIS junctions. In the case of SIN

tunneling one obtains [73,76]

=2e



k,p

∞



−∞

2

(k, !) (23.74)

× A

(p, ! +eV)



f (!)−f (! +eV)



where f (!) again denotes the Fermi distribution

function and A

and A

is the spectral density of

the left-hand-side (sc-state) and right-hand-side (n-

state) material, respectively. The factor 2 arises from

the spin summation.The matrix element T

k,p

(i.e.the

transfer rate) varies on the energy scale E/E

which

should be negligible if E  

. Thus, an adequate

approximation should be to take T

k,p

= T

=const.

Note the elementary excitations are entering in

(23.75) via A(k, !). In particular, the frequency de-

pendence of the gap, (!), reﬂecting the dynamics

of the Cooper-pairing is of importance. Performing

the sum over momenta we obtain the important re-

sult that the single-particle density of states N(!)is

proportional to the dynamical conductivity dI

/dV

(normalized by its normal-state value) for a SIN tun-

neling junction system measured at ! =eVwithV

being the applied voltage:



tun

(eV) =

(eV)

∝



A(k, !)=N(!) . (23.75)

Obviously,below T

the tunneling density of states



tun

(eV) in cuprates reveals interesting structures

due to the interaction of quasiparticles with antifer-

romagnetic spin ﬂuctuations and the opening of the

superconducting gap.What is the energy position of

these structures? In the superconducting state the

spin ﬂuctuation spectrum is peaked at the resonance

energy !

res

. Thus, the structure in the NIS tunneling

occurs at

res

+ 

(NIS) . (23.76)

This follows immediately from (23.75), since the

spectral density A(k, !) in the superconductor re-

ﬂects !

res

and the shift of the quasiparticle density

by 

In the case of SIS tunneling the characteristic fea-

tureinthe tunnelingspectrumis shiftedto the higher

energy

res

+2

(SIS) . (23.77)

Again, in addition to !

res

each spectral density shifts

the energy by 

The maximum gap value 

and the resonance

frequency !

res

are both doping dependent quanti-

ties. As mentioned earlier to a good approximation

one finds !

res

(x) ∝ 2

(x)andT

 T

∗

∝ 

in the

overdoped case and !

res

(x) ∝ !

(x)intheunder-

dopedcuprates.Thus,in overdoped cupratesa reduc-

tion of spectral weight (“dip”) is expected at around

res

+

 3

(SIN),and in underdoped cupratesat

res

+ 

 !

+ 

(SIN).Similarly we get for over-

doped cuprates structure at !

res

+2

 4

(SIS),

and for underdoped ones at !

res

+2

 !

+2

(SIS). We will see later in Sect. 23.4.8 that this agrees

well with available experimental data [20,99]. There-

fore, we may safely conclude that as in the BCS and

conventional Eliashberg theory the single-particle

tunneling spectrum reﬂects the density of states and

thus provides insight into the strength and dynamics

of the Cooper-pairing.

Finally,we wouldlike to mentionthat for electron–

phonon mediated superconductivity the spectrum

of the pairing potential is mainly unchanged in the

superconducting state with respect to the normal

state. Thus, structure in the tunneling spectrum is

expected at an energy !

where !

is the Debye

frequency. In contrast to this, in the case of spin-

ﬂuctuation-mediated Cooper-pairing strong feed-

back effects are present yielding anisotropic elemen-

tary excitations and a renormalized spin spectrum

→ !

res

). This leads to the structure described

above and is clearly a direct fingerprint of Cooper-

pairing by spin ﬂuctuations and is expected for both

hole-dope and electron-doped cuprates. In addition,

1448 D. Manske,I. Eremin, and K.H.Bennemann

also the momentum dependence of the supercon-

ducting order parameter is reﬂected in the tunneling

spectrum. In particular, for an order parameter with

s-wave symmetry resulting from electron–phonon

interaction, one finds an isotropic density of states

with a gap for frequencies |!| < 2

.Incontrast,in

the case of unconventional superconductivity where

the order parameter has nodes, thermal excitations

with energies smaller than 2

arepossible(around

the nodes). Using thermodynamic arguments one

can easily show that the density of states has a linear

slope for ! → 0 [27]. Note that additional structure

might occur due to Andreev bound-states in SIN

and SIS tunneling, whichcannot be described by our

theory.

Note, the spectral density A(k, !) exhibits par-

ticle-hole asymmetry reﬂecting the correlations

amongst the quasiparticles. (see an early discussion

of this by Sawatzky et al.[100] and Bennemann et al.,

and others.)

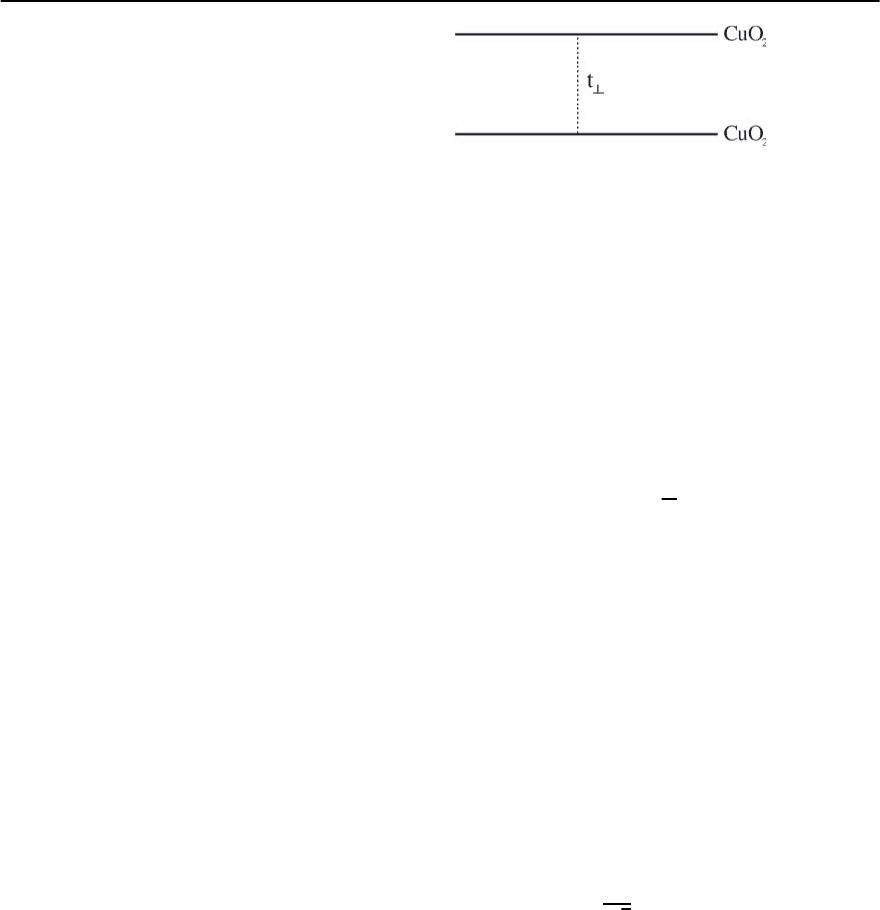
23.2.9 Bilayer Effects

Many high-T

cuprates contain more than one CuO

plane per unit cell like for example YBCO or BISSCO

compounds (see Fig. 23.2). So far,our theory has fo-

cused mainly on the physical properties of a single

CuO

-plane. Of course, it is desirable to understand

how the properties change if several CuO

-planes per

unit cell are present and how the number of CuO

layers per unit cell affects T

(x), for example. Note

that the bilayer coupling t

⊥

causes changes of the

Fermi surface topology and the dispersion 

.There

is also an interlayer coupling of Cooper-pairs. For

several CuO

-planes per unit cell also effects due

to varying hole doping are expected. The simplest

situation is illustrated in Fig. 23.24 where we show

schematically the coupling of two CuO

-planes via

the coupling parameter t

⊥

In the following we will present an extension of

the generalized Eliashberg-like theory for the case of

two coupled CuO

-planes [101,102]. We start from a

Hamiltonian that contains nearest and next nearest

neighbor hopping t and tt



, respectively, as well as

an intra-layer Coulomb repulsion U, an inter-layer

interactionV and an inter-layer hopping t

⊥

.Thecor-

Fig. 23.24. Illustration of the interlayer coupling t

⊥

affect-

ing the energy dispersion 

, Fermi surface and Cooper-

pairing across CuO

-layers. The magnetic coupling be-

tween the planes, J

⊥

, is not displayed. It is one order of

magnitude smaller than the in-plane (Heisenberg-like) su-

perexchange J



and thus is not considered in our electronic

theory.However,I

⊥

will split the spin-susceptibility into an

even and odd part, see neutron scattering experiments

responding Hamiltonian is given by

H = H

int

+ H

hop

, (23.78)

and with U

eff

= U

int

= U



il↑

il↓



i=j



il

jl



, (23.79)

and

hop

=−



i,jl

†

il

jl

− t

⊥



i

†

i1

i2

. (23.80)

Here, c

†

il

) creates (annihilates) an electron on

site i in the layer l =1orl =2withspin and

il

= c

†

il

. We diagonalize the Hamiltonian with

respect to the hopping term. Thus, we perform a

transformation in term of the operators d

k

with

the help of

kl





l

k

l

√



−ik

−e

−ik



, (23.81)

where  =+and = − denotes the bonding and

antibonding band,respectively, 2c is the distance be-

tween adjacent planes, and k is the in-plane momen-

tum. Thus, (23.80) can be rewritten as

hop



k

k1

, d

k2

)





(k)0

0 

−

(k)



k1

k2



(23.82)

23 Electronic Theory for Superconductivity 1449

with



=−2t



cos(k

)+cos(k

)

−2t



cos(k

)cos(k





∓ t

⊥

. (23.83)

One is now able to extend the generalized Eliash-

berg equations as described at the beginning of this

chapter. The corresponding Bethe–Salpeter equa-

tions separate with respect to band indices into two

sets of coupled equations [101,103]. If, forsimplicity

the inter-plane Coulomb repulsion V is neglected we

find six coupled equations for the self-energy com-

ponents:

i

(k, !)=N

−1







=+,−

∞



d§





(k − k



, §)

+(ı

 0

+ ı

 3

− ı

 1

) P



(k − k



, §)



∞



−∞



I(!, §, !



i



, !



) , (23.84)

(for a comparison, see (23.23)). In a shorthand nota-

tion we get



(k)=





(k − k



) G



) , (23.85)

where V



is the effective pairing interaction due to

spin (and also charge) ﬂuctuations.

Obviously, V and thus the dynamical spin suscep-

tibilities 

s,c

are 2 × 2 matrices in the layer indices,

having elements diagonal (

,

) and off-diagonal

(

, 

) with respect to the layer indices. The com-

ponents of the spin susceptibility transforming as

even and odd with respect to the layer indices are

given by 

= 

+

and 

= 

+

.Foriden-

tical planes 

= 

and 

= 

.Themeasured

susceptibility is then given

(q, q

, !)=

(q, !)cos





+ 

(q, !)sin





, (23.86)

where c is the separation of the layers within a unit

cell,q isthein-planewavevector,andq

denotes the

component perpendicular to the planes. Note, if in

cuprates or ruthenates the spin response in INS ex-

periments would dominate at the wave vector q

= ,

for example, one would expect that 

 

(23.86).

23.2.10 Electron-Doped Cuprates

Although we discussed in the previous chapters al-

ready the differences and similarities of electron-

doped and hole-doped cuprates (in particular the

evolution of antiferromagnetism as a function of the

doping concentration) it is of interest to summarize

the significantproperties of the electron-doped com-

pounds. The understanding of the phase diagram of

the electron-doped cuprates should play a role in re-

solving the physics of cuprates in general.

In Fig. 23.25 we show the phase diagram for the

metallic phase of electron-doped cuprates. The be-

havior of T

upon doping follows a parabolic-like

curve with a narrow doping range for which super-

conductivity occurs.Therefore,despite the rather dif-

ferentbehavior ofthe spin ﬂuctuationsinhole-doped

(localized) and electron-doped (itinerant) cuprates

the doping dependence of the T

curve looks simi-

lar in hole-doped and electron-doped cuprates. This

suggests the same mechanism for Cooper-pairing

and, most importantly, indicates the similar role

played by the localized and itinerant spin ﬂuctua-

tions. The appearance of the“pseudogap”in the elec-

tronic spectrum of electron-doped cuprates has been

debated for a long time.Recently its existence in the

presence of a high magnetic field has been confirmed

by careful tunneling spectroscopy by Alff et al. [77].

In particular, it has been found that the pseudogap

shows a very similar doping dependence as in hole-

doped cuprates, but its temperature range is lower.

Moreover, as seen from Fig. 23.25 as in hole-cuprates

the energy scale of the pseudogap and superconduc-

tivity crosses each other around the optimal doping

and the pseudogap disappears in slightly overdoped

cuprates. This confirms the close similarity between

electron-doped and hole-doped cuprates regarding

most of the properties.It also suggests that the mech-

anism of superconductivity,symmetry of the super-

conducting order parameter,andtheanomalousnor-

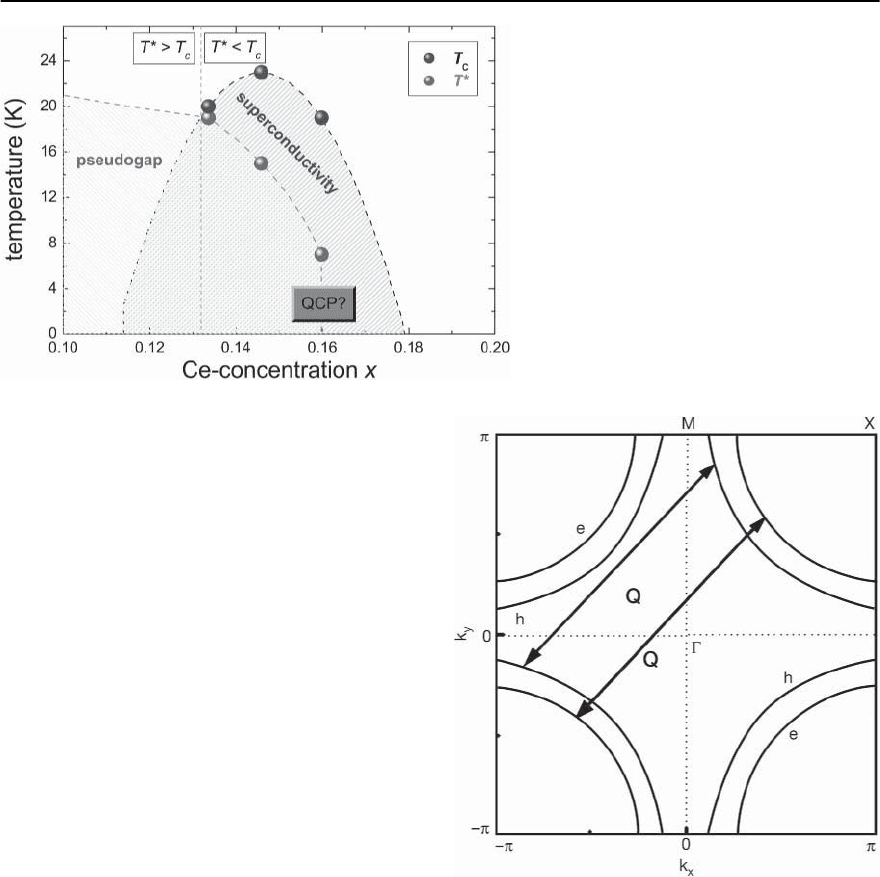
1450 D. Manske,I. Eremin, and K.H.Bennemann

Fig. 23.25. Phase diagram of the electron-doped

cuprates measured by tunneling experiments

on thin films (taken from [77]). Note the nar-

row range of superconductivity in electron-

doped cuprates,and the smaller energy scale of

the pseudogap. Both hole-doped and electron-

doped cuprates show a similar phase diagram

indicating the same mechanism for supercon-

ductivity below T

and pseudogap below for-

mation T

∗

.The doping concentration where the

pseudogap disappears may be related to a quan-

tum critical point (QCP)

mal state properties should have the same origin in

both compounds.

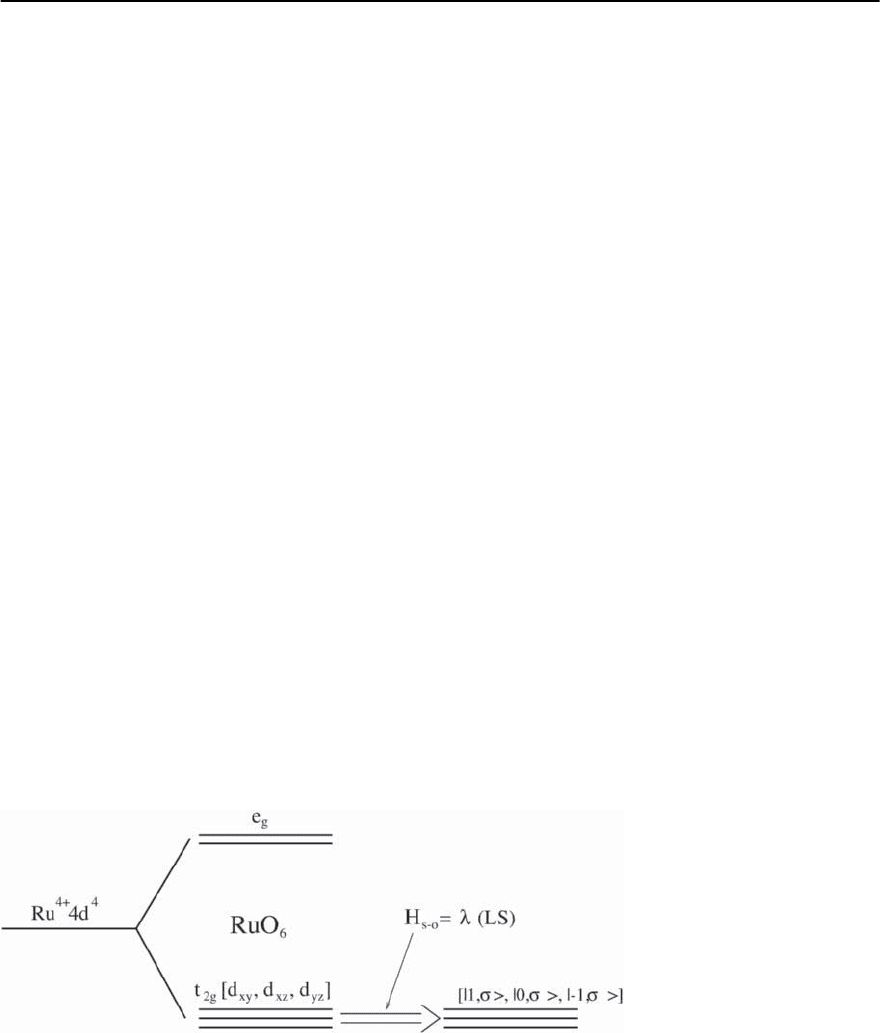
Inorder todiscussthemaindifferenceinFig.23.26

we show our results for the Fermi surface of the hole-

doped and electron-doped cuprates.These agree well

with available experimental data [104]. Remarkably,

the differences of the Fermi surfaces in the first BZ

in hole and electron-doped cuprates have important

consequences for their superconducting and normal

state properties. In particular, the antiferromagnetic

spin ﬂuctuations which are peaked at Q =(, )

connect different portions of the Fermi surface in

hole-doped and electron-doped cuprates as one can

see in Fig. 23.26. Inthe hole-doped cuprates the anti-

ferromagnetic wave vector connects the carriers that

lie close to the M =(, 0) point of the first BZ. This

means that the main scattering by the spin ﬂuctu-

ations occurs in hole-doped cuprates around these

points (so-called “hot spots”). On the other hand, in

the electron-doped cuprates the antiferromagnetic

wave vector Q =(, ) connects carriers that are

close to the diagonal of the BZ. Therefore, the main

effect of the interaction will occur there. This will be

reﬂected in the asymmetrical behavior of the hole-

doped and electron-doped cuprates.

What are the consequences for the superconduct-

ing state? In particular, we expect the appearance

of the higher harmonics in the d

−y

-wave super-

conducting order parameter in the electron-doped

Fig. 23.26. Tight-binding results for the Fermi surface for

hole-doped (h) and electron-doped (e) cuprates at optimal

doping.  =(0, 0), M =( , 0), and X =( ,  )denotethe

symmetry points of the first Brillouin zone. Remarkably

the topologyof the Fermi surface is hole-like in bothcases.

Q =( ,  ) refers to the antiferromagnetic wave vector

cuprates, since the Cooper-pairing occurs far from

the antinodal M points and close to the diagonals

of the Brillouin zone. Furthermore, due to a weaker

(weaker than in hole-doped cuprates) nesting of the

23 Electronic Theory for Superconductivity 1451

Fermi surface the non-Fermi-liquid behavior and

antiferromagnetic ﬂuctuations should also be less

pronounced in the electron-doped cuprates. Lattice

vibrations may play a role for superconductivity in

the overdoped part of the electron-doped phase di-

agram. For T

→ 0 a competition between quasi-

particles coupling to spin ﬂuctuations and phonons

may for energetic reasons in principle cause a change

from d

−y

-symmetry to s-symmetry of the super-

conducting order parameter. Such a scenario could

be formulated using Ginzburg–Landau theory.

To summarize, we show that the differences be-

tween hole-doped and electron-doped cuprates are

expected due to differences in their Fermi surfaces

and density of states. As a result of this, the scatter-

ing by spin ﬂuctuations plays a more important role

around M =(, 0) points of the BZ in hole-doped

cuprates.On the contrary, the scattering by spin ﬂuc-

tuations occurs close to the diagonals of the BZ in

the electron-doped cuprates.This will be reﬂected in

the asymmetric behavior between hole-doped and

electron-doped cuprates in the normal and super-

conducting states.

23.3 Electronic Theory for Ruthenates

(Sr

RuO

)

We d iscu ss Sr

RuO

in detail, since triplet Cooper-

pairing seems present as maybe also realized in some

heavy fermion systems.What may cause triplet pair-

ing,since both ferromagnetic and antiferromagnetic

spin ﬂuctuations are present in the ruthenates? What

is the effect of the strong magnetic anisotropy on su-

perconductivity and its thermodynamic properties?

23.3.1 Electronic Structure and the Hamiltonian

We present now the electronic theory for Sr

RuO

which exhibits a superconducting transition temper-

ature T

=1.5 K. Effects involving all bands crossing

the Fermi level are expected to play an important role

in determining the triplet superconductivity in this

compound. We will start the analysis by calculating

the electronic structure of Sr

RuO

. In Fig. 23.27 we

illustrate the basic electronic structure of Sr

RuO

The highly planar structure ofSr

RuO

prevents sub-

stantial energy dispersion along thez-direction.Note

the large interplanar separation of the RuO

octahe-

dra. At the same time in the ab-plane neighboring

RuO

-octahedra share O ions which in turn are -

bonded to the Ru ions. Thus,the xy-orbitalwill form

a two-dimensional band, while the xz and yz-bands

have only a restrictedone-dimensional character.For

the metallic properties one has to take into account

intermediate electronic correlations.

Then an effective Hamiltonian for describing the

physics in Sr

RuO

is a two-dimensional three-band

Hubbard Hamiltonian

H =



k,





k˛

k,˛



i,˛

i˛↑

i˛↓

(23.87)

Fig. 23.27. Electronic structure of Sr

RuO

including an effective spin-orbit coupling between d

, d

,andd

states. Due

to a mixing of spin and orbital degrees of freedom the new states are characterized by pseudo-spin and pseudo-orbital

quantum numbers.Since the spin-orbit coupling H

s−o

does not break the time-reversal symmetry the Kramers degeneracy

between the spin up and down is not removed