Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors
Подождите немного. Документ загружается.

1472 D. Manske,I. Eremin, and K.H.Bennemann
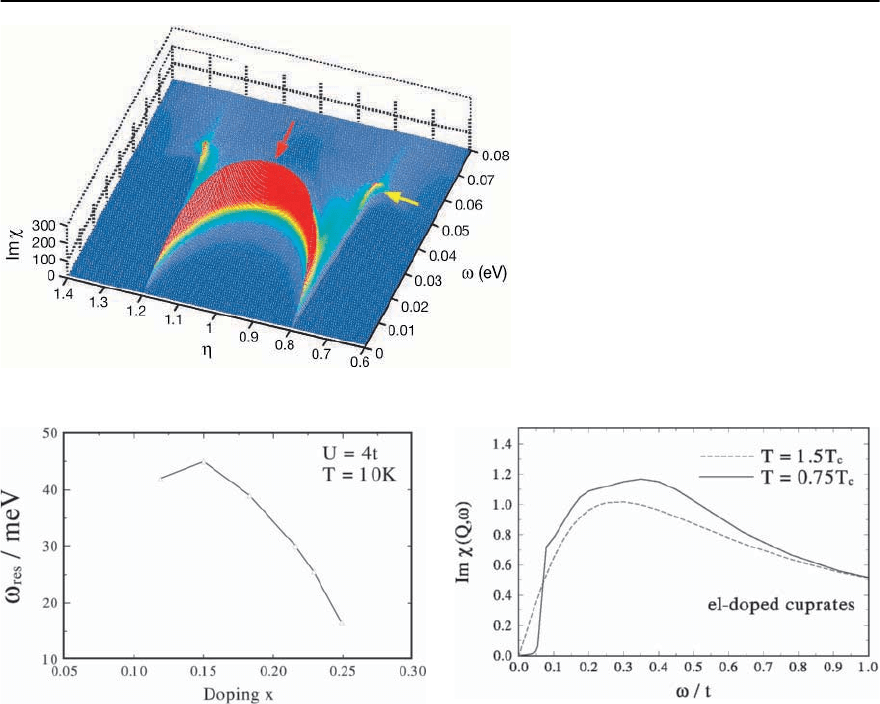
Fig. 23.45. RPA results for magnetic excitations
in a d
x
2
−y
2 superconductor.Im obtained from
Eq. (23.38) with U = g(q)asafunctionofmo-
mentum [along q=( , )] and frequency in
the SC state. We use
k
=
0
(cos k
x
−cosk
y
)/2
with
0
=42meV,andg(q) weakly peaked at
(, ): g(q)=q
0
[1 − 0.1(cosq
x
+cosq
y
)] with
q
0
=0.572 eV, in order to reproduce the correct
energy position of the Q
∗
mode near 0.8(,
and the Q mode at (, ))
Fig. 23.46. FLEX results for !
res
versus doping in monolay-
ered cuprates. In the overdoped regime with T
c
∝
0
we
find a constant ratio of !
res
/T
c
.Notethatt = 275 meV has
been used
thus the energy position of the resonance peak will
also decrease. In the underdoped cuprates the situa-
tion is different. In this case, the system is very close
to an antiferromagnetic instability and thus the ef-
fect of superconductivity on the formation of the res-
onance peak consists only of reducing the damping.
This helps to satisfy the resonant condition. The fre-
quency position of the resonance peak will be rather
set by the normal state frequency !
sf
. Since !
sf
gets
smaller with decreasing doping the resonance peak
position also decreases in the underdoped cuprates.
To summarize, we obtain for the position of the
resonance:
Fig. 23.47. The imaginary part of the spin susceptibility
for the electron–doped cuprates above and below T
c
at
q = Q =(, ) calculated using the FLEX theory. The
calculations are performed for U =4t and for an opti-
mal doping concentration x =0.15. No resonance peak
is found. Only a rearrangement of spectral weight due to
(!)occurs
!
res
≈
!
sf
, underdoped
2
0
, overdoped .
(23.133)
In the optimal doped case (which corresponds ap-
proximately to x =0.15 holes per copper site) the
resonance energy is slightly lower than 2
0
.Physi-
cally,this corresponds to a bound state inside the gap
region. Let us also comment on the spin dynamics
of the electron-doped cuprates. As we have already
mentioned the nesting properties in the electron-

23 Electronic Theory for Superconductivity 1473
doped cuprates are much weaker and fewer density
of states are available, and thus they are far from
the antiferromagnetic instability. As a result, calcu-
lating Im(Q, !)wefindthat!
sf
becomes larger
than in hole-doped cuprates and less pronounced as
shown in Fig. 23.47. This has an important conse-
quence also for the feedback of superconductivity. In
particular, we find that the resonance condition, i.e.
(23.43),in the electron-doped cuprates cannot be ful-
filled andthespin excitation spectrumisonly slightly
renormalized due to the superconducting gap. (Note
that one might argue that due to the singularity in
Re(Q, ! =2
0
), a resonance condition could al-
ways be fulfilled and thus a resonance peak must
occur for a d
x
2
−y
2
-wave gap.However,this singularity
is of logarithmic-type and thus less spectral weight is
available for an increasing U. Numerical calculation
showthatalready for U 4t there exits no resonance
peak at T =0.)
We would like to stress that despite the absence of
the resonance peak in electron-doped cuprates the
superconducting instabilityis nevertheless driven by
the spin fluctuations.
To summarize, we have shown that the spin dy-
namicsincupratesaboveandbelowT
c
can be suc-
cessfully explained on the basis of the one-band Hub-
bard Hamiltonian and RPA spin susceptibility em-
ploying the FLEX approximation.Important features
like resonance peak and magnetic coherence occur
in the superconducting state of hole-doped cuprates
due to the feedback of superconductivity and rear-
rangement of the normal state spin excitation spec-
trum calculated within the self-consistent Eliashberg
approach for various doping concentrations. Our re-
sults are also qualitatively similar to the those of the
spin-fermion model [58]. Improved calculations of
(q, !) should include the local character of the Cu-
spins.
23.4.6 Phase Diagram for Electron-Doped and
Hole-Doped Cuprates
We demonstrate that our electronic theory assum-
ing the exchange of antiferromagnetic spin fluctu-
ations as a relevant pairing mechanism for singlet
pairing in cuprates can account for the main fea-
tures in the phase diagram of hole-doped cuprates.
In particular, we determine the doping dependence
of the characteristic temperatures of the phase dia-
gram,namely T
∗
c
(x),T
c
(x),and also T
∗
at which a gap
appears in the spectral density. Below T
∗
c
we indeed
find incoherent Cooper-pairs (“pre-formed pairs”),
which become phase coherent only below the criti-
cal temperature T
c
. We will show that phase fluctu-
ations contributing F
phase
to the free energy lead
to a decreasing critical temperature in the under-
doped regime, T
∗
c
→ T
c
, and thus to the appearance
of an optimal doping x
opt
. It is shown that this result
is due to the small superfluid density n
s
(T)inthe
system. Most importantly, for x > x
opt
we find that
Cooper-pair phase fluctuations cost too much energy
(F
phase
∝ n
s
)andthusT
c
∝
0
,whileforx < x
opt
one gets T
c
∝ F
phase
.NotethatatT
c
the Meissner
effect occurs. F
cond
denotes the contribution to the
free energy due to Cooper-pair formation and F
phase
refers to the contribution due to phase fluctuations of
the Cooper-pairs.We compare our results with those
of Berezinskii–Kosterlitz–Thouless (BKT) theory as
well as with the XY model.
In Fig. 23.48 we show our results for the phase
diagram of hole-doped cuprates together with the
experimental curve. T
∗
c
was obtained from the lin-
earized Eliashberg equations.In optimally and over-
doped cuprates one clearly sees that the results of
FLEX calculations and experiments agree well with
each other, T
∗
c
≈ T
c
and T
c
∝
0
(x). Due to a weak-
ening of the nesting properties of the Fermi sur-
face upon increasing doping and corresponding sup-
pression of antiferromagnetic spin fluctuations the
superconducting transition temperature goes down
and we do not find any superconductivity above
x =0.3.On theotherhand,in theunderdoped regime
the T
c
curve in the FLEX approach still slightly in-
creases while in experiments it decreases and super-
conductivity does not exist below x =0.05.
The slight increase of T
c
upon lowering the dop-
ing below optimal one is the result of the shape of
the Fermi surface and of the large scattering rate
that prevent more and more Cooper-pairing. In our
model the Fermi surface becomes closer to nesting
and thus the corresponding spin fluctuations respon-
sible for superconductivity get enhanced. This indi-
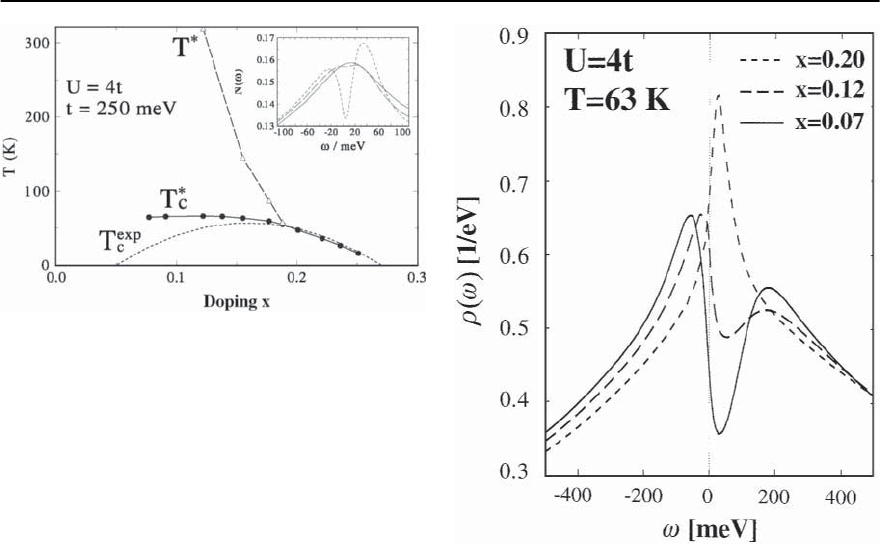
1474 D. Manske,I. Eremin, and K.H.Bennemann
Fig. 23.48. Results for the phase diagram of hole-doped
cuprates using the one-band Hubbard model. Cooper-pair
phase fluctuations are neglected. Note,x =1−n and on-
site Coulomb repulsion is U =4t,wheret is the nearest
neighbor hopping integral. Below the pseudogap temper-
ature T
∗
(dashed line) one finds a reduction of spectral
weight in the density of states at ! = 0 (see in set). T
∗
c
(solid line) denotes the superconducting transition tem-
perature neglecting Cooper-pair phase fluctuations. The
dashed-dotted line corresponds to a phenomenological fit
to experimental data T
exp
C
[132]. Inset: Density of states
N(!)inunits1/t for doping x =0.15 at temperature
T =4.5T
∗
c
(solid line), T =2.3T
∗
c
≡ T
∗
(dashed line),
and T =1.01T
∗
c
(dotted line)
cates that the model we have used in the mean-field
is not applicable for the underdoped cuprates. In the
vicinity ofantiferromagnetismthe effectsoftheelec-
tronic correlations play an important role. The per-
turbativeapproachweareusingwillnotproperly
account of the correlations. For example, it is known
from ARPES experiments [134] that the shape of the
Fermi surface changes in hole underdoped cuprates
and forms pockets around (/2, /2) points of BZ,
which is believed to be a result of the electronic cor-
relations. Also, note that a pseudogap opens up in
the elementary excitation spectrum, see Fig. 23.49.
Furthermore, Cooper-pair phase fluctuations matter
and suppress T
c
. We will present results for this case
later, see Fig. 23.51.
In the Eliashberg formulation of the Cooper-
pairing the carriers not only pair, but also scatter
due to spin fluctuations. If the scattering is strong
some of the quasiparticles will be away from the
Fermi level already in the normal state. This forms
Fig. 23.49. Calculated doping dependence of the pseudogap
that occurs below T
∗
in the electronic density of states in
the normal state of hole-doped cuprates for a fixed temper-
ature T = 63 K. For small doping this pseudogap appears
dueto the scattering of quasiparticles byantiferromagnetic
spin fluctuations. With decreasing doping the pseudogap
increases. This agrees well with experimental data [133].
Moreover, for underdoped cuprates the value of the calcu-
lated pseudogap (taken as a distance between the edges)
p
≈ 80 meV is similar to that measured in underdoped
cuprates
exp
p
≈ 88 meV [133]
a dip, i.e. the reduction of the spectral weight in the
density of states at the Fermi level as one can see
from the inset of Fig. 23.48. In order to investigate
the doping dependence of such a pseudogap in the
density of states more in detail,in Fig.23.49 we show
the calculated results for N(!) for various doping.
One clearly sees that in the overdoped region the
density of states is unrenormalized due to weakness
of the antiferromagnetic correlation.For decreasing
doping a pseudogap at the Fermi level occurs and
it increases upon decreasing doping. The pseudogap
opens below T = T
∗
. Results for T
∗
using U =4t
as a function of hole-doping are shown in Fig. 23.48.
23 Electronic Theory for Superconductivity 1475
Table 23.1. Results for the calculated pseudogap forma-
tion temperature T
∗
resulting from the scattering of car-
riers by spin fluctuations for different doping in compar-
ison with experimental data on T
∗
exp
found in YBaCuO-
compounds [135]
xT
∗
(K) T
∗
exp
(K)
0.16 100 90
0.15 150 160
0.14 200 190
0.13 310 240
Most importantly,our results show a good agreement
for the doping dependence of the pseudogap. Simi-
lar to the NIS tunneling experimental data [133] the
pseudogap increases with decreasing doping from
overdoped to underdoped cuprates. In Table 23.1 we
show our calculated results for T
∗
using U =4t for
different doping in comparison with experimental
data onYBaCuO-compounds [135]. One notices that
our results agree also well on the quantitative level.
Moreover, for the underdoped cuprates the calcu-
lated magnitude of the pseudogap taken as a dis-
tance between edges of two peaks (
p
≈ 80 meV
at x =0.07) agrees well with the experimental value
exp
p
= 88 meV foundfor underdoped cuprates [133].
For completeness it remains to be seen whether the
same theory can explain also the phase diagram of
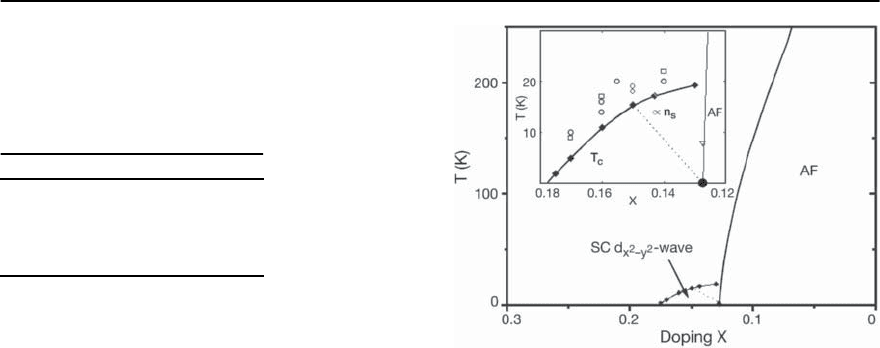
electron-doped cuprates. In Fig. 23.50 we present
the results of FLEX calculations for electron-doped
cuprates [122]. Most importantly our mean-field re-
sults for the phase diagram are in good agreement
with experimental data again for optimally and over-
doped region. For example, one sees that the maxi-
mal T
c
is smaller than in the hole-doped case. The
reasons for this are poorer nesting properties of the
Fermi surface in electron-doped case and also the
fact that a flat bands lies in NCCO is approximately
300 meV below the Fermi level. Another important
feature of the phase diagram of the electron-doped
cuprates is the narrower range of superconductivity
than in the hole-doped case (0.12 < x < 0.18 in the
electron-doped case and 0.05 < x < 0.3 for hole-
doped cuprates). The reason for this is also clear:
in the overdoped regime the nesting properties of
electron-doped NCCO rapidly become very poor and
cannot drive superconductivity. In the underdoped
Fig. 23.50. Results for the phase diagram of electron-doped
cuprates using the one-band Hubbard model. We neglect
Cooper-pair phase and amplitude fluctuations, thus T
∗
c
=
T
c
. The hole doping concentration is x =1−n and the
on-site Coulomb repulsion U =4t,wheret is the nearest
neighbor hopping integral. The inset shows the region of
superconductivity.The antiferromagnetic (AF) transition
curve is taken from [136]. The solid curve corresponds to
our calculated T
c
values [122]. The experimental data are
squares from [137],triangles from [138],circles from [139].
The dashed curve corresponds to T
c
∝ n
s
as in hole-doped
cuprates
regime one should keep in mind that antiferromag-
netism persists in the electron-doped case for larger
doping. Thus, the superconductivity region will be
further destroyed by the antiferromagnetic instabil-
ity that competes with the superconducting one.
Similarly to hole-doped cuprates the important
question is how T
c
is lowered in the underdoped
regime. Our calculations have shown in agreement
with experiment that there is no weak pseudogap
above T
c
in the underdoped regime of the electron-
doped cuprates in contrast to the hole-doped ones.
The reason is clear: The spin fluctuations are less
pronounced in the electron-doped cuprates and thus
do not produce a dip in the spectral density at the
Fermi level.
We now present results for T
c
(x)intheunder-
doped cuprates (x < x
opt
) including Cooper-pair
phase fluctuations. The region x < x
opt
can be ex-
perimentally characterized by a T
c
that decreases
with decreasing hole density x.Furthermore,theso-
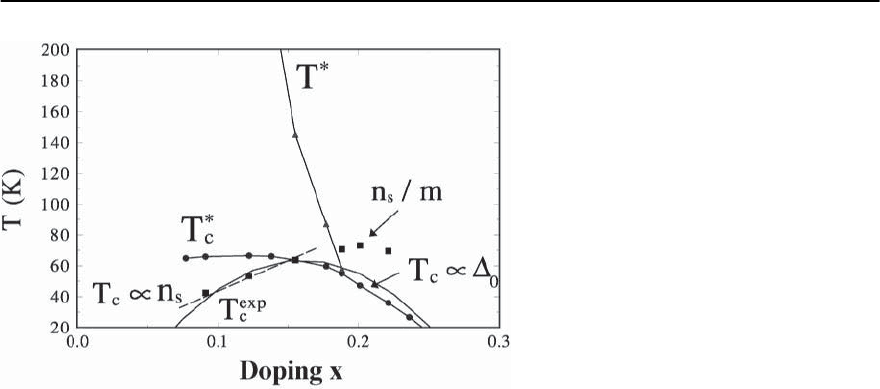
1476 D. Manske,I. Eremin, and K.H.Bennemann
Fig. 23.51. Phase diagram for high-T
c
super-
conductors resulting from a spin fluctuation
induced Cooper-pairing including their phase
fluctuations. The calculated values for n
s
(0)/m
(squares) are in good agreement with muon-
spin rotation experiments [141]. They deter-
mine the energy costs for the Cooper-pair
phase fluctuations. T
∗
c
denotes the tempera-
ture below which Cooper-pairs are formed.The
dashed curve refers to our calculated results
using n
s
(x)andgivestheobservedUemura
scaling T
c
∝ n
s
(T =0, x) [14]. As shown
in Figs. 23.50 and 23.49 below T
∗
we get a
gap structure in the spectral density as ob-
served in tunneling spectroscopy [20,142].The
solid curve T
exp
c
refers to experiments describ-
ing many hole-doped superconductors [132]
called Uemura scaling holds [14]. It was recognized
early on that a small n
s
leads to a reduced stiffness
against fluctuations of the phase of the supercon-
ducting order parameter [78,79,140]. Furthermore,
cuprate superconductors consist of weakly-coupled
CuO
2
planes so that Cooper-pair phase fluctuations
are enhanced also by the reduced dimensionality.
Note that in conventional superconductorsthis is not
relevant, since the large superfluid density leads to a
typical energy scale of Cooper-pair phase fluctua-
tions much larger than the superconducting energy
gap that governs the thermal breaking of a Cooper-
pair. Thus, in conventional superconductors T
c
∝
(T =0)[76].Incontrasttothis,theobservation
T
c
∝ n
s
in underdoped (hole-doped) cuprates indi-
cates that Cooper-pair phase fluctuations drive the
superconducting instability. The Cooper-pairs only
break up at a crossover temperature T
∗
c
> T
c
and
between T
c
and T
∗
c
local phase-incoherent Cooper-
pairs exist [70,78,79,93,140].Thena transition to su-
perconductivity with phase-coherent Cooper-pairs
occurs at T
c
∝ n
s
[70,78,79].
Using results for n
s
(x, T)calculatedfromKubo
formula for the underdoped cuprates we obtain the
phase diagram shown in Fig. 23.51. In the overdoped
regime T
∗
c
is identical with the bulk transition tem-
perature T
c
below which a Meissner effect is found.In
agreement with experiments from our electronic the-
ory we get T
c
∝ (T → 0) for overdoped cuprates.
In the overdoped cuprates the energy costs due to
Cooper-pair phase fluctuations (∝ n
s
/m)arehigher
than the condensation energy. Then, Cooper-pair
phase fluctuations play a minor role in determining
T
c
in the overdoped cuprates. In contrast to this, in
the underdoped cuprates we find T
c
∝ n
s
(x) ∝ T
∗
c
.
This results from the low superfluid density n
s
.AtT
∗
c
phase-incoherent Cooper-pairs are formed and only
at T
c
< T
∗
c
does one get phase coherence (quantum
phase fluctuations at T
c
= 0 have not been included).
Our theory shows that for optimal doping oc-
curs as a result of replacing, determining T
c
,the
free energy change F
cond
(x)duetoCooper-pair
condensation for overdoped cuprates by the free
energy change F
phase
gained from phase coher-
ence of the Cooper-pairs. Thus, T
opt
c
occurs when
F
cond
= F
phase
∼ n
s
.
Resultsfor F(x) areshown in n Fig.23.52.We find
that F
cond
mainly follows the doping dependence of
the mean-field transition temperature T
∗
c
. The dop-
ing dependence of F
phase
(x)isgivenbyn
s
(0)/m.
Note that the energy cost due to phase fluctuations
has the opposite behavior to the energy gain due to
Cooper-pair condensation with respect to the dop-
ing concentration x.Itisremarkablethatfromour
electronic theory we get a crossing of the two en-
ergy contributionsF
cond
and F
phase
at x 0.15 for
which the largest T
c
is observed. The consequence
of this is that we find a non-monotonic doping de-
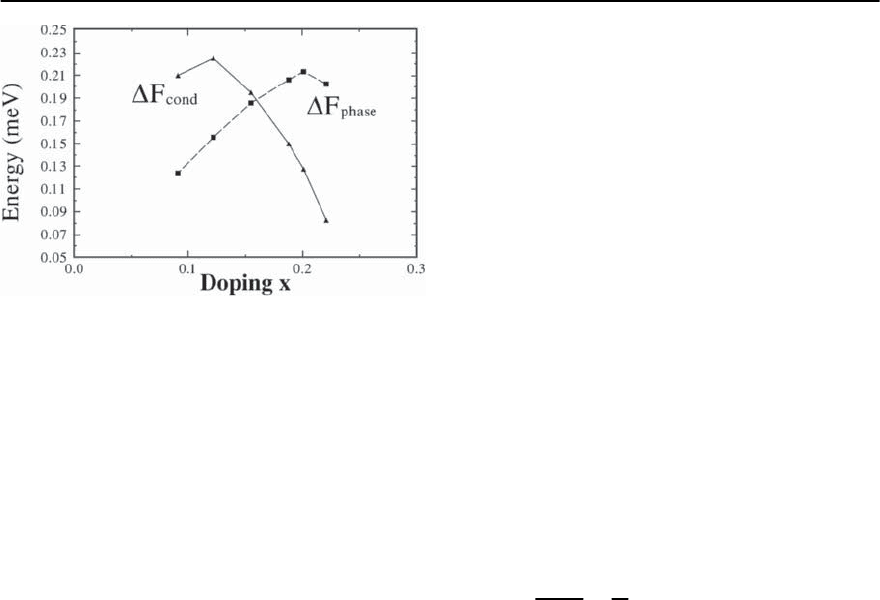
23 Electronic Theory for Superconductivity 1477
Fig. 23.52. Calculated crossover of the phase-stiffness en-
ergy and F
cond
. F
phase
∝ n
s
/m and the condensation
energy is F
cond
˛{n
s
/m}
0
(x). Here, we estimate ˛
2.5 ×10
−3
.(For comparison in conventional superconduc-
tor Al ˛ ≈ 0.4 [143]. Note that in cuprates ˛ is small
for two reasons, namely, the number of holes condensed
into Cooper-pairs is maximum 50% of the whole number
of carriers available and, secondly, due to the large size
of the unit cell of cuprates). Our results for ˛ agree well
with other theoretical and experimental estimates [83–85].
F
phase
< F
cond
implies the two characteristic tempera-
tures T
∗
c
, where Cooper-pairs are formed at T
c
∼
0
,and
T
c
≈ F
phase
∝ n
s
, where Cooper-pairs become phase co-
herent
pendence of T
c
(x) and optimal doping at x 0.15
and T
c
∝ n
s
for underdoped cuprates (and thus the
Uemura scaling).
Physically speaking in the overdoped regime we
find a large F
phase
, which means that Cooper-pair
phase fluctuations cost much energy. Thus, the sys-
tem will undergo a mean-field transition involving
phase coherent Cooper-pairs and a small condensa-
tion energy F
cond
(F
cond
∼ T
c
∝
0
< F
phase
). In
the underdoped cuprate superconductorsthe energy
gain due to the formation of Cooper-pairs is such
that they are broken up to T
∗
c
and T
∗
c
> T
c
.Onlyat
T ≤ T
c
does the phase coherence of theCooper-pairs
occur.
Note that the coherence length in electron-doped
cuprates estimated from H
c2
measurements is
ab
30Å [77], much larger than a typical value for the
hole-doped ones. This means that all Cooper-pairs
overlap well with each other and that almost all elec-
trons are involved in superconductivity. Therefore,
one expects that the Cooper-pair phase fluctuations
play amuchless importantrole in the electron-doped
cuprates than in hole-doped ones.
To summarize, we have solved the generalized
Eliashberg equations self-consistently and extended
them by including Cooper-pair phase fluctuations
to calculate some basic properties of the hole-doped
cuprate superconductors. The doping dependence of
T
c
(x) and an improved phase diagram is obtained.In
particular we show also results for the condensation
energy and for the weak pseudogap temperature T
∗
below which a small reductionin the spectral density
at the Fermi level appears.
23.4.7 Doping Dependence of the Superfluid Density
n
s
(x; T )
In Fig. 23.53 results for the temperature dependence
of the superfluid density n
s
(! =0)/n (n denotes
the normal-state band filling) are given below T
∗
c
for
various doping concentrations.We calculate n
s
using
the current–current correlation function and stan-
dard many-body theory [73], see Eq. (23.54):
n
s
(!)
m
=
1
e
2
! Im (!) . (23.134)
Note that according to London’s theory,
L
∝ n
s
,
the ratio n
s
/n is related to measurements of the
(in-plane) penetration depth; for an example see
microwave experiments. Note that our calculations
showthatroughlyonly1/3 of the holes become su-
perconducting, even for T → 0. This is typical for
a strongly interacting system. For decreasing doping
(x → 0) the curves n
s
(T) get flatter and smaller, as
experimentally observed.
For underdoped cuprates Cooper-pair phase fluc-
tuations become important (T
∗
c
< T
c
). Then, after
averaging over the phases of the Cooper-pairs one
expects of course n
s
→ 0 for T→ T
c
.Weillustrate
this in Fig.23.53 where we show experimental results
and FLEX results for underdoped cuprates. Then, a
qualitative agreement with the data of Bonn, Hardy
and co-workers on
2
(T =0)/
2
(T) concerning the
slope of the curves in the vicinityof T
∗
c
and the linear
behavior for T → 0 is found [8].
In particular the FLEX approximation for the gen-
eralized Eliashberg equations yields close to T
∗
c
a
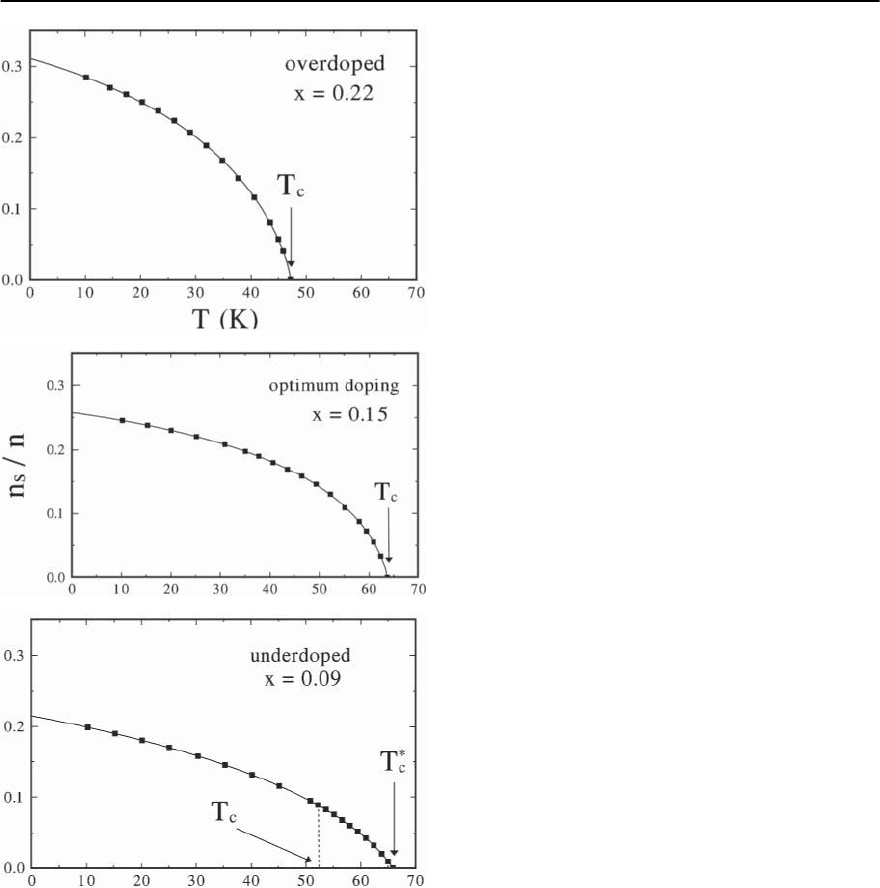
1478 D. Manske,I. Eremin, and K.H.Bennemann
Fig. 23.53. Temperature dependence of the superfluid den-
sity n
s
(x, T) calculated with the help of (23.51)–(23.54)
for various hole doping concentrations x.We extrapo-
late the results to T → 0. At temperature T such that
T
c
< T < T
∗
c
Cooper-pairs become phase incoherent,
n
0
s
→ 0. Our results are in fair agreement with measure-
ments of the in-plane penetration depth by Bonn, Hardy
and co-workers [8]. The dashed curve for the underdoped
case illustrates the effect of Cooper-pair phase fluctuations
according to the (static) Kosterlitz–Thouless theory
relation
3
(T =0)/
3
(T) ∝ (T
∗
c
− T). The same
power law was found by Kamal et al. and has been
attributedto criticalfluctuationsstarting about 10 K
below T
c
, since the slope coincides with the criti-
cal exponent for the 3D-XY model [8]. Here, we ob-
tain this power law from the generalized Eliashberg
equations using the FLEX approximation, which is
purely 2D and does not contain critical fluctuations.
Instead, the rapid increase of n
s
below T
∗
c
is due to
the self-consistent treatment of the superconducting
gap function (!). Thus, we conclude that while 3D
critical fluctuations are expected in a very narrow
temperature range close to T
c
,thesearenottheori-
gin of the observed power law on the scale of 10 K.
In Fig. 23.54 we present the FLEX results for
Cooper-pairing phase averaged superfluid density
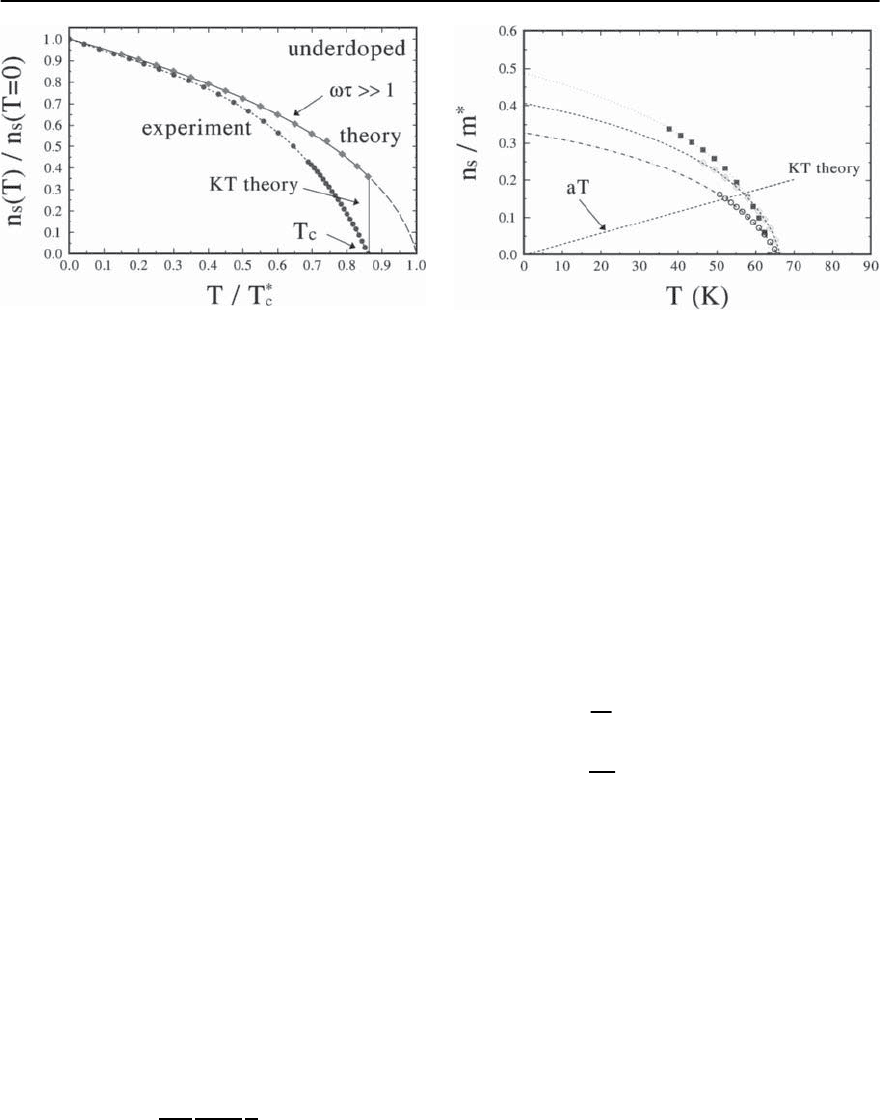
23 Electronic Theory for Superconductivity 1479
Fig. 23.54. Phase averaged superfluid density for under-
doped cuprates. The deviation of experimental results (cir-
cles) from FLEX results is due to Cooper-pair phase fluc-
tuations with lifetime . Taking these into account within
BKT theory one gets results indicated by the vertical line.
For the dynamical superfluid density (t ∼ !
−1
)oneex-
pects n
s
(t) → n
s
(FLEX) if ! 1
in underdoped superconductors. The effect of phase
fluctuations can be seen from the discrepancy be-
tween experiment [8] and theory. One clearly sees
that no Meissner effect results for T > T
c
, since
the phase correlation function < ∇(r) ·∇(0) >
becomes zero. The results obtained using static
Kosterlitz–Thouless theory (straight line) and the
FLEX results (diamonds) for n
s
(x, T) are shown. The
FLEX results neglect phase fluctuations, which is ap-
propriate for ! →∞. Of course, in Kosterlitz–
Thouless theory we get n
s
→ 0atT
c
.Notethatinour
full FLEX calculations we have to use for the phase
averaged superfluid density n
s
= n
0
s
∇(r) ·∇(0)
and then also n
s
→ 0atT
c
. Note that for T < T
c
the discrepancy between experimental results and
our FLEX calculations indicates the importance of
Cooper-pair phase fluctuations below T
c
.
In Fig. 23.55 we show results for n
s
renormalized
due to phase (vortex) fluctuations (for details see
Appendix D and [92]). The Berezinski–Kosterlitz–
Thouless (BKT) theory describes the unbinding of
thermally created pancake vortex–antivortex pairs.
The relevant parameters are the dimensionless stiff-
ness K and the core energy E
c
of vortices. The stiff-
ness is related to n
s
K(T)=
2
k
B
T
n
s
(T)
m
∗
d
4
, (23.135)
Fig. 23.55. Results for the superfluid density divided by m
in units 10
−2
m
−1
e
Å
−2
as a function of temperature T for var-
ious doping concentrations: x =0.155 (squares), x =0.122
(diamon ds), x =0.091 (circles). T
c
is given as indicated
by the intersection of n
s
(x, T)withaT,where1/a = /2
(BKT theory)
where d is the average spacing between neighboring
CuO
2
-planes. Hence, T
c
∼ n
s
(T
c
)K(T
c
)andK(T
c
)
is given by BKT. Starting from the smallest vortex–
antivortex pairs of size r
0
,the pairs are integrated out
and their effect is incorporated by an approximate
renormalization of K and the fugacity y = e
−E
c
/k
B
T
.
As mentioned earlier this leads to the Kosterlitz re-
cursion relation [92]
dy
dl
=(2−K)y , (23.136)
dK
dl
=−4
3
y
2
K
2
, (23.137)
where l =ln(r/r
0
) is a logarithmic length scale.
Bound pairs reduce K and thus n
s
,butdonotde-
stroy superconductivity.At T
c
, K jumps from a uni-
versal value of 2/ to zero. The values of T
c
shown
in Fig. 23.56 are obtained by numerically integrating
(23.137) with n
s
taken from FLEX results.
In Fig. 23.56 we plot results by Timm et al. for the
transition temperature T
c
obtained with the help of
BKT theory and the temperature T
∗
c
where Cooper-
pairs form. For decreasing doping x, T
∗
c
becomes
nearly constant and decreases slightly for the lowest
doping level, consistent with the strong decrease of
the onset temperature of vortex effects at even lower
doping. On the other hand, T
c
decreases again in the
1480 D. Manske,I. Eremin, and K.H.Bennemann
Fig. 23.56. Calculated doping dependence for T
c
calcu-
lated by C. Timm et al. with the help of the Berezinski–
Kosterlitz–Thouless (BKT) theory. For comparison the T
c
curves obtained within 2D and 3D-XY models, and also
the mean-field result T
∗
c
are displayed
underdoped regime. We have also calculated the su-
perconducting gap
0
extrapolated to T → 0 (not
shown).
0
is here defined as half the peak-to-peak
separation in the density of states. We find approxi-
mately
0
≈ T
∗
c
. For a comparison the T
c
curves ob-
tained within 2D and 3D XY models are also shown.
We again find that Cooper-pair phase fluctuations
are unimportant in the overdoped regime. Note that
n
s
(T, x) → 0forT → T
∗
c
, since Cooper-pairs disap-
pear at T
∗
c
.
The transition temperature T
c
has to be deter-
mined by averaging over the Cooper-pair phase fluc-
tuations. In a Ginzburg–Landau (GL) treatment the
phase is given by the GL wave function (r, t)=
| |e
i(r,t)
,wheren
s
is related to the correlation func-
tion ∇(r, t) ·∇(0, 0). In the presence of spatial
phase fluctuations of (r) the averaged superfluid
density ¯n
s
= |¯ (r)|
2
∇(r) ·∇(0) will vanish at T
c
so that no Meißner effect occurs above T
c
.BKTthe-
oryaswellasthe2Dand3D-XY models[147] predict
that T
c
is proportional to n
s
(T
c
)/m.Notethat T
c
as
obtained within the 3D-XY model is larger than the
2D values,since fluctuationsareless important in 3D.
Finally, we calculate the dynamical phase stiffness.
Note that the superfluid density can be obtainedfrom
the imaginary part of the conductivity
n
s
m
∗
=
1
e
2
lim
!→0
!
S
2
(!) . (23.138)
Fig. 23.57. Frequency dependent phase stiffness n
s
(!)/m
∗
for doping x =0.12 (underdoped) and various tempera-
tures k
B
T/t =0.012,0.015, 0.016,0.017,0.018, 0.019, 0.0195,
0.02, 0.0205, 0.021, 0.0215, 0.022, 0.0225, 0.023 (with de-
creasing n
s
(0)/m
∗
). Here, t = 250 meV is the hopping
integral. The frequency is given in units of t ( =1).At
T
∗
c
≈ 0.023t/k
B
= 66.5 K, Cooper-pairs start to form. Be-
low T
∗
c
there is a marked transfer of weight from energies
above 2
0
to energies below, where
0
is the maximum gap
at low temperatures as obtained from the FLEX calcula-
tions
This can be shown with the help of Kramers–Kronig
relations. We have recalculated n
s
/m
∗
in this way
and find results identical to those obtained from
(23.51). Note that for the small wave vector q → 0
the (23.138) can be written as [92]
n
s
(!)
m
∗
=
1
e
2
!
S
2
(!)
!→0
. (23.139)
The imaginary part
S
2
(!)ofthedynamicalcon-
ductivity is obtained from the FLEX approximation
for the dynamical current–current correlation func-
tion using the Kubo formula. This is discussed in
Appendix D.
Notethat itfollowsimmediatelyfrom (23.139)that
n
s
= A
DC
T
c
with A =
m
∗
e
2
(!
s
2
/
DC
T
c
)
!→0,T→T
c
.
The resulting phase stiffness n
s
(!)/m
∗
is shown
in Fig. 23.57 for x =0.12 (underdoped) at vari-
ous temperatures. At higher doping the results (not
shown) are similar, only the typical frequency scale,

23 Electronic Theory for Superconductivity 1481
whichturns outto be the low-temperature supercon-
ducting gap
0
, is reduced. For temperatures T < T
∗
c
the superfluid density is non-zero at ! =0,indi-
cating the presence of the Cooper-pair phase fluc-
tuations in the system. On the contrary, for T = T
∗
c
n
s
(! =0)/m
∗
= 0 and thus no dynamical Cooper-
pair phase fluctuations are present. Note that for
! > 0 the superfluid density is finite even for
T > T
∗
c
. At at a first glance this is surprising, since
the phase is not well-defined for = 0. However, the
corresponding action of the Cooper-pair phases also
contains a contribution from the time derivative of
the phase besides the stiffness term. While the total
action vanishes, each term on its own does not. An-
other interesting observation is that all curves merge
together at energies of about 2
0
.Thisisexpected,
since the superfluid density is a current–current cor-
relation function, which has a characteristic energy
scale at about 2
0
in the superconducting state.
Even slightly below T
∗
c
, n
s
(! =0)/m
∗
obtains a
significant finite value, leading to the Meissner ef-
fect, and there is a considerable redistribution of
weight from energies roughly above twice the low-
temperature gap, 2
0
, to energies below 2
0
.Thisre-
distribution increases with decreasing temperature.
Also, a peak develops slightly below
0
followed by
adiparound2
0
,thisstructurebeingmostpro-
nounced in the underdoped case. Since
0
is smaller
in the overdoped regime, n
s
(!)/m
∗
changes more
rapidly for small ! in this case. Of course it is not
surprising that 2
0
is the characteristic frequency
of changes in n
s
(!)/m
∗
related to the formation of
Cooper-pairs.
To summarize, we have analyzed the behavior of
the superfluid density n
s
(!, T, x), which controls
the doping dependence of the phase coherence, the
thermodynamic behavior, the penetration depth, the
Nernst effect, Cooper-pair phase fluctuations, etc.
Note that we find that the superfluid density plays
the most significant role in the underdoped cuprates
and determines the superconductivity. We find our
results to be consistent with the BKT theory.Also the
recently noted universal scaling relation by Homes
n
s
∝
DC
T
c
(23.140)
in hole-doped and electron-doped superconductors,
in which the dc conductivity
DC
is measured ap-
proximately at T = T
c
[97], is contained in the gen-
eral expression for n
s
. We immediately obtain in the
underdoped high-T
c
cuprates
n
s
(T =0)∝
DC
(T = T
c
) T
c
, (23.141)
asobservedin experiment.Notethat(23.139) is taken
in the limit T → 0 assuming a thermodynami-
cal phase transition and Fermi liquid-like behavior.
However, in the case that quantum fluctuations are
important close to T = 0,the simple formof (23.139)
is no longer valid because of logarithmic correction
terms [148–150].
Another interesting question in cuprates is
whether there exists a quantum critical point (QCP)
at around x =0.19 doping concentration. The QCP
should be reflected characteristically by a universal
behavior of some physical properties such as the op-
tical conductivity (independent of time and length
scales). A possible interplay of QCP and thermody-
namical points needs further study.
23.4.8 SIS and NIS Tunneling Spectra
Tunneling spectra are a good measure of the
superconducting state and the elementary exci-
tations in general. They shed light on the va-
lidity of our electronic theory. Here, we calcu-
late the tunneling spectra for SIS (superconductor/
insulator/superconductor) and NIS (normal-state
metal/insulator/superconductor).Letus see to which
extent the spin fluctuation model for superconduc-
tivity can explain the fine structures seen by tunnel-
ing spectroscopy below T
c
in the cuprates (remem-
ber the significant success of the BCS and Eliash-
berg theory of superconductivity due to electron–
phonon coupling resulting from the explanation of
the fine structures seen by tunneling spectroscopy
in conventional superconductors,which exhibits the
single-particle excitations spectrum [50]). It is im-
portant to relate these features to the spin fluctu-
ation frequency !
sf
and resonance frequency !
res
.
One expects that the remarkable dip structure seen
in the single-particle excitation spectrum of vari-
ous cuprates might be an intrinsic fingerprint of a
