Bennemann K.H., Ketterson J.B. Superconductivity: Volume 1: Conventional and Unconventional Superconductors; Volume 2: Novel Superconductors

Подождите немного. Документ загружается.

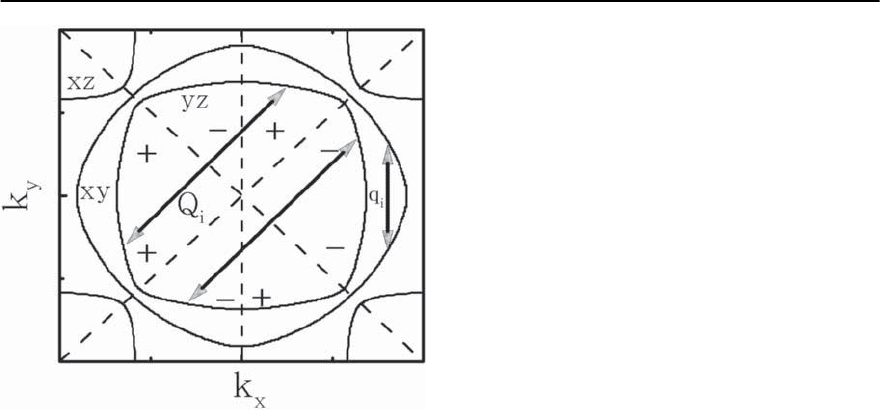
1492 D. Manske,I. Eremin, and K.H.Bennemann

Fig. 23.71. Symmetry analysis of the order parameter for

triplet pairing with | m |= 1 in the first BZ for k

=0.The

wave vectors Q

and q

arethepronouncedwavevectors

resulting from the susceptibility (without spin–orbit cou-

pling). For f

−y

2 -wave symmetry the nodes of the real part

of the order parameter are shown (dashed lines)andthe

regions +(–) where the f

−y

2 -wave superconducting gap is

positive (negative). Note that for the real part of a p-wave

order parameter the node would occur only along k

opposite and equal sign. Therefore, for the xy-band

we get no solution with f

−y

-wave symmetry. On

the other hand, for the xz and yz-bands the wave

vector Q

bridges portions of the FS with equal signs

of the f

−y

-superconducting order parameter. The

eigenvalue of this order parameter is also enhanced

due the interband nesting for xz and yz-bands. Thus,

superconductivity in the xz and yz-bands in the

RuO

plane would be possible with the f

−y

-wave

order parameter. Therefore, solving (23.144) for the

three-band picture we found a competition between

triplet p-wave and f

−y

-wave superconductivity in

the RuO

-plane.

Also using (23.147) we can rule outsinglet pairing.

In particular,assuming d

−y

-symmetry for Sr

RuO

(23.144)yields an eigenvalue that is lower than in the

case of triplet pairing.As can be seen using Fig.23.71

this is plausible. Note that for d

−y

-wave symme-

try we get a change of sign of the order parameter

upon crossing the diagonals of the BZ. According to

(23.144)wavevectorsaroundQ

connecting areas(+)

and(–) contribute constructivelyto thepairing.Con-

tributions due to q

and the background connecting

areas with the same sign would subtract from the

pairing (see Fig. 23.71 with nodes at the diagonals).

Therefore, we get that the four contributions due to

in the xy-band do not allow to have d

−y

-wave

symmetry in the xy-band. Despite the pair-building

contributiondue to Q

one gets that the eigenvalue of

the d

−y

-wave symmetry in the xy-band is smaller

than for the f

−y

-wave symmetry. This is due to the

large contributionfrom Q

to the cross-terms for the

triplet pairing,which are absent for the singlet pair-

ing.For d

-symmetrywherethenodesarealongthe

(,0) and (0,)-directions we argue similarly. Thus,

we may exclude this symmetry. We safely conclude

that as a result of the topology of the FS and the spin

susceptibilityfor p and f -wave symmetry we seem to

get the strongest pairing. We can definitely exclude

d-wave pairing in the RuO

-plane.

Since we have found a strong competition be-

tween p-wave and f

−y

-wave superconductivity in

the RuO

-plane the question arises as to what is the

role of the c-axis in determining the superconduct-

ingproperties in Sr

RuO

.Doesthisquestionrequire

an understanding of the role of spin–orbit coupling

for the determining the symmetry of the supercon-

ducting order parameter?

First, the spin–orbit coupling affects the spin

dynamics and as we have shown induces the

anisotropy in the spin subspace. In particular, the

two-dimensional IAF at Q

=(2/3, 2/3) align

along the c-direction.Thissimply means that the an-

tiferromagnetic moments associated with these ﬂuc-

tuations align along the z-direction.At the same time

the ferromagnetic ﬂuctuations are in the ab-plane.

Since the interaction in the RuO

-plane (k

=0) is

mainly ferromagnetic nodeless p-wave pairing is in-

deedpossible and the superconducting order param-

eter in all three bands will not have nodes and not

only forxy -band as before. Notealso that the  -band

reveals a high density of states. Therefore, the triplet

p-wave pairing without line-nodes will be realized in

the RuO

-plane.

On the other hand, the state between the RuO

plane will be determined mainly by the IAF that

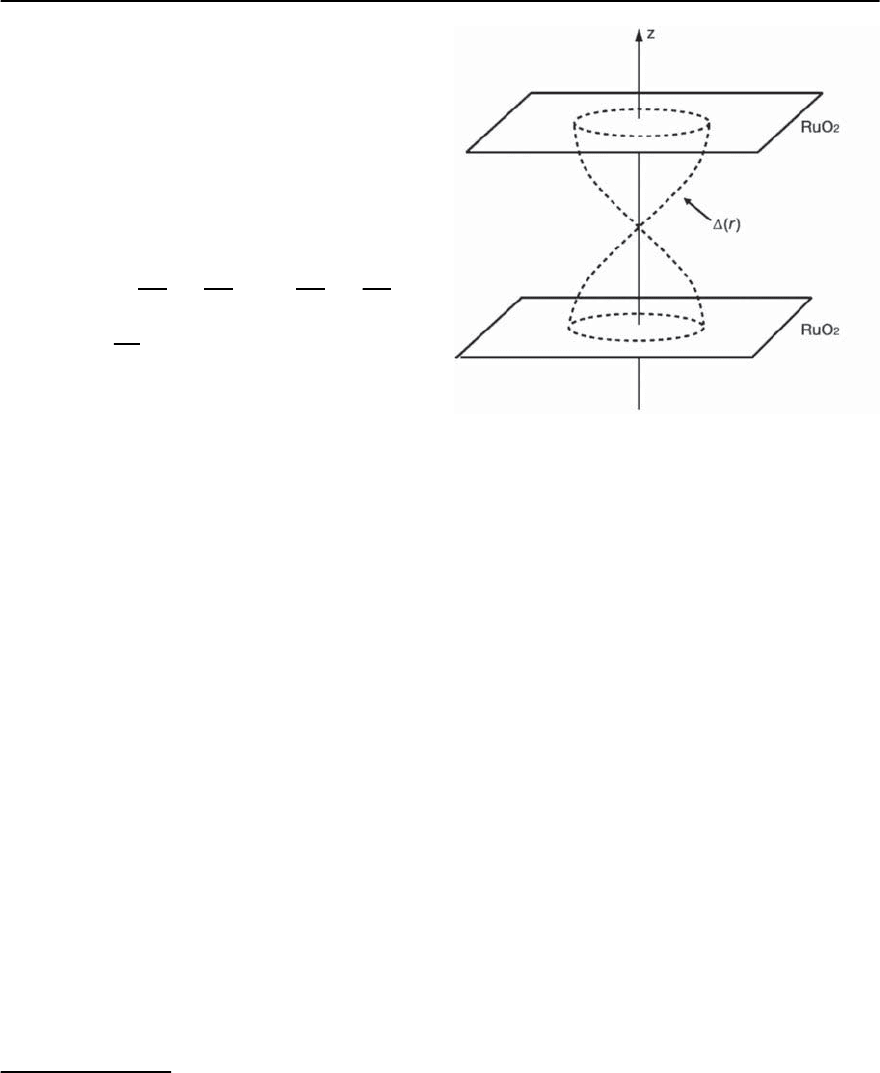
23 Electronic Theory for Superconductivity 1493

are polarized along the c-direction. This implies that

the magnetic interaction between the planes has

to be rather antiferromagnetic than ferromagnetic.

This antiferromagnetic interaction suggests a line

of nodes for (k) between the neighboring RuO

planes. In a phenomenological approach this was

shown by two groups [169–171]. For example, it was

proposed that the symmetry of the superconducting

order parameter in Sr

RuO

will have the form



= 

˜z



sin

cos

+ i sin

cos



×cos

. (23.150)

Then, due to the magnetic anisotropy induced by

spin–orbit coupling a nodeless p-wave pairing is

possible in the RuO

-plane, as observed experimen-

tally [168]. Thus, a node would lie between the

RuO

-planes. This is illustrated in Fig. 23.72. Indeed

as observed by thermal conductivity measurements

[168,169], the nodes in the superconducting order

parameter are between the RuO

-planes.

Note that the spin–orbit coupling also determines

the orientation of the orbital moment of the Cooper-

pair. In particular, it is convenient to combine the

threespin component into a vector d(k)inspinspace.

As mentioned earlier this is achieved by the expand-

ing 

in the three symmetric 2 × 2matricesi





 =1, 2, 3, where 



are the Pauli matrices as





(k)(



i



−d

+ id



(23.151)

Then, in a triplet superconductor, the pairing state

can be represented by the three-dimensional vec-

tor d(k), whose magnitude and direction may vary

over the Fermi surface in k-space. Like in

He several

pairing states related to the different orientation of

the total spin moment of the Cooper-pair d

, d

mayhavethesamecondensationenergyunderweak-

coupling conditions.This degeneracy is related to the

spin rotation symmetry being present in

He (which

Fig. 23.72. Schematic representation of the possible node

formation in the order parameter between the RuO

planes (in real coordinate representation) as resulting from

the magnetic anisotropy. Here, the amplitude of the or-

der parameter along the z-direction has been drawn in

cylindrical coordinates between RuO

-planes. This seems

in agreement with thermal conductivity measurements be-

low T

[168,169]

leads to the presence of a so-called B-phase), but this

is lifted by the spin–orbit coupling in Sr

RuO

[108].

Thus, the analogy of the A-phase in

He occurs in

RuO

(d(k)

= (0,0,d

± ik

))), while the B-

phase might be suppressed (d(k)

=(d

, d

, 0)).

This B-phase corresponds to S

=0.Asonecansee

from (23.106), we get that the transverse susceptibil-

ity and thus V

+−

is larger than V

for q  0(see

Fig. 23.67).

ThistendstosuppresstheB-phase.

The different orientation of the spin and orbital

angular momenta of the Cooper-pair is illustrated

in Fig. 23.73. The important consequence of this or-

der parameter is the uncompensated orbital angular

momentum of the Cooper-pair (the so-called “chi-

ral” state). Why is the chiral state (k)=d

(sin k

i sin k

) realized? To understand this, one has to con-

sider the additional contribution of the spin–orbit

coupling (l

·s) to the free energy in the supercon-

We note that for the sake of simplicity the momentum dependence of the gap function was illustrated in the previous

sections by the use of (23.104),which correspondsto | m |= 1 rather than (23.106),which requires a more sophisticated

analysis.

1494 D. Manske,I. Eremin, and K.H.Bennemann

Fig. 23.73. Illustration of the possiblesuperconducting states in Sr

RuO

taken from [172].Spin and total angular momen-

tum for (a) (k)=d

(sin k

+i sin k

)and(b) (k)=d

sin k

sink

.The(k)=d

(sin k

+i sink

) superconducting

state has an angular momentum along the c-axis (thick arrow) and the spin lying in the RuO

-plane. Note that the chiral

state displayed in (a) is obtained from our eigenvalue analysis

ducting state. Here, l

refers to the orbital moment

of a Cooper-pair and s denotes the electron spin.

In a simple mean-field analysis the components of

s are replaced by s

∼

· H

where 

refers to

the transversal (

+−

) and longitudinal (

)compo-

nent of the magnetic susceptibility.Obviously,dueto



> 

+−

(see Figs. 23.67 and 23.68) the degener-

acy of the states (k) is lifted, since one gains more

energy if the orbital moment of a Cooper-pairs is

aligned along the z-direction. Thus, the chiral state

has the lowest energy [108,171].

In analogy to

He, interesting effects can be ob-

served by applying an external magnetic field or ex-

ternal pressure along ab-plane to Sr

RuO

.Forex-

ample, in

He under pressure the transition from B

to A phase has been observed. In Sr

RuO

the situ-

ation is the opposite. Superconductivity in Sr

RuO

is already in the A-like phase and therefore, by ap-

plying pressure or magnetic field one could cause

the transition into B-like phase. However, if the  -

band becomes more nested due to external pressure,

an f -wave order parameter is possible. Another in-

teresting effect concerns the possible change of the

orientation of the unit vector d

= ˆz of the super-

conducting order parameter induced by the external

magnetic field discussed in Sect. 23.3.5. This means

that for a relatively large magnetic field applied along

the c-directionthe significant d

and d

components

in the superconducting order parameter in Sr

RuO

can be induced. Of course, this effect is relatively

small (as also in

He)butcanbeobserved.

In summary,Sr

RuO

is a remarkable exampleof a

system where the interplay of ferromagnetic and in-

commensurate antiferromagnetic ﬂuctuations may

result in a non-trivial symmetry of the supercon-

ducting order parameter. Note that the nesting of ˛

and ˇ-bands may, as we have shown, lead to a node

formation in the superconducting gap. Although its

existence has not yet been definitely concluded ex-

perimentally it can be verified by applying a mag-

netic field or pressure. Since the antiferromagnetic

ﬂuctuations are not helpful for the triplet pairing,

one may expect an enhancement of the supercon-

ducting transition temperature and the nodeless su-

perconducting gap if the nesting is suppressed. In-

terestingly, this phenomenon was proposed to be

responsible for the occurrence of superconductivity

in the ferromagnetic phase [173] of unconventional

superconductors like ZrZn

and UGe

. In particu-

lar, we have shown that spin–orbit coupling plays

an essential role in stabilization of the A-like phase

in Sr

RuO

and might be responsible for the pos-

sible node formation between neighboring RuO

planes.

23.5.5 Doping Dependence of Ruthenates

Comparing ruthenates and cuprates one can clearly

see that their behavior differs drastically in the nor-

mal state. The ruthenates are good Fermi-liquid

systems despite of the presence of IAF at Q

(2/3, 2/3). On the other hand, cuprates can be

characterized as systems that may behave mainly

non-Fermi-liquid-like. The most remarkable is the

doping concentration dependence of the cuprates

properties. The electronic correlations are more im-

portant in cuprates. The on-site Coulomb repulsion

U (which can be roughly estimated as e

/r where r

refers to the radius of the corresponding electronic

shell) is much larger than the bandwidth. In the

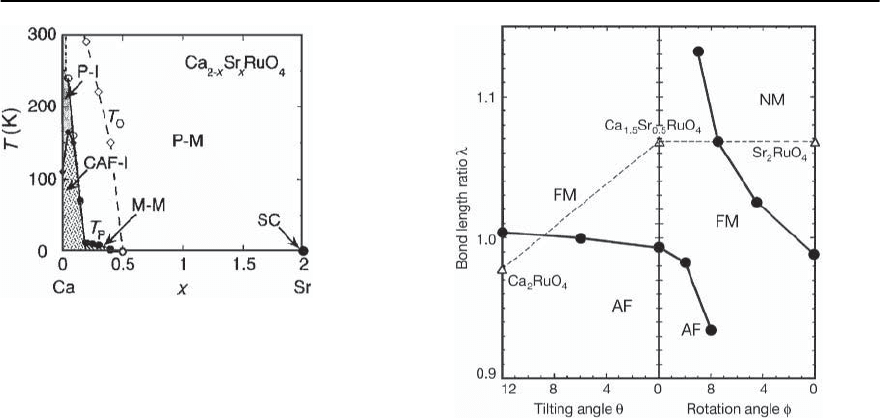
23 Electronic Theory for Superconductivity 1495

Fig. 23.74. Phase diagram of Ca

2−x

RuO

.P refers to para-

magnetic,CAFto cantedantiferromagnetic,M to magnetic,

SC to the superconducting phase,–M to the metallic phase,

and –I to the insulating phase

ruthenates that are 4d-electron systems the effect of

correlations is weaker than in cuprates and U is of

order of the electronic bandwidth,W. Therefore,one

concludes that in ruthenates we are in the interme-

diate correlation regime. As a result, in the ruthen-

ates the correlations are not strong enough to violate

Fermi-liquid theory.Nevertheless,correlations in the

ruthenates also occur.Thisis obviousfrom Fig.23.74.

In Fig. 23.74 we show results for the magnetic

phase diagram obtained experimentally by Nakat-

suji and Maeno [174] for Ca

2−x

RuO

. Despite the

fact that introducing Ca does not change the valence

in the system the magnetic phase diagram changes

completely. First, superconductivity disappears and

systems remain paramagnetic metals up to x =0.5.

Then, the system becomes a ferromagnetic metal.

Most remarkably, upon further doping an insulating

antiferromagnetic transition occurs.

Note that introducing a Ca instead of an Sr ion al-

lows to have structural distortion of the pure tetrag-

onal crystal lattice of Sr

RuO

due to the smaller ra-

dius of the Ca ionic sphere. This was discussed by

Fang and Terakura [175] by means of LDA calcu-

lations. Their main results are shown in Fig. 23.75.

First, between 0 < x < 0.5theRuO

octahedra gets

rotated around the c-axis. This basically changes the

hopping term of the xy-band and most importantly

brings the van Hove singularity closer to the Fermi

level enhancing the ferromagnetic ﬂuctuations and

leading to a ferromagnetic state at x =0.5. Further

Fig. 23.75. The calculated magnetic phase diagram of

RuO

including structural distortions,taken from [175].

The solid lines are calculated phase boundaries, while the

triangles linked by dashed lines correspond to the experi-

mental data

doping with Ca allows one to have not only the rota-

tion of the RuO

octahedra, but also its tilting. Thus,

hopping in the xz and yz-bands reduces. As a con-

sequence, the Coulomb repulsion U will be larger

than the bandwidth of the conduction bands.The re-

sulting increase of correlations cause a Mott insula-

tor transition driven by the IAF ﬂuctuations. Further

studies of the resistivity in Ca doped samples will

justify the proposed scenario.

Summary

To summarize in this section we have studied triplet

superconductivity. Sr

RuO

is a solid state system

for which unconventional triplet superconductiv-

ity may occur. We have shown that spin ﬂuctua-

tions may explain qualitatively the occurrence of p-

wave superconductivity with line nodes between the

RuO

-planes. Furthermore, due to the presence of

ferromagnetic and incommensurate antiferromag-

netic ﬂuctuations Sr

RuO

seems to be an ideal sys-

tem where the role and competitions of various spin

ﬂuctuations for the formation of superconductivity

can be studied in detail. In particular, we have seen

1496 D. Manske,I. Eremin, and K.H.Bennemann

that incommensurate antiferromagnetic spin ﬂuctu-

ations are not helpful for triplet pairing and may re-

sultin theformation of line nodesbetween neighbor-

ing RuO

-planes. The relative simplicity of this com-

pound in comparison to heavy-fermion supercon-

ductors could make Sr

RuO

the model system where

further interesting and exciting physics (in partic-

ular regarding thermodynamical properties, effects

due to magnetic and non-magnetic impurities, etc.)

will be discovered.

23.6 Summary and Outlook

In this review we present a microscopic theory us-

ing a model Hamiltonian for the interactionbetween

quasiparticles and spin ﬂuctuations. This is applied

to the layered cuprates and Sr

RuO

.Forsimplic-

ity we assume that the electronic dynamics is es-

sentially controlled by the CuO

and RuO

-planes,

respectively.

For the description of singlet superconductivity in

the cuprates we employ a one-band model Hamilto-

nian.The interaction between the carriers (quasipar-

ticles) is described by an effective Coulomb coupling

U and the itinerancy of the carriers by a hopping in-

tegral t.In the case of hole doping the states of the ef-

fective band are mainly the hybridized p-states origi-

nating from the O-atoms.The spin ﬂuctuations arise

from the magnetic activity of the Cu-spins and the

induced spin polarization of the p-states. In the case

of electron doping the effective one-band Hamilto-

nian describes the hybridized d-states of the UHB

and U is an effective coupling between the electrons

in these states. The spin ﬂuctuations result from the

Cu-spins. Upon doping the Cu-spins are quenched

and the spin polarization of the band is reduced. We

assume itinerant magnetism for the carriers in the

UHB.

Using this model we have found that the phase di-

agram, the symmetry of the superconducting order

parameter, and the behavior of the elementary and

spin excitations in hole-doped and electron-doped

cuprates can be largely understood.We have found a

particularly interesting behavior forthe underdoped

cuprates. (Note, however, that for smaller doping our

theory needs to be extended.) Due to strong scatter-

ing of quasiparticles by antiferromagnetic spin ﬂuc-

tuations a “weak” pseudogap appears at the Fermi

level in the density of states. It increases with de-

creasing doping concentration. The spectral density

has different weightsfor holesand electrons.Cooper-

pair phase ﬂuctuations in underdoped cuprates are

enhanced by the reduced dimensionality and also

since phase-incoherent Cooper-pairs do not over-

lap well, resulting in a small n

. These ﬂuctuations

of phase-incoherent Cooper-pairs destroy the long-

range superconducting order and the Meissner ef-

fect. In conventional bulk superconductors this is

not relevant, since the large superﬂuid density leads

to a typical energy scale of phase ﬂuctuations much

larger than the superconducting energy gap  that

governs the thermal breaking of Cooper-pairs. Thus,

in conventional superconductors the superconduct-

ingtransitionisduetothe destructionof the Cooper-

pairs and T

is proportional to 

.Wehavefound

∝ n

in underdoped hole-doped cuprates indicat-

ing that the phase ﬂuctuations drive the transition.

The Cooper-pairs only break up at a crossover tem-

perature around T

∗

, T

∗

> T

. T

∗

is approximately

givenbythe transitiontemperature onewouldobtain

without phase ﬂuctuations. Between T

and T

∗

local

Cooper-pairs without long-range phase coherence

may be present. Therefore, we conclude that we may

have a qualitative understanding of the phase dia-

gram in the cuprates. Furthermore,the important el-

ementary excitations and their interdependence with

spin excitations (resonance peak) can be well under-

stood within our theory. Our results also shed light

on the asymmetry of hole-doped and electron-doped

cuprates.

For describing triplet Cooper-pairing in Sr

RuO

we also employ a Hubbard Hamiltonian. In order to

derive an electronic theory we take the electronic

band structure of Sr

RuO

into account. Magnetic

activity arises from the itinerant electrons in the

Ru d-orbitals. Due to spin–orbit coupling a strong

magnetic anisotropy occurs (

+−

< 

)inthenor-

mal state. This mainly results from different values

of the g-factor for the transverse and longitudinal

components of the spin susceptibility (i.e. the ma-

trix elements differ) and from a change of the bare

energy dispersion of the d-electrons. Obviously,this

23 Electronic Theory for Superconductivity 1497

and the presence of incommensurate antiferromag-

netic and ferromagnetic ﬂuctuations have conse-

quences for the symmetry of thesuperconducting or-

der parameter. In particular, using spin-ﬂuctuation-

induced Cooper-pairing one can understand how p-

wave Cooper-pairing with line nodesbetween neigh-

boringRuO

-planes may occur.

Despite the relative success of the Eliashberg-like

treatment of superconductivityvia spin ﬂuctuations

exchange in cuprates and ruthenates there remain

critical questions. In particular, in the theory of

cuprates it is necessary to clarify the role ofthe vertex

corrections and to which extent an effective second-

order perturbation theory canbe applied.It might be

useful to take the original Hamiltonian referring to

Cu-spins and polarized p-states at oxygen sites and

derive the magnetic activity (spin-susceptibility,sta-

bility of local Cu-spins,etc.) and the itinerancy of the

carriers. Also canonical transformation theory and

slave-boson type theory should be used as alternative

treatments. In the underdoped cuprates the origin

of the pseudogap and the coexistence of short-range

weak antiferromagnetismand superconductivity has

to be understood. Also the symmetry of the super-

conducting order parameter in overdoped electron-

doped cuprates must be clarified. In the ruthenates

the thermodynamical properties remain to be stud-

ied in detail. It is of interest to apply our theory also

to superconductivity in heavy-fermion systems ex-

hibiting spin ﬂuctuations as well.

Appendix A:

Derivation of the Generalized Eliashberg

Equations for the Interaction of Quasiparticles

and Spin Fluctuations

Here, we present the derivation of the generalized

Eliashberg equations for the interaction of quasi-

particles and spin ﬂuctuations in a detailed form,

however, without discussing the relevancy of the ap-

proximations we used. This is discussed in the main

text [176–179].

We start with Green’s function for itinerant elec-

trons (holes). Using the Nambu notation for the su-

perconducting state [69], the one-particle Green’s

function is a 2 ×2-matrix

G(k, i!



d e



G(k, ) , (23.152)

where

G(k, )=−T



()

†

(0),

()=



k↑

()

†

−k↓

()



. (23.153)

We employ the Heisenberg picture:

k

() ≡ e

H

k

−H

, (23.154)

and

¯c

k

() ≡ e

H

†

k

−H

, (23.155)

where  corresponds to an imaginary time. Thus,

we define the matrix elements of the one-particle

Green’s functions as

˛ˇ

(k,  )=−T



k˛

()c

†

kˇ

,

˛ˇ

(k,  )=−T



¯c

−k˛

()c

−kˇ

,

˛ˇ

(k,  )=−T



k˛

()c

−kˇ

,

˛ˇ

(k,  )=−T



¯c

−k˛

()c

†

kˇ

. (23.156)

In order to obtain the renormalized single-particle

Green’s function we solve the Dyson equation

−1

−

£ . (23.157)

This relates the matrix representing the bare propa-

gator

and its renormalization due to the sum of

all irreducible self-energy diagrams

£ to the dressed

propagator

G. The Dyson equation reads in Nambu

space

−1



−1

− £

−£

−

−1

−



, (23.158)

wheretheinversebarepropagatorisgivenby

−1

− 

. In the case where the effective pairing in-

teraction V

eff

isgivenbythediagramsshownin

Fig. 23.18 the self-energy is (for simplicity we put

1498 D. Manske,I. Eremin, and K.H.Bennemann

eff

= U)

(k, ı!

ˇN









(q, i

)

1+U

(q, i

)



(q, i

)

1−U

(q, i

)

+ U



(q, i

)



× G(k



, i!



) (23.159)

and

(k, ı!

)=−

ˇN









(q, i

)

1+U

(q, i

)

−



(q, i

)

1−U

(q, i

)

− U



(q, i

)



G(k



, i!



) ,

(23.160)

Here, i

= i!

−i!



and N denotes size of a square

lattice. The term U



G,F

on the right-hand side com-

pensates for double counting that occurs in second

order. £

and £

denote the normal and supercon-

ducting part of the self-energy, respectively [176].

and

correspondto the irreducible chargeand spin

susceptibility, respectively, and are given by



(q, i

)=−

ˇN



ki!

[

G(k + q, i!

+ i

)G(k, i!

)−

F(k + q, i!

+ i

†

(−k, i!

)



≡ 

(q, i

)−

(q, i

) (23.161)

and



(q, i

) ≡ 

(q, i

)+

(q, i

) . (23.162)

Note that on the RPA level also the charge ﬂuc-

tuations are included. This may be of interest if a

charge-density-wave (CDW) or stripe formation oc-

curs. Both may compete for small doping. For exam-

ple, it was pointed out that polarization-dependent

photoemission also reveals a fine-structure in thelow

energy excitation spectrum [75]. In particular, for

a single-layer high-T

superconductor at optimum

hole-doping two different behaviors of the spectral

density at (, 0) and (0, ) were found indicating

their difference. This may indicate the importance of

charge ﬂuctuations in cuprates.

Because Re £ is symmetric and Im £ is antisym-

metric with respect to i!

, it is possible to put:

(k, i!

)=i!

[

1−Z(k, i!

)

]

+ (k, i!

) ,

(23.163)

(k, i!

)=(k, i!

) , (23.164)

where Z and  are real and also symmetric with

respect to i!

. Z describes the renormalization of

the quasiparticle mass and  corresponds to the

renormalization of the bare band energy 

.This

will be also discussed in Appendix C. (k, i!

Z(k, i!

)(k, i!

) denotes the strong-coupling su-

perconducting gap function. In general, the interde-

pendence of elementary excitations with spin excita-

tions leads to strong self-energy effects. If lifetime

effects of the elementary excitations are included

the superconducting gap will also have a strong fre-

quency dependence.

Note that in the case where Cooper-pair phase

ﬂuctuations are unimportant one may choose

F(k, i!

)=e

2i˛

∗

(k, −i!

) (23.165)

and put the phase equal to zero.Thus,no extra equa-

tion occurs for

(k, i!

Then, with the help of (23.163) and (23.164) we

are able to write down the diagonal and off-diagonal

parts of the one-particle Green’s function [76]:

G(k, i!

Z(k, i!

)+

+ (k, i!

)

(

Z(k, i!

)

−





+ (k, i!

)



− 

(k, i!

)

(23.166)

F(k, i!

(k, i!

)

(

Z(k, i!

)

−





+ (k, i!

)



− 

(k, i!

)

(23.167)

Since we want to solve the generalized Eliashberg

equations on the real !-axis rather than on the Mat-

subara points on the imaginary axis, we now use the

23 Electronic Theory for Superconductivity 1499

spectral representation of the one-particle Green’s

function

G(k, i!

∞



−∞

N(k, !)

− !

F(k, i!

∞



−∞

(k, !)

− !

, (23.168)

and inserting (23.168) into (23.161)and (23.162).Af-

ter performing the sum over the Matsubara frequen-

cies [73] we arrive at

Im 

s0,c0

(q, !)=



∞



−∞





f (!



)−f (!



+ !)







N(k + q, !



+ !)N(k, !



)

× A

(k + q, !



+ !)A

(k, !



)



(23.169)

f denotes the Fermi distribution function.

Thus we arrive at the following set of equations

for the quasiparticle self-energy £



 =0,3,1inthe

Nambu representation:



(k, !)=N

−1





∞



d§



(k − k



, §)

+(ı

 0

+ ı

 3

− ı

 1

) P

(k − k



, §)



∞



−∞



I(!, §, !







, !



) .

(23.170)

These equations have been discussed in the main

text. Here, the spin and charge ﬂuctuation interac-

tions are given by

(

2

)

−1



3

− 





= 



1−U



−1

(23.171)

and

(

2

)

−1



3

− 





= 



1+U



−1

. (23.172)



was defined in (23.25). Then,

(k, !) Z (k, !)=

−

N





∞



d§



(k − k



, §)−P

(k − k



, §)



∞



−∞





f (−!



)+b(§)

! + iı − § − !



f (!



)+b(§)

! + iı + § − !





× Im



Z(k



, !



)(k



, !



)

D(k



, !



)



, (23.173)

! Z (k, !)=

−

N





∞



d§



(k − k



, §)+P

(k − k



, §)



∞



−∞





f (−!



)+b(§)

! + iı − § − !



f (!



)+b(§)

! + iı + § − !





× Im



Z(k



, !



D(k



, !



)



(23.174)

and



+ (k, !)=

−(N)

−1





∞



d§



(k − k



, §)+P

(k − k



, §)



∞



−∞





f (−!



)+b(§)

! + iı − § − !



f (!



)+b(§)

! + iı + § − !





× Im







+ (k



, !



)

D(k



, !



)



. (23.175)

Here, D(k, !)=

[

!Z(k, !)

]

[

(k, !)Z(k, !)

]

−





+ (k, !)



and b(!), f (!) are the Bose and

Fermi distribution functions, respectively.

These are the so-called generalized Eliashberg

equations on the real frequency axis. Their detailed

numerical solution will be discussed in Appendix B.

Note that in contrast to the electron–phonon case

the momentum dependence cannot be restricted to

the Fermi surface due to the strong anisotropy of the

elementary excitations and the pairing interaction.

1500 D. Manske,I. Eremin, and K.H.Bennemann

Appendix B:

Numerical Solution Method for the

Generalized Eliashberg Equations

We discuss the details of the algorithm for the nu-

merical solution of the Eliashberg equations. This is

helpful for the programming of the equations. The

expressions are presented line by line as they occur

in the main program. To achieve the highest accu-

racy we avoid continuation methods like the Pade-

approximation and solve the Eliashberg equation di-

rectly onthereal-frequency axis.First,onestarts with

the calculation of the imaginary part of the spin sus-

ceptibilities using the tight-binding unrenormalized

energy dispersion 

Im

(q, !)=





∞



−∞



f (!)−f (! + §)



N(k, !)

× N(k + q, ! + §) ,

(23.176)

Im

(q, !)=





∞



−∞



f (!)−f (! + §)



(k, !) A

(k + q, ! + §).

(23.177)

Then, we obtain their real parts via Kramers–Kronig

relation:

Re 

G,F

(q, !)=



∞



−∞

Im 

G,F

(q, !)

! − §

(23.178)

and define the irreducible charge and spin suscepti-

bilities



= 

− 

, 

= 

+ 

. (23.179)

In the next step we calculate the kernels of the Eliash-

berg equations:

≡







1−U



≡







1+U



, (23.180)

≡ P

+ P

−









+ 





, (23.181)

≡ −P









+ 





, (23.182)

and plug them into the equations for determining the

imaginary parts of the self-energies

Im(k, !)=





∞



−∞

d§



b(§)+f (§ − !)



(q, !)A

(k − q, ! − §)

(23.183)

and

Im£(k, !)=−





∞



−∞

d§



b(§)+f (§ − !)



(q, !)N(k − q, ! − §) .

(23.184)

The real parts are obtained again via Kramers–

Kronig relations:

Re (k, !)=



∞



−∞



Im (k, !



)



− !

, (23.185)

Re £

(k, !)=



∞



−∞



Im £

(k, !



)



− !

. (23.186)

The next step calculates the energy shift

 ≡



(k, !)+£

G∗

(k, −!)



, (23.187)

and the mass renormalization function

!Z ≡ ! −



(k, !)−£

G∗

(k, −!)



. (23.188)

This completes the first iteration.

23 Electronic Theory for Superconductivity 1501

Fig. 23.76. Illustration of the

procedure in order to solve

(23.170). The full momentum

and frequency dependence of

the quantities are kept. Thus,

our calculations include pair

breaking effects fortheCooper-

pairs resulting from lifetime ef-

fects of the elementary excita-

tions

With the obtained results for the energy shift and

the renormalization function we calculate the new

spectral densities

N(k, !)=−



!Z + 

+ 

(

)

−





+ 



− 

= A

(k, !)+A

(k, !) , (23.189)

(k, !)=−





(

)

−





+ 



− 

(23.190)

and then return to the (23.176). The procedure is re-

peated until the convergence is reached. The numer-

ical calculations are performed on a square lattice

with 256 × 256 points in the Brillouin zone and with

200 points on the real ! axis up to 16t with an al-

most logarithmic mesh.The full momentum and fre-

quency dependence of the quantities is kept.Thecon-

volutions in k space are carried out with fast Fourier

transforms.Ashavewementioned,therealpartsof

the susceptibilities, gap, and self-energy are calcu-

lated with the help of the Kramers–Kronig relations

(P denotes the corresponding principal value inte-

gration). The spectral functions A

, P

G,F

,Im,Im,

and Im 

G,F

are antisymmetric and the correspond-

ing real parts are symmetric with respect to !.Thus

the spectral function for the interacting electrons (or

holes) N(k, !) is separated into a symmetric part A

and an antisymmetric part A

(see (23.25)). The cor-

responding equations for the normal state can be

recovered by setting the off-diagonal terms of the

self-energy, , A

,and

, identically to zero.

For an illustration in Fig. 23.76 we show how

(23.170)–(23.172) are solved: One starts with a dy-

namical spin susceptibility (q, !) and constructs

the effective pairing interaction using (23.18). Then,

the strong-coupling gap equation for the supercon-

ducting order parameter (k, !) and the corre-

sponding Dyson equation G

−1

(k, !)=G

−1

(k, !)−

£(k, !) have to be solved,respectively.Having solved

these two equations one has new appropriate start-

ing input values for an electron propagator G.Thisis

again used to calculate . This procedure is repeated

until all equations are solved.

In order to determine the superconducting transi-

tion temperatureT

we solve the linearized gap equa-

tion, see (23.185):