Bemelmans J. et. al. (editor) Elliptic and Parabolic Problems: Rolduc and Gaeta 2001
Подождите немного. Документ загружается.

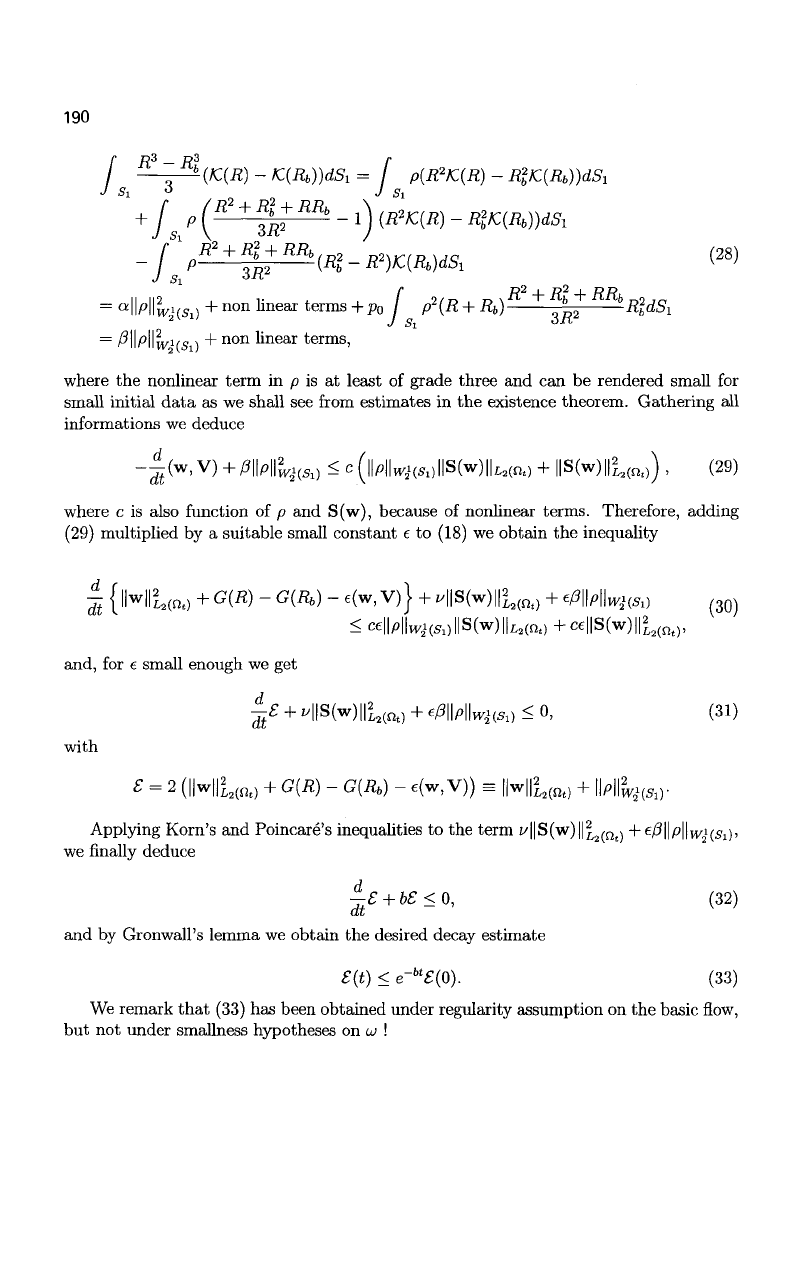
190
/
R
3
_ P
3
r
=—*(/C(/Z)
-
IC{R
b
))dS
l
=
/
p{R
2
K.{R)
-
RltCiR^dS,
Sl
2 2 '
1^
p
(
fl
+
f
R
t
RRb
~ l) (#£(*) -
RtlC(R
b
))dS_
p
R2
+ Rl
+
RRb
{Rl-tf)K{R
b
)dS, I.
2
T
-It-Hf,
, \ ,
,-,21--/
r>\ o2l-/
n njn
R*
+ Rl + RR
b
_ (28)
ft
3iP
2 _L i^„, f„™„,„. / „2fn , n.\
R2 +
R2
b
+
RR
t>
1
=
a
l|p||^
2
i
(5l
) + non linear terms +p
0
/
p
2
(.R + .R
6
)
^—
R\dSi
= P\\pW^i,
s
•.
+ non linear terms,
where the nonlinear term in p is at least of grade three and can be rendered small for
small initial data as we shall see from estimates in the existence theorem. Gathering all
informations we deduce
-|(w, V) +/?|M|^
1(Sl)
< c (||HI^(ft)IIS(w)|U
2(ni)
+ ||S(w)||i,
(nt)
) ,
(29)
where c is also function of p and S(w), because of nonlinear terms. Therefore, adding
(29) multiplied by a suitable small constant e to (18) we obtain the inequality
| {ll
w
IIL(n
t)
+ G(R)
-
G(R
b
)
-
e(w, V)} + H|S(w)|||
2(ni)
+ eP\\p\\
w
,
(Sl)
< ce||p||
W2
i(
Sl
)l|S(w)|U
2(f
2
t
) +ce||S(w)|||
2(nt)
,
(30)
and, for e small enough we get
Jt
with
£ + H|S(w)||!
2(nt)
+ eP\\p\\
wHSl)
< 0,
(31)
£ = 2 (l|w||i
2(ft[)
+ G(R)
-
G(R
b
)
-
e(w, V)) = ||w||£
2(nt)
+
|
11^(51)-
Applying Korn's and Poincare's inequahties to the term H|S(w)||w
n
>
+ ^IMIw'fSi)'
we finally deduce
^-S + bS < 0,
(32)
at
and by Gronwall's lemma we obtain the desired decay estimate
S(t) < e-
bt
£(0).
(33)
We remark that (33) has been obtained under regularity assumption on the basic flow,
but not under smallness hypotheses on
ui
!

191
6 Reduction to initial-boundary value problem in a
fixed domain
We intend to prove that if u satisfies the hypothesis of stability required by capillarity
theory, then for small perturbations of the rest state there exists a regular global solution
to (12) that decays exponentially to zero as time goes at infinity. To this end, in our proof
will play an essential role only smallness of perturbation, in this statement the gradient
of the basic shape is not infinitesimal ! For this reason the perturbation equation will
be linearized around basic flow carefully, say we write the equations in reference frame
rotating with angular velocity
u>
= oie
3
.
Of course, in Tt the velocity w is directly the perturbation to the rest, only we must
consider a suitable linearization of T
t
around i\. We remind that the surface r
(
is given
by the equation |x| = R(x/\x\,t) and the origin O coincides with the center of mass of
the liquid, i.e., J
n
x^ds = 0, k = 1,2,3. Assume that O
t
contains the ball BR^O) =
{|x| < R{\ and is contained in
R^R^O)
= {\x\ <
CQR\},
define a smooth function x(\
x
\)
such that x{\
x
\) = 0, if |x| < -Ri/2, xd^l) = 1) if W > -Ri.
an<
i consider the coordinate
transformation
—C
1
•*«©$-.))-•<••«.
(34)
or, in spherical coordinates
This transformation is invertible, if R
—
R
b
is not too large, and it maps Q
b
onto fi
(
and
T
t
onto V
b
leaving
B
Rl
/
2
invariant, and in some neighbourhood of I\ it holds : x = j^y.
Let J = (I
32
-) be the Jacobian matrix of the transformation y = y(x, t) inverse to
(34) and J = det J. It is clear that J is an inverse matrix to J
-1
= I
-£?•)
whose
V
' V°W/i,j=l,2,3
elements are easily calculated by differentiation of (34). The vector field u = Jw/J, with
w(j/,t) = -w(x(y,t),t), is solenoidal
2
and it holds
W
(x(y,t),t) = J(y,t)J-
1
(y,t)u(y,t)=J(y,t)u(y,t),
and

192
Hence :
w
t
= (ju)
t
- x(M)^Jff(y' J
T
v
H
)(J(y,t)u)
and the equations (22) take the form
Ju
t
+ J
(
u -
X
{\y\) o/./L',V(y
•
J
r
V,)(J(2/,i)u)
Wlwl)
+J(u
•
V,,) Ju -
v{3
T
V
y
•
J
T
Vj,)Ju + J
T
V,,r = -we
3
x ju,
V-u(y,t) = 0,
where r = p
—
p
b
, p = R
—
R
b
. The initial conditions are
u|
(=
o = u
0
{y) = J
0
w
0
,
p|
t=0
= po(y).
Further, we separate the tangential and the normal components in (22)3 which gives
Il
b
IlS{u, p)n = 0, -r + vn-S{u,p)n = K,{R)-]C(R
b
),
yeT
b
,
(35)
where nf = f
—
n(n
•
f) is a projection of the vector field f(x), x € F
t
, onto the tangent
plane to r
t
, (analogously for H
b
) and
<S(u,
p)
= J
T
V
®
Ju + (J
T
V
g>
Ju)
T
,
is a transformed matrix S(w) = V
<g>
w + (V ® w)
r
. We also transform the expression :
K,{R)-K,{R
b
) = a{H{R)-H(R
b
))+p
b
{R)-p
b
{R
b
), using the formula : U{R)-H{R
b
) =
n
•
A(i)x
—
ri;,
•
A
6
y, where A(t) and A
b
are Laplace-Beltrami operators on r
(
and T
b
,
respectively. We have K.(R) - IC(R
b
) = an
b
•
A
b
(p(y/\y\,t)e
r
) + T\ (p) + Ti (p), where :
Ji(p) = a((n-n
b
)-A{t)x + n
b
-(A(t)-A
b
)y)+p
b
{R)-p
b
(R
b
),
F
2
{p) = an
b
-{A(t)-A
b
)(e
r
p(y/\y\,t)).
We note in particular that the expression rif,- (A
:
(£)
—
A
2
(t)) y depends only on the
first derivatives of Rj and R2, because n
b
-dy/d^j = 0
(£1,
£2 are arbitrary local coordinates
on
Td)-
Therefore, Ti (p), i = 1,2 denote the sums of lower order and nonlinear terms with
respect to p, respectively. Let us consider kinematic boundary conditions. The normal
n (x(y, t)) to T
t
and the normal n^ to il
b
are related to each other by
»(*(*')) = |5 (36)
and in the neighbourhood of T
b
the elements of J are given by
Rbf-i ,
t
d (R
b
-R
6
>
+y
dy-\~R.
so,
J = (R
b
/R) . Therefore condition (22)
4
: (n
•
e
T
)R
t
(y,t) = w
•
n, is transformed into
Jij = -^6} + y'-.
n
„ Rl(y/\y\) „
n
,,,,*

193
Our free boundary problem reduces to the problem of finding
u(y,t),
r(y,t),
y e fl
b
,
and p{y,t), y e Si, satisfying the relations
J
Ut
+ J
4
U -
x{
\y\)PMMA
{
y . 3
T
V
y
)(3(y,t)u) + J(U
•
V,)Ju
-v(J
T
V
y
•
3
T
V
y
)Ju + J
T
Vj,r = -2we
3
x Ju,
V-u(y,t) = 0 yefl
b
,t>0,
n
6
nS(u, p)n = 0,
-r + vnS{u, p)n = K.{R) -
K.{R
b
),
R
2
(n
b
-e
T
)pt{y,i) = j±u-n
b
(y,t) y e Si,
u(y, 0) = 3(y, 0)v
0
(x(y, 0)) = u
0
(y) y € Q
b
,
p{y,
0)
= Ro(y) - R
b
{y) = p
0
{y) y £ F
b
,
(38)
or, which is the same
u
(
—
i/V
2
u + Vr = f (u, r,
p) —
2o;e
3
x u,
Vu = 0,
IL,S(u)n[, = II
6
b(u,p),
-r + vn
b
•
S(u)n(,
-cm
b
-
A
b
{p{y/\y\,t)e
r
) = d{u,p) + F{p),
n
b
•
e
r
p
t
= u
•
n
b
+ h(u, p)
u(2/,0) = u
0
(y)
p(y,o) = po(y)
(39)
2/
e r
6
, t > o,
y e Q
b
,
ye Si,
where
f(u,g,p)
(I - J)u
t
+ xM^/V'fhy
•
3
T
^
y
)(3(y,t)u) - J
t
u - J(u
•
V„)Ju
Mv/\y\)
= -2we
3
x (J - l)u + v ((J
r
V„
•
J
r
V„)Ju - V
2
)uJ + (I - J
T
)V.
b(u, p) = rif,S(u)ni, - ILS(u, p)n,
d(u,p) = v(n
b
-S(u)n
b
-n-S(u,p)n),
T(p) = T
1
{p)+^
2
(p),
(R?
h(u,p) = u-nJ-^-l
(40)
7 Existence theorem
In this section we prove Theorem 1.1. For this we need to consider the linear problem

194
(41)
v
t
-!/V
2
v + Vp = f(y,t),
V-v = 0,
n»S(v)ni =
b(y,t),
-p + vn
b
•
S(v)n
6
-crn
b
-
A
b
{p{y/\y\,t)e
T
) =
d(y,t),
n
b
•
e
r
p
t
= v
•
n
b
+ h(y, t) y£T
b
,t£
(0,
T),
v(y,0) = v
0
(y)
yeU
b
,
p(y,o) = Po(y)
yeS
u
with some given
i{y,t),
h(y,t), d(y,t), h(y,t).
Theorem 7.1 Let
f(y,t),
d(y,t),
h(y,t) be continuous in y, t, f(.,i) 6 C
a
(fl
b
), d e
C
1+a
{r
d
), h e C
2+a
{T
d
), Vi e (0,T), T < oo, b e
c
,1+a
-<
1+0!
>/
2
(rf
>
x (0,T)), v
0
e
C
2+a
(0
6
), po e C
3+a
(5i), and let the conditions
V-v
0
= 0, n
5
S(vo)n
6
|
Sl
=b(2/,0), b
•
n
b
= 0,
(42)
be satisfied. Then problem (41) has a unique solution p(.,t) e C
3+a
(5i), v(.,£) €
C
2+a
{tt
b
), p(-,i) £
C
1+a
(tt
b
)
withv
t
(;t) e
C
a
{Q
b
)
definedfort e (0,T), and this solution
satisfies the inequality
sup (\v
t
(.,t)\c°(si
b
) + |v(.,t)|cs+-(n,,) + b(-,*)|cJ+-(n
t
) + |p(-,<)|c^(
Sl
)
< c(T) (|v
0
|c
2
+»(n
t
) + |po|c
3
+«(Si) + |b(-,*)lc
1
+».(
1
+»>/
2
(r
b
x(o,r)))
+c(T)sup (|f(.,t)|c.
(
n,) + \d(,t)y+°(r
b
) + |A(-,*)lc+-(rJ -
(43)
where c(T) is a non-decreasing function ofT.
Proof.
Due to (41)
5
, the boundary condition (41)
4
can be written in the form
-p + vn
b
•
S(v)n
b
- an
b
•
/
Jo
v
•
n
b
+ h(y, T)
A
6
e
r
dr = an
b
•
A
b
e
r
p
0
(y) +
d(y,t),
n
b
-e
T
where
-p + vn
b
•
S(w)n
b
- an
b
•
/ A
b
w(y,r)dr + / Z
x
(w)dr
J 0 J 0
= am
•
A
6
e
r
p
0
(y) + d(y, t) + an
b
•
A r
'
A
b
-
0
n
6
'
e
r
dr.
Ji(v) = nf,
•
A
b
e
r
n
6
•
A
b
v,
a.
b
-e
r
is the first order differential operator applied to v. The solvability of the initial-boundary
value problem

195
v
t
-i/V
2
v + Vp = f(y,i)
yeSl
b
,t€(0,T),
V-v
= 0,
n
6
S(v)n
t
= b{y,t),
-p + vn
b
•
S(v)n
6
-o-ni
•
/ A
b
v{y,T)dr+ / h(v (y,r))dT = b(y,t)
Jo Jo
+ [ B{y,
T
)dT yer
b
,te{0,T),
J o
v(y,0) = v„(y) ye Slb,
(44)
and the estimate
sup {\vr
t
(;t)\c°(n,,) + \w(;t)\c*+°(n
b
) + |p(-,t)|c+»(n
6
))
t<T
< c(T) (|w
0
|c2+»(n,,) + |polc3+«(S!) + |ty^*)lci+°.(i+°)/2(r
t
x(o,r))) (45)
+c(T) sup (|f(-,0lo»(n,) + \b(;t)\c^(r
b
) + |S(-,t)|c-(r
t)
) ,
t<T
for the solution of this problem was established in [12]. It follows from (45) that the
solution of (41) satisfies the inequality
sup (|w((-,t)|
c
«
(
n
t
) + |w(-,t)|
C
2
+Q(fW
+ |p(-,t)|
C
i+«(«
6
))
t<T
<
c(T)
(|w
0
|
C
2+«(n
6
)
+
|po|c3+=(Si)
+
|b(-i*)lc
1
+«.(
1
+«)/
a
(r
b
x(o,T)))
+c(T) sup (|f(-,i)|
c
«(^) +
\d{;t)\c^
{
T
b)
+ \h(;t)\
C
2
+a(Tb)
).
Since p satisfies the elliptic equation (41)
4
on Si, Schauder's estimate yields the same
inequality for |p(-,t)|
C
3+«(
Sl
). The theorem is proved. •
Now, we turn our attention to the nonlinear problem (39). We start with the esti-
mation of the nonlinear functions (40) (major part of these estimates is obtained in ([7])
Let j(*' = (jjj\y,t)) be the Jacobian matrices of the transformations (34) with
R =
R
k
(y,t),
k = 1,2. The differences
J>}' —
j\f satisfy the inequalities
(2)
- ?
(1)
CH
.
(
„
b)
< c\
Pl
-
P2|o*«+-(tu)
k
=
0,1,2,
< c(\p
2t
-
Pw|c*+>+«(ni)
+
IPI
-
P2|c*+i+«(n
6
))
A;
=
0,1.
I
7
W
- 7
dt
(
'
3
*
J
'
c"=+»(n
b
)
In particular
:
\Jij>
— ^ij|c*+°(fi
b
)
^
c
lp|c*+»+»(ni,)
A;
=
0,1,2,
at^lc^tn,,)
-
c
(^'l
c
"
c+1+
'*(«i.)
+
l
p
l
c
"
!+1+<
"(^))
k = 0
>
1
-
The same inequahties hold for the elements of the matrices J(*',
(J^)
_1
,
as well as for
the functions j(*> = det
J(*>
and vector fields n<
fc)
defined in (36) with J = J
w
, k = 1,2

196
(but of course these vectors are evaluated on Tt). The coefficients of the difference of
the Laplace-Beltrami operators A^'(t)
—
A
(2)
(t) on the surfaces |x| = R
k
(x/\x\,t) can be
estimated in a similar way (see [12]). Omitting lengthy but elementary technical details
we present the estimates we are going to use below.
Lemma 7.2 //
Y
(
(u,r,p) ssup|u
s
(-,s)|c«(n
(
,)+sup|u(-,s)|
c
.
2
+»
(
n
l
)
s<t s<t
+ sup|r(-,s)|
C
i+«
(
n
b)
+sup|p(-,s)|
C
3
+
a
(
<
?l)
< n < 1, k = 1,2,
then
sup|f(u
2
,g
2
,P2) -f(ui,?i>Pi)|c-(n
b
) + |b(u
2
,p
2
) -b(u
1
,p
1
)|
c
.i
+
<,,(i+.)/2
(rbX(0it))
+ sup|d(u
2
,p
2
) -d(ui,pi)|
c
i+«(r
b
) + sup|/i(u
2
,p
2
) - ^(ui,Pi)lc
2
+»(r
b
)
d
+
SU
P ^(-^(Pz) - -^i(Pi))lci+»(r
t
) + sup \T
2
(p
2
) - ^2(pi)|c2+«(r
b
)
s<t Ot
s
<t
+ swp\ — {F
2
{P2) - ^2(pi))lc«(r,,)
s<t Ot
< criY
t
(u
2
-U!,r
2
- r
1}
p
2
- pi) + c|p
2(
- Pit|ci+°(r
b
)-
In particular, ifY
t
(\i,r,p) <n<l, then
sup |f (u, q, p)|c»(n
b
) + |b(u, p)|c+».(i+»)/2(r
t
x(o,t)) +
SU
P K
u
> P)|d+»(r
b
)
(46)
+ sup \h(u, p)|
C
2+»(r
b
) + sup
|(^(P)
!<*<">
-sup
at
v
+ sup|^
2
(p)|c2+«(r
b
)
c
i+°(r
b
)
s
<*
(47)
< cr?y
t
(u,r,p) + c|p
f
c«(r„)
ci+°(r
b
)-
These estimates and Theorem 7.1 enable us to prove that the problem (39) is uniquely
solvable in a finite time interval. We restrict ourselves to the case of small initial data.
Theorem 7.3 Assume that the datauo g C
2+a
(Q.
b
), p € C
3+a
(5i) satisfy the compatibil-
ity conditions V-u
0
= 0, II(,S(uo)n(,|r
6
= n
6
b(u
0
,po) and that |u
0
|c
2
+»(n
b
) + |Po|c
3
+'"(s
1
) <
E
< 1. Then, there exists T = T(e) such that the problem (39) has a unique solution
{u{y,t),r{y.t),p{y,t)) such thatue C
2+a
{n
b
), u
t
e C{Sl
b
), r e C
1+a
{Q
b
), p 6 C
3+a
(Si)
for arbitrary t 6 (0,T), and
Y
T
(u,r,p)
= sup(|u
(
(-,t)|c«(n
b
) + |u(-,i)|
C
2+c
(«b) "
K-,*)l
ci+»(n„)
+ |P(->*)|C3+"(.9
1
))
<
C
(
T
) (|uo|c
2
+»(n
b
) + |po|c3+«(Si)) •
Proof.
We write the problem in the form

197
u
f
—
vV
2
u + Vr = f (u, r, p)
—
2cje
3
x u,
Vu = 0,
rii,S(u)n(, = Ili,b(u,p),
-r + vn
b
• S(u)n
6
-an
b
-
A
b
{p{y/\y\,t)e
T
) = d{u,p) + JF^po)
r
d_
J odt
T
x
d,T
+ Ti{p),
(48)
n;,
•
e
r
p
f
= u
•
ni, + h(u, p)
u(?/,0) = u
0
(y)
p(y,o) = po{y)
y£T
b
,t>0,
and apply the method of successive approximations. We put u'°'(y,t) = u
0
, r'
0
' =
0, p
(0)
(z/,<) = Po(y), and define (u(
m+
%,i)y
m+1
>(i/,i),p(
m
+
1
%,t)), m =
0,1,...
as a
solution to the linear problem
u,
(m+l)
•
v
V
2
u(
m+1)
+ Vr(
m+1
> = f(u(
m
>, r<
m
>, p
(m
>) - 2we
3
x u<
ro
>,
v
.
u
(m+i)
= 0)
n
6
s(u(
m+1
')n
b
=
n
6
b(u(
m
),p(
m
)),
_
r
(m+l)
+
^ . S(u<
m+1
')n
6
-an
h
-k
b
{p^+
l
Ky/\y\,t)e
T
) = d(u<™\pM) + ^i(po)
-/'J^i(p
(m)
)dT + ^
2
(p("
v. Q ^(
m
+
1
) „(m+l) „
n;,
•
e
r
p
£
—
u
v T
'
•
rij,
h(u(
m
',p(
m
>
,
>
„(-+!%, 0) = u
0
(y)
P
(m+1)
(y,0) = po(y)
By virtue of (43), for arbitrary t G (0,T) :
y^uW.r
1
',^
1
') < ci (|u
0
|
c
»+«(n
t
) + |Po|c3+«(
Sl
))
Let us estimate y
(
(
u
(
m+1
',r
m+1)
,P
(m+1)
) assuming that
yr(u
(
*V
(A0
,P
(i;)
)<<S, fc =
l,..,m.
For k = 1 this inequality holds, if Cj£ < 5. The differences
yeT
b
,t>0,
y e fifc,
2/GSi,
(49)
(50)
,(*+!)
=
„(fc+l) ,(*0
p(fc+i)
=r
(fc+i) _
r
W
£(*+!)
= p
(fc+l) _
p
<
,(*)
satisfy the relations

198
vf
+1)
- i/VM
fc+1
) + Vp(*
+1
) = f
(uO,
r«, p«) - 2ve
3
x v^
-f(
u
(fc-i)
i7
.(fc-i)
iP
(fc-i))
i
V-v(
fc+1
> = 0,
iuscv^
1
))^
=
n
6
b(u(
fc
),
P
W)-n
i
,b(u(
fc
-
1
),p(*-
1
)),
_p(*+i) + j.n,. S(v(
fc+1
))n
6
-an
b
•
A
b
(V<=+D (lL,t\ e
r
\ = d(u«,p«) - ^u^pC*"
1
))
n„
•
e
r
d
fc+1)
- v<
fc+1
)
•
n
b
= /i(u(
fc
\ p«) - fc(u
(fc
~
1)
,P
(fc
-
1)
), 2/ e r
t
, t > 0,
v
(fc+1)
(2/,0) = 0 yeQ
b
,
Z
{h+1)
(y,0) = 0 ye St.
(51)
We estimate (v*
+1
, p
k+1
, r^"
1-1
') by inequality (43) taking account of (46) and of the
elementary relation
|v«(-,*)lc«(n
t
)< f \y
{k)
(;r)\c^
b
)dr.
J 0
As a result, we arrive at
y
t
(w<*
+1
\p
t+1
\f<*
+1
>) <c
2
(T) (8
1
Y
t
(w^
k
\
P
k
\^)+ /"V
T
(wW,p
fc)
^
(fc)
)d
1
Hence
m+l
k=i
+c
2
f*xiy
t
(ww,p*)
)
e
w
)+
rx)V
T
(ww,p*),e
w
)dT
It follows that, if c
2
5 < 1/2, then, by virtue of (49) and of Gronwall's inequality
y
(
(
u
(™+V
m+1)
,P
(m+1)
) < Et^Y
t
(^
k)
,^\e
k)
)
(52)
< C{T) (|u
0
|
C
2+«(S2
t
) + |Po|c'+"(Si)) •
Hence, condition (50) is satisfied also for k = m + 1, if c(T)e < 8\. We see that the
parameters 5 and e should satisfy the condition :
max(ci,c(T))e<(5< —-. (53)
2c
2
In this case we can repeat the above argument and show that (50) holds for all k =
1,2,3, the sequences (u'
m
'
l
r'"
l
',p'
m
') are convergent in the norm Yr(->
•>
•) to the solution
of the problem (39) and the solution satisfies (52). The uniqueness of the solution also

199
follows from the inequality (43) applied
to
the difference
of
two solutions
of
the problem
(39) (we omit
the
details). Next,
we
obtain uniform estimates
for the
solution
of the
problem
(39)
defined
in an
arbitrary time interval (0,T).
To
this end,
we
evaluate
the
norm
Y
toA
u
,
r
>P)
=
SU
P
|u
s
(-,s)|c«(n
6
)+
sup
|u(-,s)|
C
2+„
(fi6
)
to — T<S<to tQ—T<S<t(j
+
sup
|r(-,s)|
c
i+«
(ni;)
+
sup
|p(-,s)|
C
3+«
(Sl)
,
(0—
T<S<*0 to — T<S<to
with
a
fixed
r €
(0,1] and with
i
0
>
2T.
Theorem
7.4 If
sup |u
s
(-,s)|
c
=(n
1
,)+
sup
|u(-,s)|c2+«(n
b
)
*0 — T<S<to to~T<S<to
(^A.}
+
sup
|r(-,s)|
c
i+«(n
t
)
sup
|p(-,s)|
C
3+«
(Sl)
<
<5,
to—r<s<to to—T<s<to
with some sufficiently small
5 > 0,
then
the
solution
of
the problem
(39)
satisfies
the
inequality
y"to,r(u,r,p)
<c( sup
||u(-,s)||
L2(
n
b
)+
sup
\\p{-,s)\\
w
i
(Sl
)
) , (55)
\t
1
<s<t
0
t
1
<s<t
0
J
where
t\ = t
0
—
2T,
T is a
small positive number and
c =
C(T)
is a
constant independent
of
t
0
.
Proof.
We
set
w
= UCA,
q =
r(
x
,
where
(,\(t)
is an
infinitely differentiable function such that
CA(*)
=
1 for£>£
1
+
2A,
CA(*)
= 0 for t < h +
A,
\('
x
{t)\
<
cA"\
and
A
€
(0, r/2). The functions
w
and
q
satisfy the relations
Vw
= 0,
w
(
-
!/V
2
w
+
Vq
= f +
u&
y e
Q
b
,
*
> h
noS(w)n
6
= bCA,
u|
t=t0
= 0.
Moreover, integrating
by
parts
in
[n
6
•
T(u,
r)n
b
- an
b
•
A
b
e
r
p\(
x
-
[n
b
•
T(u,r)n
b
- an
•
A
b
e
r
p]C
x
{t')dt'
J ti
=
{d +
F)Cx{t)-
f
(d
+ f)(
x
(t')dt',
J t-l
(56)
