Барков Ю.А., Зверев О.М., Перминов А.В. Сборник задач по общей физике
Подождите немного. Документ загружается.

231
щая на него, равна 1,5 · 10
–3
Н. Напишите уравнение движения этого
тела, если период колебания равен 2 с и начальная фаза π/3.
6.
Диск радиусом 24 см колеблется около горизонтальной
оси, проходящей через край диска перпендикулярно к плоско-
сти диска. Определите период Т колебаний такого физического
маятника.
7.
Точка участвует в двух одинаково направленных колебаниях:
х
1
= А
1
· sin ωt и х
2
= А
2
· соs ωt, где А
1
= 3 см, А
2
= 4 см, ω = 1 рад/с. Оп-
ределите амплитуду результирующих колебаний и их частоту.
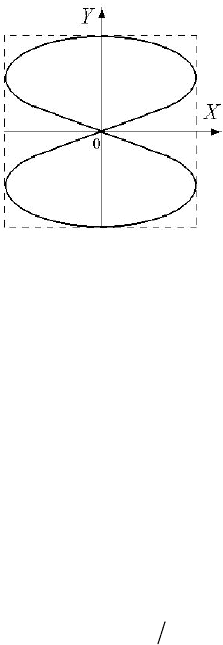
8.
Точка одновременно участвует
в двух взаимно перпендикулярных гармо-
нических колебаниях с циклическими
частотами ω
X
и ω
Y:
11
cos(ωφ
)
X
xA t=+
и
22
cos(ωφ
)
Y
yA t=+
. Траектория точки
представлена на рисунке (фигура Лисса-
жу). Каково отношение частот ω
Y
/ω
X
?
9.
Логарифмический декремент за-
тухания математического маятника ра-
вен 0,2. Найдите, во сколько раз уменьшится амплитуда колеба-
ний за одно полное колебание маятника.
10. 0
т источника колебаний распространяются волны вдоль
прямой линии. Амплитуда колебаний 5 см. Каково смещение точ-
ки, удаленной от источника на 3/4 длины волны в момент, когда
от начала колебаний источника прошло время, равное 0,5 перио-
да колебаний?
11.
Волны распространяются в упругой среде со скоростью
300
м/с. Наименьшее расстояние между точками среды, фазы кото-
рых противоположны, равно 1,5 м. Определите частоту колебаний.
Модуль 3. Колебания и волны
Вариант 14
1.
Уравнение колебаний имеет вид
3sin2π(16),смxt=+
.
Чему равны период, амплитуда, фаза и начальная фаза этих коле-
баний?
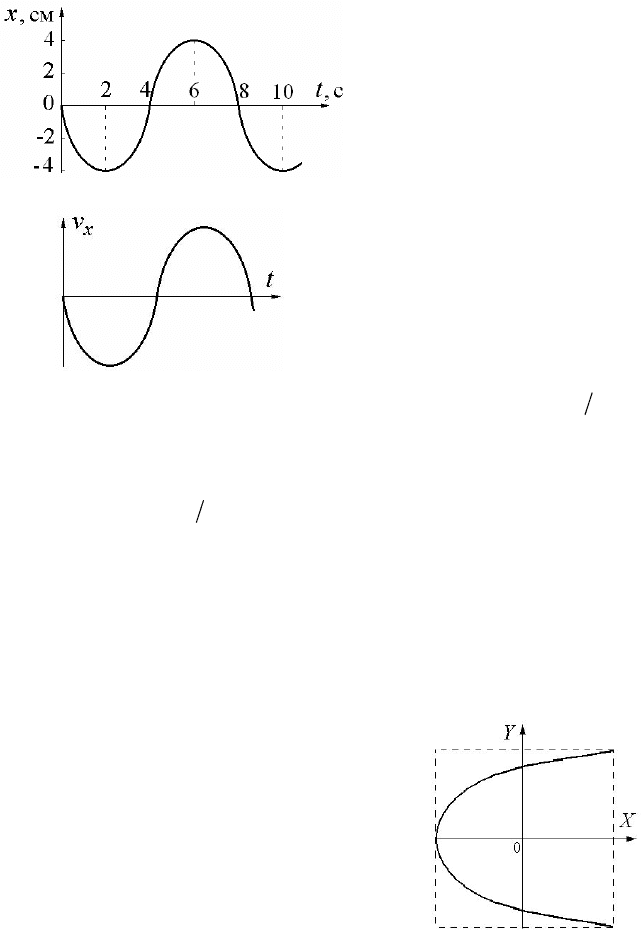
232
2. Зависимость координа-
ты колеблющегося тела от вре-
мени представлена графиком на
рисунке. Напишите в СИ урав-
нение гармонических колеба-
ний в виде
0
cos(ωφ
)
xA t=+
.
3.
Линейный гармони-
ческий осциллятор совершает
колебания. График временной
зависимости проекции его
скорости v
x
представлен на
рисунке. Нарисуйте график,
правильно отражающий за-
висимость координаты х от
времени.
4.
Уравнение движения точки дано в виде sinπ 6,смxt= .
Найдите моменты времени, в которые достигается максимальная
скорость и максимальное ускорение.
5.
Уравнение гармонического колебания тела массой 2 кг
имеет вид sinπ 6,смxt= . Определите скорость и кинетическую
энергию в момент времени t = 3 с.
6.
На сколько уменьшится число колебаний математического
маятника с периодом колебаний 1 с за сутки, если длина его возрас-
тет на 5 см?
7.
Материальная точка участвует одновременно в двух коле-
баниях, происходящих по одной прямой и выражаемых уравнения-
ми: х
1
= sin πt, м, и х
2
= 2sin(πt+π/2), м. Определите амплитуду ре-
зультирующего колебания, его частоту
и начальную фазу.
8.
Точка одновременно участвует
в двух взаимно перпендикулярных гар-
монических колебаниях с циклическими
частотами ω
X
и ω
Y:
11
cos(ωφ
)
X
xA t=+ и
22
cos(ωφ
)
Y
yA t=+
. Траектория точки пред-
ставлена на рисунке (фигура Лиссажу).
Каково отношение частот ω
Y
/ω
X
?
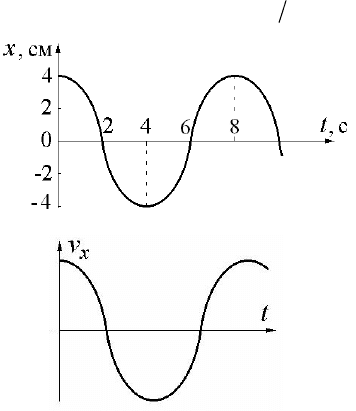
233
9. Математический маятник отклонился при первом колебании
в одну сторону на 5 см, при втором колебании на 4 см в ту же сторону.
Определите: а) декремент; б) логарифмический декремент затухания.
10.
Задано уравнение плоской волны ξ = A · cos(ωt – kλ), где
А = 0,5 см, ω = 628 рад/с, k = 2 1/м. Определите: 1) частоту коле-
баний и длину волны; 2) максимальное значение скорости коле-
баний частиц среды.
11.
Определите разность фаз ∆ϕ колебаний источника волн,
находящегося в упругой среде, и точки этой среды, отстоящей на
0,3
м от источника. Частота колебаний равна 100 Гц; волны распро-
страняются со скоростью 330 м/с.
Модуль 3. Колебания и волны
Вариант 15
1.
Определите амплитуду, период, циклическую частоту и на-
чальную фазу колебаний, заданных уравнением
5cos2π(18),смxt=+
.
2.
Зависимость коор-
динаты колеблющегося тела
от времени представлена
графиком на рисунке. На-
пишите в СИ уравнение
гармонических колебаний
в виде
0
cos(ωφ
)
xA t=+
.
3.
Линейный гармони-
ческий осциллятор совершает
колебания. График времен-
ной зависимости проекции
его скорости v
x
представлен
на рисунке. Нарисуйте гра-
фик, правильно отражающий
зависимость координаты х от
времени.
4.
Уравнение гармонического колебания тела имеет вид
5sin
π(0,5),смxt=+. Определите скорость в момент времени 6 с
и максимальное ускорение.
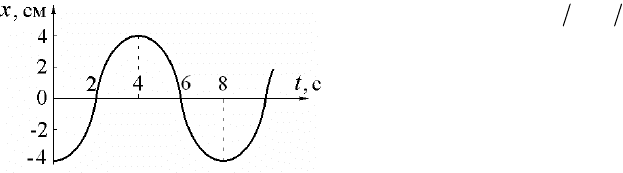
234
5. Материальная точка массой 10 г совершает колебания со-
гласно уравнению
5sinπ(0,4),смxt=+
. Найдите силу, действую-
щую в момент времени t = 0,1 с, а также полную энергию точки.
6.
Как относятся частоты колебаний математических маятни-
ков, если длины относятся как 1:9?
7.
Два одинаково направленных колебания складываются
в одно. Напишите уравнение результирующего колебания, если скла-
дываемые колебания заданы уравнениями: x
1
= 3sinωt, x
2
= 4cosωt.
8.
Точка совершает одновременно два гармонических колеба-
ния, происходящих во взаимно перпендикулярных направлениях и
выражаемых уравнениями: х = 4cosπt и у = 3sinπt (длина в см, время
в секундах). Определите уравнение траектории точки, постройте ее
с соблюдением масштаба и укажите направление движения.
9.
Амплитуда 3-го колебания больше амплитуды 11-го коле-
бания в 32 раза. Во сколько раз амплитуда затухающих колебаний
уменьшится за одно полное колебание?
10.
Поперечная волна распространяется вдоль оси Х. Уравне-
ние незатухающих колебаний источника дано в виде у = 10sin 0,5πt,
см. Найдите смещение от положения равновесия точки, находящей-
ся на расстоянии 75 см от источника колебаний через 2 с после на-
чала колебаний. Скорость распространения колебаний 3 м/с.
11.
Найдите разность фаз колебаний двух точек, находящихся на
расстояниях соответственно 4 и 10 м от источника колебаний. Частота
колебаний 25 Гц, скорость распространения колебаний 300 м/с.
Модуль 3. Колебания и волны
Вариант 16
1.
Уравнение колебаний
имеет вид
4,2sin(π 2 π 8
),
xt=+
см. Чему равны период, ампли-
туда, фаза и начальная фаза этих
колебаний?
2.
Зависимость координа-
ты колеблющегося тела от вре-
мени представлена графиком
235
на рисунке. Напишите в СИ уравнение гармонических колебаний
в виде
0
cos(ωφ
)
xA t=+.
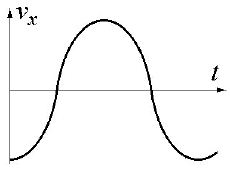
3.
Линейный гармонический осцил-
лятор совершает колебания. График вре-
менной зависимости проекции его скоро-
сти v
x
представлен на рисунке. Нарисуйте
график, правильно отражающий зависи-
мость координаты х от времени.
4.
Точка совершает гармонические
колебания. Максимальная скорость точки равна 10 см/с, макси-
мальное ускорение 100 см/с
2
. Найдите циклическую частоту коле-
баний, их период и амплитуду. Напишите уравнение.
5.
Тело массой 5 г совершает колебания с частотой 2 Гц. Ам-
плитуда колебаний 3 мм. Определите: 1) максимальную силу, дей-
ствующую на точку; 2) полную энергию колеблющейся точки.
6.
Диск радиусом 75 см колеблется около горизонтальной оси,
проходящей на расстоянии 50 см от оси диска перпендикулярно
к плоскости диска. Определите частоту ν колебаний такого физиче-
ского маятника.
7.
Два одинаково направленных гармонических колебания
одинаковой частоты с амплитудами 28 и 45 мм складываются в од-
но колебание с амплитудой 53 мм. Какова разность фаз складывае-
мых колебаний?
8.
Материальная точка одновременно участвует в двух взаим-
но перпендикулярных колебаниях одинаковой частоты, заданных
уравнениями: х = 4sin(ω
0
t + π/2), см, и у = 3sin(ω
0
t), см. Найдите
уравнение траектории, постройте ее с соблюдением масштаба
и укажите направление движения.
9.
Чему равен логарифмический декремент затухания матема-
тического маятника, если за 1 мин амплитуда колебаний уменьши-
лась в 2 раза? Длина маятника 9,81 м.
10.
Найдите смещение от положения равновесия точки, от-
стоящей от источника колебаний на расстоянии L = λ/6 (λ – длина
волны) для момента времени Т/3 (Т – период колебаний). Амплиту-
да колебаний А = 0,05 м.
11.
Определите скорость распространения волн в упругой
среде, если разность фаз колебаний двух точек среды, отстоящих
друг от друга на 10 см, равна π/6, а частота колебаний 500 Гц.
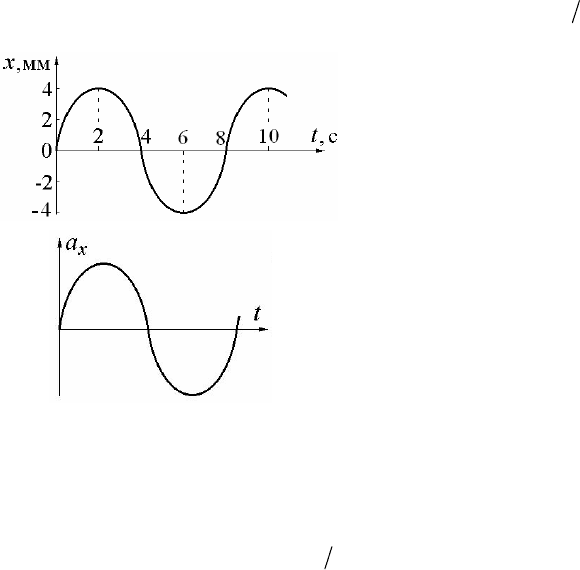
236
Модуль 3. Колебания и волны
Вариант 17
1.
Определите амплитуду, период, циклическую частоту и на-
чальную фазу колебаний, заданных уравнением
3sin2π(14),смxt=+
.
2. Зависимость координа-
ты колеблющегося тела от вре-
мени представлена графиком на
рисунке. Напишите в СИ урав-
нение гармонических колеба-
ний в виде
0
sin(ωφ
)
xA t=+
.
3.
Линейный гармони-
ческий осциллятор совершает
колебания. График временной
зависимости проекции его
ускорения а
x
представлен на
рисунке. Нарисуйте график,
правильно отражающий зави-
симость координаты х от вре-
мени.
4.
Напишите уравнение гармонического колебательного дви-
жения, если максимальное ускорение точки 49,3 см/с
2
, частота ко-
лебаний 0,4 Гц и смещение точки от положения равновесия в на-
чальный момент времени 25 мм.
5.
Материальная точка массой 10 г совершает колебания со-
гласно уравнению
3sin2π(14),смxt=+
. Найдите силу, действую-
щую в момент времени t = 0,25 c, а также полную энергию точки.
6.
Обруч диаметром 113 см висит на гвозде, вбитом в стену,
и совершает малые колебания в плоскости, параллельной стене.
Найдите период этих колебаний.
7.
Два одинаково направленных колебания складываются в од-
но. Напишите уравнение результирующего колебания, если склады-
ваемые колебания заданы уравнениями: x
1
= 12sin ωt, x
2
= 5cos ωt.
8.
Материальная точка одновременно участвует в двух взаим-
но перпендикулярных колебаниях одинаковой частоты, заданных
уравнениями: х = 2sin ωt, см, и у = 3sin(ωt + π), см. Найдите уравне-
237
ние траектории, постройте ее с соблюдением масштаба и укажите
направление движения.
9.
Задано уравнение колебаний
0,01
π
5sin(2π
)
2
t
xe t
−
=+
, см.
Найдите коэффициент затухания и время релаксации.
10.
Волны с периодом 0,6 с и амплитудой 5 см распространя-
ются со скоростью 20 м/с. Чему равно смещение точки, находящей-
ся на расстоянии 40 м от источника волн в тот момент, когда от на-
чала колебаний прошло 2 с?
11.
Две точки находятся на прямой, вдоль которой распро-
страняются волны со скоростью 400 м/с. Частота колебаний 100 Гц,
расстояние между точками 40 см. Найдите разность фаз колебаний
этих точек.
Модуль 3. Колебания и волны
Вариант 18
1.
Определите амплитуду, период, циклическую частоту и на-
чальную фазу колебаний, заданных уравнением
6sinπ(14),смxt=+
.
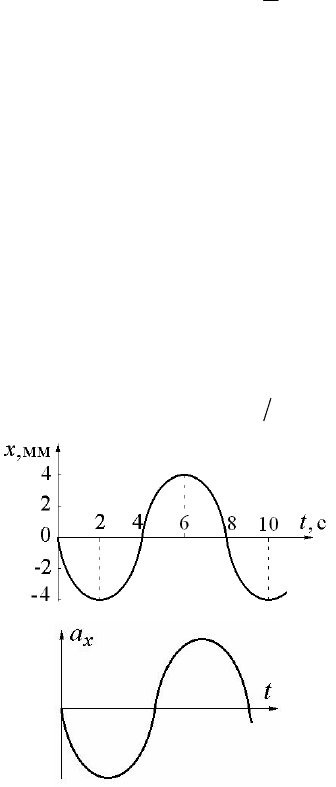
2.
Зависимость координа-
ты колеблющегося тела от вре-
мени представлена графиком на
рисунке. Напишите в СИ урав-
нение гармонических колеба-
ний в виде
0
sin(ωφ
)
xA t=+.
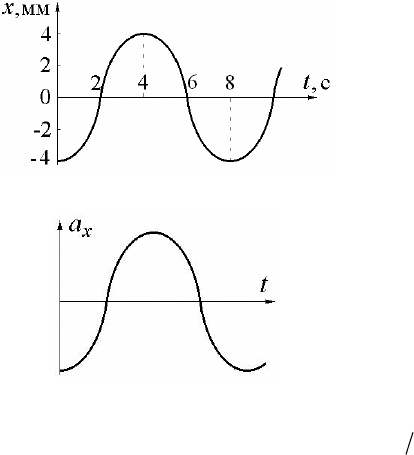
3.
Линейный гармони-
ческий осциллятор совершает
колебания. График времен-
ной зависимости проекции
его ускорения а
x
представлен
на рисунке. Нарисуйте гра-
фик, правильно отражающий
зависимость координаты х от
времени.
4.
Амплитуда гармонического колебания 5 см, период 4 с
и начальная фаза π/4. Напишите уравнение этого колебания. Найди-

238
те смещение, скорость и ускорение колеблющейся точки в момент
времени t = 1,5 с.
5.
Материальная точка массой 10 г совершает колебания со-
гласно уравнению
6sinπ(14),смxt=+
. Найдите силу, действую-
щую в момент времени 1,25 с, а также полную энергию точки.
6.
Из однородного диска радиусом 2R/3 сделали физический
маятник. Вначале ось проходит через образующую диска, потом на
расстоянии R/3 от центра диска. Определите отношение периодов
колебаний диска.
7.
Два одинаково направленных гармонических колебания
одинаковой частоты с амплитудами 12 и 5 мм складываются в одно
колебание с амплитудой 13 мм. Какова разность фаз складываемых
колебаний?
8.
Материальная точка участвует в двух взаимно перпенди-
кулярных колебаниях, заданных уравнениями х = cos(πt + π), см,
и y = 2cos πt, см. Найдите уравнение траектории и начертите ее
с соблюдением масштаба.
9.
Амплитуда 3-го колебания больше амплитуды 7-го колеба-
ния в 4 раза. Чему равен логарифмический декремент затухания?
10.
Источник, расположенный в точке x = 0, колеблется по
закону y = 0,02sin100πt, м. Напишите уравнение плоской бегущей
незатухающей волны, распространяющейся вдоль направления x
со скоростью 300 м/с.
11.
Найдите разность фаз колебаний двух точек, отстоящих на
расстоянии 3 м друг от друга, если длина волны равна 2 м.
Модуль 3. Колебания и волны
Вариант 19
1.
Определите амплиту-
ду, период, циклическую час-
тоту и начальную фазу коле-
баний, заданных уравнением
10cosπ(58),смxt=+
.
2.
Зависимость коорди-
наты колеблющегося тела от
времени представлена гра-
239
фиком на рисунке. Напишите в СИ урав-
нение гармонических колебаний в виде
0
sin(ωφ
)
xA t=+
.
3.
Линейный гармонический осцил-
лятор совершает колебания. График вре-
менной зависимости проекции его ускоре-
ния а
x
представлен на рисунке. Нарисуйте график, правильно отра-
жающий зависимость координаты х от времени.
4.
Амплитуда гармонического колебания 10 мм, период 2 с,
начальная фаза π/2. Напишите уравнение этого колебания. Найдите
смещение, скорость и ускорение колеблющейся точки в момент
времени t = 1,5 с.
5.
Полная энергия колеблющегося тела равна 6 · 10
–5
Дж, мак-
симальная сила, действующая на него, равна 3 · 10
–3
Н. Напишите
уравнение движения тела, если период колебания равен 1 с и на-
чальная фаза π/6.
6.
Диск радиусом 48 см колеблется около горизонтальной оси,
проходящей через образующую диска перпендикулярно к плоскости
диска. Определите частоту колебаний такого физического маятника.
7.
Складываются два гармонических колебания одного направ-
ления с одинаковыми периодами Т = 1,5 с и амплитудами А
1
= 2 см,
А
2
= 3 см. Начальные фазы колебаний ϕ
1
= π/2 и ϕ
2
= π/3. Определите
амплитуду и начальную фазу результирующего колебания. Напиши-
те его уравнение.
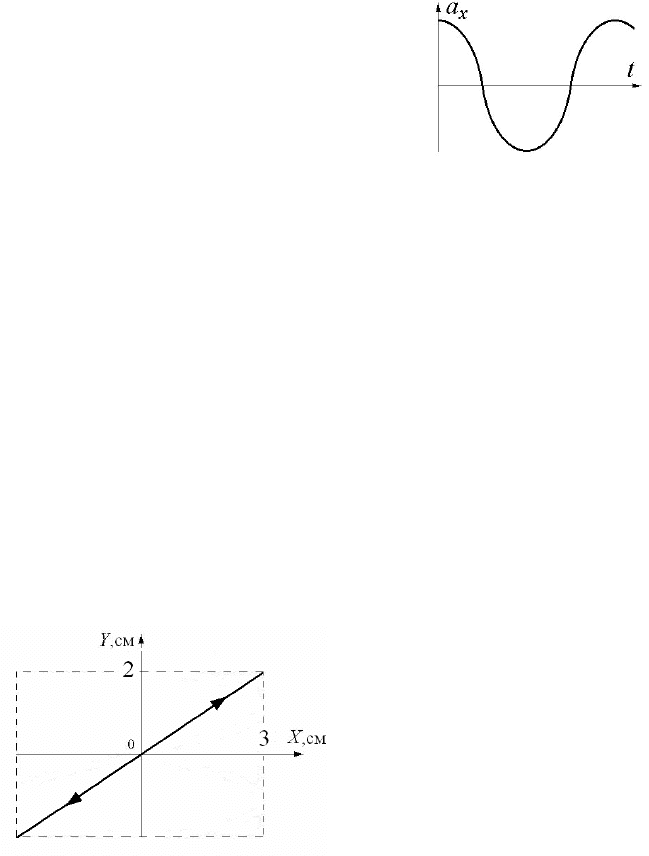
8.
Точка одновременно
участвует в двух взаимно
перпендикулярных гармони-
ческих колебаниях с цикли-
ческими частотами ω
X
= 2π,
рад/с, и ω
Y.
Траектория точки
представлена на рисунке.
Определите амплитуды, на-
чальные фазы, частоты и на-
пишите законы изменения
координат:
11
sin(ωφ
)
X
xA t=+
и
22
sin(ωφ
)
Y
yA t=+.
9.
За 8 мин амплитуда затухающих колебаний маятника
уменьшается в 3 раза. Во сколько раз амплитуда уменьшится за
4
мин, чему равен коэффициент затухания?
240
10. Поперечная волна распространяется вдоль оси Х. Уравне-
ние колебаний источника дано в виде у = 10sin 300πt, см. Найдите
смещение от положения равновесия точки, находящейся на рас-
стоянии 100 см от источника колебаний через 0,01 с после начала
колебаний. Скорость волн 300 м/с.
11.
Определите разность фаз колебаний источника волн, на-
ходящегося в упругой среде, и точки этой среды, отстоящей на 2 м
от источника. Частота колебаний равна 500 Гц; волны распростра-
няются со скоростью 400 м/с.
Модуль 3. Колебания и волны
Вариант 20
1.
Уравнение гармонических колебаний имеет вид х =
5sinπ(0,1),смt=+
. Чему равны период и циклическая частота
этих колебаний?
2.
Зависимость коор-
динаты колеблющегося тела
от времени представлена
графиком на рисунке. Напи-
шите в СИ уравнение гармо-
нических колебаний в виде
0
sin(ωφ
)
xA t=+.
3.
Линейный гармони-
ческий осциллятор совершает
колебания. График времен-
ной зависимости проекции
его ускорения а
x
представлен
на рисунке. Нарисуйте гра-
фик, правильно отражающий
зависимость координаты х от
времени.
4.
Материальная точка совершает гармонические колебания,
уравнение которых имеет вид
20sinπ 6,ммxt=
. Каково значение
скорости точки в момент времени 2 с?
