Барков Ю.А., Зверев О.М., Перминов А.В. Сборник задач по общей физике
Подождите немного. Документ загружается.

221
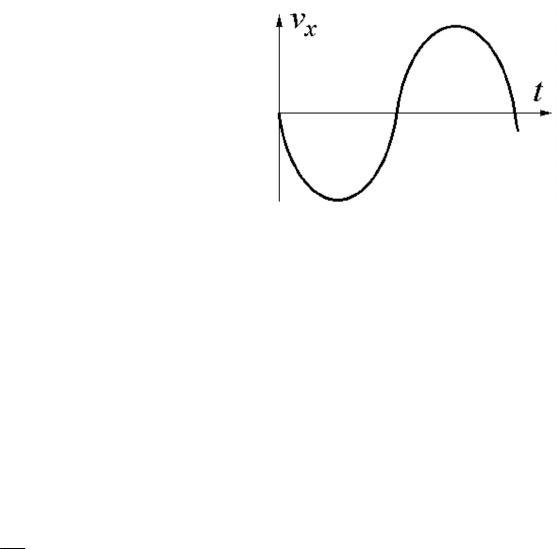
3. Линейный гармонический
осциллятор совершает колебания.
График временной зависимости про-
екции его скорости v
x
представлен на
рисунке. Нарисуйте график, пра-
вильно отражающий зависимость
проекции ускорения a
x
от времени.
4.
Частота колебаний ножки
камертона 500 Гц, амплитуда ко-
лебаний 0,1 мм. Определите максимальное ускорение.
5.
Уравнение колебания тела массой 2 кг имеет вид
5sin
π(0,5),смxt=+. Определите кинетическую энергию в момент
времени t = 6 с.
6.
Диск радиусом 24 см колеблется около горизонтальной оси,
проходящей через середину одного из радиусов перпендикулярно к.
плоскости диска. Определите частоту ν колебаний такого физическо-
го маятника.
7.
Складываются два гармонических колебания одного на-
правления с одинаковыми периодами и равными амплитудами
0
.
A
Чему равна амплитуда результирующего колебания при разности
фаз
3π
φ
2
∆= ?
8.
Точка совершает одновременно два гармонических колеба-
ния, происходящих во взаимно перпендикулярных направлениях
и выражаемых уравнениями: х = sin t/2 см и у = соs t см (время в се-
кундах). Определите уравнение траектории точки, постройте ее
с соблюдением масштаба и укажите направление движения.
9.
Период затухающих колебаний 4 с, логарифмический дек-
ремент затухания 1,6, начальная фаза равна нулю. Смещение точки
при t = Т/4 равно 4,5 см. Напишите уравнение движения этого коле-
бания и постройте его график в пределах двух периодов.
10.
Поперечная волна распространяется вдоль оси Х. Уравне-
ние незатухающих колебаний источника дано в виде у = 5sin10πt, см.
Напишите уравнение, колебаний для точки, отстоящей на расстоянии
600
м от источника колебаний, если скорость волны 300 м/с.
11.
Найдите разность фаз колебаний двух точек, отстоящих на
расстоянии 2 м друг от друга, если длина волны равна 1 м.
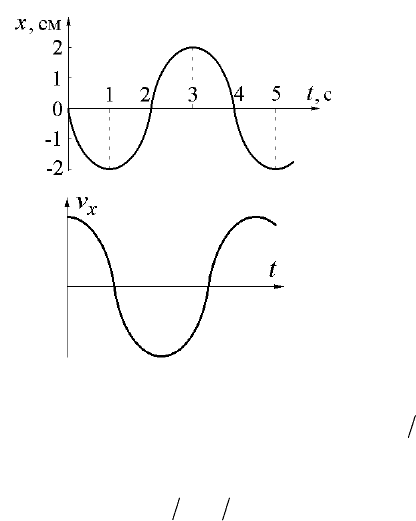
222
Модуль 3. Колебания и волны
Вариант 7
1.
Уравнение гармонических колебаний имеет вид
cos5
π , смxt= . Определите амплитуду, циклическую частоту, пе-
риод и начальную фазу этих колебаний.
2.
Зависимость координа-
ты колеблющегося тела от вре-
мени представлена графиком на
рисунке. Напишите в СИ урав-
нение гармонических колеба-
ний в виде
0
cos(ωφ
)
xA t=+
.
3.
Линейный гармониче-
ский осциллятор совершает
колебания. График временной
зависимости проекции его ско-
рости v
x
представлен на рисун-
ке. Нарисуйте график, пра-
вильно отражающий зависи-
мость проекции ускорения a
x
от времени.
4.
Материальная точка совершает гармонические колебания,
уравнение которых имеет вид 20cosπ
6
x
t= , мм. Каково значение
ускорения точки в момент времени t = 3 с?
5.
Материальная точка массой 20 г колеблется согласно урав-
нению
5cos(π 5 π 4), смxt=+
. Найдите частоту колебаний, макси-
мальную силу, действующую на точку, и ее полную энергию.
6.
Один маятник совершает в минуту 40, а другой – 60 кача-
ний. Как относятся длины этих маятников?
7.
Точка участвует в двух одинаково направленных колебани-
ях одного периода с одинаковыми начальными фазами, амплитуды
колебаний А
1
= 3 см и А
2
= 4 см. Найдите амплитуду результирую-
щего колебания.
8.
Материальная точка одновременно участвует в двух взаим-
но перпендикулярных колебаниях одинаковой частоты, заданных
уравнениями: х = 3sin ω
0
· t, см, и у = 3sin(ω
0
· t + π/2), см. Найдите
223
уравнение траектории, постройте ее с соблюдением масштаба и ука-
жите направление движения.
9.
За 600 с амплитуда затухающих колебаний маятника умень-
шилась в 3 раза. Определите коэффициент затухания.
10.
От источника колебаний распространяются волны вдоль
прямой линии. Амплитуда колебаний 10 см. Каково смещение
точки, удаленной от источника на 3/4 длины волны в момент, ко-
гда от начала колебаний источника прошло время, равное 0,9 пе-
риода колебаний?
11.
Волны распространяются в упругой среде со скоростью
75
м/с. Наименьшее расстояние между точками среды, фазы ко-
лебаний которых противоположны, равно 2 м. Определите пери-
од колебаний.
Модуль 3. Колебания и волны
Вариант 8
1.
Уравнение гармонических. колебаний тела имеет вид
4sinπ(0,1),смxt=+
. Определите амплитуду, циклическую частоту,
период и начальную фазу.
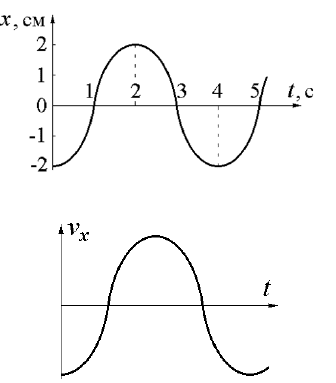
2.
Зависимость координа-
ты колеблющегося тела от вре-
мени представлена графиком на
рисунке. Напишите в СИ урав-
нение гармонических колебаний
в виде
0
cos(ωφ
)
xA t=+
.
3.
Линейный гармониче-
ский осциллятор совершает ко-
лебания. График временной за-
висимости проекции его скоро-
сти v
x
представлен на рисунке.
Нарисуйте график, правильно
отражающий зависимость про-
екции ускорения a
x
от времени.
4.
Уравнение гармониче-
ских колебаний тела имеет вид
0,2sin5π ,см
xt
= . Каково макси-
мальное ускорение этого тела?
224
5. Материальная точка массой 20 г совершает колебания со-
гласно уравнению 0,1sin4π ,м
xt
= . Найдите силу, действующую
в момент времени t = 0,2 с, а также полную энергию точки.
6.
Тонкий обруч, повешенный на гвоздь, вбитый горизонталь-
но в стену, колеблется в плоскости, параллельной стене. Радиус об-
руча 30 см. Вычислить период Т его колебаний.
7.
Напишите уравнение движения, получающегося от сложе-
ния двух одинаково направленных гармонических колебаний с оди-
наковыми периодами по 8 с и одинаковыми амплитудами по 2 см.
Начальная фаза одного колебания равна нулю, второго – π/4.
8.
Материальная точка одновременно участвует в двух взаим-
но перпендикулярных колебаниях одинаковой частоты, заданных
уравнениями: х = 2sin ωt, см, и у = 3sin(ωt + π/2), см. Найдите урав-
нение траектории, постройте ее с соблюдением масштаба и укажите
направление движения.
9.
Амплитуда затухающих колебаний маятника за 1 мин умень-
шилась вдвое. Во сколько раз она уменьшится за 4 мин?
10.
Волны с периодом 1,2 с и амплитудой 3 см распространя-
ются со скоростью 15 м/с. Чему равно смещение точки, находящей-
ся на расстоянии 30 м от источника волн в тот момент, когда от на-
чала колебаний прошло 3 с?
11.
Найдите разность фаз колебаний двух точек, отстоящих на
расстоянии 4 м друг от друга, если длина волны равна 3 м.
Модуль 3. Колебания и волны
Вариант 9
1.
Определите амплитуду, период, циклическую частоту
и начальную фазу колебаний, заданных уравнением х =
5cos10π(0,1),смt=+
.
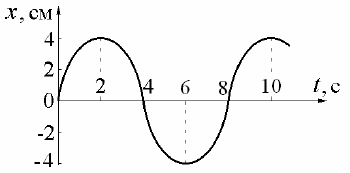
2.
Зависимость коор-
динаты колеблющегося тела
от времени представлена
графиком на рисунке. Напи-
шите в СИ уравнение гармо-
нических колебаний в виде
0
sin(ωφ
)
xA t=+
.
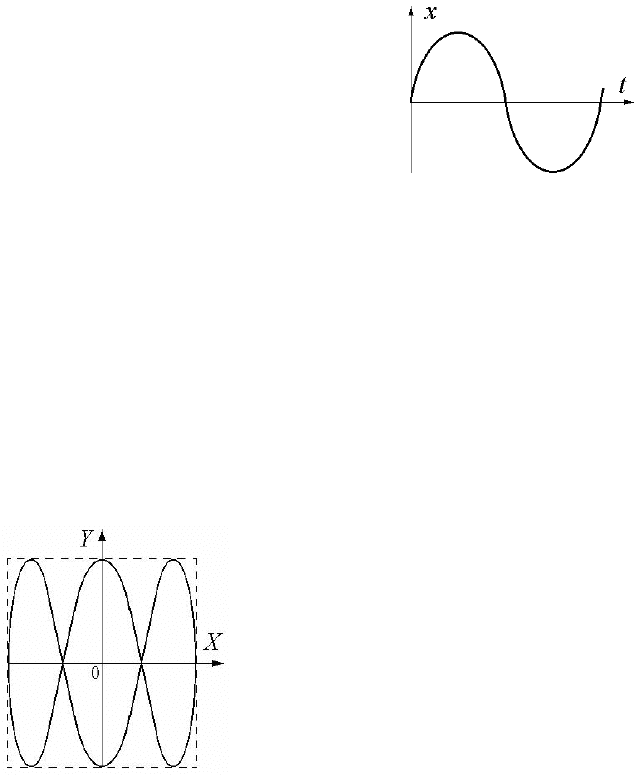
225
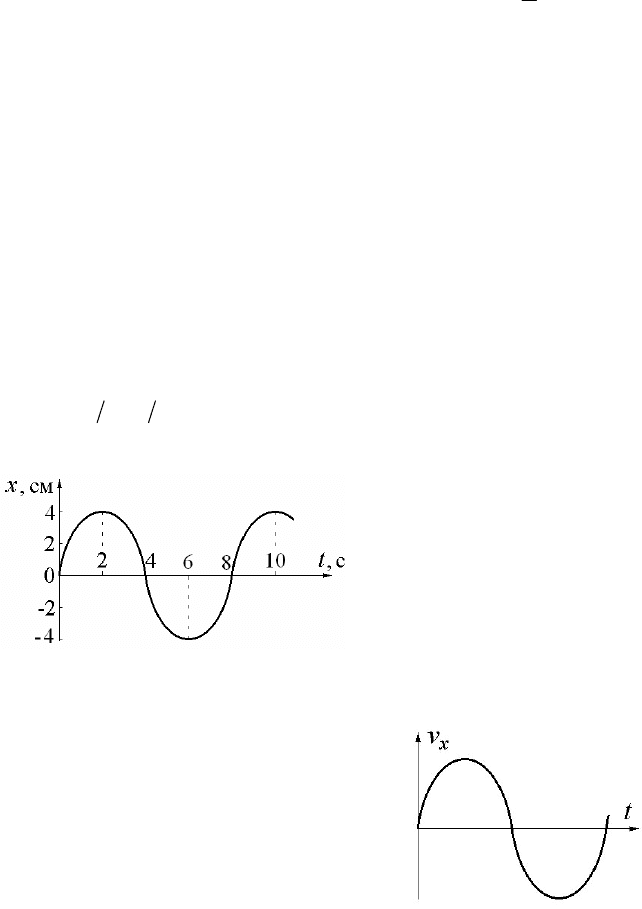
3. Линейный гармонический осцил-
лятор совершает колебания. График вре-
менной зависимости его координаты х
представлен на рисунке. Нарисуйте гра-
фик, правильно отражающий зависимость
проекции ускорения a
x
от времени.
4.
Напишите уравнение гармони-
ческого колебательного движения, если
максимальное ускорение точки 98,6 см/с
2
, период колебаний 2 с
и смещение точки от положения равновесия в начальный момент
времени 25 мм.
5.
Уравнение колебания тела массой 2 кг имеет вид х =
5cosπ(0,1),смt=+
. Определите потенциальную энергию в момент
времени t = 5 с.
6.
Маятник длиной 2 м совершает 1268 колебаний в час. Най-
дите ускорение силы тяжести.
7.
При сложении двух гармонических колебаний одного на-
правления с одинаковыми периодами и равными амплитудами ре-
зультирующее колебание имеет такую же амплитуду, что и склады-
ваемые колебания. Чему равна разность фаз исходных колебаний?
8.
Точка одновременно участвует
в двух взаимно перпендикулярных гар-
монических колебаниях с циклическими
частотами ω
X
и ω
Y:
11
cos(ωφ
)
X
xA t=+
и
22
cos(ωφ
)
Y
yA t=+
. Траектория точки
представлена на рисунке (фигура Лисса-
жу). Каково отношение частот ω
Y
/ω
X
?
9.
Амплитуда колебаний маятни-
ка длиной 2 м за 2 мин уменьшилась
в 2 раза. Определите логарифмический
декремент затухания.
10.
Поперечная волна распространяется вдоль оси Х. Уравне-
ние незатухающих колебаний источника дано в виде у = 5sin 100πt,
см. Напишите уравнение волны, если скорость распространения
колебаний 100 м/с.
11.
Определите разность фаз ∆ϕ колебаний источника волн,
находящегося в упругой среде, и точки этой среды, отстоящей на
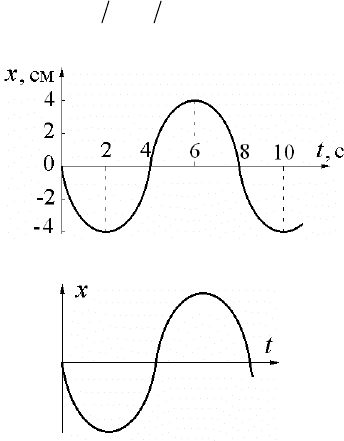
226
2 м от источника. Частота колебаний равна 5 Гц, волны распростра-
няются со скоростью 40 м/с.
Модуль 3. Колебания и волны
Вариант 10
1.
Материальная точка совершает колебания по закону
2sin(π 4 π 2
)
xt=+
, где х – в см, t – в секундах. Определите ампли-
туду колебаний, начальную фазу и период.
2.
Зависимость коор-
динаты колеблющегося тела
от времени представлена
графиком на рисунке. На-
пишите в СИ уравнение
гармонических колебаний
в виде
0
sin(ωφ
)
xA t=+
.
3.
Линейный гармони-
ческий осциллятор соверша-
ет колебания. График вре-
менной зависимости его ко-
ординаты х представлен на
рисунке. Нарисуйте график,
правильно отражающий за-
висимость проекции ускоре-
ния a
x
от времени.
4.
Уравнение гармонического колебания тела имеет вид
5sin
π(0,5),смxt=+. Определите максимальную скорость и ус-
корение в момент времени 6 с.
5.
Амплитуда гармонических колебаний материальной точки
А = 2 мм, полная энергия колебаний W = 2 · 10
–7
Дж. При каком сме-
щении от положения равновесия на колеблющуюся точку действует
сила 10
–6
Н?
6.
Однородный стержень длиной 0,5 м совершает малые коле-
бания в вертикальной плоскости около горизонтальной оси, прохо-
дящей на расстоянии 10 см от его верхнего конца. Определите пе-
риод колебаний стержня.
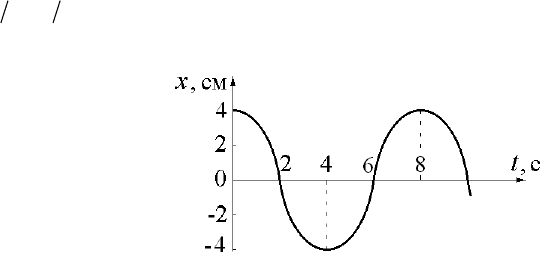
227
7. Материальная точка участвует одновременно в двух коле-
баниях, происходящих по одной прямой и выражаемых уравнения-
ми: х
1
= sinπ(t + 1/6), см, и х
2
= 2sinπ(t+1/6), см. Определите ампли-
туду результирующего колебания.
8.
Материальная точка одновременно участвует в двух взаим-
но перпендикулярных колебаниях одинаковой частоты, заданных
уравнениями: х = 2sin ω
0
t, см, и у = 3sin(ω
0
t+π), см. Найдите уравне-
ние траектории, постройте ее с соблюдением масштаба и укажите
направление движения.
9.
Логарифмический декремент затухания колебаний маятни-
ка равен 0,003. Сколько полных колебаний должен сделать маятник,
чтобы амплитуда уменьшилась в два раза?
10.
Поперечная волна распространяется вдоль упругого шну-
ра со скоростью 15 м/с. Период колебаний точек шнура Т = 1,2 с,
амплитуда 2 см. Определите: 1) фазу колебаний; 2) смещение точки,
отстоящей на расстояний 45 м от источника волн в момент времени
t = 4
с.
11.
Определите разность фаз колебаний источника волн, на-
ходящегося в упругой среде, и точки этой среды, отстоящей на 2 м
от источника. Частота колебаний равна 20 Гц, волны распространя-
ются со скоростью 100 м/с.
Модуль 3. Колебания и волны
Вариант 11
1.
Материальная точка совершает колебания по закону
2sin(π 4 π 2
)
xt=+
, где х – в см, t – в секундах. Определите ам-
плитуду колебаний, начальную фазу и период.
2.
Зависимость ко-
ординаты колеблющего-
ся тела от времени пред-
ставлена графиком на
рисунке. Напишите в СИ
уравнение гармониче-
ских колебаний в виде
0
sin(ωφ
)
xA t=+
.
228
3. Линейный гармонический ос-
циллятор совершает колебания. График
временной зависимости его координаты х
представлен на рисунке. Нарисуйте гра-
фик, правильно отражающий зависи-
мость проекции ускорения a
x
от времени.
4.
Амплитуда гармонических коле-
баний 5 мм, период 0,4 с. Найдите максимальную скорость колеб-
лющейся точки и ее максимальное ускорение.
5.
Материальная точка массой 10 г колеблется с периодом
0,25
с и амплитудой 2 см. Определите полную энергию колеблю-
щейся точки.
6.
Найдите приведенную длину физического маятника, часто-
та колебаний которого равна 0,5 Гц.
7.
Найдите амплитуду и начальную фазу гармонического
колебания, полученного от сложения одинаково направленных
колебаний, заданных уравнениями: х
1
= 0,02sin(5πt + π/2), м,
и х
2
= 0,03sin(5πt + π/4), м.
8.
Точка участвует одновременно в двух взаимно перпенди-
кулярных колебаниях: х = 2sin ωt и у = 2cos ωt. Найдите траекторию
движения точки.
9.
Амплитуда затухающих колебаний маятника за 1 мин
уменьшилась вдвое. Во сколько раз она уменьшится за 4 мин?
10.
Источник, расположенный в точке х = 0, колеблется по
закону, у = Аcosωt. Напишите уравнение плоской бегущей неза-
тухающей волны, распространяющейся вдоль направления х со
скоростью v.
11.
Найдите разность фаз колебаний двух точек, находящихся на
расстояниях соответственно 10 и 16 м от источника колебаний. Период
колебаний 0,04 с, скорость распространения колебаний 300 м/с.
Модуль 3. Колебания и волны
Вариант 12
1.
Уравнение гармонических колебаний имеет вид х =
5sin
π(0,1),смt=+. Чему равны период и циклическая частота
этих колебаний?

229
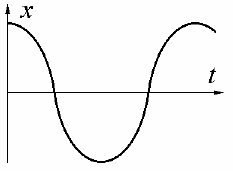
2. Зависимость координа-
ты колеблющегося тела от вре-
мени представлена графиком на
рисунке. Напишите в СИ урав-
нение гармонических колебаний
в виде
0
sin(ωφ
)
xA t=+
.
3.
Линейный гармониче-
ский осциллятор совершает ко-
лебания. График временной
зависимости его координаты х
представлен на рисунке. Нари-
суйте график, правильно отра-
жающий зависимость проекции
ускорения a
x
от времени.
4.
Напишите уравнение гармонического колебательного дви-
жения, если максимальная скорость точки 31,4 см/с, период колеба-
ний 2 с и смещение точки от положения равновесия в начальный
момент времени равно 25 мм.
5.
Материальная точка массой 10 г совершает колебания со-
гласно уравнению 5sinπ(0,1),смxt=+. Найдите силу, действую-
щую в момент времени t = 0,4 с, а также полную энергию точки.
6.
Диск радиусом 24 см колеблется около горизонтальной оси,
проходящей через середину одного из радиусов перпендикулярно
к плоскости диска. Определите период Т колебаний такого физиче-
ского маятника.
7.
Складываются два гармонических колебания одного на-
правления с одинаковыми частотами и равными амплитудами
0
A
.
Чему равна амплитуда результирующего
колебания при разности фаз φπ∆=.
8.
Точка одновременно участвует
в двух взаимно перпендикулярных гар-
монических колебаниях с циклическими
частотами ω
X
и ω
Y:
11
cos(ωφ
)
X
xA t=+
и
22
cos(ωφ
)
Y
yA t=+
. Траектория точки
представлена на рисунке (фигура Лисса-
жу). Каково отношение частот ω
Y
/ω
X
?
230
9. Задано уравнение колебаний
0,1
π
8sin(π
)
4
t
xe t
−
=+
, см. Най-
дите коэффициент затухания и время релаксации.
10.
Поперечная волна распространяется вдоль оси Х. Уравне-
ние колебаний источника дано в виде у = 4sin 600πt, см. Найдите
смещение от положения равновесия точки, находящейся на рас-
стоянии 75 см от источника колебаний через 0,01 с после начала
колебаний. Скорость волны 300 м/с.
11.
Определите скорость распространения волн в упругой
среде, если разность фаз колебаний двух точек среды, отстоящих
друг от друга на 20 см, равна π/4, а частота колебаний 50 Гц.
Модуль 3. Колебания и волны
Вариант 13
1.
Материальная точка совершает колебания по закону
2sin(π 6 π 3), смxt=+
. Определите амплитуду колебаний, началь-
ную фазу и период.
2.
Зависимость коор-
динаты колеблющегося тела
от времени представлена
графиком на рисунке. Напи-
шите в СИ уравнение гармо-
нических колебаний в виде
0
cos(ωφ
).
xA t=+
3.
Линейный гармони-
ческий осциллятор совершает колебания. График временной зави-
симости проекции его скорости v
x
представлен на рисунке. Нари-
суйте график, правильно отражающий
зависимость координаты х от времени.
4.
Частота колебаний ножки камер-
тона 500 Гц, амплитуда колебаний 0,1 мм.
Определите максимальное ускорение.
5.
Полная энергия тела, совер-
шающего колебательное движение, равна
3 · 10
–5
Дж, максимальная сила, действую-
