Барков Ю.А., Зверев О.М., Перминов А.В. Сборник задач по общей физике

Подождите немного. Документ загружается.

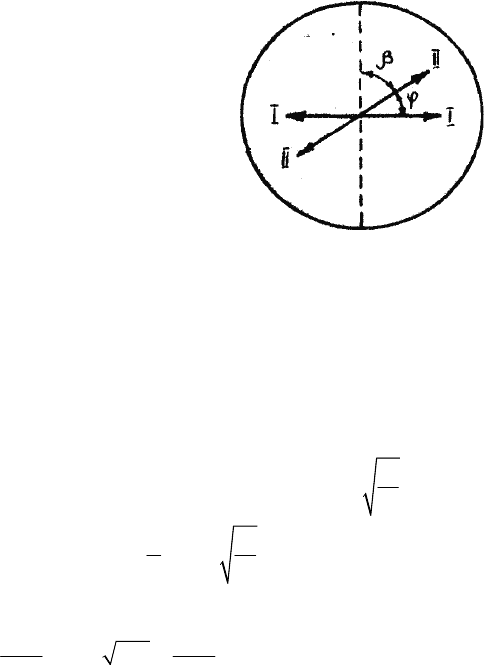
131

дикулярна плоскости колебаний (I–I)

плоскополяризованного света, падаю-

щего на него. Введение кварцевой пла-

стины приводит к повороту плоскости

колебания света на угол

φ = αl, (1)

где l – толщина пластины.

Зная, во сколько раз уменьшится

интенсивность света при прохождении

его через поляроид, определим угол β, который установится между

плоскостью пропускания поляроида и новым направлением (II–II)

плоскости колебаний падающего на поляроид плоскополяризован-

ного света. Для этого воспользуемся законом Малюса: I = I

cos

β.

Заметив, что β = π/2 – φ, можно написать I = I

cos

(π/2 – φ),

или

I = I

sin

φ. (2)

Из равенства (2) с учетом (1) получим

α arcsin

= , откуда

искомая толщина пластины

l = arcsin

. Подставим числовые

значения и произведем вычисления (во внесистемных единицах):

l ===

145

arcsin 1 / 2 мм 0,92 мм

48,9 48,9

Варианты заданий приведены на стр. 377–409.

4.3. КВАНТОВАЯ ОПТИКА

Квантовой оптикой называют раздел физики, в котором изу-

чаются оптические явления на основе представления о свете как

потоке частиц. Согласно теории М. Планка, в дальнейшем развитой

А. Эйнштейном, излучение и поглощение света веществом проис-

ходит конечными порциями, называемыми квантами (фотонами).

132

Подобно частице, фотон обладает релятивистской массой и энерги-

ей. Особенностью фотона является то, что он неделим, движется со

скоростью света и его масса покоя равна нулю. Квантовая теория

позволила решить задачу теплового излучения, объяснить явление

фотоэффекта, эффект Комптона и давление света.

Задачи, связанные с определением массы, импульса или энер-

гии фотона, решаются на основании соответствующих формул. При

этом нельзя забывать, что фотон – релятивистская частица и фор-

мулы классической физики к нему неприменимы. Если в задаче на-

ряду с фотонами рассматриваются другие частицы (например, фо-

тон сталкивается с электроном, протоном и т.п., или требуется

сравнить массу, импульс или энергию фотона с соответствующей

характеристикой частицы) и специально не оговорено, реляти-

вистские они или нет, то нужно вычислить энергию

Е и энергию

покоя

частицы. Если Е < Е

, то частицу можно считать нереляти-

вистской и использовать законы классической физики; если

Е > Е

то необходимо применять формулы специальной теории относи-

тельности.

Задачи на фотоэффект решаются на основании формулы

Эйнштейна и вытекающих из нее соотношений:

– красная граница фотоэффекта – это минимальная частота ν

или максимальная длина волны

, при которых возможен фотоэф-

фект; соответствующая энергия кванта равна работе выхода элек-

трона из поверхности данного металла;

– задерживающее напряжение

(задерживающая разность

потенциалов) – это минимальная разность потенциалов между ано-

дом и катодом, при которой электрическое поле между электродами

достаточно сильное, чтобы не дать фотоэлектронам долететь до

анода; U

по величине равно максимальной кинетической энергии

фотоэлектронов;

– ток насыщения I

– это максимальный ток в цепи при усло-

вии, что катод освещается одним и тем же источником света; I

по

величине равен суммарному заряду всех электронов, испускаемых

катодом в единицу времени.

Задачи на давление света решаются на основании формулы

()

1 ρ

=+. При этом следует помнить, что она справедлива

133

только для случая, если свет падает перпендикулярно поверхности

тела. Часто эту формулу удобно использовать в другой форме запи-

си. Поскольку освещенность

равна энергии, падающей в единицу

времени на единицу плошади тела, то ее можно представить в виде

()

1 ρ

где n – число фотонов с частотой ν, падаюших в единицу времени

на единицу площади поверхности тела.

Если свет падает на поверхность под некоторым углом α,

следует обратить внимание на то, что площадь

S поперечного се-

чения светового пучка и площадь S

на поверхности тела, на кото-

рое падает этот пучок, не равны друг другу, а связаны соотноше-

нием S = S

· cosα.

Основные формулы

Законы теплового излучения

1. Закон Стефана – Больцмана. Энергетическая светимость аб-

солютно черного тела пропорциональна абсолютной температуре

в четвертой степени:

= σT

где σ – постоянная Стефана – Больцмана.

Энергетической светимостью называется величина, численно

равная энергии излучения всех длин волн с единицы поверхности

тела в единицу времени:

эλ

dλ

∞

∫

, где r

– спектральная плотность

энергетической светимости (т.е. энергетическая светимость, прихо-

дящаяся на единичный интервал длин волн).

2. Закон смещения Вина. В спектре излучения абсолютно

черного тела длина волны λ

, на которую приходится максимум

энергии излучения, обратно пропорциональна абсолютной тем-

пературе:

134

где b – постоянная Вина.

Фотоэлектрический эффект

3. Формула Эйнштейна для фотоэффекта:

hν = A + W

max

где hν – энергия фотона, падающего на поверхность металла;

А –

работа выхода электрона; W – максимальная кинетическая энергия

фотоэлектрона, вылетевшего из металла.

Если энергия фотона меньше 5 кэВ, то кинетическая энергия W

может быть определена по классической формуле

max

W =

, где

– масса покоя электрона.

Если энергия фотона больше 5 кэВ, то для вычисления кине-

тической энергии W следует воспользоваться релятивистской фор-

мулой W = (m – m

, или

max

1 β

Wmc





=−



−



, β

4. Максимальная длина волны λ

(минимальная частота коле-

баний ν

), начиная с которой фотоэффект прекращается, называется

красной границей фотоэффекта:

= , или

= , где h – посто-

янная Планка.

Давление света. Фотоны

5. Давление р, производимое светом при нормальном падении

на поверхность с коэффициентом отражения ρ, выражается соотно-

шением

()

1 ρ

=+, или р = ω(1+ ρ), где Е

– энергетическая ос-

вещенность поверхности;

с – скорость распространения света в ва-

кууме; ω – объемная плотность энергии излучения.

135

В случае идеально отражающей (зеркальной) поверхности

коэффициент отражения ρ = 1. В случае идеально поглощающей

поверхности (поверхность абсолютно черного тела) коэффициент

отражения ρ = 0.

6. Энергия ε фотона выражается формулой

εν

h==.

Масса m фотона выражается из закона пропорциональности

массы и энергии следующим образом:

==. Импульс фото-

на

Эффект Комптона

7. При соударении со свободным или слабо связанным (ва-

лентным) электроном фотон передает ему часть своей энергии,

вследствие этого длина волны λ′ рассеянного фотона больше длины

волны λ первичного фотона.

Изменение длины волны дается формулой Комптона

λ′

()

1cos

−= −

где m

– масса покоящегося электрона; θ – угол рассеяния. Величи-

на

Λ=

называется комптоновской длиной волны. При рассея-

нии на электроне Λ = 0,02436 Å = 2,436 · 10

–12

м.

Примеры решения задач

№ 1.

Длина волны, на которую приходится максимум энергии в

спектре излучения абсолютно черного тела, λ

= 0,58 мкм. Определить

энергетическую светимость (излучательность) R

поверхности тела.

Р е ш е н и е.

Энергетическая светимость R

абсолютно черного тела в соот-

ветствии с законом Стефана – Больцмана пропорциональна четвер-

той степени абсолютной температуры и выражается формулой

136

= σТ

, (1)

где σ – постоянная Стефана – Больцмана;

Т – термодинамическая

температура.

Температуру

Т можно вычислить с помощью закона смеще-

ния Вина:

= b/Т. (2)

где b – постоянная закона смещения Вина.

Используя формулы (2) и (1), получим







(3)

Выпишем числовые значения величин, входящих в эту формулу:

σ = 5,67⋅10

–8

Вт/(м

·К

), b = 2,90·10

–3

м· К, λ

= 5,8⋅10

–7

и, подста-

вив числовые значения в формулу (3), произведем вычисления:

−



⋅

=⋅ =



⋅



=⋅ =

72 2

2,90 10

5,67 10 Вт / м

5,8 10

3,54 10 Вт / м 35,4 МВт / м .

№ 2.

Определить максимальную скорость v

max

фотоэлектро-

нов, вырываемых с поверхности серебра: 1) ультрафиолетовыми

лучами с длиной волны λ

= 0,155 мкм; 2) γ-лучами с длиной вол-

ны λ

= 1 пм.

Р е ш е н и е.

Максимальную скорость фотоэлектронов можно определить

из уравнения Эйнштейна для фотоэффекта

ε =

А + W

max

, (1)

где ε – энергия фотона, падающего на поверхность металла;

А – ра-

бота выхода электрона из металла;

max

– максимальная кинетиче-

ская энергия фотоэлектрона.

Энергия фотона вычисляется также по формуле

ε = h

с/λ, (2)

137

где h – постоянная Планка; с – скорость света в вакууме; λ – дли-

на волны.

Кинетическая анергия электрона может быть выражена или

по классической формуле

W =

(3)

или по релятивистской

1 β





=−



−



(4)

в зависимости от того, какая скорость сообщается фотоэлектрону.

Скорость фотоэлектрона зависит от энергии фотона, вызы-

вающего фотоэффект: если энергия ε фотона много меньше энергии

покоя

электрона, то может быть применена формула (3), если же ε

сравнима по величине с

, то вычисление по формуле (3) приводит

к ошибке, поэтому нужно пользоваться формулой (4).

1. Вычислим энергию фотона ультрафиолетовых лучей по

формуле (2):

−

⋅⋅⋅

==⋅

⋅

34 8

-18

6,63 10 3 10

Дж 1,28 10 Дж

1,55 10

или

−

⋅

1,28 10

эВ 8 эВ

1,6 10

Полученная энергия фотона (8 эВ) много меньше энергии по-

коя электрона (0,51 МэВ). Следовательно, для данного случая кине-

тическая энергия фотоэлектрона в формуле (1) может быть выраже-

на по классической формуле (3): ε

= А +

max

откуда

()

max

2 ε

−

= . (5)

Выпишем числовые значения величин: ε

= 1,28 10

–18

Дж (вы-

числено выше),

А = 4,7 эВ = 4,7 · 1,6 10

–19

Дж, m

= 9,11 10

–31

кг.

138

Подставив числовые значения в формулу (5), найдем

()

18 18

max

21,2810 0,7510

1,08 10

9,11 10

−−

−

⋅−⋅

==⋅

⋅

2. Вычислим энергию фотона γ-лучей:

34 8

-13

6,63 10 3 10

εДж

1,99 10

Дж

−

⋅⋅⋅

== = ⋅

или

1,99 10

εэВ

1,24 10

эВ

1,24

МэВ

1, 6 10

−

⋅

==⋅=

⋅

Работа выхода электрона (

А = 4,7 эВ) пренебрежимо мала

по сравнению с энергией фотона (ε

= 1,24 МэВ), поэтому можно

принять, что максимальная кинетическая энергия электрона рав-

на энергии фотона: W

max

= ε

= 1,24 МэВ. Так как в данном случае

кинетическая энергия электрона больше его энергии покоя, для

вычисления скорости электрона следует взять релятивистскую

формулу кинетической энергии (4). Из этой формулы найдем

()

EWW

Заметив, что v = cβ и W

max

= ε

, получим

()

022

max

2 εε

Подставим числовые значения величин и произведем вычис-

ления:

()

max

20,51 1,241,24

310

2,85 10

0,51 1,24

⋅+

=⋅ = ⋅

№ 3. В результате эффекта Комптона фотон при соударении

с электроном был рассеян на угол θ = 90°. Энергия рассеянного фо-

тона ε

= 0,4 МэВ. Определить энергию фотона ε

до рассеяния.

Р е ш е н и е.

Для определения энергии первичного фотона воспользуемся

формулой Комптона

∆λ

2sin

, (1)

139

где ∆λ – изменение длины волны фотона в результате рассеяния

на свободном электроне, ∆λ = λ

– λ

; h – постоянная Планка; m

–

масса покоя электрона;

с – скорость света в вакууме; θ – угол

рассеяния фотона.

Формулу (1) преобразуем следующим образом: 1) заменим

в ней ∆λ на λ

– λ

; 2) выразим длины волн λ

и λ

через энергии

и ε

соответствующих фотонов, воспользовавшись формулой

ε = hc/λ; 3) умножим числитель и знаменатель правой части фор-

мулы на

с. Тогда получим

21 0

2sin .

εε

hc hc hc

−=

Сократим на h

с и выразим из полученной формулы искомую

энергию:

220

22 2

02 02

εε

θθ

2ε sin 2ε sin

mc E

−−

(2)

где

– энергия покоя электрона, Е

= m

Вычисления по формуле (2) удобно вести во внесистемных

единицах. Взяв из таблицы значение энергии покоя электрона

в мегаэлектрон-вольтах и подставив числовые данные, получим

⋅

−⋅

0,4 0,51

1,85 МэВ

0,51 2 0,4sin

№ 4. Пучок параллельных лучей монохроматического света

с длиной волны λ = 663 нм падает нормально на плоскую зеркаль-

ную поверхность. Поток излучения Ф = 0,6 Вт. Определить: 1) силу F

давления, испытываемую этой поверхностью; 2) число N

фотонов,

ежесекундно падающих на поверхность.

Р е ш е н и е.

Сила светового давления на поверхность равна произведе-

нию светового давления р на площадь S поверхности:

F =

рS. (1)

Световое давление может быть найдено по формуле

()

=+, (2)

140

где Е

– энергетическая освещенность (облученность); c – скорость

света в вакууме; ρ – коэффициент отражения. Подставляя выраже-

ние (2) давления света в формулу (1), получим

()

=+. (3)

Энергетическая освещенность Е

есть величина, численно

равная энергии, падающей на единичную площадку в единицу вре-

мени. Произведение Е

на S есть величина, численно равная энер-

гии, падающей на данную площадку S в единицу времени, т.е. поток

излучения Ф = Е

S. С учетом этого формула (3) примет вид

()

=+. (4)

Величины, входящие в формулу (4), выпишем в единицах

СИ: Ф = 0,6 Вт, с = 3·10

м/с, ρ = 1 (поверхность зеркальная).

После подстановки этих величин в формулу (4) получим

()

F =+=⋅

⋅

-9

0,6

11 410H

310

Произведение энергии ε одного фотона на число фотонов

, падающих на поверхность в единицу времени, равно мощно-

сти излучения, т.е. потоку излучения: Ф = εN

, а так как энергия

фотона ε = hc/λ, то

= , откуда

Фλ

= . (5)

Выпишем величины, входящие в формулу (5), в единицах СИ:

Ф = 0,6 Вт, λ = 6,63⋅10

–7

м, h = 6,63⋅10

–34

Дж·с, с = 3⋅10

м/с. Под-

ставим полученные значения в расчетную формулу и произведем

вычисления:

118-1

34 8

0,6 6,63 10

210

6,63 10 3 10

N с

−

⋅⋅

==⋅

⋅⋅⋅