Барков Ю.А., Зверев О.М., Перминов А.В. Сборник задач по общей физике

Подождите немного. Документ загружается.

121

ты максимумов и минимумов интерференционной картины на экра-

не можно найти следующим образом:

– ввести систему координат и выбрать произвольную точку на

экране;

– провести в эту точку лучи от обоих источников;

– из геометрических соображений найти пути S

и S

волн,

распространяющихся вдоль этих лучей, выразив их через координа-

ты точки на экране и расстояние до экрана;

– найти оптические пути n

и п

волн;

– найти оптическую разность хода волн;

– если требуется определить координаты максимумов, то по-

лученную оптическую разность хода следует приравнять к величи-

не, равной целому числу длин волн (или четному числу длин полу-

волн); если требуется определить координаты минимумов, то раз-

ность хода лучей следует приравнять величине, равной нечетному

числу длин полуволн;

– найти координаты максимумов и минимумов интерферен-

ционной картины, расстояние между интерференционными полоса-

ми и ширину интерференционных полос.

При интерференции в тонких пленках оптическая разность

хода интерферирующих волн возникает за счет дополнительного

расстояния, пройденного одной из них. В таких задачах следует

учитывать, что одна из интерферирующих волн отражается от гра-

ницы раздела сред. Если отражение происходит от среды с показа-

телем преломления большим, чем среда, в которой распространяет-

ся свет, то фаза отраженной волны изменится на π радиан, что соот-

ветствует оптическому пути, равному ± λ/2. Если отражение света

происходит от среды с меньшим показателем преломления, то фаза

отраженной волны не меняется.

Задачи на

дифракцию также делятся на две группы соответст-

венно двум видам дифракции – дифракции Френеля и дифракции

Фраунгофера.

Для решения задач на дифракцию Френеля (или дифракцию

в расходящихся лучах) необходимо освоить метод зон Френеля, по-

зволяющий путем геометрических построений установить законо-

мерности распределения интенсивности волны на круглом отвер-

стии или круглом диске.

122

Большинство задач на дифракцию Фраунгофера (или дифрак-

цию в параллельных лучах) связано с дифракционной решеткой –

совокупностью большого числа щелей одинаковой ширины, разде-

ленных одинаковыми по ширине непрозрачными промежутками.

Из основной формулы дифракционной решетки d · sinφ = ± kλ мож-

но сделать три вывода: 1) число главных максимумов ограничено,

и наибольшее значение k определяется условием k

max

= d/λ, так как

значение синуса не может превышать единицы; 2) дифракционная

картина является симметричной относительно первичного луча,

проходящего через главный фокус линзы; 3) положения главных

максимумов, за исключением только центрального максимума

(k = 0), зависят от длины волны света. Из последнего вывода следу-

ет, что дифракционная решетка обладает способностью разлагать

падающий на нее свет по длинам волн. Если, к примеру, на решетку

падает белый свет, то все дифракционные максимумы, кроме нуле-

вого, будут окрашены, т.е. разложатся в спектр, причем фиолетовый

участок спектра будет располагаться ближе к центру дифракцион-

ной картины, а красный участок окажется дальше от ее центра.

Задачи на

поляризацию в методическом плане не представля-

ют особой трудности. Достаточно хорошо разобраться с природой

поляризованного света и двумя законами – законом Малюса и зако-

ном Брюстера.

Основные формулы

Интерференция света

1. Скорость света в среде

= где с – скорость света в ва-

кууме; n – показатель преломления среды.

2. Оптическая длина пути луча L = n · l, где l – геометриче-

ская длина пути луча в среде с показателем преломления n.

3. Если один луч проходит путь длиной l

в среде с пока-

зателем преломления n

, а другой луч – путь l

в среде с показа-

телем преломления n

, то оптическая разность хода этих лучей

∆ = n

– n

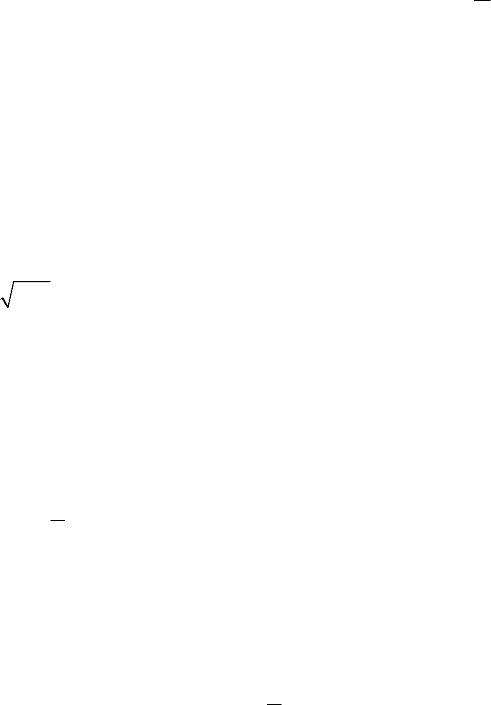
123

4. Разность фаз колебаний ∆φ связана с оптической разностью

хода ∆ интерферирующих волн соотношением

∆

∆=

, где λ –

длина световой волны в вакууме.

5. Условие максимального усиления света в результате ин-

терференции ∆ = ± kλ, (k = 0, 1, 2, …).

Условие максимального ослабления света

∆ = ±(2k + 1)λ/2, (k = 0, 1, 2, …).

Дифракция света

6. Радиусы зон Френеля в случае плоского волнового фрон-

та

rkr

= , где r

– радиус зоны, k – номер зоны (k = 1, 2, …);

– расстояние от круглого отверстия в непрозрачном экране до

точки наблюдения, расположенной на оси отверстия; λ – длина

световой волны.

7. При дифракции параллельного пучка лучей монохромати-

ческого света на одной узкой длинной щели:

а) направления, в которых амплитуда колебаний дифраги-

рованных лучей минимальна, определяются из условия

sinφ

; 1, 2,3,...,

akkk=± =± =

где а – ширина щели; φ – угол

отклонения лучей от нормали к плоскости щели, определяющий

направление на дифракционный минимум; k – порядковый номер

минимума; λ – длина световой волны;

б) направления, по которым амплитуда колебаний дифраги-

рованных лучей после их интерференции максимальна, определя-

ются по формуле

sinφ

(2 1) ; 1, 2,3,....

akk

′

=± + =

8. При дифракции на плоской дифракционной решетке на-

правления, в которых наблюдаются максимумы света, определя-

ются из условия

(a + b) sinφ = ± kλ; k = 0, 1, 2, …, где

а – ширина прозрачной

полоски (щели); b – ширина непрозрачного штриха; d – период ре-

шетки (или постоянная решетки), d = (

а + b); φ – угол между нор-

124

малью к поверхности решетки и направлением дифрагированных

лучей; k – порядковый номер дифракционного максимума.

9. Разрешающая сила дифракционной решетки

R =

∆

где

∆λ – наименьшая разность длин волн двух соседних спектраль-

ных линий (λ и λ + ∆λ), при которой эти линии могут быть видны

раздельно в спектре, полученном посредством данной решетки.

Разрешающая сила R решетки тем больше, чем больше

штрихов решетка содержит и чем больше порядковый номер ди-

фракционного максимума: R = kN, где N – полное число штрихов

решетки.

10. Угловая дисперсия решетки

()

dφ

dλ

cos

При дифракции рентгеновских лучей на кристаллической

решетке направления, в которых имеет место зеркальное отраже-

ние (дифракционный максимум), определяются из уравнения

Вульфа – Бреггов: 2d · sinθ = kλ, где d – расстояние между атомны-

ми плоскостями кристалла; θ – угол скольжения (угол между на-

правлением пучка параллельных рентгеновских лучей, падающих

на кристалл, и гранью кристалла).

Поляризация света

11. Закон Брюстера. Луч, отраженный от поверхности диэлек-

трика, максимально поляризован, если тангенс угла падения i

луча

на поверхность раздела двух сред равен относительному показате-

лю преломления n

второй среды относительно первой: tgi

= n

Закон Брюстера неприменим в случае отражения от поверхности

проводников.

12. Закон Малюса. Интенсивность I плоскополяризованного

света, прошедшего через анализатор, прямо пропорциональна квад-

рату косинуса угла α между направлением колебаний света, падаю-

щего на анализатор, и направлением колебаний, которые анализа-

тор пропускает без ослабления: I = I

cos

α, где I

– интенсивность

света, падающего на анализатор.

125

13. Вращение плоскости поляризации. Угол поворота плоско-

сти поляризации монохроматического света:

а) в твердых телах φ = α · d, где α – постоянная вращения;

d – толщина пластинки, вырезанной из твердого тела;

б) в чистых жидкостях φ = [α] · ρ · l, где [α] – удельное враще-

ние; ρ – плотность жидкости; l – длина столбика жидкости;

в) в растворах φ = [α] ·

С · l, где С – концентрация раствора

(масса активного вещества в единице объема раствора).

Примеры решения задач

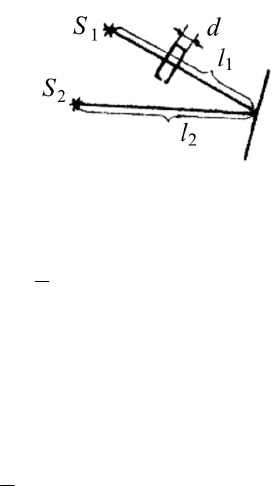
№ 1.

От двух когерентных источников S

и S

(λ = 0,8 мкм)

лучи попадают на

экран. На экране наблюдается интерференцион-

ная картина. Когда на пути одного из лучей перпендикулярно ему

поместили мыльную пленку (n = 1,33), интерференционная картина

изменилась на противоположную. При какой наименьшей толщине

min

пленки это возможно?

Р е ш е н и е.

Изменение интерференционной

картины на противоположную означа-

ет, что на тех участках, где наблюда-

лись интерференционные максимумы,

стали наблюдаться интерференцион-

ные минимумы. Такой сдвиг интерфе-

ренционной картины возможен при

изменении оптической разности хода лучей на нечетное число по-

ловин

длин волн, т.е.

∆

– ∆

= (2k + 1)

, (1)

где ∆

– оптическая разность хода лучей до внесения пленки;

∆

– оптическая разность хода тех же лучей после внесения

пленки; k = 0, ± 1, ±2, ….

Наименьшей толщине d

min

пленки соответствует k = 0. При

этом формула (1) примет вид

∆

– ∆

. (2)

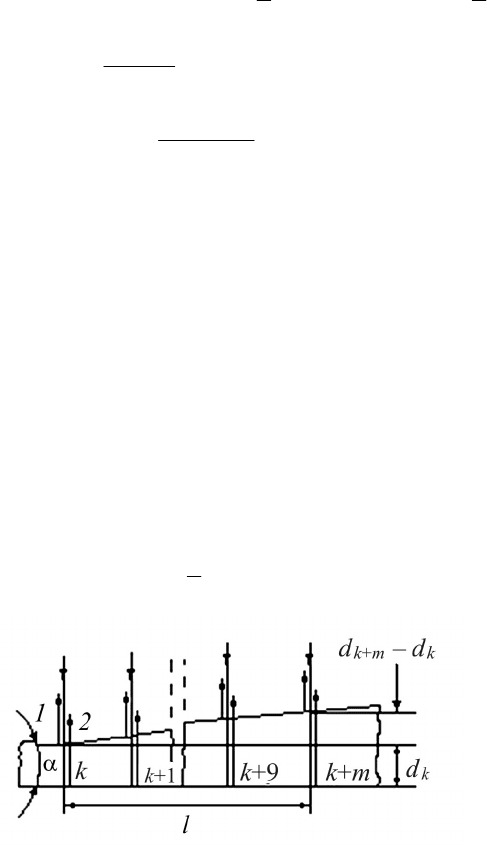
126

Выразим оптические разности хода ∆

и ∆

. Из рисунка сле-

дует: ∆

= l

– l

, ∆

= [(l

– d

min

) + nd

min

] – l

= (l

– l

) + d

min

(n – 1).

Подставим выражения ∆

и ∆

в формулу (2):

– l

) + d

min

(n – 1) – (l

– l

) =

, или d

min

(n – 1) =

Отсюда

()

min

−

. Подставив числовые значения, найдем

()

min

d ==

−

0,8

1,21

21,33 1

мкм.

№ 2. На стеклянный клин с малым углом нормально к его

грани падает параллельный пучок лучей монохроматического света

с длиной волны λ = 0,6 мкм. Число m возникающих при этом ин-

терференционных полос, приходящихся на 1 см, равно 10. Опреде-

лить угол α клина.

Р е ш е н и е.

Лучи, падая нормально к грани клина, отражаются как от

верхней, так и от нижней грани. Эти лучи когерентны. Поэтому на

поверхности клина будут наблюдаться интерференционные полосы.

Так как угол клина мал, то отраженные лучи 1 и 2 (рисунок) будут

практически параллельны.

Темные полосы видны на тех участках клина, для которых

разность хода лучей кратна нечетному числу половин длин волн:

()

k∆= + (k = 0, ± 1, ± 2, …). (1)

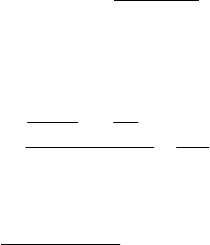
127

Разность хода ∆ двух лучей складывается из разности оптиче-

ских длин путей (2dncosi

) этих лучей и половины длины волны λ/2.

Величина λ/2 представляет собой добавочную разность хода, воз-

никшую при отражений луча 1 от оптически более плотной среды.

Подставляя в формулу (1) значение разности хода ∆ лучей, получим

n cosi

+ λ/2 = (2k +1)λ/2, (2)

где n – показатель преломления стекла (n = 1,6); d

– толщина клина

в том месте, где наблюдается темная полоса, соответствующая но-

меру k; i – угол преломления второго луча.

Согласно условию, угол падения равен нулю, следовательно,

и угол преломления i

равен нулю, а соs i

= 1. Раскрыв скобки

в правой части равенства (2), после упрощения получим

n = kλ. (3)

Пусть произвольной темной полосе k-гo номера соответствует

толщина d

клина, а темной полосе (k + m)-го номера – толщина d

k+m

клина. Тогда из рисунка, учитывая, что m полос укладывается на

расстоянии l, найдем

tgα = sinα =

−

(4)

Выразим из (3) d

и d

k+m

и подставим их в формулу (4).

Затем, учитывая, что из-за малости угла α sinα ≈ α, получим

λλ

km k

lnl

−

Подставляя

числовые значения физических величин, найдем

−

+⋅

==⋅

⋅⋅

-4

10 0,6 10

210 рад.

21,510

№ 3.

На дифракционную решетку нормально к ее поверхно-

сти падает монохроматический свет. Период решетки d = 2 мкм.

Какого наибольшего порядка дифракционный максимум дает эта

решетка в случае красного (λ

= 0,7 мкм) и в случае фиолетового

(λ

= 0,41 мкм) света?

128

Р e ш е н и е.

На основании известной формулы дифракционной решетки

напишем выражение порядка дифракционного максимума:

sinφ

m = , (1)

где d – период решетки; φ – угол между направлением

на дифрак-

ционный максимум и нормалью к решетке; λ – длина волны моно-

хроматического света. Так как sinφ не может быть больше 1, то, как

следует из формулы (1), число m не может быть больше d/λ, т.е.

m ≤ d/λ. (2)

Подставив в формулу (2) числовые значения, получим: для крас-

ных лучей m ≤ 2/0,7 = 2,86; для фиолетовых лучей m ≤ 2/0,41 = 4,88.

Если учесть, что порядок максимумов является целым чис-

лом, то для красного света m

max

= 2 и для фиолетового m

max

= 4.

№ 4. Естественный луч света падает на полированную по-

верхность стеклянной пластины, погруженной в жидкость. Отра-

женный от пластины луч образует угол ϕ = 97°

с падающим лучом

(рисунок). Определить показатель преломления n

жидкости, если

отраженный свет максимально поляризован.

Р е ш е н и е.

Согласно закону Брюстера

луч света, отраженный от диэлек-

трика, максимально поляризован

в том случае, если тангенс угла па-

дения численно равен относитель-

ному показателю преломления:

tg i

= n

, где n

– показатель пре-

ломления второй среды (стекла)

относительно первой (жидкости).

Относительный показатель преломления равен отношению

абсолютных показателей преломления. Следовательно, tg i

= n

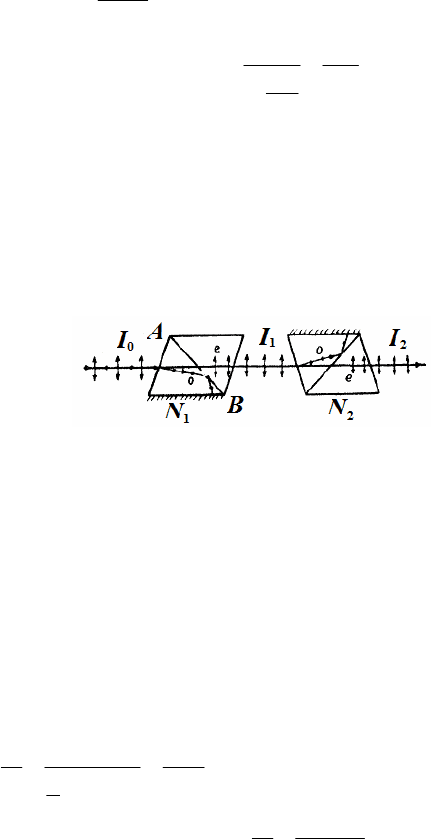
129

Так как угол падения равен углу отражения, то i

= φ/2 и, следова-

тельно, tg φ/2 = n

, откуда

tgφ

n = .

Подставив числовые значения, получим

1, 5 1, 5

1, 33

1,13

n ===

№ 5. Два николя N

и N

расположены так, что угол между их

плоскостями пропускания составляет α = 60°. Определить, во

сколько раз уменьшится интенсивность I

естественного света:

1) при прохождении через один николь N

; 2) при прохождении че-

рез оба николя. Коэффициент поглощения света в николе k = 0,05.

Потери на отражение света не учитывать.

Р е ш е н и е.

1. Естественный свет,

падая на грань призмы ни-

коля (рисунок), расщепляет-

ся вследствие двойного лу-

чепреломления на два луча:

обыкновенный и необыкновенный. Оба луча одинаковы по интенсивно-

сти и полностью поляризованы. Плоскость колебаний необыкновенного

луча лежит в плоскости чертежа (плоскость главного сечения). Плос-

кость колебаний обыкновенного луча перпендикулярна плоскости чер-

тежа. Обыкновенный луч О вследствие полного внутреннего отражения

от границы

АВ отбрасывается на зачерненную поверхность призмы

и поглощается ею. Необыкновенный луч

е проходит через призму,

уменьшая свою интенсивность вследствие поглощения: I

·I

(1 – k).

Относительное уменьшение интенсивности света получим,

разделив интенсивность I

естественного света, падающего на пер-

вый николь, на интенсивность I

поляризованного света:

()

−

. (1)

Подставив в (1) числовые значения, найдем

2,1.

10,05

−

Таким образом, интенсивность уменьшается в 2,1 раза.

130

2. Плоскополяризованный луч света интенсивности I

падает

на второй николь N

и также расщепляется на два луча различной

интенсивности: обыкновенный и необыкновенный. Обыкновенный

луч полностью поглощается призмой, поэтому интенсивность его

нас не интересует. Интенсивность необыкновенного луча I

, вы-

шедшего из призмы N

, определяется законом Малюса (без учета

поглощения света во втором николе): I

= I

cos

α, где α – угол меж-

ду плоскостью колебаний в поляризованном луче и плоскостью

пропускания николя N

Учитывая потери интенсивности на поглощение во втором

николе, получим I

= I

(1 – k)cos

α.

Искомое уменьшение интенсивности при прохождении света

через оба николя найдем, разделив интенсивность I

естественного

света на интенсивность I

света, прошедшего систему из двух ни-

колей:

()

1cosα

II k

−

Заменяя отношение I

его выражением по формуле (1),

получим

()

1cosα

−

Подставляя данные, произведем вы-

числения:

()

8,86.

10,05cos60

−°

Таким образом, после прохождения света через два николя

интенсивность его уменьшится в 8,86 раза.

№ 6.

Плоскополяризованный монохроматический луч света

падает на поляроид и полностью им гасится. Когда на пути луча

поместили кварцевую пластину, интенсивность I луча света после

поляроида стала равна половине интенсивности луча, падающего на

поляроид. Определить минимальную толщину кварцевой пластины.

Поглощением и отражением света поляроидом пренебречь, посто-

янную вращения кварца α принять равной 48,9 град/мм.

Р е ш е н и е.

Полное гашение света поляроидом означает, что плоскость

пропускания поляроида (пунктирная линия на рисунке) перпен-