Барков Ю.А., Зверев О.М., Перминов А.В. Сборник задач по общей физике
Подождите немного. Документ загружается.


91
Учитывая, что заряд после присоединения второго конденса-
тора остается прежним, выразим разность потенциалов U
2
следую-
щим образом:
11
2
12 12
qCU
U
CC CC
==
++
.
Подставим выражение U
2
в формулу (3):
()
()
()
22
2222
1211
11 11 1 1
2
12
12
ССCU
С U С UCU
W
CC
CC
+
′
=− =−
+
+
222
2
.
После преобразований имеем
12
2
1
12
1 CC
W
U
CC
′
=
+
2
.
Подставим числовые значения и вычислим W´:
мДж
.
W
−−
−−
⋅⋅⋅
′
=⋅=
⋅+⋅
56
66
1310 510
1600 1,5
23 10 5 10
Варианты заданий приведены на стр. 275–310.
3.2. ПОСТОЯННЫЙ ТОК
Задачи на постоянный ток можно разделить на два типа:
вычисление сопротивлений, сил токов или напряжений на каком-
либо участке цепи; задачи на работу, мощность и тепловое дей-
ствие тока.
Из задач первого типа можно выделить вспомогательную
группу – задачи на вычисление сопротивлений отдельных провод-
ников и соединений из них. Если в условии задачи указано, из ка-
кого материала изготовлен проводник, или приводятся сведения
о его геометрических размерах или массе, то для нахождения не-
известной величины нужно воспользоваться формулой сопротив-
ления и соотношением между массой, объемом и плотностью про-
водника. Решение задач на вычисление сопротивлений сложных
соединений нужно начинать с анализа схемы и отыскания в ней
каких-нибудь двух (иногда более) проводников, соединенных друг

92
с другом последовательно или параллельно. Их сопротивление
следует заменить одним эквивалентным сопротивлением, исполь-
зуя соответствующие формулы:
R
посл
=
∑
=
n
i
i
R
1
и
парал
1
11
,
n
i
i
R
R
=
=
∑
и получить упрощенную схему. В схемах, представляющих собой
комбинацию последовательно и параллельно включенных провод-
ников, этот прием нужно применять несколько раз и таким образом
найти общее сопротивление.
При решении задач на определение силы тока, напряжения
или сопротивления на каком-либо участке цели следует:
а) начертить схему и указать на ней все элементы цепи – ис-
точники тока, резисторы и конденсаторы;
б) установить, какие элементы цепи включены последова-
тельно, какие – параллельно;
в) расставить токи и напряжения на каждом участке цепи;
г) используя законы Ома, установить связь между токами
и напряжениями (ЭДС). В результате получается система уравне-
ний, полностью отражающая условия задачи и позволяющая опре-
делить искомую величину.
Задачи второго типа можно, в свою очередь, разбить на три
группы. К первой группе относятся задачи на расчет электрической
цепи, аналогичные рассмотренным выше. Для их решения состав-
ляют те же уравнения законов Ома, но к ним добавляют формулы
мощности (работы). Особое внимание следует обратить на выбор
исходной формулы мощности. Если речь идет о мощности, выде-
ляемой на участке цепи, нужно пользоваться формулой
P = I ⋅ U = I
2
⋅ R = U
2
/R.
Мощность, развиваемая источником, – полная мощность, оп-
ределяется по формуле
P
0
= I ⋅ ε =
2
ε
Rr
+
,

93
а мощность во внешней цепи источника тока
P = I ⋅ ε
– I
2
⋅ r =
()
2
2
ε
R
R
r
⋅
+
.
Ко второй группе относятся задачи на тепловое действие
тока. Основным расчетным соотношением в них является закон
Джоуля – Ленца:
Q = I
2
⋅ R ⋅ t.
Если участок цепи не содержит источников тока, то количе-
ство теплоты, выделяющееся на этом участке, можно определять по
формуле
Q = I ⋅ U ⋅ t =
2
U
t
R
.
Третью, небольшую, группу составляют задачи о превраще-
нии электрической энергии в механическую, тепловую и химиче-
скую при работе электромашин постоянного тока. Решение таких
задач основано на применении уравнения закона сохранения и пре-
вращения энергии.
Основные формулы
1. Сила тока
d
,
d
q
I
t
=
где q – заряд, прошедший через поперечное сечение проводника за
время t.
Плотность тока
j = I/S,
где S – площадь поперечного сечения проводника.
Связь плотности тока со средней скоростью
v
G
упорядочен-
ного движения заряженных частиц
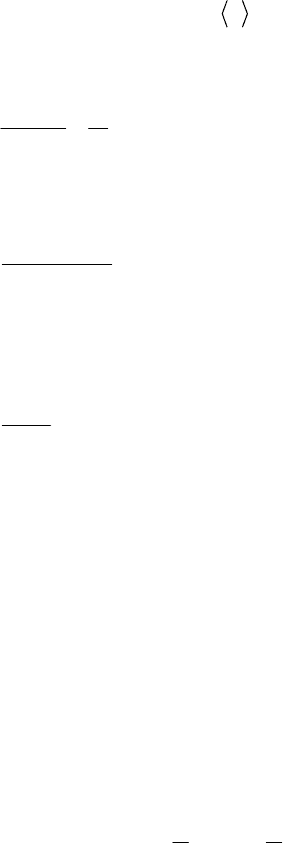
94
jqnv
=
G
G
,
где q – заряд частиц; n – их концентрация.
2.
Закон Ома:
а)
12
φφ
U
I
RR
−
==
– для участка цепи, не содержащего ЭДС
(для однородного участка цепи), где ϕ
1
– ϕ
2
= U – разность потен-
циалов (напряжение) на концах участка цепи; R – сопротивление
участка;
б)
12
(φφ
)
ε
I
R
−±
= – для участка цепи, содержащего ЭДС (для
неоднородного участка цепи), где ε – ЭДС источника тока; R – пол-
ное сопротивление участка (сумма внешних и внутренних сопро-
тивлений). Знаки «+» или «–» выбираются в зависимости от поляр-
ности включения источника.
в)
ε
I
Rr
=
+
– для замкнутой (полной) цепи, где R – сопротив-
ление внешней цепи; r – сопротивление внутреннее (сопротивление
источника тока).
3.
Правила Кирхгофа:
а)
0
i
I =
∑
– первое правило;
б) ε
i
i
i
IR=
∑∑
– второе правило,
где
i
I
∑
– алгебраическая сумма сил токов, сходящихся в узле;
ii
IR
∑
– алгебраическая сумма произведений сил токов на сопро-
тивления участков замкнутого контура; ε
i
∑
– алгебраическая
сумма ЭДС в замкнутом контуре.
4.
Сопротивление R и проводимость G однородного про-
водника:
R =
ρ
l
S
, G =γ
S
l
,
где ρ – удельное сопротивление; γ – удельная проводимость; l – дли-
на проводника; S – площадь поперечного сечения.

95
Зависимость удельного сопротивления от температуры:
()
0
ρρ
1
α
t
=+
,
где α – температурный коэффициент сопротивления; t – температу-
ра по шкале Цельсия.
Сопротивление системы проводников:
а)
i
RR
=
∑
– при последовательном соединении;
б)
i
R
R
=
∑
11
– при параллельном соединении,
где R
i
– сопротивление i-го проводника.
5.
Работа тока:
2
2
dd dd
U
AIUtIRt t
R
=⋅⋅ = = .
Закон Джоуля – Ленца (тепловое действие тока):
2
dd d,
QAIRt
==
где dQ – количество теплоты, выделяющейся в проводнике; dt – про-
межуток времени, в течение которого выделялось тепло.
Мощность тока полной цепи
P = I
ε.
Мощность тока на внешнем участке цепи
P = IU = I
2
R = U
2
/R.
Закон Ома в дифференциальной форме
γ
j
E
=
G
G
.
Закон Джоуля – Ленца в дифференциальной форме
w =
γ E
2
,
где w – объемная плотность тепловой мощности (количество тепла,
выделяющегося в единице объема за единицу времени).

96
Примеры решения задач
№ 1.
Сила тока в проводнике равномерно нарастает от I
0
= 0
до I = 2 А в течение времени τ = 5 с. Определите заряд, прошедший
по проводнику.
Р е ш е н и е.
Так как сила тока в проводнике изменяется, воспользоваться
для подсчета заряда формулой Q= I · t нельзя. Поэтому возьмем
дифференциал заряда dQ = I · dt и проинтегрируем:
τ
0
d
Q
I
t
=⋅
∫
. (1)
В силу равномерного нарастания тока I = kt, где k – коэффи-
циент пропорциональности. Очевидно,
0
ττ
I
I
I
k
−
==
и
1
ddd.
τ
Qktt tt
=⋅= ⋅
Проинтегрировав, получим
τ
0
1 τ
d
τ
2
I
Qtt=⋅=
∫
.
Подставим числовые значения:
25
2
Q
⋅
==
5
Кл.
№ 2.
Найти полное сопротивление схемы (а), если она вклю-
чена в цепь в точках 1 и 2. R
1
= R
2
= R
3
= R
4
= R
5
= R.
Р е ш е н и е.
Очевидно, что сопротивления R
3
и R
5
соединены последова-
тельно, так как в точке 4 разветвлений нет. Определив их общее со-
противление R
Э1
= 2R, представим схему в виде б. Теперь можно
выделить параллельно соединенные сопротивления R
Э1
и R
4
. Сопро-
тивление между точками схемы 2 и 3 R
Э2
=
14
14
Э
Э
RR
RR
⋅
+
=
22
.
23
RR
R
RR
⋅
=
+
97
Схему можно представить в виде в. Тогда имеем последователь-
но соединенные сопротивления R
Э2
и R
2
. Их общее сопротивле-
ние R
Э3
= R
Э2
+ R
2
=
5
3
R
. Наконец, общее сопротивление всей
схемы (схема г) равно сопротивлению параллельно включенных
сопротивлений R
Э3
и R
1
:
31
12
31
5/3 5
5/3 8
Э
Э
RR RR
RR
RR RR
⋅⋅⋅
== =
+⋅+
.
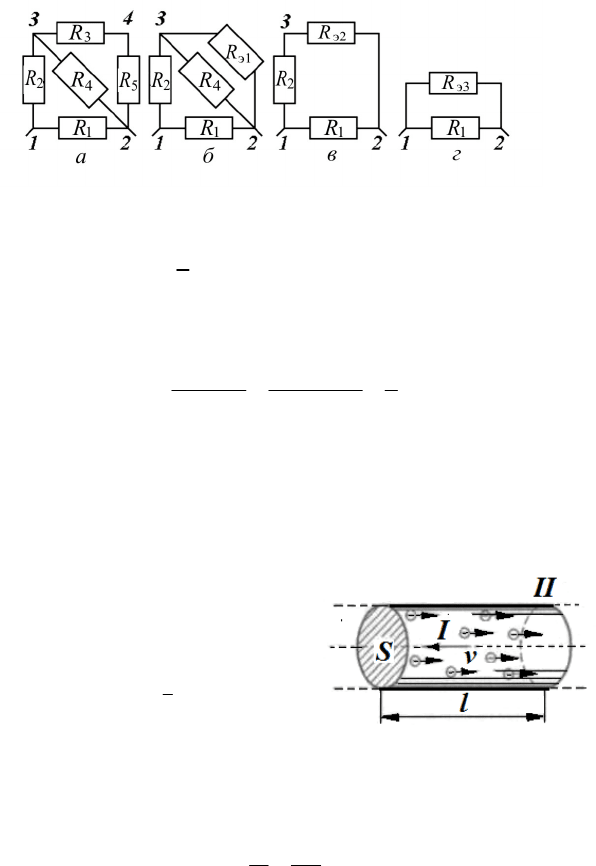
№ 3.
По железному проводнику, диаметр d сечения которого
равен 0,6 мм, течет ток 16 А. Определите среднюю скорость <v>
направленного движения электронов, считая, что концентрация n
свободных электронов равна концентрации п' атомов проводника.
Р е ш е н и е.
Средняя скорость направлен-
ного (упорядоченного) движения
электронов определяется по формуле
<v> =
l
t
, (1)
где t – время, в течение которого все
свободные электроны, находящиеся в отрезке проводника между
сечениями I и II, пройдя через сечение II, перенесут заряд Q = eN
и создадут ток
QeN
I
tt
==
, (2)
где е – элементарный заряд; N – число электронов в отрезке про-
водника; l – его длина.

98
Число свободных электронов в отрезке проводника объемом V
можно выразить следующим образом:
N = n
· V = n · l · S, (3)
где S – площадь сечения.
По условию задачи п = п'. Следовательно,
µ
ρ
/ ρ
AAA
NNN
nn
V
MM
⋅
′
== = =
, (4)
где N
А
– постоянная Авогадро; Vµ – молярный объем металла;
М – молярная масса металла; ρ – его плотность.
Подставив последовательно выражения п из формулы (4) в ра-
венство (3) и N из формулы (3) в равенство (2), получим
ρ
A
NlSe
I
Mt
⋅⋅⋅⋅
=
⋅
.
Отсюда найдем
ρ
A
IMt
l
NSe
⋅⋅
=
⋅⋅⋅
.
Подставив выражение I в формулу (1), сократив на t и выра-
зив площадь S сечения проводника через диаметр d, найдем сред-
нюю скорость направленного движения электронов:
2
4
πρ
A
IM
v
d
N
e
⋅
=
⋅⋅⋅
.
Произведем по этой формуле вычисления:
3
3
623 9 19
4165610
4,2 10
3,14 0,36 10 6 10 98 10 1,6 10
v
−
−
−−−
⋅⋅⋅
==⋅
⋅⋅⋅⋅⋅⋅⋅⋅
м/с.
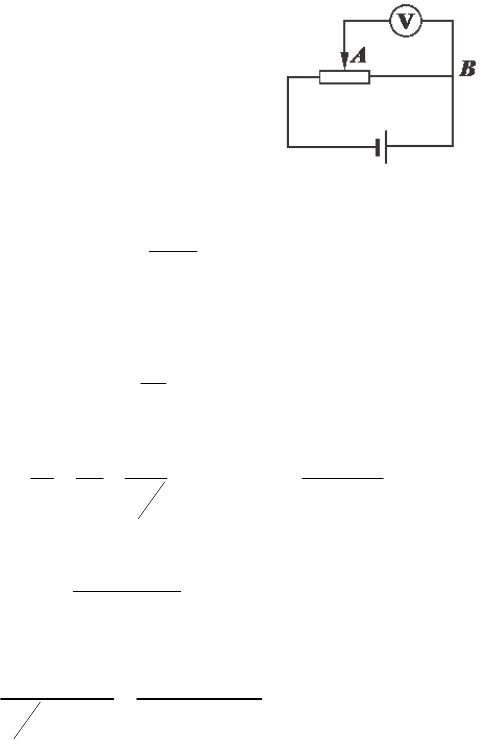
№ 4. Потенциометр с сопротивлением R
п
= 100 Ом подклю-
чен к батарее, ЭДС которой ε = 160 В и внутреннее сопротивление
r = 50
Ом. Определить показание вольтметра с сопротивлением
R
v
= 500 Ом, соединенным с одной из клемм потенциометра и под-
вижным контактом, установленным посередине потенциометра.
99
Какова разность потенциалов между теми же точками потенцио-
метра при отключении вольтметра?
Р е ш е н и е.
Показание U
1
вольтметра, подключенного к точкам А и В
(
рисунок), определяется по формуле
U
1
= I
1
R
1
, (1)
где I
1
– сила тока в неразветвленной части
цепи; R
1
– сопротивление параллельно со-
единенных вольтметра и половины потен-
циометра.
Силу тока I
1
найдем по закону Ома
для всей цепи:
1
ε
I
Rr
=
+
, (2)
где R – сопротивление внешней цепи.
Внешнее сопротивление R есть сумма двух сопротивлений:
1
.
п
R
R
R=+
2
(3)
Сопротивление R
1
параллельного соединения может быть
найдено по формуле
1
11 1
2
п
V
R
RR
=+
, откуда
1
2
п V
п V
RR
R
RR
=
+
.
Подставив числовые значения, найдем
1
R
⋅
==
+⋅
100 500
45,5
100 2 500
Ом.
Из выражений (2) и (3) определим силу тока:
1
1
ε
2
п
I
R
Rr
== =
++
++
150
1,03
50 45,5 50
А.
Если подставить значения I
1
и R
1
в формулу (1), то можно оп-
ределить показание вольтметра: U
1
= 1,03 · 45,5 В = 46,9 В.
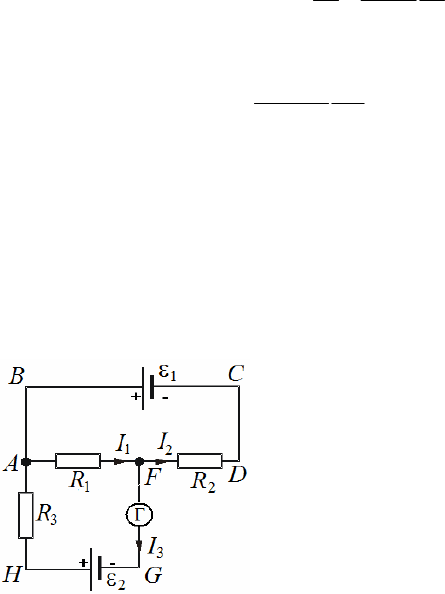
100
Разность потенциалов между точками А и В при отключенном
вольтметре равна произведению силы тока I
2
на половину сопро-
тивления потенциометра:
22
ε
22
пп
п
R
R
UI
Rr
==
+
.
Подставляя в эту формулу числовые значения, получим
2
B.
U ==
+
150 100
50
100 50 2
№ 5.
Электрическая цепь состоит из двух гальванических
элементов, трех сопротивлений и гальванометра. В этой цепи
R
1
= 100 Ом, R
2
= 50 Ом, R
3
= 20 Ом, ЭДС элемента ε
1
= 2 В. Гальва-
нометр регистрирует ток I
3
= 50 мА, идущий в направлении, ука-
занном стрелкой. Определить ЭДС ε
2
второго элемента. Сопро-
тивлением гальванометра и внутренним сопротивлением элемен-
тов пренебречь.
Р е ш е н и е.
Выберем направления токов, как
они показаны на рисунке, и условимся
обходить контуры по часовой стрелке.
По первому правилу Кирхгофа для
узла F имеем
I
1
– I
2
– I
3
= 0. (1)
По второму правилу Кирхгофа
имеем для контура АВСDFА:
–I
1
R
1
– I
2
R
2
= –ε
1
или, после умножения обеих частей равенства на –1,
I
1
R
1
+ I
2
R
2
= ε
1
. (2)
Соответственно, для контура AFGHA:
I
1
R
1
+ I
3
R
3
= ε
2
. (3)
После подстановки числовых значений в формулы (1), (2) и (3)
получим:
