Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

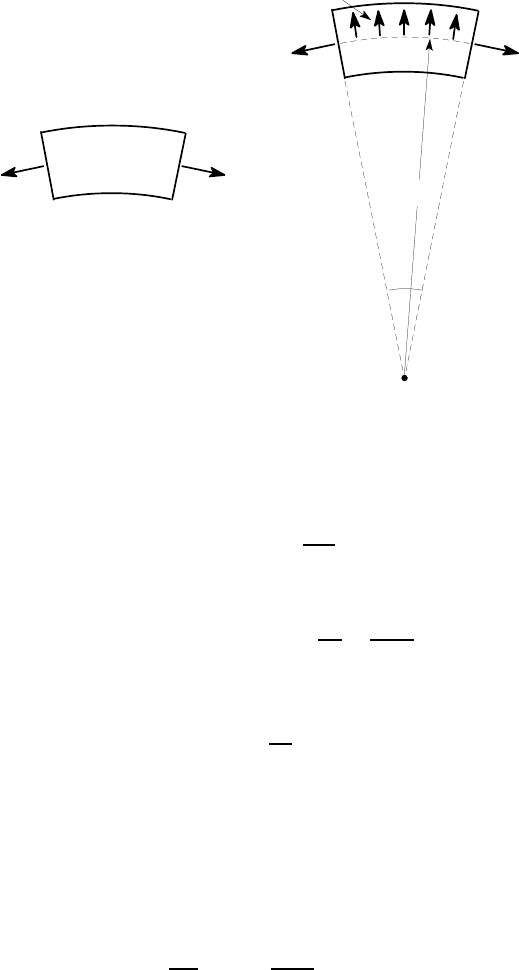
11.1 The governing equation 495

δθ

w per unit length

(a) (b)

Figure 11.6

Neglecting Poisson’s ratio effects from the stress components

, we then

have

θθ

= Ee

θθ

(11.18)

corresponding to an axial force

F =

θθ

dA = Eu

EAu

ˆr

, (11.19)

using (11.7). Eliminating u

between equations (11.18, 11.19) gives

θθ

F ˆr

. (11.20)

We can ﬁnd the line of action of the force F by taking moments about the axis of

curvature O. We ﬁnd

θθ

rdA = Eu

dA = EAu

It follows that the force passes through a point a distance

= EAu

ˆr

EAu

= ˆr

from O. In other words, the force for this simple mode of deformation passes through

the neutral surface of the bending analysis.

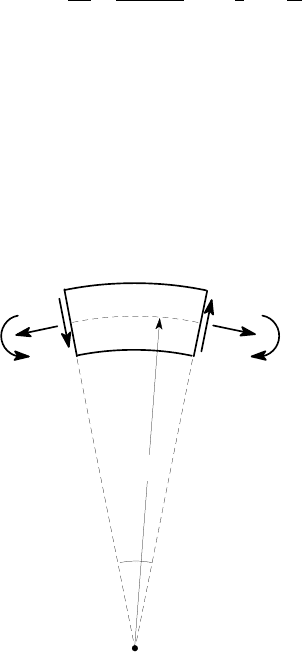
496 11 Curved Beams

This represents the most natural decomposition of the load into a force and a mo-

ment, since the force then produces no rotation of transverse planes and the moment

causes no extension of the ﬁbre located at the line of action of the force. However,

simpler expressions are obtained if we consider the stress ﬁeld due to a force whose

line of action passes through the centroid (r = ¯r) of the section. This loading can be

regarded as the superposition of a force F acting through r= ˆr and a bending moment

M = F(¯r−ˆr). The resulting stress ﬁeld is then

θθ

F ˆr

F(¯r − ˆr)

A(¯r − ˆr)



1 −

ˆr



. (11.21)

Thus, if the line of action of the force passes through the centroid, the stress

distribution is uniform and equal to F/A as in the elementary bending theory, but the

deformation will then involve a non-zero value of d

More general loading

If there is an axial force, but no radial load, the bending moment and the transverse

shear force in the beam must vary along the beam. The corresponding beam segment

is shown in Figure 11.7.

δθ

F+δF

V+δV

M+δM

Figure 11.7

Resolving forces in horizontal and vertical directions and taking moments about

the centre of curvature O, we obtain the three equilibrium equations

F +V

δθ

= 0 ;

V −F

δθ

= 0 ; R

F +

M = 0

and hence, in the limit

δθ

→0,

11.1 The governing equation 497

= −V ;

= F ;

= R

= −RV . (11.22)

The ﬁrst two equations can be combined to yield

+ F = 0 ;

+V = 0 (11.23)

and hence the most general solution for F,V, M in the absence of distributed loads is

F = A cos

+Bsin

; V = A sin

−Bcos

; M = ARcos

+BRsin

+C, (11.24)

where A,B,C are three constants to be determined from the end loading conditions.

The shear force V will generally cause initially plane transverse sections to de-

form out of plane and hence the preceding analysis is strictly not appropriate to this

case. However, as with straight beams, the stresses associated with the shear force

are generally fairly small and the simpler results can be used for general loading

without much loss in accuracy.

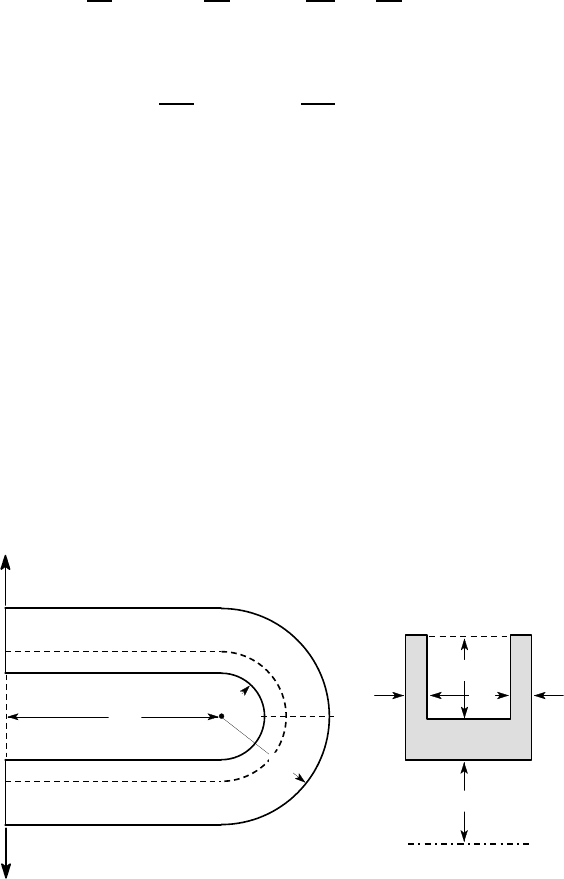
Example 11.2

Figure 11.8 shows a U-shaped curved beam with a symmetric channel cross section,

loaded by two opposed forces of magnitude 2kN. Find the neutral radius ˆr associated

with this cross section and the maximum tensile stress at the section A−A.

2 kN

100

5 5

Section A-A

all dimensions in mm

Figure 11.8

The cross section is conveniently regarded as the difference between the solid

(30×30) square and the dotted (20×20) square in Figure 11.9.

498 11 Curved Beams

all dimensions in mm

Figure 11.9

For the 30 ×30 square, (A

), we have

= 900 mm

, a = 20 mm, b = 50 mm, ¯r

a + b

= 35 mm, t = 30 mm

and

= t ln(b/a) = 27.4887 mm,

from (11.8).

For the 20 ×20 square (A

= −400 mm

, a = 30 mm, b = 50 mm, ¯r

= 40 mm, t = 20 mm

and

= −10.2165 mm.

These results are conveniently tabulated as in §4.3 as

i 1 2

900 –400

¯r

35 40

27.4887 –10.2165

We then have

A = A

+ A

= 900 −400 = 500 mm

A¯r = 900 ×35 −400 ×30 = 15500 mm

¯r =

15500

500

= 31 mm

= 27.4887 −10.2165 = 17.2722 mm.

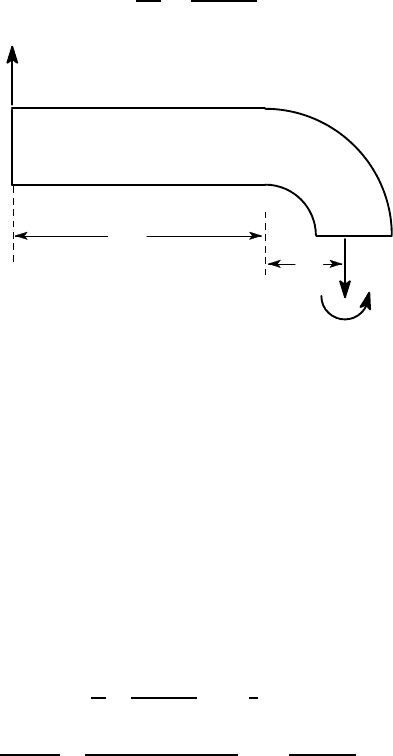
11.2 Radial stresses 499

and the neutral radius, ˆr is therefore

ˆr = A



500

17.2722

= 28.9483 mm.

2 kN

100

all dimensions in mm

Figure 11.10

Figure 11.10 shows a free-body diagram of the beam sectioned at A−A, at which

there will be an axial force F =2 kN and a bending moment, referred to the centroidal

radius ¯r = 31 mm of

M = 2(100 + 31) = 262 Nm (kNmm).

The direction of the bending moment in Figure 11.10 is opposite to that in Figure

11.1 (a), so we must take M = −262 Nm in equation (11.13). Also, it is clear from

Figure 11.7 that the maximum tensile stress will occur at the inner radius, r=20 mm

and its magnitude is

max

θθ

(20) =

A(¯r − ˆr)



1 −

ˆr



2 ×10

500

−262 ×10

500(31 −28.9483)



1 −

28.9483



= 118.3 MPa.

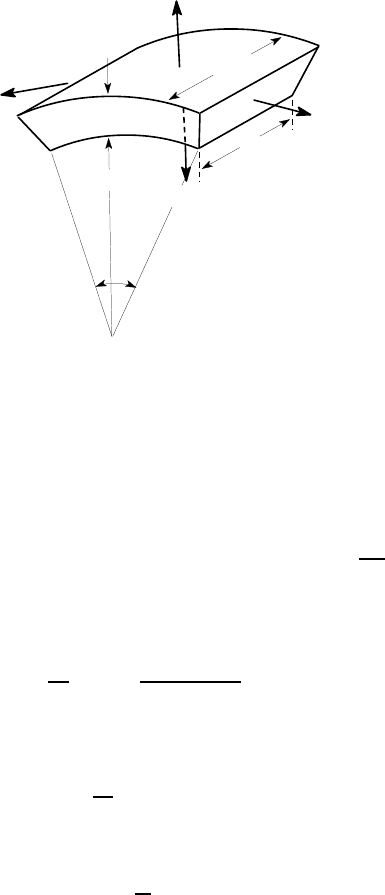
11.2 Radial stresses

In developing equation (11.5), we assumed that

θθ

was the only stress and in par-

ticular that the radial stress

was negligible. In practice, signiﬁcant radial stresses

can be developed in curved beams, but since their contribution to equation (11.5) is

multiplied by Poisson’s ratio which is fairly small, the above analysis generally gives

a good approximation to the circumferential stresses in the beam.

500 11 Curved Beams

θθ

σ t δr

θθ

σ t δr

σ tr δθ

t+δt

δθ

δr

rrrr

(σ +δσ )(t+δt)(r+δr)δθ

Figure 11.11: Radial equilibrium of a small beam element

We can estimate the distribution of radial stress by using an equilibrium argu-

ment. We ﬁrst need to modify the equilibrium equation (10.4) to include the effect

of a variable thickness in the axial direction. Figure 11.11 shows the small element

of the beam contained between the radial surfaces r and r +

r. The equilibrium

equation for this element, analogous to equation (10.1) with no acceleration term, is

(

δσ

)(r +

r)(t +

δθ

−

δθ

−2

θθ

r sin



δθ



= 0 .

Dividing throughout by r

δθ

and proceeding to the limit as

δθ

→0, we obtain

the differential equation of equilibrium

) +

(

−

θθ

= 0 , (11.25)

which clearly reduces to (10.4) if t is independent of r.

Equation (11.25) can be expressed in the form

(tr

) = t

θθ

The radial stress must be zero at the inner radius r = a and hence we can integrate

this relation to obtain

θθ

dr , (11.26)

which permits

to be determined, once

θθ

is known.

Example 11.3

Find the maximum radial stress

for the square section curved beam of Example

11.1.

11.2 Radial stresses 501

We already found the radii ˆr, ¯r for this beam in Example 11.1 above as

ˆr = 2.46630 in ; ¯r = 2.5 in

and hence the general expression for

θθ

(r) =

A(¯r − ˆr)



1 −

ˆr



100 ×12

1(2.5 −2.46630)



1 −

2.46630



= 35608 −

87821

psi,

where r is in inches.

For this geometry, t is constant and equal to 1 in, so substituting for

θθ

into

equation (11.26), we obtain



35608 −

87821



dr = 35608



1 −



−

87821

ln(r/2) .

θθ

r (in)

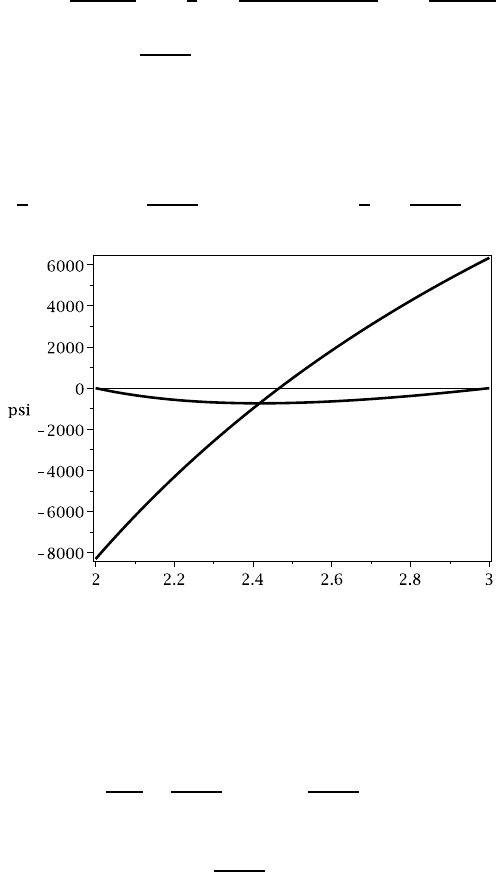
Figure 11.12: Stress distribution in the square section beam

The stresses

θθ

are shown as functions of r in Figure 11.12. The radial

stress is zero at the inner and outer radii, as required by the traction-free boundary

condition, and the maximum value occurs when

87821

ln(r/2) −

16605

= 0

and hence

r = 2exp



16605

87821



= 2.416 in.

The maximum radial stress is therefore

502 11 Curved Beams

max

= 35608



1 −

2.416



−

87821

2.416

ln(2.416/2) = −738 psi (compressive).

This is small compared with the maximum circumferential stress (6335 psi tensile at

r =3 and 8302 psi compressive at r =2) and can generally be neglected. However, it

is more signiﬁcant for severely curved beams (a/b ≪1) or for beams with a reduced

thickness t near the neutral surface.

The radial stress must necessarily be zero at the inner and outer radii and reach

a maximum somewhere near the mean radius. The derivative d

/dr in that region

is generally fairly small, so for a quick estimate of the magnitude of the maximum

radial stress, it is often sufﬁciently accurate to evaluate it at the neutral or centroidal

radii instead of calculating the exact maximum location. In the present example, we

have

(¯r) = 35608



1 −

2.5



−

87821

2.5

ln(2.5/2) = 717 psi,

whilst

(ˆr) = 35608



1 −

2.4663



−

87821

2.4663

ln(2.4663/2) = 730 psi,

both of which are sufﬁciently close to the actual maximum of 738 psi.

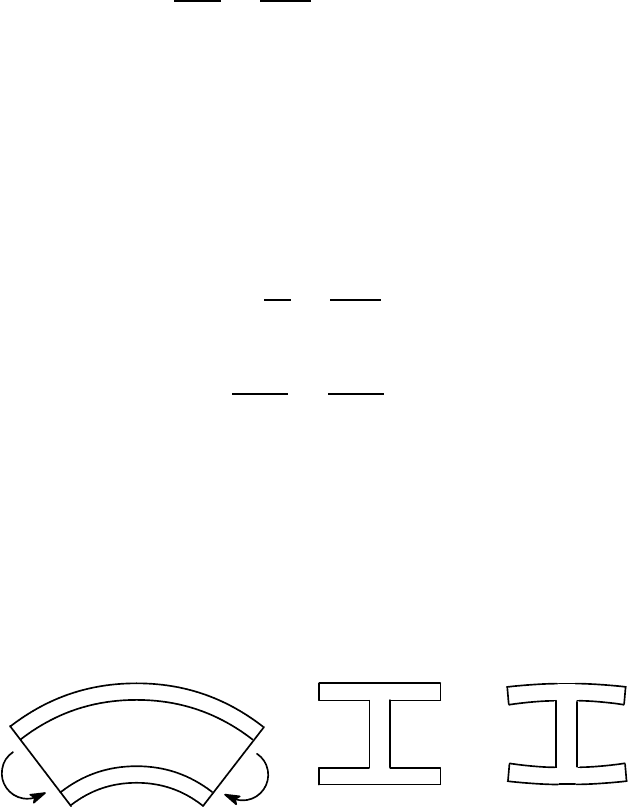
11.3 Dis tortio n of the cross section

The analysis in this chapter is based on the assumption that the cross section of the

beam remains undistorted during bending deformation. Unfortunately, this is a non-

conservative approximation and it can lead to serious errors for thin-walled cross

sections, such as I-beams and thin-walled cylinders (pipe bends), where the stiffness

is overestimated and the maximum stress underestimated.

(a) (b) (c)

Figure 11.13: Distortion of the cross section for a curved beam of I-section

To understand the mechanism of section distortion during bending, it is help-

ful to consider the strain energy associated with the assumed deformation. Figure

11.13 (a) shows a curved beam whose thin-walled I-beam cross section is shown in

Figure 11.13 (b). If the beam is subjected to a bending moment M, the outer ﬂange

will be loaded in tension, whilst the inner ﬂange is loaded in compression. Now sup-

pose that the beam ﬂanges were to distort, as shown in Figure 11.13 (c), the tips of

11.3 Distortion of the cross section 503

the outer ﬂange A bending inwards and those of the inner ﬂange B bending outwards.

As a result of this deformation, the ﬁnal radius of regions A will be reduced, so that

the tensile stress is reduced, resulting in a decrease in the strain energy U stored in

the beam. A similar effect is predicted for the outward motion of the inner ﬂanges

at B. Of course, there will be additional strain energy associated with the curvature

of the ﬂanges in Figure 11.13 (c), but for a sufﬁciently thin ﬂange, this will be small

and the net effect of the distortion will be a reduction of total strain energy. The sta-

tionary potential energy theorem (§3.5) therefore tells us to expect the beam section

to deform during bending as shown in Figure 11.13 (c). If the bending moment is

reversed in direction, the distortion is also reversed — i.e. the ﬂanges A will bend

radially outwards and the ﬂanges B will bend inwards.

This effect is clearly non-conservative, since by reducing the magnitude of

θθ

at A and B, the distortion reduces the corresponding bending moment. If the bend-

ing moment is prescribed, additional curvature change (

∆κ

) will occur, leading to

increased bending stresses at the middle of the ﬂanges, where radial motion is re-

strained by the web.

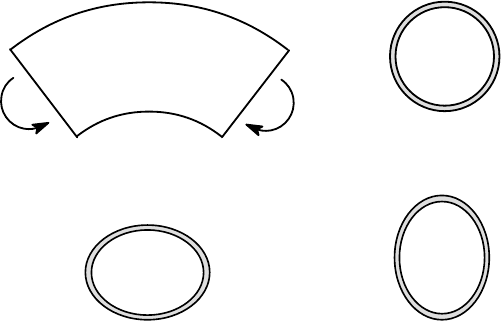
For thin-walled circular tubes (pipe bends), the same effect causes the section to

become oval during bending, as shown in Figure 11.14. The direction of ovalization

depends on the direction of the applied moment.

(a) (b)

Figure 11.14: (a) Curved thin-walled tube loaded in bending, (b) undeformed cross

section, (c) deformed cross section for positive M, (d) deformed cross section for

negative M

The most straightforward way to estimate the distortion of a thin-walled cross

section and its effect on the maximum stress is to approximate the expected deformed

shape by an appropriate function and use the Rayleigh-Ritz method (§3.6 above).

More details of this procedure can be found in Cook and Young (1985), §§10.5,

10.6.

504 11 Curved Beams

11.4 Range of a pplicatio n of the theory

The analysis of curved beams is somewhat more complicated than that for straight

beams and hence it makes sense to use the simpler theory if the radius of curvature

is large compared with the radial thickness of the beam. A comparison of the two

theories for a beam of rectangular cross section shows that the error involved in using

the elementary theory is less than 10% as long as b/a < 1.3, where a,b are the inner

and outer radii respectively, as shown in Figure 11.3. Another way of expressing this

condition is that the radial thickness of the beam (b−a) should be less than 30% of

the inner radius.

The elementary theory is much more successful in predicting the deﬂections in a

curved beam, particularly if the neutral radius ˆr is used to deﬁne the ‘length’ of the

beam (see Problem 11.3). For example, the error in the predicted stiffness of a beam

of rectangular cross section, compared with the curved beam result, is less than 10%

for b/a <14.

The curved beam theory is itself approximate, since equation (11.3) assumes that

the radial displacement u

is independent of r and we showed in §11.2 that the radial

stress

(and hence the strain e

) is non-zero. Fortunately, an exact solution to the

bending problem can be obtained for the rectangular cross section

and a comparison

with the curved beam theory

shows that the latter predicts a maximum stress within

10% of the exact value as long as b/a <11.

We conclude that the curved beam theory is useful in the range 1.3 < b/a < 11.

However, in a design problem, it is usually sensible to use the elementary theory

ﬁrst to obtain an estimate of the maximum stress even in this range. If the result is

very low relative to the allowable stress

all

(e.g. if

max

all

< 0.2), the extra effort

involved in a curved beam calculation is not justiﬁed.

11.5 Summary

In this chapter, we have shown that the stress distribution in a curved beam due to

a bending moment differs from that in a straight beam of similar cross section, and

the neutral surface is displaced towards the axis of curvature. The inner radius of the

beam acts as a stress concentration, causing an increase in the local bending stress.

Radial stresses as well as circumferential stresses are obtained and thin-walled

cross sections may experience signiﬁcant distortion.

The elementary bending theory gives a good estimate of the maximum stresses

and the deformation except when the radius of curvature of the beam is comparable

with the cross-sectional dimensions.

J.R. Barber (2010), Elasticity, Springer, Dordrecht, Netherlands, 3rd edn., Chapter 10.

R.D. Cook and W.C. Young (1985), Advanced Mechanics of Materials, Macmillan, New

York, §10.3.