Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

Problems 485

10.21*. An inﬁnite solid consists of an incompressible elastic-plastic material which

has modulus of rigidity G, and which yields at a shear stress

. The solid contains

a long cylindrical hole of radius b which contains ﬂuid at pressure p. Find the radial

and circumferential stresses in the solid for the case where p is sufﬁcient for yielding

to have progressed to a radius c.

Find the radial displacement at r = c and hence show that

= 1 + ln





∆



where V is the original volume of the hole and

∆

V is the change in its volume due to

the pressure p.

10.22. A thin steel annular disk of internal radius 2 in and external radius 8 in is

subjected to internal pressure at the inner radius, the outer edge being traction-free.

Obtain expressions for the stresses in the disk when the pressure p is sufﬁciently large

for there to be a plastic zone of outer radius c. The appropriate material properties

are E =30×10

psi,

=0.3,S

= 100×10

psi.

Show that the maximum value of p that can be applied is p = S

and that in this

condition, part of the disk remains in the elastic state. Describe the resulting failure

in physical terms.

10.23. A pressure vessel in the form of a long circular cylinder with closed ends is

subjected to an external pressure p. The internal radius of the cylinder is a and the

external radius is 2a. Show that if yielding is governed by the Tresca criterion and if

the value of p is large enough, yielding occurs up to a radius c given by





− p +



1 −



= 0 ,

where S

is the tensile yield stress of the material.

Sketch the distribution of radial and circumferential stress through the cylinder

wall for the case where c = 1.2a.

10.24. A rigid cylindrical container of radius a is sealed when it is just full of water

of density

at pressure p

. It is then rotated about its axis at speed

Ω

. Treating water

as an elastic-plastic material which yields at zero shear stress, but which has a bulk

modulus K, ﬁnd the pressure distribution in the water. Neglect gravitational effects.

At what speed would you expect your solution to cease to be valid?

Note: The bulk modulus is deﬁned such that

e ≡e

+ e

θθ

+ e

= −

where p is the hydrostatic pressure.

486 10 Thick-walled Cylinders and Disks

10.25. A long solid cylinder of radius a is rapidly heated around its curved surface

producing an instantaneous temperature distribution

T = T

+ T

If T

is large enough for some yielding to occur, ﬁnd the radius of the elastic region

and the instantaneous stress distribution in the cylinder. Assume that the material

obeys Tresca’s yield criterion and that the tensile yield stress S

is independent of

temperature.

10.26. A long circular cylinder of inside radius a and outside radius na has closed

ends. The material may be assumed to be elastic-perfectly plastic, obeying Tresca’s

yield criterion, with a yield stress S

in uniaxial tension. An external pressure just

sufﬁcient to cause yielding throughout the cylinder is applied and then removed. Find

the distribution of residual stress and hence the maximum value of n if there is to be

no yielding on unloading.

10.27. A cylindrical pressure vessel of inside radius a, outside radius 2a and closed

ends is subjected to an internal pressure p. Show that yield will occur throughout the

vessel if p =S

ln2.

If this pressure is applied and then released, show that the residual circumferen-

tial stress at the inner radius is

−



8ln2

−1



Curved Beams

The classical theory of the bending of beams is strictly exact if the axis of the beam

is straight, the loads are applied only at the ends and the cross section is uniform

along the length, which is much larger than any other linear dimension. However,

the resulting equations are so simple that engineers routinely apply them outside

this restrictive context and this usage is appropriate as long as we recognize that the

resulting approximation may underestimate the bending stresses.

A particular case in which this occurs is that where the axis of the beam is curved.

Important practical applications include chain links, crane hooks, pipe bends and

curved segments of machine tool frames.

11.1 The governing equation

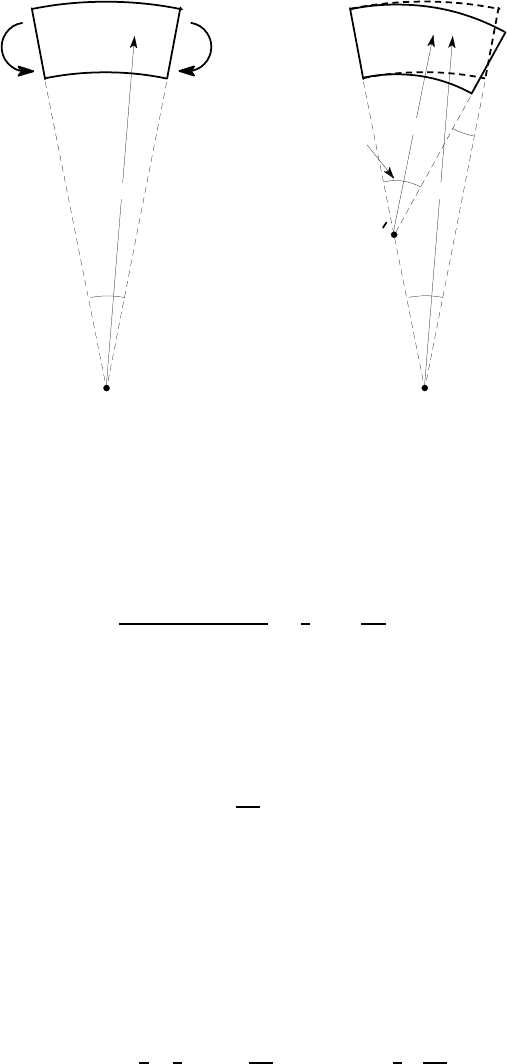
Figure 11.1 (a) shows a segment of a curved beam subtending a small angle

δθ

at its centre of curvature O and transmitting a bending moment M. The resulting

deformation is illustrated in Figure 11.1 (b), where the reference frame has been

chosen so as to leave the left end of the segment ﬁxed.

As in the elementary analysis of straight beams, a convenient starting point is the

assumption

that plane transverse sections remain plane during the deformation. The

right end of the segment will rotate through some angle

δφ

. This in turn causes the

subtended angle in the deformed segment to increase to

δθ

δφ

and the centre of

curvature to move to O

′

as shown.

As in §5.1, we can establish a more rigorous starting point by remarking that transverse

plane sections must all deform to the same shape, but will in general suffer different rigid

body translation and rotation. However, if the material is isotropic, it follows from symme-

try that plane sections remain plane.

J.R. Barber, Intermediate Mechanics of Materials, Solid Mechanics and Its Applications 175,

2nd ed., DOI 10.1007/978-94-007-0295-0_11, © Springer Science+Business Media B.V. 2011

488 11 Curved Beams

δθ

δθ+δφ

δφ

(a) (b)

Figure 11.1: (a) Curved beam loaded by a bending moment M; (b) the resulting

deformation

We denote the radius of a given point as r in the undeformed state and s in the

deformed state. The circumferential strain can therefore be written

θθ

δθ

δφ

) −r

δθ

→



1 +



−1 (11.1)

in the limit where

δθ

→ 0.

We anticipate the existence of a neutral surface at some radius r = ˆr at which

the circumferential strain is zero. The corresponding radius ˆs after deformation is

therefore (by deﬁnition) given by

ˆs



1 +



= ˆr . (11.2)

From the geometry of Figure 11.1 (b), the distance OO

′

d = r −s = ˆr − ˆs

and hence

s = r −d = r − ˆr + ˆs . (11.3)

The strain (11.1) can therefore be written

θθ



1 −

ˆr

ˆs



1 +



−1 =



1 −

ˆr



, (11.4)

11.1 The governing equation 489

using (11.2).

If the stress components

can be assumed to be negligible, we then have

θθ

= Ee

θθ

= E



1 −

ˆr



. (11.5)

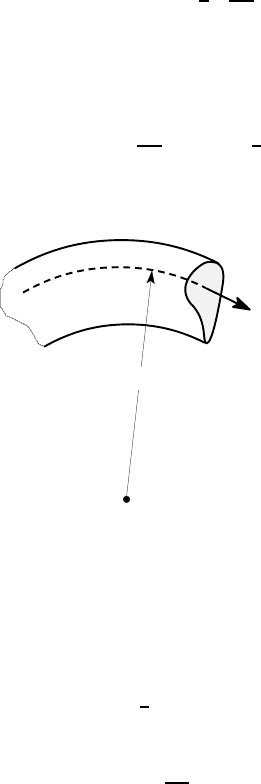
This stress acts on the cross section of the beam in the circumferential direction, as

shown in Figure 11.2 and it follows that the total circumferential force is

F =

θθ

dA = E



1 −

ˆr



dA , (11.6)

where the integral is performed over the cross-sectional area A of the beam.

θθ

Figure 11.2: The circumferential stress,

θθ

As with straight beams, it is convenient to treat circumferential (axial) load-

ing and bending separately and then superpose the resulting stress distributions. We

therefore focus initially on the case where the circumferential force is zero, in which

case



1 −

ˆr



dA = 0

and hence

A = ˆr

, (11.7)

which serves to determine the radius ˆr deﬁning the location of the neutral surface.

11.1.1 Rectangular and circular cross sections

Figure 11.3 (a) shows a curved beam of rectangular cross section, with inner radius

a, outer radius b and thickness t.

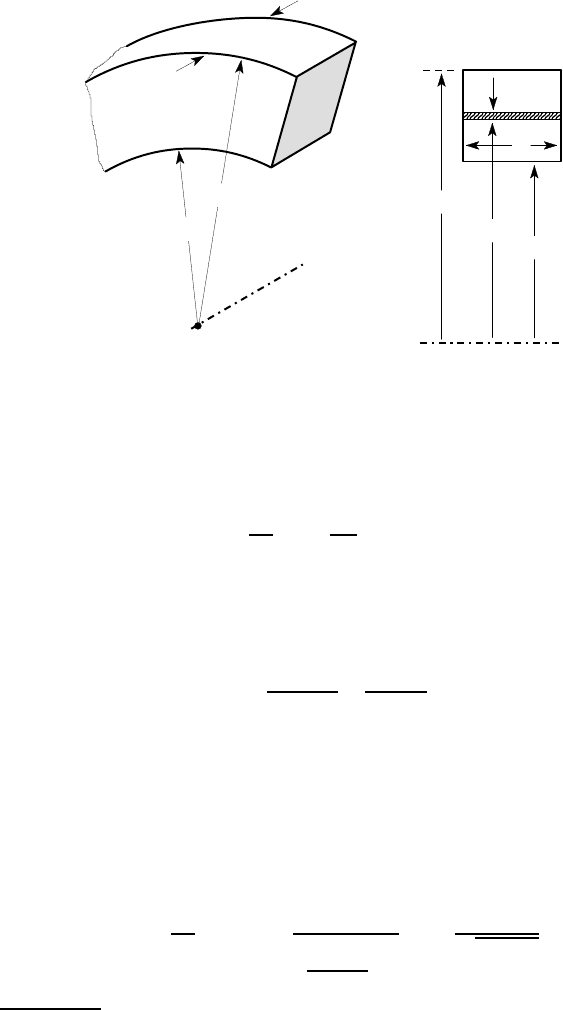
490 11 Curved Beams

(a) (b)

Figure 11.3: Curved beam of rectangular cross section

The integral in equation (11.7) for this cross section can be evaluated using the

rectangular elemental area dA =tdr shown shaded in Figure 11.3 (b).

We then have

tdr

= t ln(b/a) . (11.8)

The cross-sectional area is

A = (b −a)t

and hence the neutral radius ˆr is given by

ˆr =

(b −a)t

t ln(b/a)

(b −a)

ln(b/a)

. (11.9)

If the beam is only slightly curved, so that a,b≫(b−a) and b/a is close to unity,

it can be shown that ˆr →(a+b)/2. In other words, the neutral surface approaches the

mid-plane of the section as in the elementary theory.

Figure 11.4 (a) shows a curved beam of circular cross section of radius a, whose

axis deﬁnes an arc of radius R. To evaluate the integral in equation (11.7), we use the

shaded elemental area of Figure 11.4 (b), obtaining

(R +

cos

)

πρ

−

= 2

(R −

−a

) . (11.10)

see for example I.S. Gradshteyn and I.M. Ryzhik (1980), Tables of Integrals, Series and

Products, Academic Press, New York, 3.613.

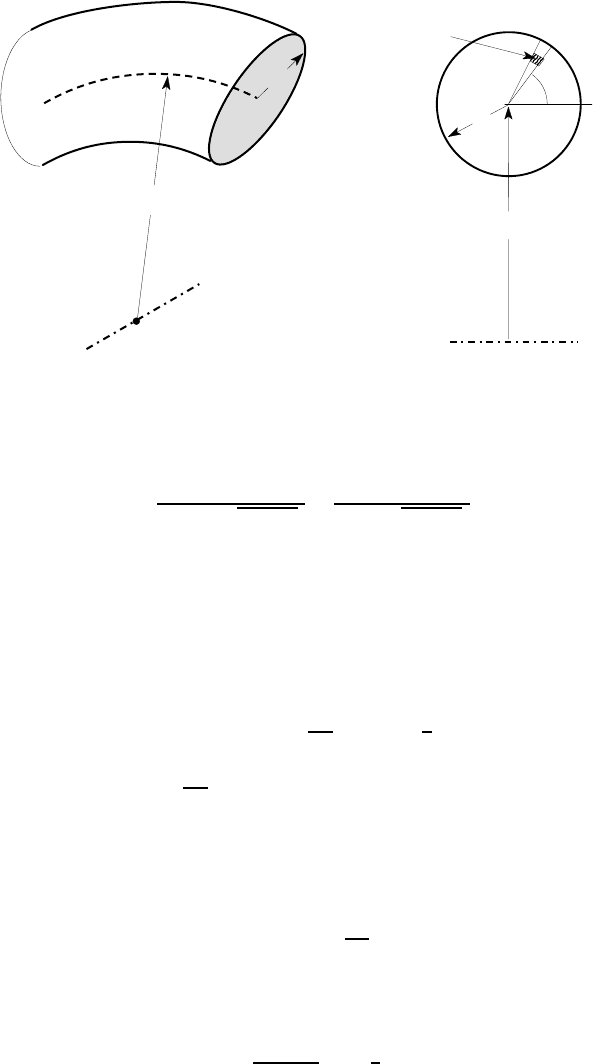
11.1 The governing equation 491

ρδρδθ

(a) (b)

Figure 11.4: Curved beam of circular cross section

The cross-sectional area of the circle is

and the neutral radius is therefore

ˆr =

(R −

√

−a

)

2(R −

√

−a

)

, (11.11)

from (11.7).

11.1.2 The bending moment

Referring back to Figures 11.1, 11.2, we can develop an expression for the bending

moment M by taking moments about the curvature axis O. We obtain

M =

θθ

rdA = E



1 −

ˆr



rdA

= E



rdA −

ˆrdA



using (11.5).

The ﬁrst integral is equal to A¯r, where ¯r is the distance from O to the centroid of

A, so the moment expression can be written in the condensed form

M = EA(¯r − ˆr)

. (11.12)

The stress due to the bending moment M can then be obtained by eliminating

between equations (11.5, 11.12), with the result

θθ

A(¯r − ˆr)



1 −

ˆr



. (11.13)

492 11 Curved Beams

The deformation caused by the moment can be characterized by the derivative

EA(¯r − ˆr)

. (11.14)

Alternatively, we note that the change of curvature,

∆κ

of the neutral surface is

deﬁned by

∆κ

≡

ˆs

−

ˆr

EAˆr(¯r − ˆr)

, (11.15)

from equations (11.2, 11.14).

As in Chapter 3 (§3.2), we can compute the strain energy stored in the beam

segment

δθ

by equating it to the work done by the moment M during its application.

We obtain

U =

δφ

δθ

2EA(¯r − ˆr)

from (11.14) and hence

2EA(¯r − ˆr)

. (11.16)

This result permits us to use the energy methods of Chapter 3 in curved beam prob-

lems (see for example Problems 11.10, 11.11).

Equations (11.12–11.16) contain the factor (¯r−ˆr), which is often small in com-

parison with ¯r. It is important to take a sufﬁcient number of signiﬁcant digits in the

calculation of these quantities to ensure that accuracy is not lost. This will be clariﬁed

by the following example.

Example 11.1

A curved beam of 1 in square cross section and inner radius 2 in subtends an angle

of 90

at the centre, as shown in Figure 11.5. Find the stresses at the inner and outer

radii when the beam is subjected to a bending moment of 100 lb ft. Find also the

relative rotation of the ends of the beam, if the material is steel with E =30×10

psi.

100 lb ft

all dimensions in inches

Figure 11.5

11.1 The governing equation 493

The inner and outer radii are a=2 in, b =3 in, respectively, so the neutral radius

can be found from equation (11.9) as

ˆr =

(b −a)

ln(b/a)

ln(1.5)

= 2.46630 in.

The centroidal radius is

¯r = 2.5 in.

Notice that we have to take a larger number of signiﬁcant digits in ˆr, ¯r than usual

because the stress and deformation expressions involve the difference (¯r−ˆr) between

quantities of comparable magnitude.

The stress at the outer radius (b = 3 in) can now be found from equation (11.13)

θθ

(b) =

A(¯r − ˆr)



1 −

ˆr



100 ×12

1(2.5 −2.46630)



1 −

2.46630



= 6335 psi (tensile).

A similar calculation for the inner radius, a=2 in, yields

θθ

(a) =

100 ×12

1(2.5 −2.46630)



1 −

2.46630



= −8302 psi (compressive).

Notice that the magnitude of the stress at the inner radius exceeds that at the outer

radius. This is due to the stress concentrating effect of the curvature and is more

pronounced when the ratio a/b is smaller.

The deformation of the beam is deﬁned by equation (11.14), from which we

obtain

EA(¯r − ˆr)

100 ×12

30 ×10

×1(2.5 −2.46630)

= 1.187 ×10

−3

The relative rotation of the ends is therefore

δφ

= 1.187 ×10

−3

×90

= 0.107

It is instructive to compare the maximum stresses with the predictions of the

elementary bending theory for straight beams, which gives

max

100 ×12 ×0.5

/12

= 7200 psi.

The elementary theory predicts equal and opposite stresses at the inner and outer

radii, so it underestimates the stress at the inner radius and overestimates it at the

outer radius, in each case by about 14%.

494 11 Curved Beams

11.1.3 Composite cross sections

The preceding analysis applies to any cross section which is symmetric about a plane

normal to the curvature axis of the beam. For a general cross section, we must ﬁrst de-

termine the neutral radius ˆr from equation (11.7) and the centroidal radius ¯r using the

methods of §4.3. The circumferential stress distribution and the moment-curvature

relation are then given by equations (11.13–11.15).

For composite areas

A = A

+ A

+ ... ,

the integral in (11.7) can be written as the sum of a series of separate integrals, as in

§4.3. We obtain

ˆr

+ ... (11.17)

The results of §11.1.1 therefore permit us to write down the integral for any area

made up of rectangular and/or circular segments.

11.1.4 Axial loading

The analysis so far has been restricted to the case of pure bending, where the axial

force F deﬁned by equation (11.6) is zero. In this section, we shall consider the

opposite case, where there is an axial force, but no bending moment.

Figure 11.6 (a) shows a segment of curved beam loaded by an axial force F

on its ends. The segment is clearly not in equilibrium, since the two forces are not

co-linear, so we conclude that a curved beam cannot support a uniform axial load

along its length without additional loading. The simplest loading scenario leading

to a uniform axial force is that shown in Figure 11.6 (b), where the forces F are

balanced by a uniformly distributed radial load of w per unit length. If the subtended

angle

δθ

is sufﬁciently small, the equilibrium equation for this ﬁgure is

δθ

−2F

δθ

= 0

and hence

w =

This loading leads to an axisymmetric state of stress and deformation and is

in fact analogous to that in the membrane theory of axisymmetric shells (Chapter

8). The subtended angle

δθ

must remain the same after deformation and hence the

circumferential strain is

θθ

where u

is the radial displacement.

cf equation (8.3).