Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

12.1 Uniform beam in compression 515

Figure 12.4: The ball resting on (a) a horizontal surface (neutrally stable); (b) a

concave surface (stable) and (c) a convex surface (unstable)

The neutrally stable system of Figure 12.4 (a) is intermediate between those of

Figures 12.4 (b,c) and we should therefore not be surprised to ﬁnd that the neutrally

stable conﬁguration of Figure 12.3 (b) is intermediate between domains of stability

and instability. In other words, if

L <

, the only solution (A =B = 0) of equations

(12.8, 12.9) is stable, whereas if

it is unstable. We shall prove this result using

an energy argument in §12.7.2 below.

The lowest critical force P

for neutral stability is deﬁned by

L =

(12.12)

and hence

. (12.13)

If P>P

the system is unstable, if P <P

it is stable and if P=P

it is neutrally stable.

The higher modes corresponding to

L= 2

, 3

, etc are unattainable unless the

system is somehow constrained to inhibit the lowest mode. This can be done by

adding a simple support at the mid-point z=L/2, since the solution

u = Bsin(2

z/L) , (12.14)

corresponding to

L=2

is zero at z=L/2, whereas that corresponding to

u = Bsin(

z/L) , (12.15)

which is non-zero everywhere except at the end supports. Thus, with a support at the

mid-point, the beam will ﬁrst buckle at the higher force

P =

, (12.16)

corresponding to

L=2

and the buckled shape will be of the form shown in Figure

12.5.

Figure 12.5: Second buckling mode for the simply supported beam

(a) (b) (c)

516 12 Elastic Stability

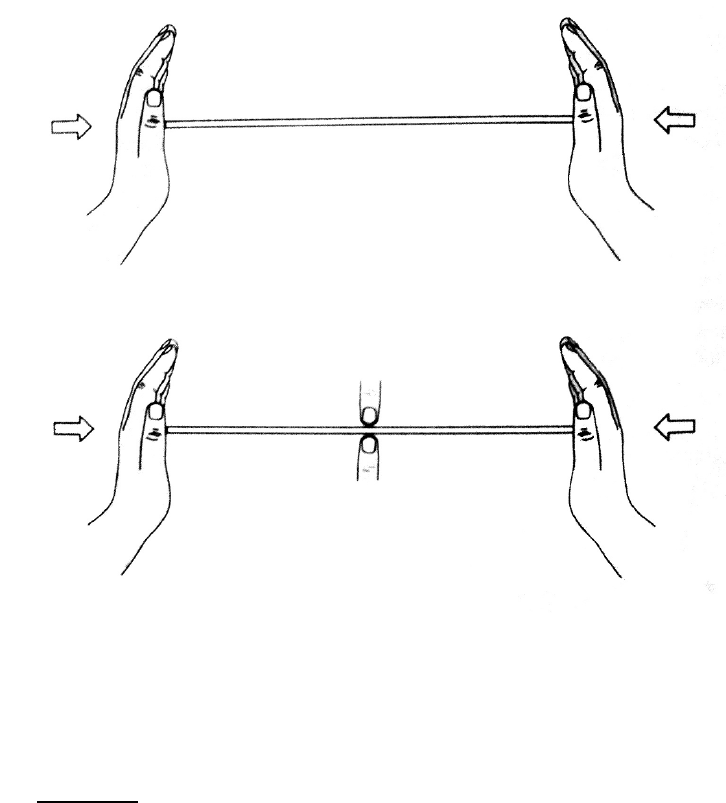
The reader is encouraged to conﬁrm these results by experiment. A thin plastic

ruler is suitable as an experimental beam. Alternatively, you can make one by cutting

a 1 inch ×10 inch strip of fairly substantial cardboard, such as the backing from a pad

of writing paper. Load the beam in compression between the two hands, taking care

not to restrain rotation of the ends, as shown in Figure 12.6 (a). Observe the lowest

buckling mode and retain a physical impression of the required buckling force. Now

get a friend

to restrain the mid-point of the beam by lightly pinching it between two

ﬁngers, as in Figure 12.6 (b).

(a)

(b)

Figure 12.6: Buckling experiment (a) the simply supported beam; (b) with a central

restraint

You should ﬁnd that a substantially larger force is now required to buckle the

beam and the buckling mode is a complete sine wave, as in Figure 12.5. You should

also discover that very little restraint is needed at the centre support to achieve this

result. In fact, if the beam and the supports are perfectly aligned, this reaction is

theoretically zero. From a design point of view, we might therefore expect to be

If you have no-one to help you, compress the beam by pushing it with one hand against a

rigid surface, so as to have a hand free for the central support.

12.2 Effect of initial perturbations 517

able to increase the load carrying capacity of compression members by providing

arbitrarily ﬂimsy intermediate supports. This is not strictly true and we shall return

to this issue in §12.5 below. However, it is true that design against elastic instability

is best achieved by the judicious placing of supports to suppress low order buckling

modes.

Equation (12.10) has a denumerably inﬁnite set of solutions

L = n

where n

is any positive integer. The deﬂected shape corresponding to these solutions will

cross the axis (n−1) times in the length of the beam and the nth mode can only be

generated if supports are placed at all these nodes.

The problem considered above is a classical eigenvalue problem. It deﬁnes a

problem through a homogeneous set of equations [in this case equations (12.3, 12.6,

12.7)], which are homogeneous since the right-hand sides are zero. These equations

have only a trivial (null) solution, except for certain eigenvalues of the force P. At

these eigenvalues, the solution has a form u(z) known as the eigenfunction, but any

linear multiple of this function is a solution, as is shown in this case by the fact that

the arbitrary constant B can take any value. It is typical of eigenfunctions that the

nth eigenfunction crosses zero (n−1) times. Also, eigenfunctions generally form an

orthogonal set. In the present case, they are Fourier terms, which are orthogonal to

each other.

12.2 Effect o f initial perturbations

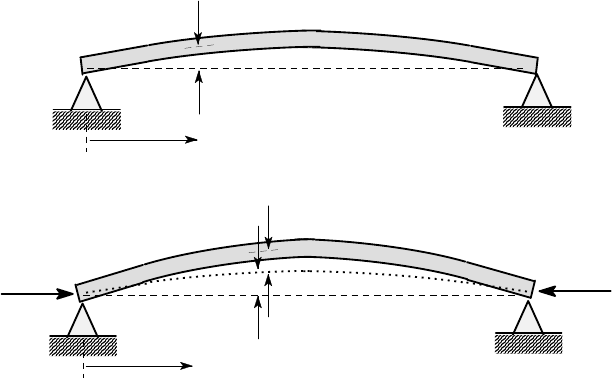
Suppose that the beam of Figure 12.2 (a) was not quite straight due to manufacturing

errors. We can describe this initial condition by stating that the beam has a deﬂection

(z) even before the compressive force is applied, as shown in Figure 12.7 (a).

(a)

u (z)

(b)

u (z)

u(z)

P P

Figure 12.7: Beam with initial perturbation (a) before loading, (b) after loading

518 12 Elastic Stability

We now apply a compressive force P causing an additional deﬂection u(z), as

shown in Figure 12.7 (b), so that the bending moment at any point is given by

M = P(u + u

) . (12.17)

The bending moment-curvature relation here involves only the additional deﬂection,

u(z), since no moment was needed to establish the state u

(z). It follows that M =

−EId

u/dz

and hence

= −

(z)

, (12.18)

from (12.17). Thus, the effect of the initial imperfection is to make the governing

differential equation inhomogeneous.

The general solution of equation (12.18) can be written as the sum of any partic-

ular solution and the general solution of the corresponding homogeneous equation.

If u

(z) is a polynomial, trigonometric or exponential function, a particular solution

can be determined by assuming u(z) to have the same general form and then equat-

ing coefﬁcients. The homogeneous equation corresponding to (12.18) is (12.3) and

hence the general homogeneous solution of (12.18) is given by (12.4). The general

solution will contain two arbitrary constants, which are determined from the kine-

matic boundary conditions.

Since the equation is inhomogeneous, some deﬂection is produced for all values

of the compressive force P, but we shall ﬁnd that it increases without limit as P

approaches the critical force P

of equation (12.13).

Example 12.1

The simply supported beam of Figure 12.7 has length L, ﬂexural rigidity EI and an

initial deﬂection deﬁned by

(z) =

z(L −z)

where

≪L. Find the deﬂected shape when the beam is compressed by a force P and

sketch the variation of the maximum deﬂection with P.

In this case, the differential equation (12.18) takes the form

= −

z(L −z)

EIL

and the right-hand side is a second degree polynomial, so we seek a particular integral

(z) of the same form, i.e.

(z) = C

z +C

where C

are as yet unknown constants.

Substituting u

(z) into the governing equation, we obtain

12.2 Effect of initial perturbations 519

z +C

) =

EIL

−zL) .

We now equate coefﬁcients of z

, obtaining

= 0 ;

= −

EIL

;

EIL

with solution

= −

; C

= −

; C

The general solution of the governing equation is then obtained by substituting

these results into u

(z) and superposing the general homogeneous solution (12.4),

with the result

u(z) =



−Lz −

2EI



+ A cos

z + Bsin

z .

The simply supported boundary conditions u(0) = u(L) = 0 then give the two

equations

−

+ A = 0



−L

−

2EI



+ A cos

L + Bsin

L = 0

for the unknown constants A,B, with solution

A =

; B =

(1 −cos

sin

and hence

u(z) =



−Lz −

2EI





cos

z +

(1 −cos

L)sin

sin



The deﬂected shape of the beam due to the compressive force P is therefore

deﬁned by

u(z) + u

(z) =



(1 −cos

L)sin

sin

−(1 −cos



In interpreting this expression, it is important to recognize that the applied

force P appears explicitly in the term 8

EI/PL

, but also implicitly in the terms

sin

z,cos

L, etc., since

P/EI, from (12.5).

The maximum displacement occurs at the mid-point z = L/2, and after some

algebra can be written

max

= u





+ u







sec





−1



sec

4EI

−1

520 12 Elastic Stability

This expression becomes unbounded as

→

and hence P →

= P

which is the same critical force determined for the homogeneous problem in equation

(12.13).

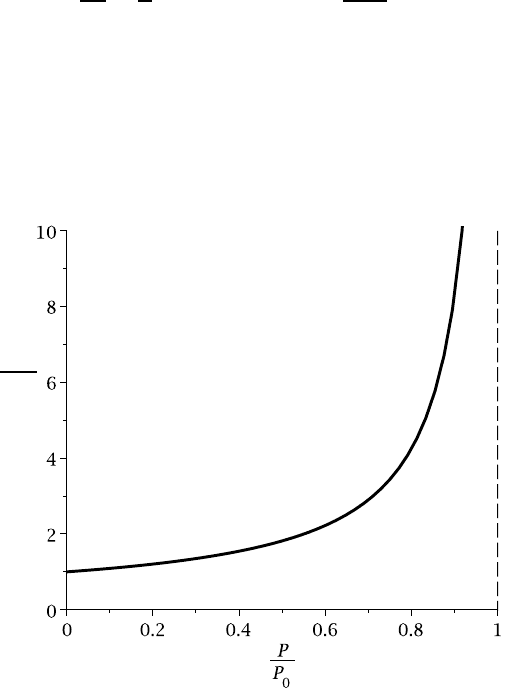
The maximum deﬂection is plotted as a function of the ratio P/P

in Figure 12.8.

The deﬂection is unbounded at P →P

, but substantial deﬂections are produced at

signiﬁcantly lower compressive forces. No manufacturing process is perfect, so it is

prudent to avoid column designs in which the maximum axial force exceeds 70% of

the theoretical critical force.

Figure 12.8: Central deﬂection as a function of compressive force

max

12.2.1 Eigenfunct ion expansions

In Example 12.1, the constant B →∞ as P →P

(

L →

), whilst the constant A re-

mains bounded. As a result, the expression for u(z) is increasingly dominated by the

term B sin

z as the critical force is approached, even though the initial perturbation

is not sinusoidal.

This is a general characteristic of eigenvalue problems. As the eigenvalue is ap-

proached, the response to any initial perturbation will grow without limit and the

shape of the resulting functions will approach that of the corresponding eigenfunc-

tion of the homogeneous problem.

12.3 Effect of lateral load (beam-columns) 521

This effect can be made more explicit by expanding the initial perturbation as an

eigenfunction expansion. In the present case, the eigenfunctions are of the sinusoidal

form sin

z, with

L= n

[see equations (12.4, 12.8, 12.11)] and hence we write

(z) =

∞

∑

n=1

sin





, (12.19)

where C

is a set of unknown coefﬁcients that can be determined by inverting the

Fourier series (12.19).

Substitution of (12.19) into (12.18) will now yield a differential equation whose

solution can be written in the form

u(z) =

∞

∑

n=1

sin





. (12.20)

The new coefﬁcients A

can be found in terms of the C

by equating coefﬁcients,

with the result

= C



−1



. (12.21)

Now clearly the A

will be of the same order as the C

except when the denomi-

nator of (12.21) is small compared with unity, which happens for the term A

when P

is close to P

. Thus, the deﬂection of the beam [equation (12.20)] will be dominated

by the ﬁrst eigenfunction when the ﬁrst critical force is approached, whatever form

is taken by the initial perturbation.

This technique of expressing the ‘forcing term’ (in this case the initial perturba-

tion) as an eigenfunction expansion is mathematically analogous to the expansion of

the response of a dynamic system in terms of normal modes. It depends on the fact

that the eigenfunctions are orthogonal and complete — i.e. that any arbitrary initial

beam shape can be expanded in such a series.

12.3 Effect o f lateral load (beam-columns)

Another class of inhomogeneous stability problems arises if an initially straight beam

is subjected to both axial and lateral loading. Beams loaded in this way are some-

times referred to as beam-columns, since they combine features of traditional beam

bending with axial loading as a column.

The lateral load will produce some lateral deﬂection even in the absence of the

axial force, but the latter exaggerates the deﬂection, causing it to go unbounded as

the critical axial force is approached. The axial force also exaggerates the bending

moment due to lateral loading and this effect can be important even when the axial

force is signiﬁcantly sub-critical. The deformed shape approaches more closely to

the theoretical eigenfunction for purely axial loading as the compressive axial force

is increased.

The analysis of beam-columns proceeds exactly as in the cases considered in

previous sections. We sketch a free-body diagram of the beam in an as yet unknown

522 12 Elastic Stability

deformed conﬁguration and determine the bending moment as a function of z from

equilibrium considerations, taking care to include the moment due to the axial force.

We then substitute the moment into the bending equation, solve the resulting ordinary

differential equation and determine the two arbitrary constants from the kinematic

boundary conditions.

Example 12.2

Figure 12.9 (a) shows a uniform cantilever beam of ﬂexural rigidity EI and length L,

loaded by an axial force P and a lateral force F at the free end. Find the maximum

bending moment in the beam and sketch its variation with P for a given value of F.

(a)

(b)

u(z)

u(L)

L - z

Figure 12.9: (a) Cantilever loaded by an axial force and a lateral force; (b) free-body

diagram for a beam segment

Figure 12.9 (b) shows the free body diagram for a segment of the beam of length

z at the loaded end. It is clear that the axial force and the shear force at the cut must

be P and F, respectively, and taking moments about the cut we have

M = −P [u

−u(z)] −F(L −z) ,

where u

= u(L) is the displacement at the end z = L. Notice in particular that the

moment arm for the force P [the perpendicular distance between the two equal and

opposite forces P in Figure 12.9 (b)] is [u

−u(z)], rather than simply u(z) as in Ex-

ample 12.1. This is because the end is unsupported and therefore has a non-zero

deﬂection u

. Also, it is convenient to treat u

as a separate unknown at this stage,

only imposing the condition u

= u(L) when the boundary conditions are being ap-

plied.

The governing equation is

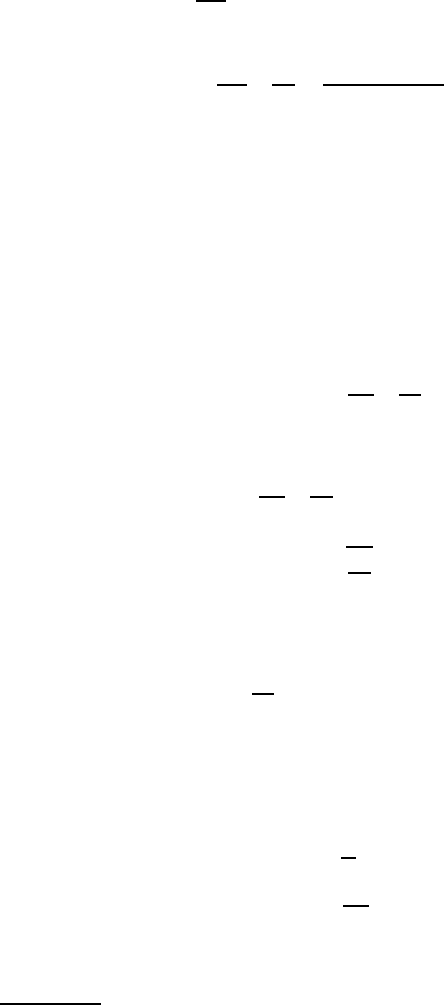
12.3 Effect of lateral load (beam-columns) 523

= −M = P [u

−u(z)] + F(L −z)

and hence

+ FL −Fz

Notice how this equation has the same form as the inhomogeneous equation (12.18),

only the right-hand side being different. In general, for any stability problem for

straight beams, the left-hand side of the governing equation [i.e. the terms containg

the unknown displacement function u(z)] will be identical to that in (12.18) and

hence the corresponding homogeneous equation will always be (12.3). This provides

a useful check on the sign convention. If you end up with (d

u/dz

−P/EI) as the

left-hand side, you have almost certainly

made a sign error and would do well to

check carefully before proceeding.

The right-hand side of the governing equation is a ﬁrst order polynomial in z and

elementary calculations show that a suitable particular solution is

(z) = u

−

The general solution is obtained by superposing the homogeneous solution (12.4)

and is

u(z) = u

−

+ A cos

z + Bsin

z ,

where

In this case, there are three unknowns A,B,u

, which can be determined from the

two kinematic boundary conditions

= u = 0 ; z = 0

and the deﬁnition

u = u

; z = L .

Substituting for u(z), we obtain the three simultaneous algebraic equations

−

+ B

= 0

+ A = 0

+ A cos

L + Bsin

L = u

with solution

The exception is if the axial force is tensile instead of compressive. See for example, Prob-

lem 12.8.

524 12 Elastic Stability

A = −

tan

L ; B =

; u

tan

L −

Substituting these results into the expression for u(z), we obtain

u(z) =

F tan

(1 −cos

z) −

(

z −sin

z) .

The ﬁrst term in this expression increases without limit as

L→

/2, correspond-

ing to the critical force

The maximum bending moment ocurs at z = 0 and is

max

| = Pu

+ FL =

tan

L −FL + FL = F

tan

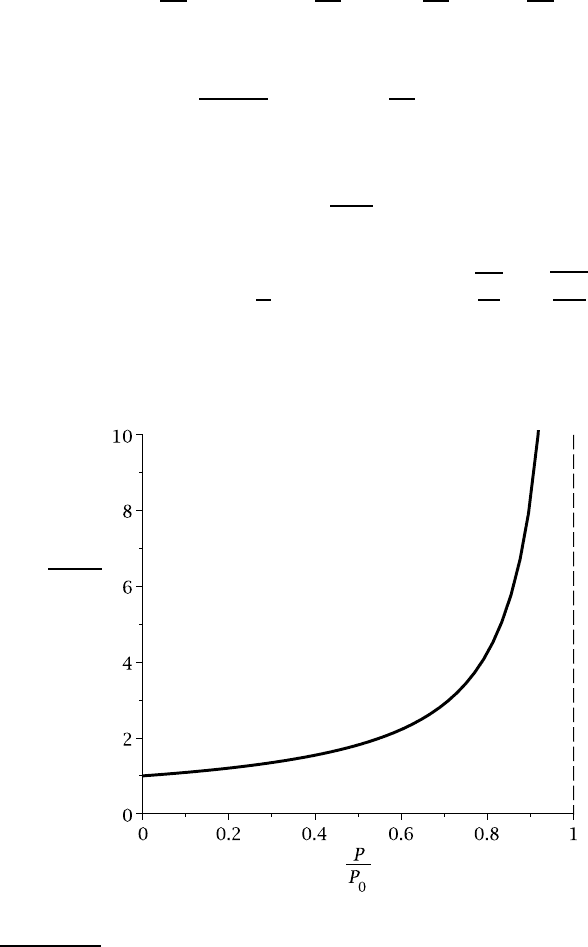
This is shown as a function of the dimensionless axial force P/P

in Figure 12.10.

Notice that the axial force causes a signiﬁcant increase in the maximum bending

moment for values as low as P=0.2P

Figure 12.10: Maximum bending moment as a function of axial compressive force

max

The perceptive reader may be puzzled by the fact that the expression for u(z) contains P

in the denominator and hence appears to be unbounded as P →0. However, in this limit,

also tends to zero and by replacing the trigonometric functions by the ﬁrst few terms

of their power series expansions, it can be shown that the solution does indeed tend to the

correct expression for a cantilever beam with an end load F, when P →0.