Barber J.R. Intermediate Mechanics of Materials
Подождите немного. Документ загружается.

10.2 The thin circular disk 455
Rewriting (10.18) with this result, we have
d
dr
1
r
d
dr
(ru
r
)
= −
ρΩ
2
(1 −
ν
2
)r
E
+
α
(1 +
ν
)
dT
dr
(10.19)
and hence, after integration,
1
r
d
dr
(ru
r
) = −
ρΩ
2
(1 −
ν
2
)r
2
2E
+
α
(1 +
ν
)T +C ,
where C is an arbitrary constant. Multiplying both sides of the equation by r and
integrating again yields
ru
r
= −
ρΩ
2
(1 −
ν
2
)r
4
8E
+
α
(1 +
ν
)
Z
Trdr +
Cr
2
2
+ D
and hence
u
r
= −
ρΩ
2
(1 −
ν
2
)r
3
8E
+
α
(1 +
ν
)
r
Z
Trdr +
Cr
2
+
D
r
. (10.20)
The stresses can then be recovered by substituting for u
r
in equations (10.16,
10.17). We obtain
σ
rr
= −
(3 +
ν
)
ρΩ
2
r
2
8
−
E
α
r
2
Z
rT dr + A +
B
r
2
(10.21)
σ
θθ
= −
(1 + 3
ν
)
ρΩ
2
r
2
8
+
E
α
r
2
Z
rT dr −E
α
T + A −
B
r
2
, (10.22)
where A,B are two new arbitrary constants related to C, D through
A =
EC
2(1 −
ν
)
; B = −
ED
(1 +
ν
)
,
which are introduced in order to avoid unnecessary algebraic complication in prob-
lems where only the stresses are required. The equivalent form of equation (10.20)
using the constants A,B is
u
r
= −
(1 −
ν
2
)
ρΩ
2
r
3
8E
+
α
(1 +
ν
)
r
Z
rT dr +
A(1 −
ν
)r
E
−
(1 +
ν
)B
Er
. (10.23)
Equations (10.21–10.23) define the general solution for the problem of the ax-
isymmetric circular disk. The temperature distribution T and the rotational speed
Ω
will generally be known and the constants of integration A,B are determined from
one condition at each of the inner and outer radii of the disk. If the disk is solid, there
is no inner radius, but a second equation for A,B is obtained from the condition that
the stresses must be bounded at the origin. We shall illustrate the solution procedure
in two examples.
456 10 Thick-walled Cylinders and Disks
Example 10.1 — Bursting speed of a grinding wheel
Figure 10.3 shows a grinding wheel of 150 mm inside diameter and 600 mm out-
side diameter. It is bonded to a cylindrical rigid shaft at the inside diameter and is
unloaded at the outside diameter. The wheel has an effective modulus E = 10 GPa,
ν
=0.3 and the density is 2500 kg/m
3
. Find the maximum safe rotational speed if the
maximum permissible tensile stress is 10 MPa. (The maximum permissible rotational
speed or the ‘bursting speed’ of a grinding wheel is specified by the manufacturer.)
150
600
Ω
all dimensions in mm
Figure 10.3: Grinding wheel
In this problem, the principal loading is that due to rotation. Additional stresses
may result from heating of the grinding wheel during operation, but we shall neglect
this effect (dropping out the terms involving temperature) in the following calcula-
tion.
The curved outer edge of the wheel, corresponding to r = 300 mm, is unloaded.
Referring back to Figure 10.1, we see that the stress component
σ
rr
acts on the curved
surface of the element
4
and hence we conclude that
σ
rr
= 0 at r = 300 mm. This
condition and equation (10.21) gives the equation
0 = −
3.3 ×2500 ×
Ω
2
×0.3
2
8
+ A +
B
0.3
2
.
A second equation is obtained from the fact that the wheel is bonded to a rigid
shaft at the inner edge r = 75 mm. This requires that the radial displacement of the
wheel u
r
be zero at r= 75 mm, since otherwise a gap would open between the wheel
and the shaft. Thus,
0 = −
0.91 ×2500 ×
Ω
2
×0.075
3
8 ×10 ×10
9
+
0.7 ×A ×0.075
10 ×10
9
−
1.3 ×B
10 ×10
9
×0.075
,
4
Notice that the circumferential stress
σ
θθ
does not act on the exposed curved surface of the
disk and hence will not generally be zero at an unloaded edge.
10.2 The thin circular disk 457
from equation (10.23).
Solving these two simultaneous equations for A,B, we obtain
A = 89.87
Ω
2
; B = 0.2653
Ω
2
and hence
σ
rr
=
89.87 −1031r
2
+
0.2653
r
2
Ω
2
σ
θθ
=
89.87 −593.8r
2
−
0.2653
r
2
Ω
2
,
from (10.21, 10.22), where the stresses will be in Pa if r is in metres and
Ω
in radians
per second.
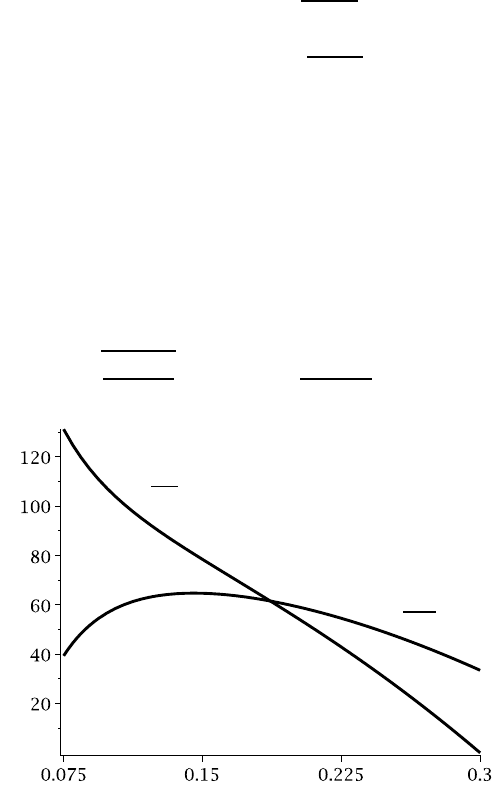
The variation of these two stress components through the disk is illustrated in
Figure 10.4, where we note that the maximum tensile stress is the value of
σ
rr
at the
inner radius r = 0.075 m, given by 131.2
Ω
2
. Setting this equal to the permissible
stress of 10 MPa, we obtain
131.2
Ω
2
max
= 10 ×10
6
and hence the maximum permissible rotational speed is
Ω
max
=
r
10 ×10
6
131.2
= 276 rad/s =
276 ×60
2
π
= 2636 rpm .
σ
rr
Ω
2
Pa s
2
σ
θθ
Ω
2
r (m)
Figure 10.4: Stress distribution in the grinding wheel
458 10 Thick-walled Cylinders and Disks
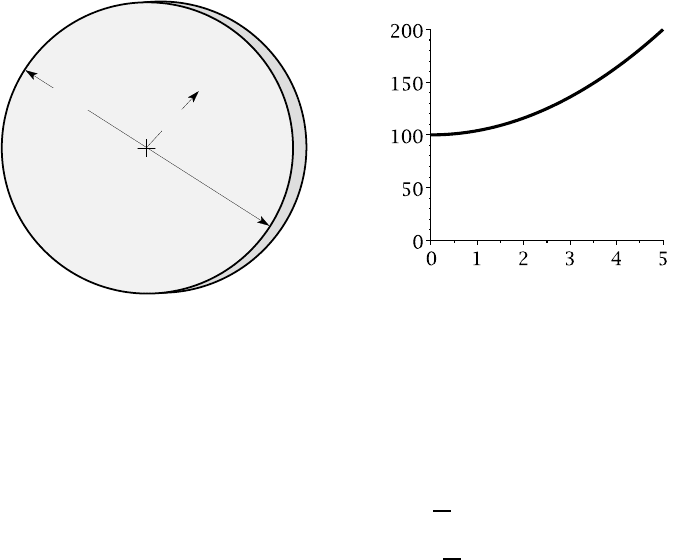
Example 10.2 — Automotive brake disk
An automotive brake disk is idealized as a uniform disk of diameter 10 in., as shown
in Figure 10.5 (a). It is made of cast iron for which E =30×10
6
psi and
α
=7× 10
−6
per
o
F. After a brake application, the temperature distribution, illustrated in Figure
10.5 (b), can be described by the equation T = (100+4r
2
)
o
F, where r is the radial
position in inches. Neglecting stresses due to rotation, find the stress distribution in
the disk and determine the location and magnitude of the maximum shear stress.
10 in.
r
T (
o
F)
r (in.)
(a) (b)
Figure 10.5: The automotive brake disk
General expressions for the stresses are given by equations (10.21, 10.22) as
before. Substituting for T and performing the integrations, we obtain
σ
rr
= −210(50 + r
2
) + A +
B
r
2
σ
θθ
= −210(50 + 3r
2
) + A −
B
r
2
.
The disk has no central hole and hence one boundary condition is lost. However,
an additional condition is obtained from the requirement that the stresses be bounded
at r = 0, which in turn implies that B= 0.
At the outside radius, there is no traction and hence the stress component
σ
rr
=0
as in Example 10.1. It follows that
A = 210(50 + 5
2
) = 15,750 psi .
The complete stress field is therefore
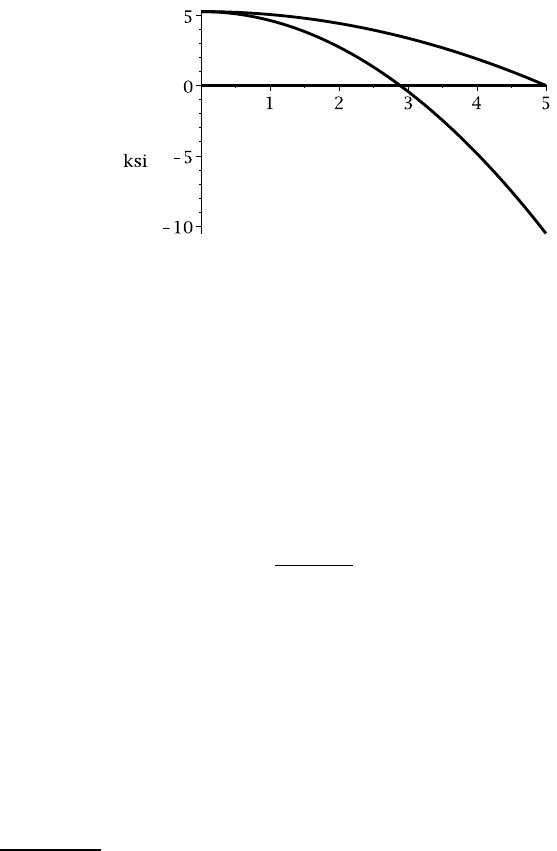
10.2 The thin circular disk 459
σ
rr
= 15750 −210(50 + r
2
) = 5250 −210r
2
σ
θθ
= 15750 −210(50 + 3r
2
) = 5250 −630r
2
,
which is illustrated in Figure 10.6. Notice that the two stress components are equal at
r=0. This is always the case in axisymmetric problems for the disk without a central
hole, since all diameters are equivalent at this point.
5
σ
rr
σ
zz
r (in.)
σ
θθ
Figure 10.6: Stress distribution in the brake disk
We see from Figure 10.6 that the maximum normal stress occurs at r =0 (where
both stress components are 5250 psi tensile) and at the outer radius, where
σ
θθ
is
10,500 psi and compressive (negative). The axisymmetry of the problem ensures that
that there is no shear stress on any of the faces of the element in Figure 10.1 and hence
that
σ
rr
,
σ
θθ
,
σ
zz
are principal stresses. Note that
σ
zz
= 0 for the disk, because of the
plane stress assumption. The maximum shear stress is half of the greatest difference
between principal stresses (see §2.1). All three stresses are shown in Figure 10.6 and
it is clear that the greatest difference between them occurs at the outside radius (r=5
inches) and is
τ
max
=
σ
zz
−
σ
θθ
2
= 5250 psi .
Discussion
These examples are illustrative of the kinds of design calculations that can be per-
formed for circular disks. Notice that we considered only loading due to rotation in
the grinding wheel and only thermoelastic loading in the brake disk, even though
both components experience both rotation and heating during service. To explain
why these choices were made, we first remark that
(i) the terms in the stress equations (10.21, 10.22) due to rotation are proportional
to
ρΩ
2
r
2
;
5
The same argument leads to the conclusion that the membrane stresses
σ
1
,
σ
2
are equal on
the axis for an axisymmetric shell which is continuous across the axis (see Example 8.3).

460 10 Thick-walled Cylinders and Disks
(ii) the thermal stress terms are proportional to E
α
T ;
(iii) a body that is subjected to a uniform increase in temperature increases in size,
but is unstressed unless the boundaries are restrained in some way.
When a car is moving at 60 mph (88 ft/s), the wheels (and hence the brake disks)
will be rotating at about 70 rad/s (670 rpm), where we have assumed a tyre outer ra-
dius of 1.25 ft. This is a low rotational speed and we therefore anticipate a small con-
tribution to the stresses from the rotational terms. To confirm this, calculate
ρΩ
2
r
2
using the largest (outer) radius for r. The density of steel is about 7.4×10
−4
slug/in
3
,
so
ρΩ
2
r
2
= 7.4 ×10
−4
×70
2
×5
2
= 91 psi .
This is small compared with the failure strength of typical steels (≈ 30 ksi) and with
the thermal stresses calculated in Example 10.2.
The grinding wheel is heated at the outer radius as a result of the grinding process.
Grinding wheels are made of ceramic cutting materials bonded by a filler and will
generally have low thermal conductivity. Thus, only the surface layers of the wheel
can be expected to experience a significant increase in temperature. This might cause
significant local circumferential stresses (
σ
θθ
), but they will be compressive since the
material wants to expand and is being prevented from doing so. Brittle materials are
much stronger in compression than in tension. We also see from Example 10.1 above
that the maximum stresses due to rotation occur at the centre of the wheel rather than
the outside, so the questions of possible failure due to rotational stresses and due to
local thermal stresses at the outer edge are independent of each other.
Preliminary thinking of this kind (perhaps supplemented by a few simple esti-
mates) is essential when deciding which stress calculations to perform for design
purposes.
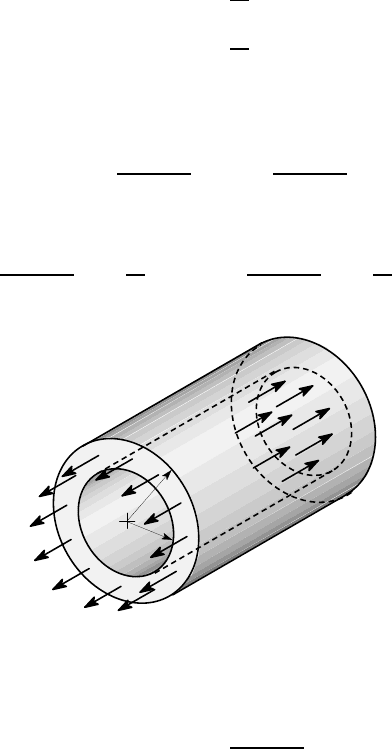
10.3 Cylindrical pressure vessels
Figure 10.7 shows a thick-walled cylindrical vessel of inside radius a and outside
radius b, subjected to internal pressure p
0
. Vessels of this kind are only needed when
the pressure to be contained is very large. Boilers, gas tanks etc. generally oper-
ate at pressures small enough to permit the wall thickness to be small in compari-
son with the radius, in which case the simpler membrane theory of Chapter 8 can
be used. Applications of thick-walled vessels include processes requiring extremely
high pressure, such as the manufacture of synthetic diamonds, and testing machines
to determine the properties of materials under high hydostatic pressure.
6
6
An important case is the determination of the viscosity of lubricants. In gearing and rolling
contact bearings, the lubricant is squeezed to very high pressure and successful lubrication
for such applications depends on the lubricant having a high viscosity at high pressures.

10.3 Cylindrical pressure vessels 461
r
a
b
p
0
Figure 10.7: Cylindrical vessel with internal pressure p
0
If the ends of the vessel are prevented from moving, the plane strain constitutive
relations (10.12, 10.13) are appropriate. These differ from the corresponding plane
stress relations (10.14, 10.15) only in the multiplying constants and hence, mathe-
matically, a problem in plane strain simply looks like a plane stress problem for a
material with different material properties. In fact, it is easily verified that equations
(10.12, 10.13) can be obtained from (10.14, 10.15) by making the substitutions
E =
E
′
(1 −
ν
′2
)
;
ν
=
ν
′
(1 −
ν
′
)
;
α
=
α
′
(1 +
ν
′
) (10.24)
and then dropping the primes.
It follows that the stresses and displacements in the cylinder can be obtained by
making the same substitutions in equations (10.21–10.23) and are
σ
rr
= −
(3 −2
ν
)
ρΩ
2
r
2
8(1 −
ν
)
−
E
α
(1 −
ν
)r
2
Z
rT dr + A +
B
r
2
(10.25)
σ
θθ
=−
(1+2
ν
)
ρΩ
2
r
2
8(1−
ν
)
+
E
α
(1 −
ν
)r
2
Z
rT dr−
E
α
T
(1−
ν
)
+A−
B
r
2
(10.26)
u
r
= −
(1 −2
ν
)(1 +
ν
)
ρΩ
2
r
3
8E(1 −
ν
)
+
α
(1 +
ν
)
(1 −
ν
)r
Z
rT dr
+
A(1 −2
ν
)(1 +
ν
)r
E
−
(1 +
ν
)B
Er
. (10.27)
For the problem of the thick-walled cylinder, we might also be interested in the
axial stress
σ
zz
, which can be obtained from (10.11) as
σ
zz
=
ν
(
σ
rr
+
σ
θθ
) −E
α
T
= −
νρΩ
2
r
2
2(1 −
ν
)
−
E
α
T
(1 −
ν
)
+ 2
ν
A . (10.28)
462 10 Thick-walled Cylinders and Disks
If there are no thermal or rotational effects, only the terms involving the constants
A,B will remain and these are determined by imposing boundary conditions at the
inner and outer surfaces, i.e.
σ
rr
(a) = A +
B
a
2
= −p
0
σ
rr
(b) = A +
B
b
2
= 0 .
Notice that the pressure on the inner surface corresponds to a compressive stress and
is therefore negative. Solving these equations for A,B, we obtain
A =
a
2
p
0
(b
2
−a
2
)
; B = −
a
2
b
2
p
0
(b
2
−a
2
)
(10.29)
and hence
σ
rr
=
a
2
p
0
(b
2
−a
2
)
1 −
b
2
r
2
;
σ
θθ
=
a
2
p
0
(b
2
−a
2
)
1 +
b
2
r
2
. (10.30)
a
b
zz
σ
p
0
Figure 10.8: Free-body diagram for determining
σ
zz
If the ends of the cylinder are prevented from moving, the axial stress is given by
equation (10.28) as
σ
zz
= 2
ν
A =
2
ν
p
0
a
2
(b
2
−a
2
)
and it is constant, i.e. it doesn’t vary with radius r. However, we can generalize the
solution to other end conditions by superposing a state of uniaxial tension, which
will change
σ
zz
by a constant without affecting the other two stress components
(though it will change the radial displacement u
r
, because of Poisson’s ratio strains).
The resulting axial stress will still be independent of r and hence it can be found
by considering the axial equilibrium of the cylinder. For example, if the vessel has
closed ends and there are no external loads applied, the axial equilibrium of the free-
body diagram of Figure 10.8 yields the equation
10.3 Cylindrical pressure vessels 463
π
(b
2
−a
2
)
σ
zz
−
π
a
2
p
0
= 0 ,
which states that the force exerted by the pressure p
0
on the end face (of area
π
a
2
)
is balanced by the force exerted by the axial stress over the annular cross section of
the vessel [area
π
(b
2
−a
2
)]. It follows that
σ
zz
=
a
2
p
0
(b
2
−a
2
)
. (10.31)
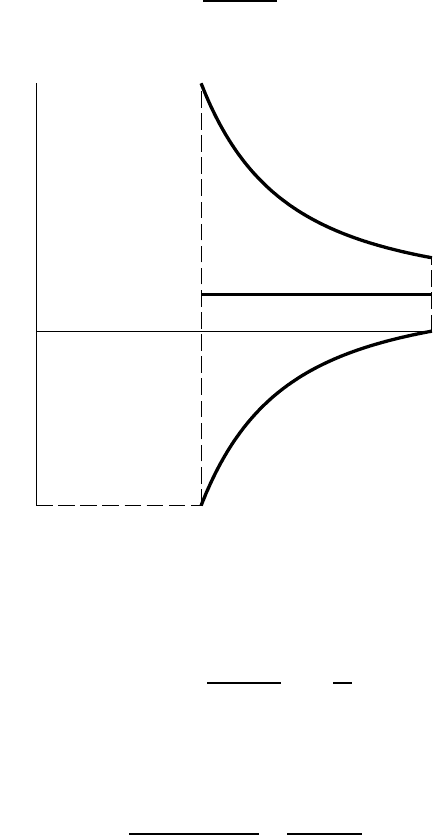
σ
θθ
σ
zz
0
a r b
σ
rr
−p
0
Figure 10.9: Stress distribution in the cylindrical vessel
The three stress components
σ
rr
,
σ
θθ
,
σ
zz
are presented graphically in Figure
10.9. Notice that the maximum tensile stress is
σ
θθ
at the inner radius, r = a, and
is
σ
max
=
σ
θθ
(a) =
a
2
p
0
(b
2
−a
2
)
1 +
b
2
a
2
,
from equation (10.30).
Also, the maximum difference between principal stresses is (
σ
θθ
−
σ
rr
) at the
same location leading to
τ
max
=
σ
θθ
(a) −
σ
rr
(a)
2
=
2b
2
p
0
(b
2
−a
2
)
.
Thus, ductile failure is most likely to initiate at the inner radius r = a.

464 10 Thick-walled Cylinders and Disks
10.4 Composite cylinders, limits and fits
There are situations where it is advantageous to use an assembly of two concentric
cylinders or disks, as shown in Figure 10.10. Usually, the central hole (inside di-
ameter) of the outer cylinder is made slightly smaller than the outside diameter of
the inner cylinder, so as to ensure that there is a firm fit between the components.
Assembly can be achieved by forcing the cylinders together axially (usually using a
lubricant) or by heating the outer cylinder
7
and/or cooling the inner one sufficiently
for them to be assembled without force.
Figure 10.10: A composite cylinder
Advantages of using a composite cylinder assembly include
(i) It is a convenient way of mounting gears, pulleys and wheels on shafts. If the
contact pressure at the interface after assembly is sufficiently large, it may not
even be necessary to use a key to transmit torque, since high friction forces can
be transmitted.
(ii) The two cylinders could be of different materials. For example, a corrosion-
resistant (but possibly brittle) material could be used for the inner cylinder (to be
in contact with a contained corrosive fluid) and a structurally strong material for
the outer cylinder.
(iii) The pre-stress developed by the assembly process is beneficial and permits a
composite cylinder with given inner and outer diameters to carry a larger internal
pressure than a monolithic cylinder of the same material.
10.4.1 Solution procedure
Each of the two components of the cylinder or disk can be analyzed using the meth-
ods developed above. The stress and displacement fields will still be given by equa-
tions (10.21–10.23) or (10.25–10.27), but the arbitrary constants A, B will generally
7
Notice that when the outer cylinder is heated to a uniform temperature, all the dimensions,
including the diameter of the hole, get bigger.
