Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

Problems 445

cylinder

transition

sphere

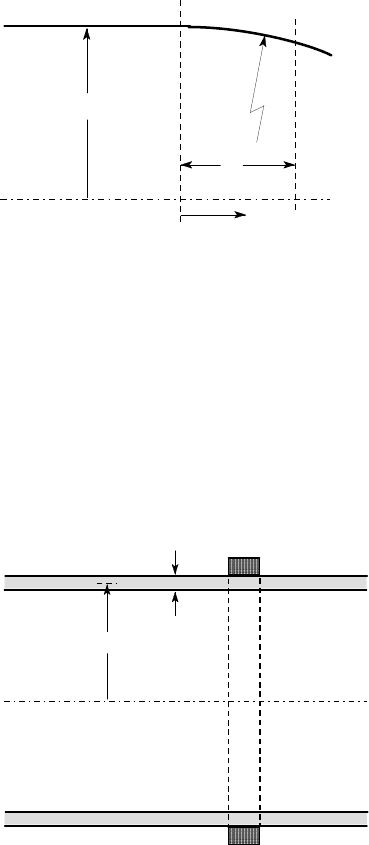
Figure P9.10

Find the bending moment at z=0, using the argument of §9.6.1 [equation (9.33)],

assuming that

b ≫1.

Discuss the relative beneﬁts to be gained from such a transition.

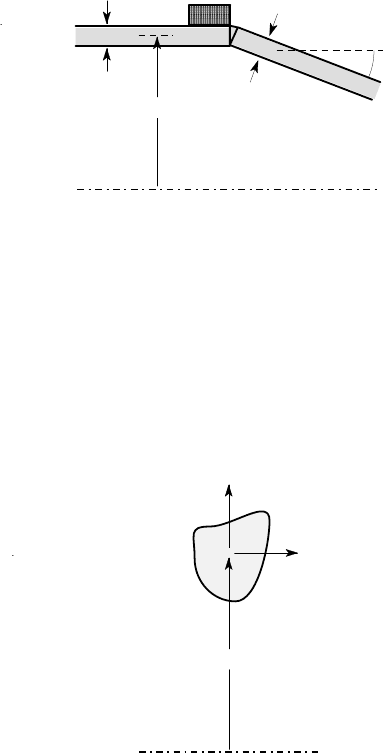
9.11. A long shell of radius 500 mm and thickness 2 mm is locally stiffened by a

reinforcing ring of 15 mm×10 mm rectangular cross section, as shown in Figure

P9.11. The shell is subjected to an internal pressure p

= 400 kPa. Both the ring and

the shell are made of steel for which E =210 GPa,

=0.3.

15 mm

10 mm

2 mm

500 mm

p = 400 kPa

Figure P9.11

(i) Find the membrane displacement u

in the unstiffened shell;

(ii) Assuming the ring can be treated as rigid, ﬁnd the radial force F

per unit cir-

cumference exerted on the ring by the shell;

(iii) Use equation (9.35) to determine the radial displacement of the ring due to this

force. Does your result support the ‘rigid’ assumption used in (ii)?

446 9 Axisymmetric Bending of Cylindrical Shells

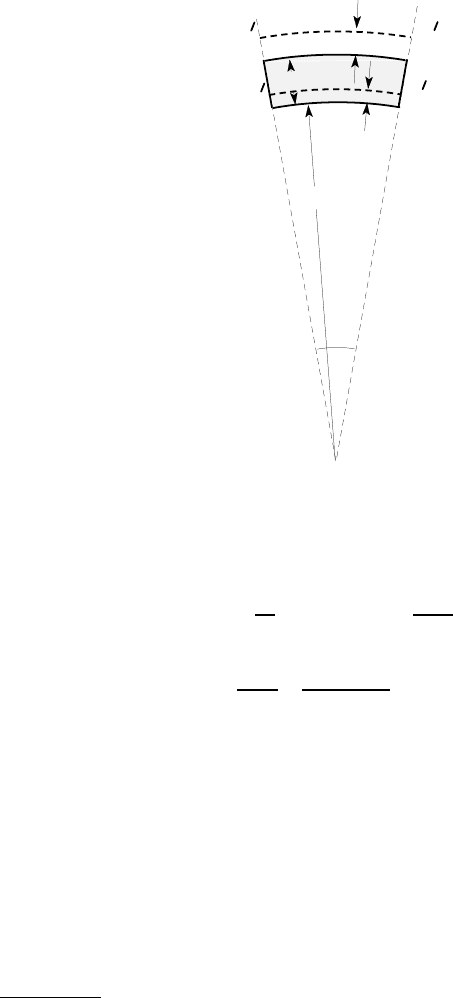
9.12. Figure P9.12 shows a transition from a cylindrical shell of radius a to a coni-

cal shell of semi-angle

, stiffened by a reinforcing ring. Both shell segments have

thickness t and are made of the same material as the ring.

(i) Find the unbalanced radial force F

per unit circumference that must be resisted

by the ring if the shell is loaded by an internal pressure p

;

(ii) Estimate the required cross-sectional area of the ring if the radial displacement

at the transition is to be limited to 10% of the membrane displacement u

in the

cylindrical segment.

internal pressure p

Figure P9.12

9.13. Figure P9.13 shows the cross section of a reinforcing ring whose mean radius

(i.e. the radius to the centroid of the section, C) is a.

Determine the circumferential strain e

θθ

as a function of the coordinates

the mean radius increases by u

whilst the section remains undistorted. Hence deter-

mine the radial force per unit circumference required to achieve this deformation, if

the material has Young’s modulus E. Assume that the dimensions of the cross section

are small compared with a.

Figure P9.13

Problems 447

9.14. The ring cross section of Figure P9.1 3 is now rotated in the plane of the ﬁgure

about the centroid C through a n angle

. As before, determine th e circum ferential

strain e

θθ

as a function of the coordinates

. Hence determine the moment M

per

unit circumferen ce that must be applied to the ring to achieve this rotation. Compare

your result with equation (9.35) in the special case of a rectangu la r section b ×c.

Section 9.7

9.15. A heat exchanger tube of radius 60 mm and thickness 3 mm is made of copp er

(E = 121 GPa,

= 0.33,

= 17×10

−6

per

C, K = 381 W/m

C). Th e temperatures

of the outside and inside surfaces of the tube T

out

vary with axial distance z from

the end ac cording to the e quations

out

= 150

C ; T

= 30 + 120 e

−

z o

C ,

where

=0.8 m

−1

and z is measured in metres.

The end of the tube is free of load and there is no internal or external pressure.

Find the maximum tensile stress in the tube.

9.16. A long cylindrical shell of radius 200 mm and thickness 6 mm has a rigid (built-

in) e nd at z = 0. T he temperature of the shell varies lin early with z according to the

equation

T (z) = 100z

C ,

where z is measured in metres. There is no internal pressure.

Find the maximum tensile stress in the shell if the relevant material prope rties

are E = 72 GPa,

=0.32,

=22×10

−6

per

9.17. The c entral section −b < z <b of a long cylindrical shell of radius a and thick-

ness t is heated to a mean temperature T

, the rest o f the shell being at zero temper-

ature. Find the radial displacement of the shell and the axial be nding moment M

the p oint z =0.

Thick-walled Cylinders and Disks

In this chapter, we shall consider a class of problems in which the stresses and dis-

placements depend only on the radius r in the cylindrical coordinate system (r,

,z).

The problems are therefore axisymmetric (i.e. there is no variation with the angle

)

nor is there any variation with the distance z along the axis.

Practical applications include a thick-walled cylinder loaded by internal or ex-

ternal pressure, a cylindrical grinding wheel loaded as a result of centrifugal accel-

eration during rotation, an automotive brake disk with an axisymmetric temperature

distribution due to frictional heating, or the contact stresses developed when a cylin-

drical wheel is shrunk or pressed onto a cylindrical shaft.

10.1 Solution method

These applications are of considerable importance in their own right, but the study

of axisymmetric problems has the additional advantage of introducing the reader to

the methods used in the more advanced theories of elasticity, thermoelasticity and

plasticity in a conveniently simple context.

The solution depends on the following three physical requirements:

(i) Each particle of the body must satisfy Newton’s second law. This imposes a con-

dition on the stress ﬁeld in the body, since the tractions on the imaginary surface

deﬁning a particle are actually stress components. If there are no accelerations,

this is an equilibrium condition.

(ii) The stresses and strains are related by a constitutive law for the material, which

can be determined by performing appropriate experiments on idealized speci-

mens. In the linear elastic r´egime, this will be Hooke’s law [equations (1.14–

1.16)], but we shall also consider problems in the plastic r´egime for elastic-

perfectly plastic materials (§5.2.3), for which the constitutive law is the yield

criterion for the material (§2.2.3).

(iii) The deformation must be kinematically possible, which places constraints on

the admissible strain distributions. This is sometimes known as the compatibility

condition.

J.R. Barber, Intermediate Mechanics of Materials, Solid Mechanics and Its Applications 175,

2nd ed., DOI 10.1007/978-94-007-0295-0_10, © Springer Science+Business Media B.V. 2011

450 10 Thick-walled Cylinders and Disks

10.1.1 Stress components and the equilibrium condition

Figure 10.1 shows a small element of material in the cylindrical polar coordinate

system (r,

,z). For axisymmetric loading, there can be no shear stresses acting on

the faces of this element and the only non-zero stress components are the normal

stresses

θθ

, which are independent of

and z, but which generally vary

with radius r. This is recognized in the ﬁgure by the inclusion of the difference

δσ

between the normal stresses on the inner and outer curved surfaces of the element.

δθ

δr

δz

σ + δσ

θθ

Figure 10.1: Stress components in polar coordinates

The stress component

δσ

acts over a ‘rectangular’ curved surface of

area (r +

δθδ

z and therefore exerts a radially-outwards force (

δσ

)(r +

δθδ

z, if

δθ

is sufﬁciently small. The forces acting on the other faces of the ele-

ment can be found in the same way. Summing the forces in the radial direction, we

can write Newton’s law in the form

(

δσ

)(r +

δθδ

z −

δθδ

z −2

θθ

zsin



δθ



δθδ

z ,

(10.1)

where

is the density of the material and a

is the outward radial acceleration of the

element. In interpreting this equation, notice that

10.1 Solution method 451

(i) The forces

θθ

z associated with the stress component

θθ

are not co-linear

because of the curvature of the element and they therefore have a resultant in the

inward radial direction.

(ii) The volume of the element is r

δθδ

z and hence its mass is

δθδ

The only state of motion leading to an axisymmetric stress ﬁeld is that of uniform

rotation about the axis at speed

Ω

, in which case

= −

Ω

r . (10.2)

We now substitute (10.2) into (10.1), divide both sides of the equation by

δθδ

z, and take the limit as the small quantities

δθ

→0, obtaining the dif-

ferential equation of motion

(

−

θθ

)

= −

ρΩ

r . (10.3)

In the special case where the body is not rotating (

Ω

= 0), this reduces to the

equilibrium equation

(

−

θθ

)

= 0 . (10.4)

10.1.2 Strain, displacement and compatibility

For axisymmetric loading, the most general deformation that can occur in the plane

involves only a radial displacement u

that is a function of r only. The normal strains

θθ

can be written in terms of u

by considering the kinematics of the small ele-

ment ABCD in Figure 10.2, which deforms to the conﬁguration A

′

as a result

of the radial displacement u

. Notice that the arc

δθ

cannot change, since a sequence

of elements around the circumference must add up to 2

and in axisymmetry the

deformation of all elements is identical.

Writing the two strains as (extension)/(original length) for this element and then

proceeding to the limit as

δθ

→0 we obtain

= lim

r→0

(r +

r) −u

(r)

(10.5)

θθ

= lim

δ θ

→0

(r + u

)

δθ

−r

δθ

. (10.6)

A similar argument was used in the derivation of the equilibrium equation (8.2) for mem-

brane stresses in §8.2.

452 10 Thick-walled Cylinders and Disks

δθ

δr

u (r)

u (r + δr)

Figure 10.2: Deformation associated with a radial displacement

The two strains e

θθ

are deﬁned in terms of one displacement component u

and we can therefore eliminate u

between equations (10.5, 10.6), obtaining

(re

θθ

) = e

θθ

+ r

θθ

−e

)

= 0 . (10.7)

This is the compatibility equation for strains. It deﬁnes the condition that the

strain components must satisfy if the particles of the body are to ﬁt together in the

deformed state.

10.1.3 The elastic constitutive law

The equilibrium equation (10.4) [or the equation of motion (10.3)] relates the two

stress components

θθ

, whereas the compatibility equation (10.7) relates the

two strain components e

θθ

. We need two equations to solve for two unknowns

and we can therefore solve this problem in terms of either stress or strain if the

relation between stress and strain (also known as the constitutive law) is known for

For a discussion of compatibility equations in more general problems of elasticity, see J.R.

Barber (2010), Elasticity, Springer, Dordrecht, Netherlands, 3rd edn., §2.2.

10.1 Solution method 453

the material. Alternatively, we can use the strain-displacement relations (10.5, 10.6)

and the constitutive law to express the stresses as functions of the single displacement

component u

, which is then determined from equation (10.3) or (10.4).

Notice that equations (10.3–10.7) are essentially mathematical relations, whereas

the constitutive law is a property of the real material that must be found by an exper-

iment such as a tensile test.

If the stresses are sufﬁciently small, most materials behave elastically and obey

Hooke’s law [equations (1.14–1.16)], which in polar coordinates can be written in

the form

−

νσ

θθ

−

νσ

T (10.8)

θθ

−

νσ

−

νσ

T (10.9)

−

νσ

−

νσ

θθ

T , (10.10)

where T should here be interpreted as the change in temperature from a datum at

which the nominal geometry is deﬁned.

Notice that each stress component produces

a strain in its own direction, but also a ‘Poisson’s ratio’ strain of opposite sign in the

two orthogonal directions.

Plane stress and plane strain

The only state in which the stresses are truly independent of z is that in which expan-

sion in the z-direction is prevented, so that e

= 0. This is known as a state of plane

strain. Equation (10.10) can then be solved for

, with the result

(

θθ

) −E

T . (10.11)

Substituting this result into (10.8, 10.9), we obtain

(1 −

)

−

(1 +

)

θθ

(1 +

)T (10.12)

θθ

(1 −

)

θθ

−

(1 +

)

(1 +

)T . (10.13)

These are the two-dimensional constitutive relations for axisymmetric plane strain.

Alternatively, if the cylinder is very short in the axial direction and the z-surfaces

are free of traction, it can be argued that

will always be small and hence can be

neglected. This leads to an approximate solution appropriate for a thin disk and is

known as a state of plane stress. Setting

=0, we obtain

−

νσ

θθ

T (10.14)

θθ

−

νσ

T , (10.15)

In §1.5.4, we made this explicit by using the notation

∆

T .

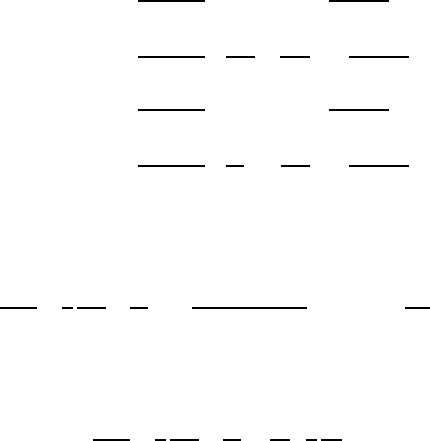
454 10 Thick-walled Cylinders and Disks

which are the two-dimensional constitutive relations for axisymmetric plane stress.

The perceptive reader should immediately ask the question “How thin must the

disk be for the plane stress approximation to be appropriate?” Clearly the answer

cannot depend on the particular choice of units used to measure the thickness and

hence must be stated in terms of an appropriate dimensionless ratio between the

thickness and another signiﬁcant dimension of the disk. In particular, the thickness

needs to be small in comparison with the the inner and outer radii of the disk.

Comparing the relations (10.12, 10.13) and (10.14, 10.15), we notice that they

are both linear equations connecting the same variables. They differ only in the mul-

tiplying constants. Thus, the mathematical solution procedure is the same for both

plane stress and plane strain problems.

10.2 The thin circular disk

In this section, we shall develop elastic solutions for the thin circular disk using the

plane stress approximation — i.e. using the constitutive law of equations (10.14,

10.15). The results will be applicable to thin rotating or stationary disks with arbi-

trary axisymmetric temperature distributions. Typical applications include automo-

tive brake disks, grinding wheels and turbine blade disks.

We ﬁrst solve equations (10.14, 10.15) for

θθ

and use (10.5, 10.6) to express

the results in terms of u

, obtaining

(1 −

)

θθ

) −

(1 −

)

(1 −

)





−

(1 −

)

(10.16)

θθ

(1 −

)

θθ

) −

(1 −

)

(1 −

)





−

(1 −

)

. (10.17)

Substituting these expressions into the equation of motion (10.3), we obtain the

ordinary differential equation

−

= −

ρΩ

(1 −

(1 +

)

, (10.18)

for the radial displacement, u

The general solution of this equation can be obtained using the identity

−



(ru

)



which can be veriﬁed by expanding the right hand side, using differentiation by parts.