Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

Problems 415

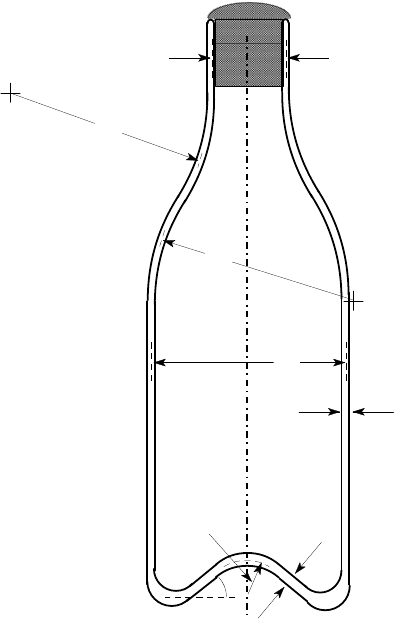
8.16. Figure P8.16 shows the approximate dimensions of a champagne bottle, man-

ufactured from glass of density

= 2400 kg/m

. The bottle is to contain liquid of

density 1050 kg/m

at a pressure of 30 kPa above atmospheric.

Which of the following quantities are signiﬁcant enough to require inclusion in a

membrane stress calculation:-

(i) internal pressure,

(ii) weight of contents,

(iii) weight of the glass.

Estimate the maximum membrane stress in the bottle. Why is it necessary to use

an increased wall thickness at the points A−A?

all dimensions in mm

Figure P8.16

15 radius

416 8 Membrane Stresses in Axisymmetric Shells

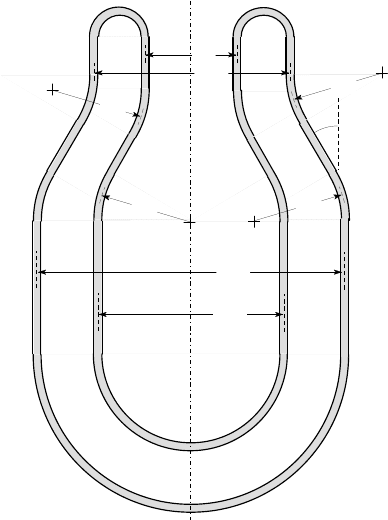
8.17. Figure P8.17 shows the cross section of a vacuum ﬂask for the temporary stor-

age of liquiﬁed gasses. The space A between the inner and outer walls is evacuated

and the exposed surfaces are subject to atmospheric pressure of 100 kPa. The vessel

is made of glass of density 2300 kg/m

and the wall thickness is everywhere 3 mm,

except at B where the vessel must be stiffened against bending.

Find the maximum tensile membrane stress in the wall, excluding the region B.

170

260

160

all dimensions in mm

Figure P8.17

Section 8.5

8.18. Figure P8.18 shows a thin-walled conical shell of thickness t, semi-angle

and

height h. It is loaded by self-weight only, the material of the shell having density

Young’s modulus E and Poisson’s ratio

Determine the membrane stresses

at the base of the shell and hence ﬁnd

the radial displacement u

at the base of the shell.

Note: The surface area of a cone of semi-angle

and height h is

tan

/cos

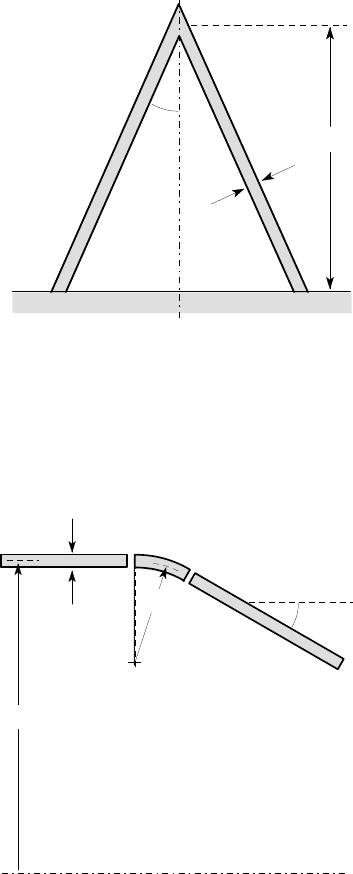
Problems 417

Figure P8.18

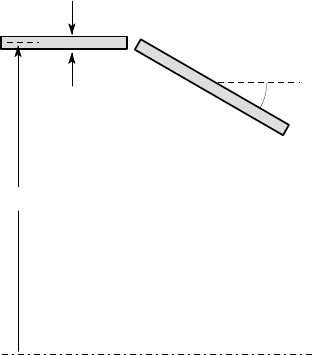
8.19. For the toroidal transition between the cylinder and the cone shown in Fig-

ure P8.19, ﬁnd the membrane stresses

at the points A

, due to an

internal pressure of 1 MPa, if the wall thickness is 10 mm.

300

1000

all dimensions in mm

Figure P8.19

Hence ﬁnd the circumferential strain and the radial displacement at these points,

if the material is steel (E =210 GPa,

=0.3).

Sketch the distorted shapes of the shell sections at the transition and show how

local bending will re-establish continuity of displacement.

418 8 Membrane Stresses in Axisymmetric Shells

8.20. Repeat the calculation of Problem 8.19 for the points A

, assuming there is

no toroidal transition — i.e. the cone is directly joined to the cylinder as shown in

Figure P8.20.

1000

all dimensions in mm

Figure P8.20

Comment on the relation between the answers to Problems 8.19, 8.20. Will the tran-

sition reduce the local bending stresses, as we would intuitively expect, or not? If so,

explain what is missing in the argument of Problem 8.20.

8.21. A cylindrical shell of radius a, thickness t is to be capped by a hemispherical

shell of radius a and thickness t

. It is proposed to eliminate the bending effects at

the discontinuity, discussed in §8.5.1, by choosing t

so as to cause the membrane

radial displacements u

in the cylinder and the hemisphere to be equal. What is the

required ratio t

/t, if the material has Young’s modulus E and Poisson’s ratio

8.22. A spherical shell of mean radius a and thickness t rotates at angular velocity

Ω

about a diameter. There is no internal pressure.

Find the membrane stresses as functions of polar angle and hence ﬁnd the radial

displacement at the equator. The material has density

, Young’s modulus E and

Poisson’s ratio

Axisymmetric Bending of Cylindrical Shells

We saw in the last chapter that the equilibrium equations for an axisymmetric shell

can be satisﬁed by membrane stresses

, which are uniform through the thick-

ness of the shell. However, the radial displacements predicted by the membrane

theory generally involve discontinuities at the supports or wherever there is a dis-

continuity in radius or thickness. In such cases, continuity is restored by localized

bending of the shell. In the present chapter, we shall investigate the axisymmetric

bending of cylindrical shells, but important features of the results carry over to other

axisymmetric shell bending problems.

9.1 Bending stresses and moments

As in the bending of beams, shell bending involves stresses that vary linearly through

the shell thickness. In combination with the membrane stresses, they constitute the

ﬁrst two terms in a Taylor series expansion of the variation of normal stress through

the thickness.

θθ

Figure 9.1: Coordinate system and stresses for a shell element

J.R. Barber, Intermediate Mechanics of Materials, Solid Mechanics and Its Applications 175,

2nd ed., DOI 10.1007/978-94-007-0295-0_9, © Springer Science+Business Media B.V. 2011

420 9 Axisymmetric Bending of Cylindrical Shells

Figure 9.1 shows the longitudinal stress

and the circumferential stress

θθ

acting on an element of cylindrical shell of mean radius a. To decouple membrane

and bending stresses, it is convenient to deﬁne a coordinate

in the direction of the

outward normal and measured from the mid-plane of the shell. In other words, the

distance from the cylinder axis is r = a+

. This is equivalent to the location of the

origin at the centroid in beam bending problems. The bending theory is then based

on the assumption that the local stress ﬁeld can be written in the form

(9.1)

θθ

, (9.2)

where the constant terms

are the membrane stresses already deﬁned in Chapter

8, and the linearly varying terms represent the bending stresses.

The stress

θθ

in equation (9.2) has a resultant bending moment M

per unit

length of shell, given by

t/2

−t/2

θθ

t/2

−t/2





. (9.3)

We can use this result to eliminate s

in equation (9.2), obtaining

θθ

12M

. (9.4)

A similar procedure with

gives

12M

, (9.5)

where M

is the bending moment per unit circumference. Notice that M

are

bending moments per unit length and hence they have units of force (e.g. Nm per m

≡ N). They act on the edges of the shell element in the sense deﬁned in Figure 9.2.

Figure 9.2: Bending moments acting on the shell element

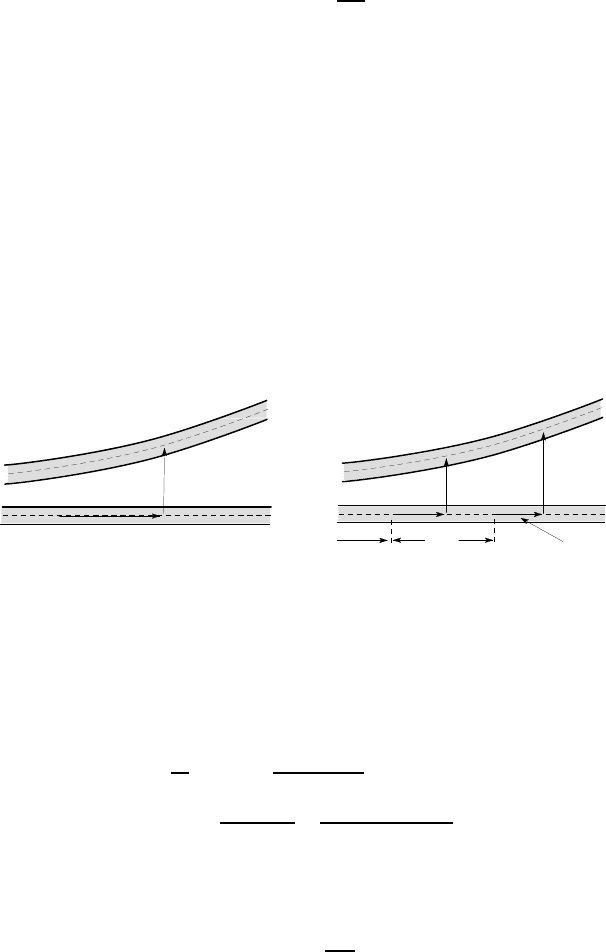
9.2 Deformation of the shell 421

The sign convention is chosen such that positive moments generate tensile

stresses at the outside of the shell, where

> 0. The maximum bending stresses

occur at

=±t/2 and are

max

= ±

. (9.6)

The bending stresses are additive to the membrane stresses [see equations (9.1, 9.2)],

so generally we shall ﬁnd that the maximum total stress in a shell will occur in a

region of localized bending.

9.2 Deformation of the shell

A general axisymmetric deformation of a cylindrical shell can be characterized by

the radial and axial displacements, u

and u

respectively, of the shell mean surface

as functions of the axial co-ordinate z. These displacements are illustrated in Figure

9.3 (a), where the horizontal straight line represents the position of the shell mean

surface before deformation. The point A on this line moves to A

′

as a result of com-

bined membrane and bending deformations.

δz

(z)

(z+δz)

(z)

(z+δz)

(a) (b)

Figure 9.3: (a) Deﬁnition of displacement components, (b) deformation of the shell

element AB

The cross section of the cylinder remains circular and, as in §8.5, we conclude

that the circumferential strain e

θθ

/a. Hooke’s law then gives

= e

θθ

−

νσ

−

νσ

12(M

−

)

. (9.7)

We argued in Example 8.2 that the radial stress

is negligible compared with

θθ

and hence the corresponding radial strain,

∂

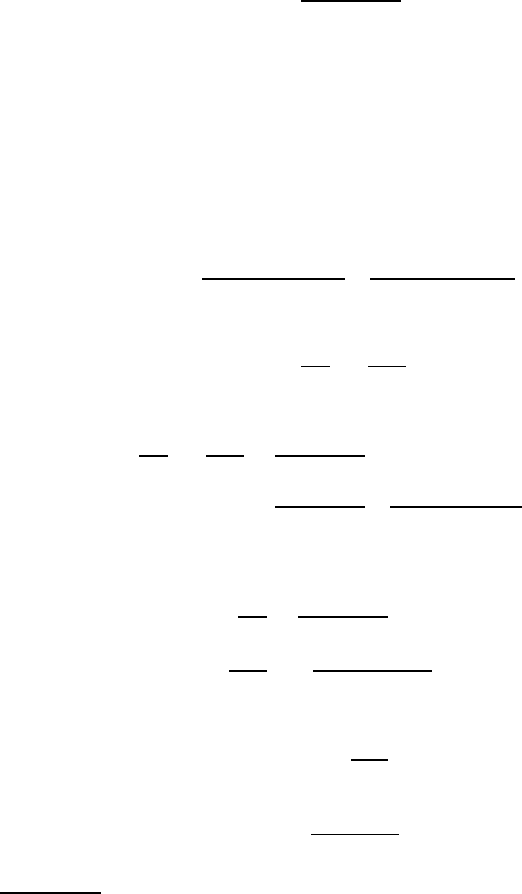
422 9 Axisymmetric Bending of Cylindrical Shells

is also negligible.

It follows that u

cannot be a function of

, so the term varying

with

in equation (9.7) must be zero, leading to the results

(9.8)

(

−

νσ

. (9.9)

As in the elementary bending theory, we assume that plane transverse sections

remain plane and perpendicular to the local shell wall. The deformation of a typical

element AB of length

z is shown in Figure 9.3 (b). The mean line increases in length

by the amount

(z +

z) −u

(z)

and the section at B rotates anticlockwise relative to that at A through the angle

′

(z +

z) −u

′

where u

′

≡du

/dz. The longitudinal strain is therefore

(z +

z) −u

(z)

−

′

(z +

z) −u

′

]

and in the limit

z →0 we have

−

Using this result and Hooke’s law, we obtain

−

νσ

θθ

(

−

νσ

)

12(M

−

)

, (9.10)

from equations (9.4, 9.5). This equation must be satisﬁed for all z,

, so we can

equate coefﬁcients of

, obtaining

(

−

νσ

)

(9.11)

= −

12(M

−

)

. (9.12)

Furthermore, we can eliminate M

from (9.12) using (9.8), with the result

= −D

, (9.13)

where

D =

12(1 −

)

(9.14)

is known as the stiffness of the shell.

It might be argued that the membrane stresses

will generate a non-negligible Pois-

son’s ratio strain e

. However, a more rigorous treatment including this effect shows that

the resulting modiﬁcation of equation (9.8) is still small of order t/a (see Problem 9.1).

9.3 Equilibrium of the shell element 423

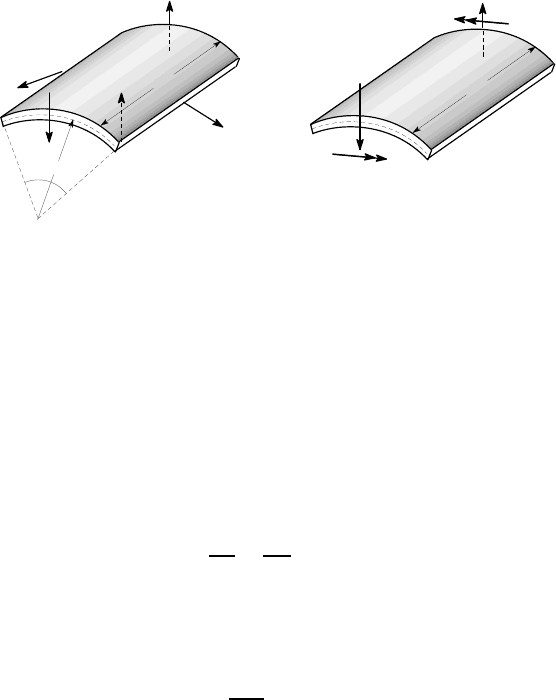
9.3 Equilibrium of the shell element

As in §8.2, we can write an equilibrium equation for the forces acting on the shell

element in the normal direction, but when bending is included this equation will also

include transverse shear forces. Figure 9.4 (a) shows the appropriate forces acting on

the element a

δθδ

z. Notice that the lengths

y in Figure 8.8 are here replaced by

z,a

δθ

respectively. We also include transverse shear forces V (z) per unit length on

the curved edges of the element. There can be no shear forces on the straight edges

because the deformation is axisymmetric.

δθ

V(z)aδθ

V(z+δz)aδθ

paδθδz

δz

σ tδz

δz

Vaδθ

M(z)aδθ

M(z+δz)aδθ

(a) (b)

Figure 9.4: Equilibrium of (a) forces and (b) moments on the shell element

Summing the forces in the direction of the outward normal, we obtain

[V (z +

z) −V(z)]a

δθ

+ pa

δθδ

z −

δθ

= 0 .

Here, the second term arises from the internal pressure p acting on the area a

δθδ

and the last term is the resultant of the two forces

z and is obtained exactly as in

the derivation of equation (8.2).

Dividing through by a

δθδ

z and taking the limit as

z→0, we obtain

− p . (9.15)

A second equation is obtained by considering the moment equilibrium of the

element under the action of the bending moments and shear forces shown in Figure

9.4 (b). We obtain

= V . (9.16)

Alternatively, this result can be considered as another case of equation (6.1), regard-

ing the shell element as a beam of unit width.

424 9 Axisymmetric Bending of Cylindrical Shells

9.4 The governing equation

These equations can be expressed in terms of the radial displacement u

, to obtain

the governing equation for shell deformation. We ﬁrst note that

νσ

, (9.17)

from equation (9.9) and hence

νσ

− p , (9.18)

from (9.15). We can also use equation (9.13) to write (9.16) in terms of u

, obtaining

V =

= −D

. (9.19)

Eliminating V between (9.18, 9.19), we then obtain

−D

νσ

− p .

This is conveniently rearranged in the form

+ 4

= 4



−

νσ



, (9.20)

where we deﬁne

3(1 −

)

(9.21)

and we have used (9.14) to simplify the multiplying constants. Equation (9.20) is the

governing equation for axisymmetric bending of a circular cylindrical shell of radius

a and thickness t.

Figure 9.5: The shell considered as a set of connected beams