Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

8.2 The circumferential stress 395

sectional cut (e.g. A−A in Figure 8.4) and it corresponds to a line perpendicular to

the axis of symmetry. By contrast, the radius R

is perpendicular to the local tangent

to the shell.

A particular case that demonstrates this distinction is the sphere. Everyone would

agree from symmetry that a sphere of radius a has its principal radii equal at all points

— i.e. that R

= R

= a. However, if we think of the sphere as a special case of an

axisymmetric shell, we would immediately determine R

=a, but the radius r would

then vary depending on whether we were looking near the poles or near the equator

[see Figure 8.12 (b)].

shell wall

= a

(a) (b)

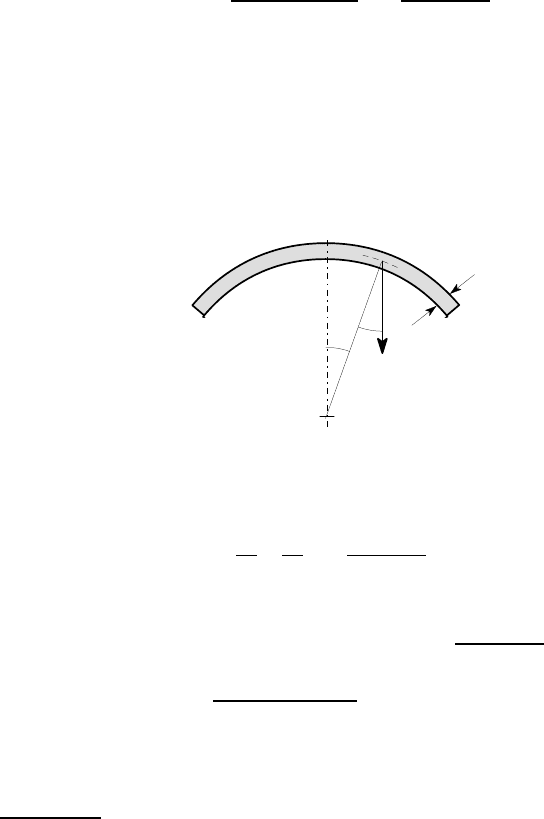
Figure 8.12: (a) Distinction between the cross-sectional radius r and the circumfer-

ential radius of curvature of the shell R

, (b) Radii r and R

for the sphere

By contrast, if we construct the normal to the shell at any point and deﬁne R

as the distance along the normal to the axis of symmetry, we see that this leads to

the correct conclusion that R

= a and that the centres O

for both radii lie at the

centre of the sphere for all points on the surface.

8.2.2 Sign conventions

The formula

(8.2)

was obtained under the assumptions that

are tensile positive and that the cen-

tres O

corresponding to the radii R

are both on the same side of the shell as

the pressure p.

Sometimes the two centres are on opposite sides of the shell, in which case the

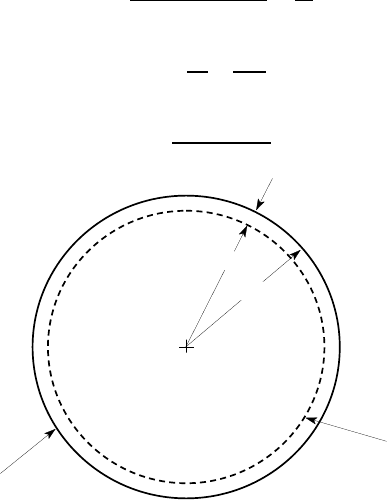
surface is locally saddle-shaped, as shown in Figure 8.13. Consider, for example

the inside surface of a doughnut. This kind of curvature is sometimes referred to as

anticlastic.

396 8 Membrane Stresses in Axisymmetric Shells

Figure 8.13: Shell element with anticlastic curvature

In addition, the pressure — if there is one – may be on the outside of the shell,

as in the case of the shell of a submarine subjected to water pressure.

By referring to the derivation of equation (8.2), it is easily veriﬁed that it applies

to such cases provided we follow the conventions:-

(i) The radius R

is always taken to be positive.

(ii) The radius R

is taken to be negative if the two centers of curvature O

are

on the opposite sides of the shell (i.e. if the local region of shell has anticlastic

curvature) and positive if they are on the same side of the shell.

(iii) The pressure p is taken as positive if it acts on the inside surface of the shell

(nearer to the axis) and negative if it acts on the outside surface.

Example 8. 2

Find the circumferential membrane stress

for the conical tank of Figure 8.3 as a

function of height z. Find also the maximum shear stress in the tank.

For the conical tank, we have R

= ∞, since a side view of the cone exhibits

straight sides. To determine R

, we draw a normal to the shell surface at height z as

shown in Figure 8.14, and extend it until it cuts the axis of symmetry.

shell wall

Figure 8.14

From the geometry of this ﬁgure, we note that the cross-sectional radius

r = ztan

8.2 The circumferential stress 397

and hence

cos

ztan

cos

We also note that the internal pressure at height z is

p =

g(h −z) .

Using these values in equation (8.2), we have

cos

ztan

∞

g(h −z)

and hence

g(h −z)ztan

t cos

It follows that the maximum value of

occurs at z=h/2 and is

max

tan

4t cos

which is greater than the maximum meridional stress

max

tan

16t cos

found in §8.1 above.

In this example, R

=∞ and hence

does not enter into the equation. However,

in general, we have to ﬁnd

ﬁrst by the method of §8.1, so that it can be eliminated

in equation (8.2) to determine

The maximum shear stress at any given point in the shell is the largest of



−



−



−



where

are the three principal stresses (see §2.1.2). In membrane stress

problems,

are the two membrane stresses and

is the stress on the local

tangent plane to the shell. This generally varies through the shell thickness, since

one side is loaded by ﬂuid pressure, whilst the other is traction-free. However, the

fact that the shell is thin-walled guarantees that |

|≪|

|,|

|. For example, in

computing

, the pressure force acting over the area

is resisted by the force

due to

acting over the area 2

rt, showing that

is greater than p in the ratio of

at least r/2t. We can therefore approximate

as zero in computing the maximum

shear stress.

In the present example, both membrane stresses are everywhere tensile, so the

maximum shear stress is

max

max(

) −0

The maximum membrane stress is

max

(see above) and hence

max

tan

8t cos

398 8 Membrane Stresses in Axisymmetric Shells

8.3 Self-weight

So far, we have neglected the weight of the shell itself, which is usually a reasonable

approximation for thin-walled shells subjected to pressure loading. However, there

are cases (notably in civil engineering applications) where a signiﬁcant part of the

loading is associated with the self-weight of the structure.

The meridional stress

is determined exactly as in §8.1, except that the weight

of the shell is included as an additional term in the equilibrium equation. In this

calculation, it is sometimes useful to note that the volume of material in a shell of

uniform thickness is approximately equal to the product of the mean surface area of

the shell and the thickness.

ρgt per unit area

Figure 8.15: Self-weight of the shell has a component equivalent to an additional

pressure

The self-weight of the shell also plays a rˆole in the determination of the circum-

ferential stress

, since, in general, it has a component in the direction normal to

the shell and hence modiﬁes equation (8.2). For example, the small element of shell

shown in Figure 8.15 is subject to a gravitational force of

gt per unit area, where

t is the local thickness. This force has a component

gt sin

in the direction of the

outward normal n, and hence has the same effect as an additional internal pressure

of magnitude

gt sin

, where

is the angle between the local tangent to the shell

and the vertical, as shown in Figure 8.15. It is important to check the direction of this

component to make sure whether the resolved component is in the direction of the

outward or the inward normal to the shell, since this will determine the sign of the

additional term in equation (8.2).

Example 8. 3

Figure 8.16 shows a spherical roof shell of mean radius a and uniform thickness t,

loaded only by its own weight. Find the membrane stresses as functions of the polar

angle

if the material has density

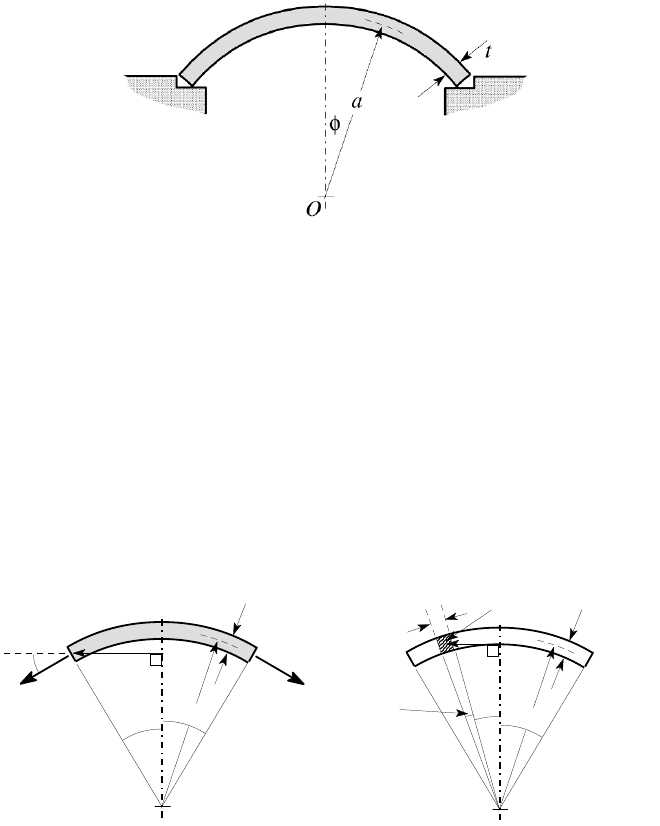
8.3 Self-weight 399

Figure 8.16: Spherical roof shell

To determine

, we cut out the section of shell above the polar angle

, illus-

trated in Figure 8.17 (a). The cross-sectional radius r is then

r = asin

and the meridional stress acts on the area of the cut through the shell thickness, which

is 2

rt (the product of circumference and thickness). Axial equilibrium therefore

requires that

rt)sin

+W = 2

πσ

at sin

+W = 0 ,

where W is the weight of the shell segment and the factor sin

in the ﬁrst term is

required to resolve the force due to

into the vertical direction.

dθ

a dθ

at dθ

(a) (b)

Figure 8.17

To ﬁnd the weight W we need to perform an integration. We ﬁrst note that a

small angle d

at the centre of the sphere corresponds to a segment of shell of length

, as shown in Figure 8.17 (b). This in turn deﬁnes an annular ring of material of

radius r=a sin

and cross-sectional area atd

, shown shaded in Figure 8.17 (b). The

weight of this ring is

dW = 2

ratd

θρ

g = 2

πρ

t sin

400 8 Membrane Stresses in Axisymmetric Shells

and the total weight W is obtained by summing such rings by integration, with the

result

W =

dW = 2

sin

= 2

t(1 −cos

) .

Substituting this result into the equilibrium equation, we then have

πσ

at sin

+ 2

t(1 −cos

) = 0

and hence

= −

ga(1 −cos

)

sin

= −

(1 + cos

)

since sin

=1−cos

. Notice that

is compressive, as we should expect, and that

it is bounded at the top,

= 0, where

=−

ga/2.

The circumferential stress

can be determined from equation (8.2). In the

present case there is no internal pressure p, but as in Figure 8.15, the self-weight,

gt per unit area has a component along the local normal to the shell. The direction

of this force is shown in Figure 8.18 and it has a component along the inward nor-

mal of

gt cos

. This simulates an external pressure, which is treated as negative,

following the conventions of §8.2.2.

ρgt per unit area

Figure 8.18

For the sphere, the two radii are R

=a, so equation (8.2) takes the form

= −

gt cos

from which

= −

ga cos

−



−cos

(1 + cos

)





1 −cos

−cos

1 + cos



It follows that

also tends to −

ga/2 as

→0. In fact, we shall always ﬁnd

that

at any point where a shell crosses the axis of symmetry without a dis-

continuity in slope

or a concentrated force.

An axisymmetric shell with slope continuity must be locally spherical at a point where it

crosses the axis, since all diameters at this point are equivalent.

8.4 Relative magnitudes of different loads 401

The circumferential stress

is compressive near

= 0, but becomes tensile if

cos

+ cos

< 1, which corresponds to the range

> 51.8

. This is a factor of

importance if the shell is to be constructed from a material like concrete, which has

a higher strength in compression than in tension.

8.4 Relative magnitudes of different loads

In the preceding sections, we have considered examples of shells loaded by internal

pressure, the weight of the contents and the self-weight of the shell. In many practi-

cal applications, all these forms of loading will be present, but usually the membrane

stresses will be dominated by one of them and the others can conveniently be ne-

glected, as discussed in §1.3.

The weight of a contained ﬂuid causes the pressure to increase with depth, so that

at depth h, p =

gh. If the surface of the ﬂuid is exposed to atmospheric pressure,

the weight of the contents are therefore responsible for the principal pressure load-

ing of the structure and must be included in the analysis. However, in some cases a

vessel may contain a liquid above which there is a gas (usually vapour) at above at-

mospheric pressure. A typical example is a boiler delivering pressurized steam. The

loading from the gas pressure will usually be signiﬁcantly larger than that from the

weight of the ﬂuid, which can therefore be neglected. To test whether this approxi-

mation is legitimate, calculate the maximum pressure change

gh, between the top

and bottom of the contained ﬂuid and compare it with the gas pressure.

Example 8. 4

A spherical boiler of diameter 6 ft is full to the 4 ft mark with water and delivers

steam at a pressure of 200 psi. Is it necessary to include the weight of the water in a

membrane stress calculation? The density of water is 60 lb/ft

The head of water between the bottom of the boiler and the water surface is

gh =

60 ×4 ×12

= 1.67 psi .

This is less than 1% of the steam pressure (200 psi), so the weight of the water can

reasonably be neglected.

A shell is by deﬁnition thin and hence the volume of shell material is orders

of magnitude smaller than that of the contained volume. It follows that the self-

weight of the shell will be signiﬁcantly smaller than that of any liquid contents,

even allowing for the fact that the shell material will typically have a density several

times larger than that of the contents. After all, a full saucepan or water bottle is

considerably heavier than an empty one. We have seen that the pressure due to ﬂuid

weight is

gh. In view of equation (8.2), this leads to membrane stresses of the order

gha/t, where a is a representative shell radius.

By contrast, the self-weight of the shell will typically yield stresses of the order

gl, where

is the density of the shell material and l is a representative shell

402 8 Membrane Stresses in Axisymmetric Shells

dimension. The results of the preceding examples conﬁrm this general behaviour.

For the conical shell with a contained ﬂuid, we obtained

max

tan

16t cos

;

max

tan

4t cos

both of which contain the factor

/t (since for the cone, radius a is proportional

to height h). The spherical roof shell of Example 8.3 yields the membrane stresses

= −

(1 + cos

)

;



1 −cos

−cos

1 + cos



both of which contain the factor

ga, where a is the radius of the sphere.

In view of these considerations, shell self-weight can almost always be neglected

when there is a contained liquid, but this hypothesis can always be tested in particular

cases by comparing representative estimates of

gl and

gha/t. A similar compar-

ison can be made when a heavy shell is subjected to pressure loading p, using pa/t

as a representative membrane stress.

Example 8. 5

A concrete chimney of height 20 m, mean radius 0.8 m and wall thickness 100 mm is

subject to a maximum pressure difference between inside and outside of 0.05 atm (5

KPa). The density of concrete is 2300 kg/m

. Can either of the two forms of loading

be neglected in a membrane stress calculation?

We compute

5 ×10

×0.8

0.1

= 40 ×10

gh = 2300 ×9.81 ×20 = 450 ×10

and conclude that in this case the loading from self-weight is dominant, at least near

the base of the chimney, so the pressure loading can reasonably be neglected, as long

as a 10% error is acceptable.

8.5 Strains and Displacements

Once the stresses are known, the strains and hence the deformation of the shell can

be calculated. However, the predicted displacements may be constrained either by

a support or by a point of connection between two segments of shell with different

radii. In such cases, the shell experiences local bending.

Since the shell is axisymmetric, only radial and axial displacements are possible.

Axial displacements u

are seldom of importance unless the change in contained

volume in the shell due to internal pressure is required or the shell is prevented by

the support system from axial expansion or contraction. The existence of a radial

8.5 Strains and Displacements 403

displacement u

implies that the local diameter and hence the local circumference

of the shell has increased, as shown in Figure 8.19. It follows that there must be a

circumferential (hoop) strain e

θθ

or e

. In the undeformed view, the radius in the

cross section is r. After deformation, it is r+u

, since all points move a distance u

outwards. Hence, the new circumference is 2

+r) and the circumferential strain

+ r) −2

. (8.3)

But, by Hooke’s law,

−

νσ

(8.4)

and hence

(

−

νσ

. (8.5)

before deformation

after deformation

r +

Figure 8.19: Circumferential strain due to radial displacement u

Example 8. 6

A spherical tank has mean radius 1 m, wall thickness 5 mm, and is made of steel for

which E = 210 GPa,

= 0.3. It is completely full of water at atmospheric pressure.

An additional 0.01 m

of water is then forced into the tank under pressure. Find

the resulting internal pressure if the water can be treated as incompressible and the

weight of the water and the tank can be neglected.

Suppose the ﬁnal internal pressure in the tank is p. Cutting the tank on a diameter,

keeping half the water in each half, we can write the equilibrium equation

×1 ×0.005 ×

−

×1

× p = 0

and hence

= 100p .

404 8 Membrane Stresses in Axisymmetric Shells

In view of the symmetry of the sphere, we also have

=100p.

The radial displacement at all points is therefore

(

−

νσ

100p(1 −0.3) ×1

210 ×10

3 ×10

m ,

where p is in Pa. The increase in volume of the tank due to this displacement is

∆

V =

(1 + u

)

−

≈ 4

3 ×10

but we require

∆

V =0.01 m

, so the ﬁnal pressure must be

p =

3 ×10

×0.01

= 2.4 ×10

Pa (2.4 MPa).

8.5.1 Discontinuities

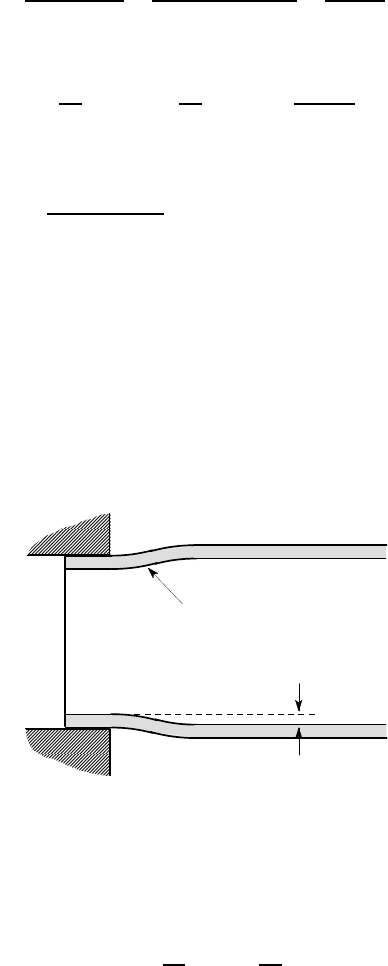
Radial displacements are mainly of concern at the ends of a shell or at points of

discontinuity. For example, suppose a cylindrical shell is built-in to a rigid wall and

subjected to an internal pressure p. Clearly we get a non-zero value for u

, since the

stresses are non-zero, but at the end u

is constrained to be zero. In practice, the shell

will deform as shown in Figure 8.20 and bending stresses will be developed at the

end. We shall show how to determine the transitional shape and the bending stresses

in Chapter 9.

Figure 8.20: Cylindrical pressure vessel built-in to a rigid wall at one end

A less obvious example concerns the cylinder with hemispherical ends and inter-

nal pressure p, shown in Figure 8.21.

In the cylindrical section, the methods of §§8.1, 8.2 give

;

internal pressure p

region of

shell bending