Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

7.5 The particular solution 365

We obtain

u(z) = −

w(z

′

) f

(

|z −z

′

|)dz

′

. (7.38)

Be careful with the absolute value expression |z −z

′

|, particularly when evaluating

the displacement at a point in the range a < z < b. In fact, in this case it is safer to

split the range of integration to make the sign of (z −z

′

) explicit. We then obtain

u(z) = −

w(z

′

) f

[

(z −z

′

)]dz

′

−

w(z

′

) f

[

′

−z)]dz

′

; a < z < b ,

since|z −z

′

|= (z

′

−z) when z

′

>z.

Equation (7.38) deﬁnes a general solution for the displacement of an inﬁnite

beam subjected to a distributed load w(z), but this is not generally the most efﬁ-

cient way of solving such problems, since the integrals tend to be algebraically com-

plicated. Instead, we usually account for a distributed load by seeking a particular

solution of equation (7.5), as will be discussed in the next section.

7.5 The particular solution

If the applied load w(z) is an elementary function, it is usually possible to determine

a particular solution to equation (7.5) by assuming a displacement function u(z) of

similar form. Special cases that can always be solved in this way include polynomial,

trigonometric and exponential functions.

Polynomials

If w(z) is a polynomial of degree n in z, a particular solution can always be obtained

by assuming u(z) to be another polynomial of the same degree, substituting into

equation (7.5) and equating coefﬁcients. For polynomials of degree 3 and below, the

ﬁrst (derivative) term in (7.5) degenerates to zero and we obtain the simple result

u(z) = −

w(z)

. (7.39)

δz

w(z)

w(z )δz

z,z

Figure 7.13: Inﬁnite beam with a distributed load w(z)

366 7 Beams on Elastic Foundations

Trigonometric and exponential functions

If the applied load is of the form w(z) = w

cos(az) [or w

sin(az)], a particular so-

lution can be obtained by assuming u(z) = u

cos(az) [or u

sin(az)] and equating

coefﬁcients. This result is easily extended to more general periodic loading using

Fourier series.

A similar technique can be used for the exponential function w(z)=w

exp(az).

The more advanced reader will recognize that these results open the way to more

general procedures for determining particular solutions, using Fourier or Laplace

transforms.

7.5.1 Uniform loading

If a beam is subjected to a uniform load w(z)=w

throughout its length, the particular

solution

u(z) = −

(7.40)

satisﬁes equation (7.5) and corresponds to a state in which the beam simply moves

downwards as a rigid body to compress the support until an equal and opposite dis-

tributed support force is generated. In this case there will be no shear force or bending

moment in the beam and the particular solution will be the complete solution of the

problem if the ends of the beam are free and unloaded.

Equation (7.40) will not be the complete solution if the ends of the beam are

supported or if the load does not extend over the whole length of the beam. In such

cases, the solution is obtained by superposing the homogeneous solution of §7.2 to

correct the boundary conditions at the ends or at the ends of the loaded region.

Example 7. 2

Figure 7.14 shows a semi-inﬁnite beam of ﬂexural rigidity EI supported on an elastic

foundation of modulus k and simply supported at the end z=0. The beam is subjected

to a uniformly distributed load w

per unit length. Find the maximum bending mo-

ment in the beam.

Figure 7.14: Semi-inﬁnite beam with a uniform load w

per unit length, supported at

the end

w per unit length

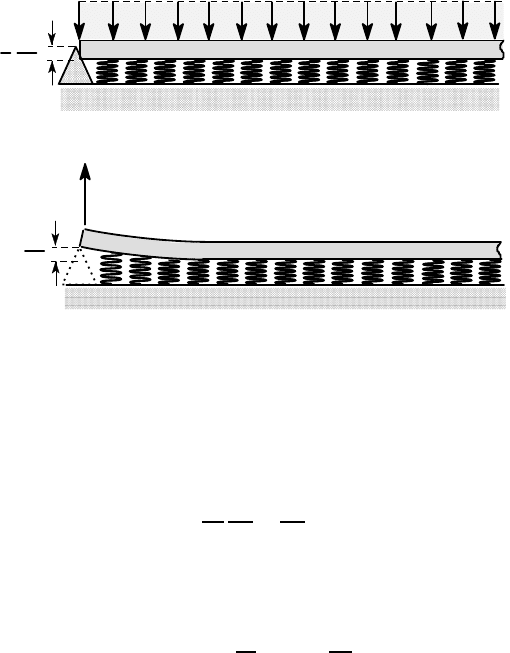
7.5 The particular solution 367

If there were no force at the support, the beam would fall until u(z) = −w

/k,

as in Figure 7.15 (a). To correct the end condition, we must superpose an upward

force F

at z = 0, as in Figure 7.15 (b). The force must be just sufﬁcient to produce

an upward displacement u(0) = w

/k, so as to re-establish contact with the support.

Notice that no moment is applied at the end, since this is a simple support.

(a)

(b)

Figure 7.15: (a) The particular solution, (b) force at the support

In Example 7.1, we found that a downward force F

at the end of a similar semi-

inﬁnite beam produced a displacement u(0)=−2

/k, so having regard to the sign

difference between Figures 7.5 and 7.15 (b), we conclude that

The particular solution produces no bending moment, so the maximum bending

moment is that due to the end force F

which from Example 7.1 is of magnitude

max

| = 0.322

= 0.161

As before, it occurs at the point z=

/4.

7.5.2 Discontinuous loads

If only part of the beam is loaded, we can make a cut in the beam at the discontinuity,

develop a particular solution for each segment and then apply loads to the ends of

each segment sufﬁcient to restore continuity of displacement and slope.

w per unit length

u(z)=

368 7 Beams on Elastic Foundations

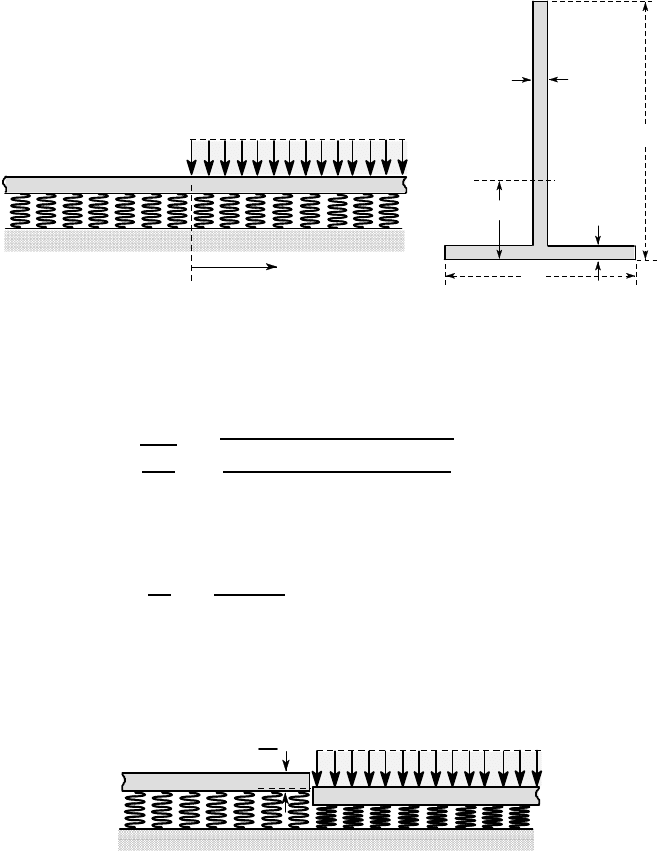
Example 7. 3

A long T-section beam is supported on a Winkler foundation of modulus k =10 MPa

and subjected to a uniformly distributed load w(z) = w

= 50 kN/m in z > 0 only,

as shown in Figure 7.16 (a). The cross section of the beam and the location of the

centroid C are shown in Figure 7.16 (b). The appropriate second moment of area

is I

= 1.17 ×10

−6

and E = 210 GPa. Find the location and magnitude of the

maximum tensile stress in the beam.

110

33.7

all dimensions in mm

(a) (b)

Figure 7.16: (a) Inﬁnite beam with a discontinuous load, (b) cross section of the

beam

We ﬁrst calculate

4EI

10 ×10

4 ×210 ×10

×1.17 ×10

−6

= 1.786 m

−1

Suppose we now make a cut in the beam at z=0, permitting the segment z> 0 to

deﬂect to

u(z) = −

= −

50 ×10

10 ×10

= −5 ×10

−3

m (5 mm downwards).

The segment z < 0, being unloaded, will have no displacement and both beams will

move as rigid bodies, involving no bending moment and no loads on the cut ends.

The displacement produced by this process has the discontinuous form shown in

Figure 7.17.

Figure 7.17: Displacement of the cut beam

w per unit length

7.5 The particular solution 369

We now apply equal and opposite forces and moments to the cut ends of the two

segments, chosen so as to close the gap whilst preserving continuity of slope at z=0.

Since the two segments have similar properties, it is clear that equal and opposite

forces F

will produce equal slopes at the ends, as shown in Figure 7.18.

Figure 7.18: Slopes

for all values of F

Thus, no moments are required at the cut to preserve continuity of slope. Further-

more, the forces produce equal and opposite displacements on the two ends, each of

which must therefore have magnitude w

/2k to restore continuity of displacement.

This is half of the end displacement in the problem of Figure 7.15 (b) and hence the

required force is

= −V (0) =

50 ×10

4 ×1.786

N = 7.0 kN .

No bending moment is generated at z=0. It is a point of inﬂexion in the deformed

beam at which d

u/dz

= 0. The maximum bending moment therefore occurs either

in z > 0 or z < 0. Both beam segments are deformed in a similar manner — the load

in z > 0 merely causes a superposed rigid body displacement as in Figure 7.17.

The maximum bending moment in each segment is therefore the same and, as in

Example 7.1, we have

max

| = 0.322

0.322 ×7

1.786

= 1.25 kNm .

The maximum positive moment occurs at

z = −

= −

= −0.44 m

(in the unloaded segment) and the equal maximum negative moment occurs in the

loaded segment at z=0.44 m.

The bending stresses at the top and bottom of the section at z = −0.44 m in the

unloaded segment are given by

top

max

1.25 ×10

×(110 −33.7)

1.17 ×10

= 81.5 MPa

bottom

= −

1.25 ×10

×33.7

1.17 ×10

= −36.0 MPa .

370 7 Beams on Elastic Foundations

These values are reversed in sign at z = 0.44 m in the loaded segment. We conclude

that the maximum tensile stress occurs in the unloaded segment at the top of the

section and is 81.5 MPa. As a check on the sign convention, we note from Figure

7.18 that the curvature of the beam will place the upper part of the section in tension

on the left and in compression on the right of the discontinuity.

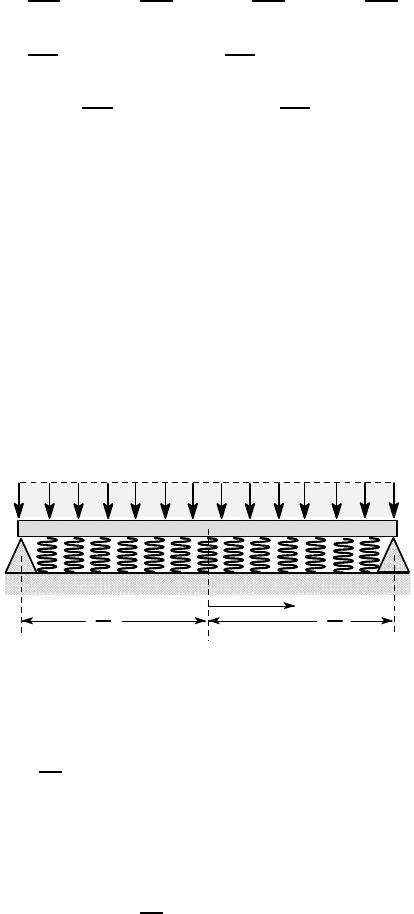
7.6 Finite beams

We argued in §7.3 that in many cases a ﬁnite beam on an elastic foundation can be

treated as semi-inﬁnite because the effects from one end will have decayed before

the other end is reached, leading to essentially uncoupled homogeneous problems for

the conditions at the respective ends. However, this decoupling requires that

L≫1,

where L is the length of the beam. If this condition is not satisﬁed, all four constants

in the homogeneous solution (7.11) must be retained and determined from four si-

multaneous equations, representing the two conditions at each end of the beam.

Figure 7.19: Coordinate system for the ﬁnite beam

In this case, it is generally more efﬁcient to take advantage of the symmetry of

the ﬁnite beam by moving the origin to the mid-point, as shown in Figure 7.19, and

using the hyperbolic form (7.12) of the homogeneous solution, which we here restate

u(z) = C

(

z) +C

(

z) +C

(

z) +C

(

z) , (7.41)

where

(x) = cosh(x)cos(x) ; g

(x) = sinh(x)sin(x) ;

(x) = cosh(x)sin(x) ; g

(x) = sinh(x)cos(x) . (7.42)

Notice that g

are even functions of x and g

are odd functions, so in a sym-

metric or antisymmetric problem, only two of the four arbitrary constants need to be

included. The derivatives of these functions satisfy the relations

= g

−g

;

= g

+ g

;

= g

+ g

;

= g

−g

(7.43)

and

= −2g

;

= 2g

;

= 2g

;

= −2g

. (7.44)

z=L / 2

z=-L /

7.6 Finite beams 371

We can therefore write general expressions for the slope, bending moment and shear

force in the form

(z) = C

(

z) −g

(

z)] +C

(

z) + g

(

z)]

(

z) + g

(

z)] +C

(

z) −g

(

z)] (7.45)

M(z) =

(

z) −

(

z) −

(

z) +

(

z) (7.46)

V (z) =

(

z) + g

(

z)] −

(

z) −g

(

z)]

−

(

z) −g

(

z)] +

(

z) + g

(

z)] . (7.47)

The results are still considerably more algebraically complex than those for long

beams and there is justiﬁcation in practical problems for using the semi-inﬁnite beam

results as an order of magnitude approximation, even for values of

L as low as 3.

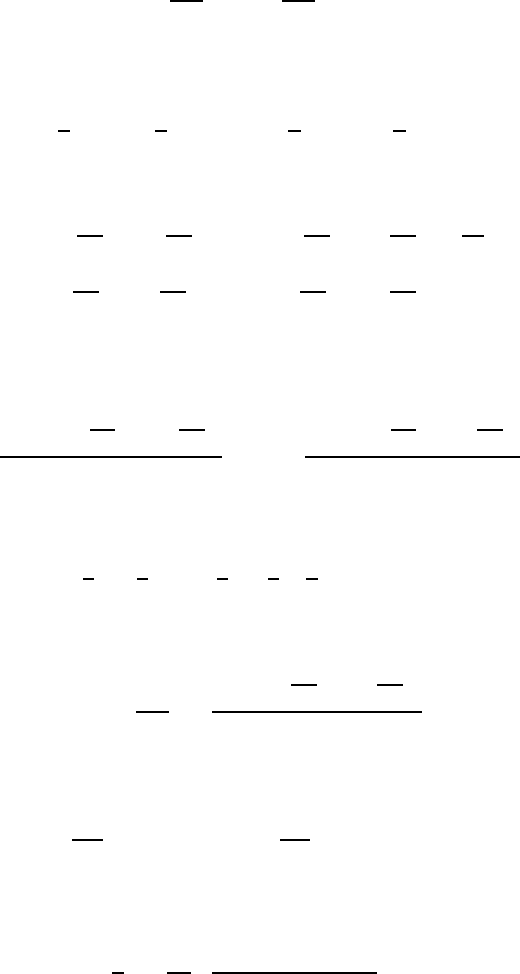
Example 7. 4

A beam of length L and ﬂexural rigidity EI is supported on a foundation of modulus

k and also by two simple supports at the ends. It is loaded by a uniformly distributed

load w

per unit length as shown in Figure 7.20. Find the reactions at the supports

and the bending moment at the mid-point. Show that these results reduce to those

for a simply-supported beam with no elastic foundation when the beam is sufﬁciently

short.

We construct the solution as the sum of the particular solution (7.40) and the

homogeneous solution (7.41), i.e.

u(z) = −

(

z) +C

(

z) +C

(

z) +C

(

z) .

However, the problem is symmetric about the origin and hence the solution must

satisfy the condition u(z)= u(−z), which requires that the constants C

= 0.

We therefore have

u(z) = −

(

z) +C

(

w per unit length

Figure 7.20

372 7 Beams on Elastic Foundations

and

M(z) =

(

z) −

(

z) ,

from (7.47).

The end conditions require





= u



−



= 0 ; M





= M



−



= 0

and hence

cosh





cos





sinh





sin





sinh





sin





−C

cosh





cos





= 0 ,

using the deﬁnitions (7.42).

The solution of these simultaneous equations is

cosh





cos





cosh(

L) + cos(

; C

sinh





sin





cosh(

L) + cos(

where we have used the identity

cosh

cos

+ sinh

sin

(coshx + cosx) .

The bending moment at the mid-point (z=0) is

M(0) = −

= −

sinh





sin





cosh(

L) + cos(

For the support reactions, we ﬁrst note that

V (z) =

(

z) + g

(

−

(

z) −g

(

from (7.47). Substituting for C

, using the deﬁnitions (7.42) and setting z = L/2

we have, after some simpliﬁcation,







sinh(

L) + sin(

cosh(

L) + cos(



which is also the upward force at the support.

7.7 Short beams 373

In the limit

L≪1,

sinh(

L),sin(

L) →

L ; cosh(

L),cos(

L) → 1 ;

sinh





, sin





→

and we obtain

M(0) → −





= −





→

(2)

Both these results agree with the elementary bending theory for a beam on simple

supports with a uniformly distributed load. The elementary theory provides quite

a good approximation up to values of

L that are not strictly small. For example,

with

L = 1, the exact solution gives M(0) = −0.120w

which differs from the

elementary prediction by only 5%.

7.7 Short beams

We saw in the preceding example that when

L ≪1, the solution reduced to that

predicted by the elementary bending theory. In effect, the elastic deformations asso-

ciated with bending were very small and the corresponding support forces generated

by the foundation were negligible.

This will always be the case for a sufﬁciently short beam on an elastic foundation

if it is also kinematically supported, i.e. if there are rigid discrete supports at the ends

or elsewhere, sufﬁcient to prevent rigid body motion if the elastic foundation were

removed. The solution is then very simple. Once we have veriﬁed that the beam

parameters satisfy

the condition

L ≪1, we just ignore the elastic foundation and

solve the remaining conventional beam problem.

If the beam is not kinematically supported, but still satisﬁes the condition

L ≪

1, the foundation forces can be determined by assuming that the beam translates

vertically and rotates as a rigid body. The unknown parameters deﬁning this rigid

body motion are then found by requiring that the complete beam be in equilibrium.

An important special case concerns beam-like structures ﬂoating on the surface

of a liquid.

For practical purposes,

L <1 is generally sufﬁcient to ensure that the approximation will

be sufﬁciently accurate.

374 7 Beams on Elastic Foundations

Example 7. 5

Figure 7.21(a) shows a uniform rectangular beam of length L and weight W ﬂoating

on the surface of a liquid and loaded by a concentrated force F. Assuming that the

beam is short (

L ≪1), ﬁnd the maximum bending moment in the beam. How large

a force F is required to cause one end of the beam to lift out of the liquid.

(a) (b)

Figure 7.21

We ﬁrst treat the beam as a rigid body, in which case its displacement must be a

linear function of z — i.e.

u(z) = A + Bz ,

where A,B are unknown constants. Figure 7.21 (b) shows the displaced conﬁguration

of the beam under load.

It follows that the buoyancy force must be

p(z) = k(A + Bz) ,

where k is a constant. If the beam is to be in equilibrium, we must have

F +W +

p(z)dz = 0 ;

W L

zp(z)dz = 0 ,

where we follow the convention of deﬁning u(z) positive upwards and hence p(z)

positive downwards [see Figure 7.3 (a)]. Substituting for p(z) and evaluating the

integrals, we obtain

kAL +

kBL

= −F −W ;

kAL

kBL

= −

−

W L

with solution

A = −

2kL

−

; B =

and

p(z) = −



−



−

The beam will lift from the liquid if the predicted value of p > 0 and this will

occur ﬁrst at z=L if F > 2W .