Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

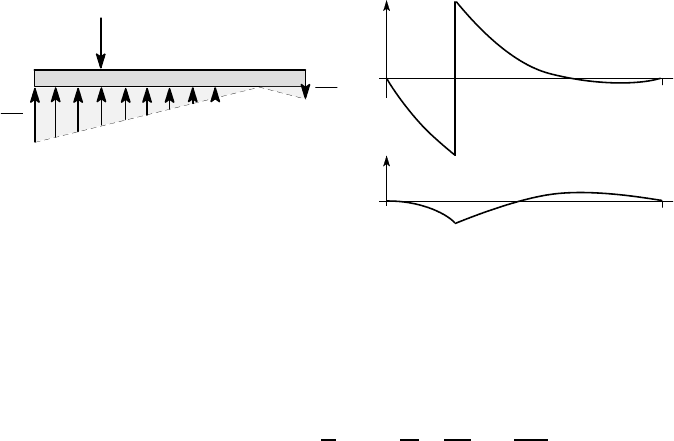
7.8 Summary 375

The last term (−W /L) in the expression for p(z) simply cancels the self-weight

w(z) =W/L and hence makes no contribution to the bending moment in the beam.

The remaining loads are shown in Figure 7.22 (a) and we can sketch the shear force

and bending moment diagrams as in Figure 7.22 (b).

(a) (b)

Figure 7.22

It is clear from the bending moment diagram that the maximum bending moment

will occur under the load at z=L/4 and is

max

| =

L/4

zp(z)dz =

L/4



−



7.8 Summary

In this chapter, we have considered problems in which a loaded beam is supported

by an elastic foundation that provides a restoring force proportional to the local dis-

placement. The theory of beams on elastic foundations has traditionally been used in

civil engineering to model structures and railway tracks on soil foundations. How-

ever, this formalism is also a useful way of describing systems such as thin metal

components bonded to rubber, stiff ﬁbres in a relatively ﬂexible matrix or cartiledge

layers (the foundation) attached to bones (the beam).

The resulting deformation is localized, the displacement decaying exponentially

with distance from the loaded region at a rate which depends upon the foundation

modulus and the ﬂexural rigidity of the beam. The ﬁrst stage in any engineering de-

sign problem of this kind should always be to calculate the decay rate

, since the

nature of the solution depends qualitatively on its relation to the length of the beam

or to the length of the loaded region. The length scale associated with this decay

also provides criteria to assess whether a non-local support or a system of periodic

discrete supports can reasonably be approximated by a uniform local (Winkler) foun-

dation.

376 7 Beams on Elastic Foundations

For continuously loaded beams, the solution can be constructed as the sum of a

particular solution, and a homogeneous solution which describes the localized de-

formation associated with the end conditions. A general particular solution can be

written as an integral [equation (7.38)], but for many practical loading scenarios, the

result is more easily obtained directly from the governing differential equation (7.5).

For long beams, where

L≫1, the load is predominantly carried by the founda-

tion and bending effects are important only in a region near the supports or a discon-

tinuity in loading. The problem is then conveniently treated by ﬁnding a particular

solution for similar loading of an inﬁnite beam and then correcting for the conditions

at each end separately, using the results for the end loading of an otherwise unloaded

semi-inﬁnite beam (7.11).

For short beams (

L ≪1) the foundation has little inﬂuence on the deformation

if the beam is kinematically supported. Otherwise, the beam compresses the founda-

tion essentially as a rigid body and the arbitrary constant(s) deﬁning this rigid-body

motion can be determined from kinematic and equilibrium arguments.

For design purposes, reasonable accuracy can be expected using the long beam

approximation for

L > 3 and the short beam approximation for

L < 1. For beams

of intermediate length, there is interaction between the conditions at the two ends

of the beam, requiring the solution of four simultaneous equations, though some

simpliﬁcation can often be achieved by locating the origin of coordinates at the mid-

point of the beam and using symmetry.

Further reading

A.P. Boresi, R.J. Schmidt, and O.M. Sidebottom (1993), Advanced Mechanics of

Materials, John Wiley, New York, 5th edn., §§10.1–10.6.

R.D. Cook and W.C. Young (1985), Advanced Mechanics of Materials, Macmillan,

New York, §§5.1–5.6.

A.C. Ugural and S.K. Fenster (1995), Advanced Strength and Applied Elasticity,

Prentice-Hall, Eaglewood Cliffs, NJ, 3rd edn., Chapter 9.

Problems

Sections 7.1–7.4

7.1. A semi-inﬁnite beam of ﬂexural rigidity EI is supported on an elastic foundation

of modulus k and simply supported at the end. A moment M

is applied to the beam

at the support. Find the reaction induced at the support and the slope at the end.

7.2. A semi-inﬁnite steel beam of second moment of area I = 5×10

is sup-

ported on an elastic foundation of modulus k = 10 MPa and loaded by a moment of

20 kNm at the end. Find the slope and deﬂection at the end (E

steel

= 210 GPa).

Problems 377

7.3. A long steel I-beam of second moment of area I

= 1.2×10

is supported

on an elastic foundation of modulus 1.2 MPa. Find the force required to deﬂect the

end of the beam by 5 mm (E

steel

=210 GPa).

7.4. A long steel I-beam of second moment of area I

=3.0×10

is supported on

an elastic foundation of modulus 4.0 MPa. An end force is applied so as to cause an

end deﬂection of 2 mm. Find the force required and the resulting maximum bending

moment in the beam (E

steel

=210 GPa).

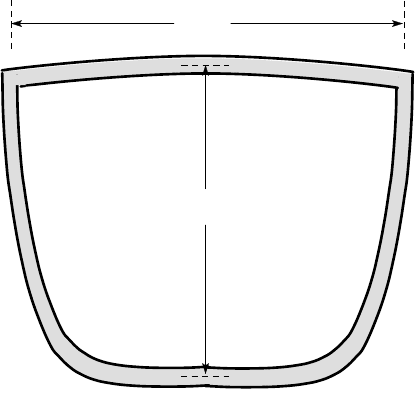
7.5. Figure P7.5 shows the cross section of an oil tanker. Obtain an order of mag-

nitude estimate of the ﬂexural rigidity of the section by approximating it by a 70

ft diameter hollow cylinder with a 2 inch thick steel wall (E = 30×10

psi). Hence

estimate the decay length l

for the tanker, considered as a beam on an elastic foun-

dation. Would a typical tanker be ‘long’or ‘short’ according to the criteria of §7.3?

The density of sea water is 62 lbs/ft

70 ft

65 ft

Figure P7.5

7.6. Figure P7.6 shows the cross section of a semi-inﬁnite C254×45 steel channel

which rests on an elastic foundation of modulus k = 10 MPa and is loaded by a

downward force of 20 kN at the end. The second moment of area of the channel

for bending about the horizontal axis is I

= 1.64×10

and the centroid C is

located at a distance 18 mm from the bottom of the section. Find the deﬂection at the

free end and the location and magnitude of the maximum tensile stress in the beam.

steel

=210 GPa)

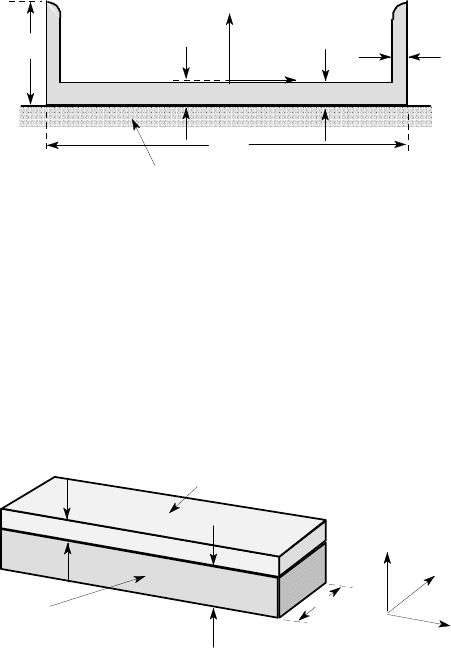
Figure P7.7

7.8. An inﬁnite beam on an elastic foundation is loaded by a concentrated force F

What will be the percentage error in the predictions of (i) the maximum deﬂection

and (ii) the maximum bending moment, if the modulus k of the foundation is over-

estimated by 50%?

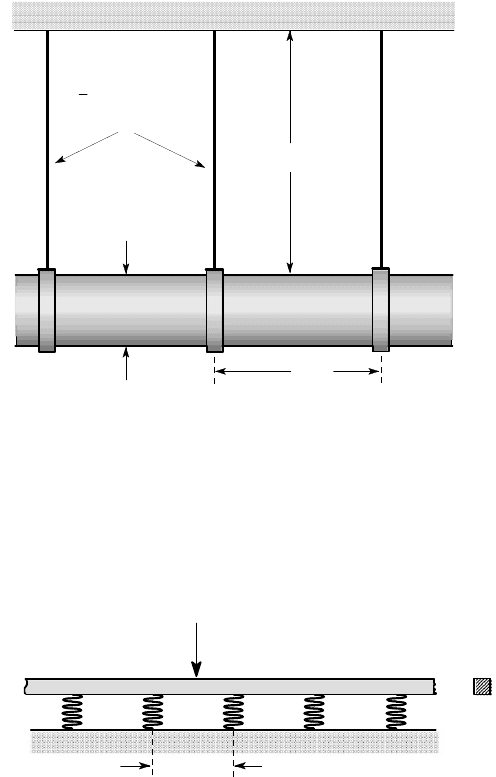
7.9. An air duct consists of an aluminium thin-walled tube of diameter 1 ft and wall

thickness 1/8 in. It is supported by a set of steel cables of diameter 1/8 in and length

4 feet, with an axial spacing of 3 feet, as shown in Figure P7.9. Find the characteristic

length l

for this system and comment on whether it can reasonably be analyzed as a

beam on an elastic foundation (E

steel

=30×10

psi, E

aluminium

=11×10

psi).

378 7 Beams on Elastic Foundations

17.1

11.1

254

Elastic foundation

all dimensions in mm

Figure P7.6

7.7. A mounting assembly involves a 2 mm steel strip bonded to a 4 mm rubber

layer, which in turn is supported by a rigid base, as shown in Figure P7.7. Estimate

the modulus of the rubber foundation, assuming that the out-of-plane stress

always zero. Hence, estimate the decay length l

for the assembly, considered as a

steel beam on a rubber foundation (E

rubber

=1.4 MPa,

rubber

=0.5, E

steel

=210 GPa,

steel

=0.3).

rubber

steel

all dimensions in mm

Problems 379

7.10. Figure P7.10 shows a long steel beam of 80×80 mm square cross section

supported on discrete springs of stiffness 1 kN/mm, spaced 100 mm apart. Can this

support reasonably be considered as an elastic foundation?

The beam is loaded by a force of 20 kN as shown. Find the maximum tensile

stress in the beam and the maximum force carried by any individual spring. (E

steel

210 GPa).

Figure P7.10

7.11. In Problem 7.10 additional springs are provided to reduce the axial spacing to

50 mm, other parameters remaining the same. Find the maximum tensile stress in the

beam and the maximum force carried by any individual spring.

Section 7.5

7.12. An inﬁnite beam of ﬂexural rigidity EI is supported by an elastic foundation of

modulus k and is subject to a sinusoidal load

1 ft

4 ft

3 ft

diameter

cables

Figure P7.9

100 mm

20 kN

80 mm

380 7 Beams on Elastic Foundations

w(z) = w

sin(az) ,

where a is a constant. Find the displacement u and the bending moment M as func-

tions of z and hence show that for a given value of the load amplitude w

, the maxi-

mum bending moment occurs when

a =

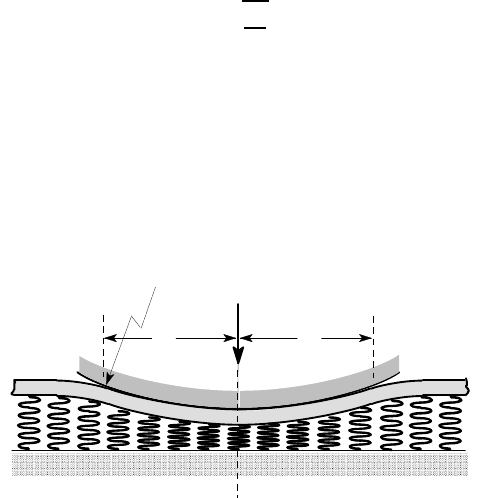
7.13**. A rigid cylinder of large radius R is pressed against an inﬁnite beam of

ﬂexural rigidity EI supported by an elastic foundation of modulus k, as shown in

Figure P7.13. Find an expression for the force F required to establish a contact area

of length 2a in terms of R,

,k,a only. Find also the deﬂection u

at the mid-point

in terms of the same variables and hence obtain the (non-linear) relation between F

and u

What happens at low values of F?

7.14*. An inﬁnite beam of ﬂexural rigidity EI is supported by an elastic foundation

of modulus k and is loaded by a force F

, which is uniformly distributed over the

region −L<z< L — i.e. w(z)= F

/2L in this range.

Find expressions for the displacement and the bending moment as functions of z

(i) in −L <z< L and (ii) in z>L.

Hint: This problem can be solved by integration, using equation (7.38), but an

easier method is to represent the loading as the superposition of (i) a load w(z) =

/2L in −L < z < ∞ and (ii) a negative load w(z) = −F

/2L in L < z < ∞. These

separate problems are both similar to that treated in Example 7.3, except for a change

of origin.

7.15. Write a computer program to locate the maximum bending moment for Prob-

lem 7.14 (by ﬁnding the points where V =0).

Run the program for various values of

L and plot a graph of M

max

as a

function of

L, where M

is the value of M

max

for L = 0 — i.e. M

is the moment

under a concentrated force F

and is given by equation (7.37).

Figure P7.13

7.17. A semi-inﬁnite beam of ﬂexural rigidity EI is supported by an elastic founda-

tion of modulus k and built in at the end, as shown in Figure P7.17. The beam is

subjected to a distributed load

w(z) = w

−az

Find the bending moment at the support in terms of w

,a,

,k only.

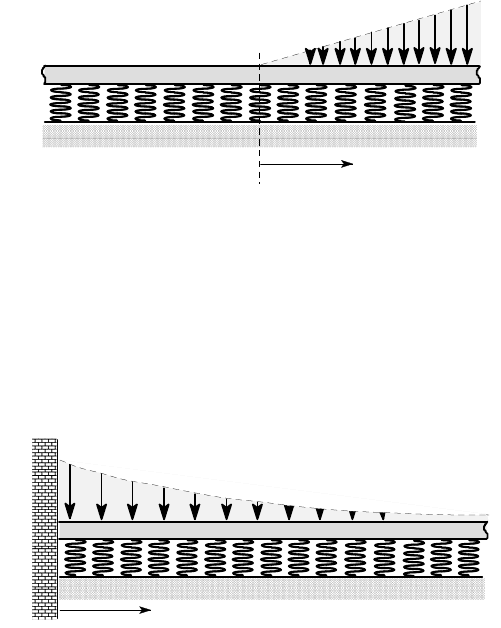
7.18**. An inﬁnite beam of ﬂexural rigidity EI is supported on an elastic foundation

whose modulus is k

in z > 0 and 2k

in z < 0. The beam is subjected to a uniformly

distributed load w

per unit length, as shown in Figure P7.18. Find the location and

magnitude of the maximum bending moment.

w(z)=w exp(az) per unit length

Figure P7.17

Problems 381

Note that there are many places where V = 0, both under the load and in the

unloaded region. Your program must determine at which one the magnitude of the

bending moment is greatest.

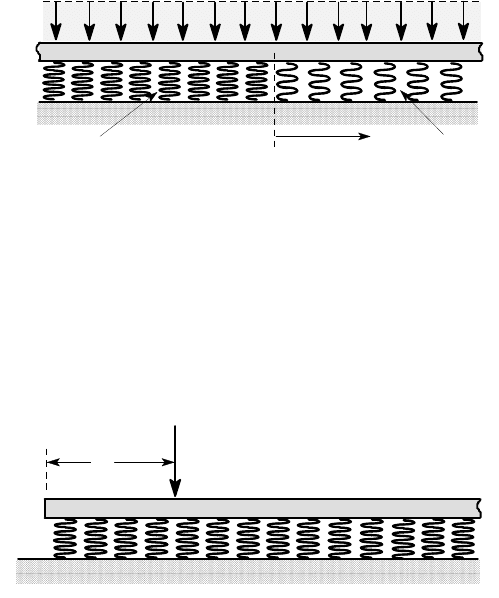
7.16. Figure P7.16 shows an inﬁnite beam of ﬂexural rigidity EI, supported by an

elastic foundation of modulus k and subjected to a linearly varying load

w(z) = w

in z > 0. Find the bending moment in the beam as a function of z. Hence show that

the maximum bending moment occurs at O and ﬁnd its magnitude.

w z per unit length

Figure P7.16

382 7 Beams on Elastic Foundations

Hint: Split the beam at z = 0 and then determine the moment and shear force

needed there to re-establish continuity of slope and deﬂection. Notice however that

takes different values on the two sides, so the problem is not symmetrical, in contrast

to Example 7.3.

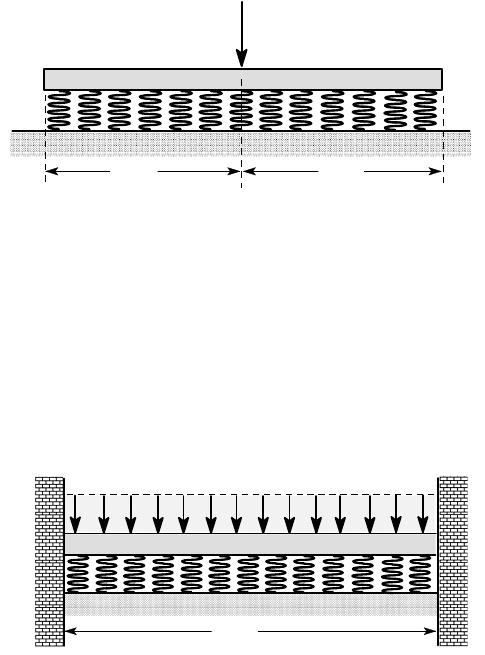
7.19. A semi-inﬁnite beam of ﬂexural rigidity EI is supported by an elastic founda-

tion of modulus k and loaded by a concentrated force F a distance a from the end, as

shown in Figure P7.19. Find the deﬂection under the load, the deﬂection at the end

and the bending moment under the load.

Hint: Use the solution for a force on an inﬁnite beam, make a cut at the point

z= −a and correct for the end conditions.

Sections 7.6, 7.7

7.20. A rectangular wooden plank of width 12 in, thickness 2 in and length 30 ft

ﬂoats on the surface of a lake. The wood has speciﬁc gravity 0.8 and Youngs modulus

E =1.6×10

psi and the density of water is 60 lb/ft

. A man weighing 150 lbs steps

carefully onto the plank at one end. Will he get his feet wet?

7.21. Figure P7.21 shows a ﬁnite beam of ﬂexural rigidity EI loaded by a concen-

trated force F

at the mid-point. The beam is supported on an elastic foundation of

w per unit length

Figure P7.18

Figure P7.19

Problems 383

modulus k, but is otherwise unsupported. Find the displacement and the bending

moment at the mid-point.

7.22. Figure P7.22 shows a beam of length 2 m and ﬂexural rigidity EI = 2×10

, subjected to a uniform load w

= 4 kN/m. The beam is built in at both ends

and supported on an elastic foundation of modulus k = 0.8 MPa. Find the bending

moments at the support and at the mid-point and the maximum deﬂection.

7.23. The oil tanker of Problem 7.5 is 500 feet long and when fully laden it rides in

still water so that the lowest point of the hull is 50 feet below the water line. In a gale,

the tanker has to traverse waves of peak-to-trough height of 18 feet and wavelength

50 feet. Estimate the maximum tensile stress generated in the hull. Will the stresses

be worse when cutting through the waves at right angles, or at an angle?

7.24. A ﬁnite beam of length L and ﬂexural rigidity EI is built in at its ends and

supported on a foundation of modulus k. It is subjected to a uniform load w(z)=w

Find the deﬂection at the centre and the restraining moments at the supports for the

case where

L= 1.

4 kN/m

2 m

Figure P7.22

L /

Figure P7.21

384 7 Beams on Elastic Foundations

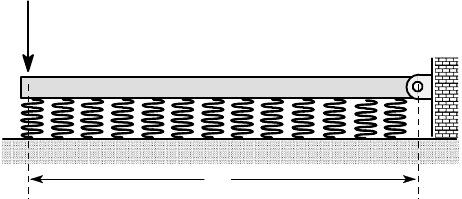
7.25. A beam of length L is pinned at one end and supported on an elastic foundation

of modulus k, such that

L≪1. The beam is loaded by a force F at the end, as shown

in Figure P7.25. Find the location and magnitude of the maximum bending moment

and the deﬂection at the loaded end.

Figure P7.25