Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

Membrane Stresses in Axisymmetric Shells

A shell is any structure or part of a structure in which one local dimension is much

smaller than the other two. Shells abound in all branches of engineering and in the

natural world. Examples include gas tanks, thin-walled pipes and air ducts, grain

hoppers, car bodies, aircraft wings and fuselages, window panes, eggshells, wine-

glasses, concrete roofs and the human skull.

A shell which is plane in the undeformed state is known as a plate. Plates are

generally much less efﬁcient than curved shells as structural elements, being more

ﬂexible and less capable of transmitting transverse loads (i.e. loads normal to the

plane) without failure. You can verify this by pushing against a plate glass window or

the plane side of a metal ﬁling cabinet. You will ﬁnd that it is quite easy to produce an

observable deﬂection. The same material formed into a curved shell (e.g. a car body

panel or a drinking glass) will sustain an equal transverse load without observable

deformation.

The basic idea behind the analysis of shells is that the stresses can’t vary much

across the thin dimension and hence we can approximate the stress distribution

across the thickness by a Taylor series. When the shell is very thin, only the ﬁrst

term of this series will be important — this is the ‘membrane theory’, in which the

stresses are assumed to be uniform through the thickness. In many problems — par-

ticularly those involving shells with discontinuities or built-in boundary conditions

— it is necessary to include both the ﬁrst and second terms of the series. This con-

stitutes the ‘bending theory of shells’.

It might be helpful to draw an analogy with beams, which of course are structures

in which two dimensions are much smaller than the third. The ‘membrane theory of

beams’ assumes that the axial stress

is uniform across the section and hence

corresponds only to the transmission of an axial force passing through the centroid.

The addition of one extra term in the Taylor series permits the stress to vary linearly

across the section and deﬁnes the bending theory of beams.

In this chapter, we shall restrict attention to the membrane theory of shells, which

therefore implies that bending moments are everwhere negligible. It follows that

derivative of the bending moment must also be everywhere negligible and hence

J.R. Barber, Intermediate Mechanics of Materials, Solid Mechanics and Its Applications 175,

2nd ed., DOI 10.1007/978-94-007-0295-0_8, © Springer Science+Business Media B.V. 2011

386 8 Membrane Stresses in Axisymmetric Shells

there can be no shear force or transverse shear stress, by extension of equation (6.1).

In other words, the only non-zero stresses are in the local (tangential) plane of the

shell and are uniform through the thickness.

Despite these restrictions, we shall ﬁnd that the curvature of a membrane shell

permits it to transmit a wider range of loads than either a straight beam or a plate un-

der similar restrictions, making the shell a useful and versatile lightweight structural

member. We shall illustrate this here for the particular case of axisymmetric shells

under axisymmetric loading.

8.1 The meridional stress

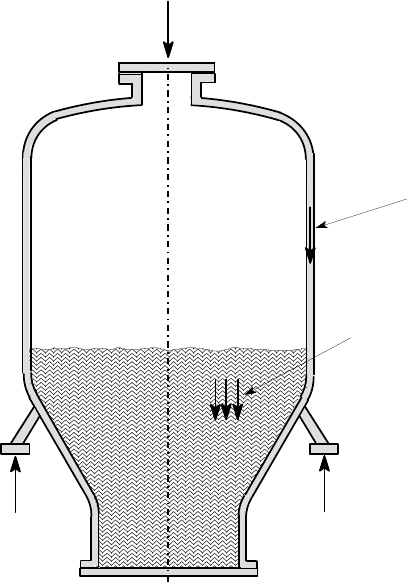
Figure 8.1 shows the cross section of an axisymmetric shell subjected to various

kinds of axisymmetric loads. In particular, the shell may contain a liquid of density

and a gas at pressure p, there may be resultant axial forces F from the attached

ductwork and reactions R at the support, and the density

of the shell material itself

may cause signiﬁcant loading.

gas

pressure

ρ g per unit volume

Figure 8.1: Loading of an axisymmetric shell

8.1 The meridional stress 387

Suppose we now separate the shell into two parts by making a cut perpendicular

to the axis of symmetry. The free body diagram of one such part is shown in Figure

8.2. We anticipate a membrane stress

at the cut as shown. Notice that the cut is

made perpendicular to the shell wall,

so as to expose the membrane stress which is

tangential to the wall.

Figure 8.2: Free body diagram exposing the meridional stress

The segment of shell in Figure 8.2 must be in equilibrium under the action of the

forces shown and we can obtain an equilibrium equation by summing the forces in

the axial direction. If the shell and the applied loads are axisymmetric, the membrane

stress

will be the same all around the cut, so this equation will be sufﬁcient to

determine

, which is known as the meridional stress or the longitudinal stress.

Example 8. 1

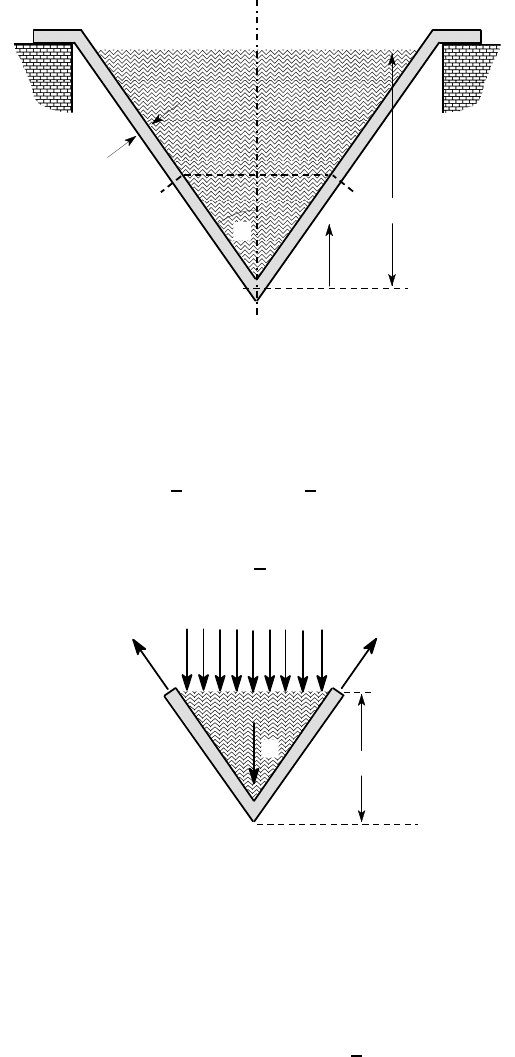
Figure 8.3 shows a conical tank, supported at the top and ﬁlled with water of density

to a height h above the vertex. The cone has semi-angle

and the wall thickness

is t. Find the meridional stress

as a function of z and identify the location and

magnitude of the maximum value. The weight of the shell may be neglected.

To ﬁnd

at height z, we make the cut A−A shown in Figure 8.3, taking care to

go through the shell at right angles. The simplest procedure is to ‘cut’ through the

water as well, leaving the free-body diagram of Figure 8.4. Three forces act on the

system shown in this ﬁgure, resulting from:-

(i) the meridional stress

acting on the cut shell surface;

(ii) the hydrostatic pressure

g(h−z) due to the head of water above A−A acting on

the water surface A−A; and

(iii) the weight W of the cone of water left below A−A and shown in Figure 8.4.

One way to remember this is to imagine actually making the cut with a hacksaw. The cut

to make is the one that requires the least effort, because it goes through the minimum wall

thickness.

Because on a globe regarded as a shell,

would act in the direction of a line of longitude,

also known as a meridian.

388 8 Membrane Stresses in Axisymmetric Shells

Figure 8.3: The conical tank

To determine W , we note that the volume of a cone of height b and base radius a

is V =

b/3. Here, b=z and a =ztan

, giving

V =

(ztan

)

z =

tan

and

W =

gV =

πρ

tan

ρg (h - z)

Figure 8.4: Free-body diagram of the system below the cut A−A

The stress

acts on the area of the cut through the shell wall, which is of

thickness t and circumferential length 2

a = 2

ztan

. Finally, the water pressure

g(h−z) acts over a circular area at A−A of radius a = z tan

whose area is there-

fore

(ztan

)

The three forces must sum to zero and hence

zt tan

)cos

−

g(h −z)

(ztan

)

−

πρ

tan

= 0 , (8.1)

8.1 The meridional stress 389

where the factor cos

in the ﬁrst term results from resolution of the force due to

into the vertical (axial) direction.

Solving this equation for the meridional stress

, we obtain

gztan

2t cos



h −



We note that

is zero at the vertex z = 0 and elsewhere is always positive. The

maximum value occurs when

= 0

which requires

h −

z = 0 or z =

At this point, we have

max

tan

16t cos

8.1.1 Choice of cut

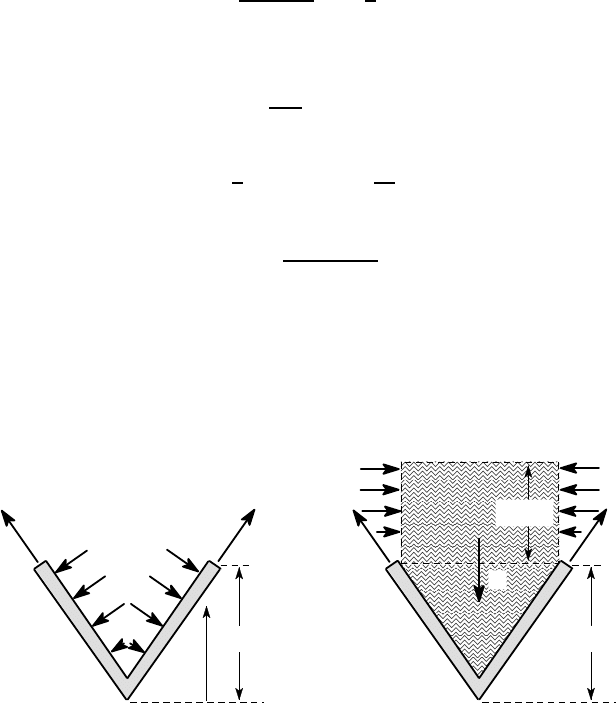
In Example 8.1, we made the cut in such a way as to leave a conical volume of water

in the free-body diagram of Figure 8.4, but any other axisymmetric cut could have

been used, two alternatives being illustrated in Figure 8.5 (a,b).

ρg (h - ζ)

(a) (b)

Figure 8.5: Alternative cuts for determining

In Figure 8.5 (a), we show the shell segment only, implying a cut which passes

between the water and the shell surface. In this case, the pressure exerted by the

water on the shell must be shown, since it results in an external force on the shell

segment. The resultant axial force due to this pressure can be found by considering

the element of shell surface between height

and

δζ

above the vertex, multi-

plying by the local pressure

g(h−

), resolving the resulting elemental force into

(h - z)

390 8 Membrane Stresses in Axisymmetric Shells

the axial direction and summing by integration. The ﬁnal result will be found to be

equal to the sum of terms (ii) and (iii) in the original derivation, but the calculation

is signiﬁcantly more tedious, which is why we used the cut of Figure 8.4.

Another alternative cut, shown in Figure 8.5 (b), passes through the shell and then

goes vertically upwards to the water surface, so as to include an additional cylindri-

cal volume of water above the plane AA in the free-body diagram. This cylinder is

subjected to pressure from the rest of the water acting on the cylindrical surface AB,

but since these forces are horizontal, they do not feature in the vertical equilibrium

equation. Thus, the only two terms in the equilibrum equation are those due to

and to the weight of water in the free-body diagram [(i) and (iii) of the preceding

solution]. However, the weight of water W is now increased by the weight of the

cylinder AB and it is easily veriﬁed that this is equal to the missing term (ii). The

volume of the cylinder is

cyl

(ztan

)

(h −z) ,

so its weight is

cyl

πρ

g(ztan

)

(h −z) ,

which is exactly equal to the second term in the equilibrium equation (8.1).

In general, any axisymmetric cut can be used to determine the meridional stress,

provided it cuts through the shell at only one location. All cuts will yield the same

equilibrium equation, but a careful choice will sometimes simplify the calculations.

A good ‘default option’ is to make a plane cut perpendicular to the axis,

as in Figure

8.4.

The three cuts deﬁned by the free-body diagrams of Figure 8.4 and Figure

8.5 (a,b) yield the same ﬁnal equilibrium equation because the volumes of water

involved — i.e. the conical volume in Figure 8.4 and in the cone and the cylinder

in Figure 8.5 (b) — are themselves in equilibrium under the action of gravity and

pressure forces.

In the limiting case where the density and hence the weight of the contents of a

pressure vessel is negligible, the pressure will be the same everywhere and we can

conclude that the resultant of a uniform pressure acting on a general curved surface

is the same for all surfaces terminating on the same closed curve.

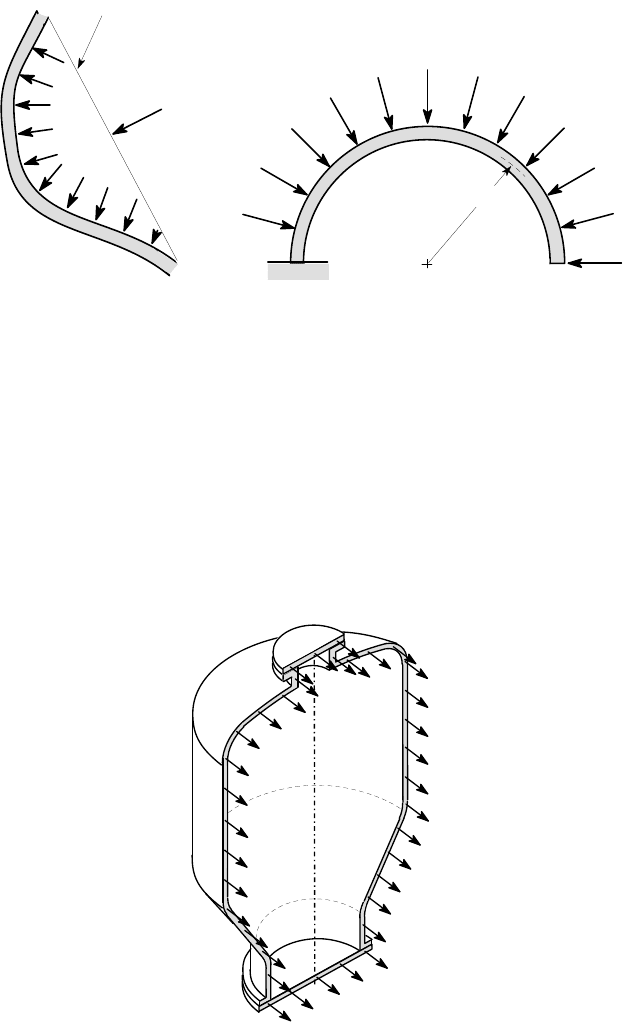
In particular, the uniform pressure p acting on the shell surface of Figure 8.6 (a) is

statically equivalent to a force pA

, where A

is the area of the plane surface A−A and

the line of action of this force passes through the centroid of A

and is perpendicular

to the plane A−A. This result can be useful outside the context of the membrane

theory of shells. For example, we can use it to deduce that the distributed load on the

curved beam of Figure 8.6 (b) is statically equivalent to a vertical force 2w

R acting

through the centre O.

Except in passing through the shell itself, where the cut must be normal to the local shell

surface.

8.2 The circumferential stress 391

area

w per unit length

(a) (b)

Figure 8.6: (a) uniform pressure on a general shell segment, (b) uniform normal

loading on a curved beam

8.2 The circumferential stress

Since the system is axisymmetric, there can be no shear stresses on the meridional

surface and hence

is a principal stress. The other principal stress

in the local

tangent plane to the shell is known as the circumferential stress or the hoop stress.

On a globe, it would act in the direction of a line of lattitude — i.e. in the East-West

direction.

Figure 8.7: The circumferential stress

392 8 Membrane Stresses in Axisymmetric Shells

We can expose

by making any plane cut that includes the axis of symmetry, as

shown in Figure 8.7, but we cannot generally determine it from such a cut because

is not necessarily uniform over the cut surface. However, we can ﬁnd it by con-

sidering the equilibrium in the through-thickness direction of the small rectangular

element of shell shown in Figure 8.8.

δy

δx

Figure 8.8: Equilibrium of a small rectangular element of shell

We suppose that the shell element is loaded only by an internal pressure p, acting

normal to the shell, and the membrane stresses

. The pressure exerts a force

y in the direction normal to the shell. To determine the forces due to

, we

ﬁrst draw edge views of the element looking in directions A, B, as shown in Figure

8.9 (a,b), respectively. In general, the curvature of the shell will be different in the

two views, so we denote the corresponding radii by R

, respectively.

δθ

σ t δy

δθ

δx

δφ

σ t δx

δy

(a) (b)

Figure 8.9: View of the shell element in (a) direction A and (b) direction B

As a result of the curvature, the length

x in Figure 8.9 (a) subtends an angle

δθ

8.2 The circumferential stress 393

at the centre of curvature. The stress

acting on the edges of the element cor-

responds to forces

y on each edge in Figure 8.9 (a) and these forces are not

horizontal in the ﬁgure because of the curvature of the shell. They therefore have

a resultant in the direction normal to the shell (vertically downwards in the ﬁgure)

equal to

y sin



δθ



≈

δθ

The approximation involved in replacing sin(

δθ

/2) by

δθ

/2 will be exact in

the limit

x →0. A similar argument applied to Figure 8.9 (b) shows that the forces

x due to stress

have a resultant in the same direction (normal to the shell) of

Summing the forces along the common normal for the element

y, we there-

fore obtain

− p

y = 0 ,

and hence

. (8.2)

The meridional stress

can always be calculated by using axial equilibrium

arguments, as in §8.1, so equation (8.2) can be used to determine the circumferential

stress

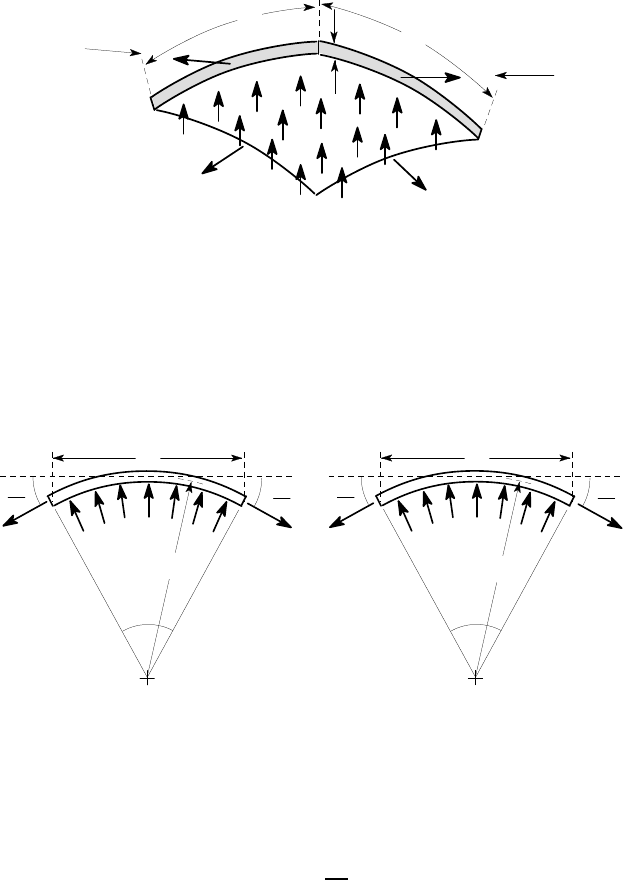
8.2.1 The ra dii of curvature

Notice that the shell element has two radii of curvature

, which appear in

the two orthogonal views on A and B respectively (see Figure 8.9). These radii are

generally different. For example, for the cylindrical shell of Figure 8.10 (a), the cor-

responding element [Figure 8.10 (b)] will appear curved when looking in direction B

along the axis, giving R

=a. However, it will look straight when looking in direction

A, so R

=∞.

Even a general (non-axisymmetric) element of shell has two orthogonal principal curva-

tures and corresponding principal radii R

. This can be established by a transformation

of coordinates mathematically analogous to those used in §2.1.1 and §4.4.1. For the ax-

isymmetric shell, the principal directions must always align with the circumferential and

axial directions.

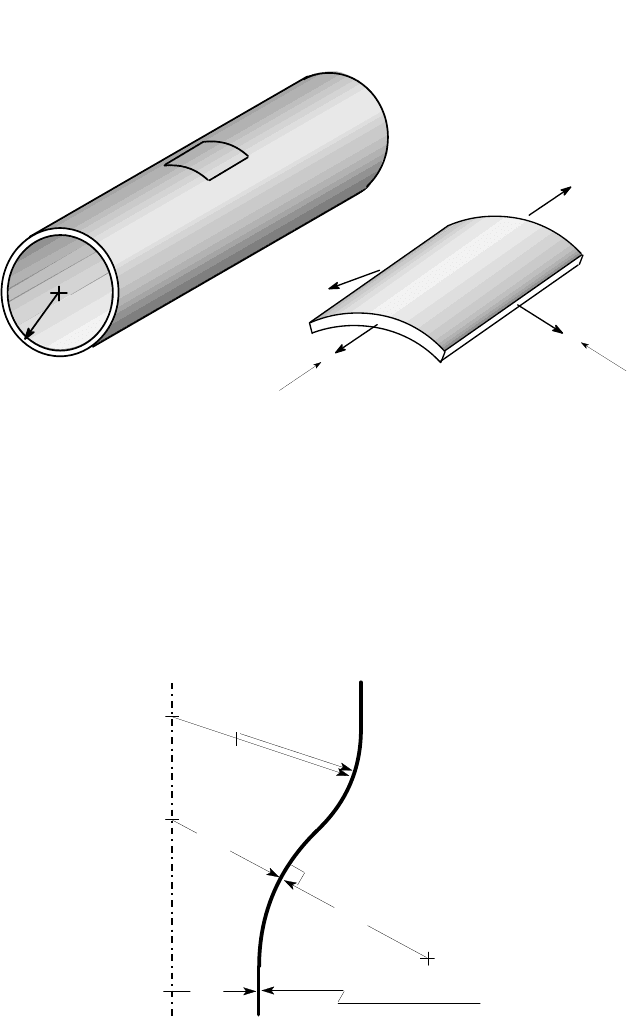
394 8 Membrane Stresses in Axisymmetric Shells

(a) (b)

Figure 8.10: (a) A cylindrical shell and (b) the corresponding rectangular shell ele-

ment

More generally, the radius R

is that which is seen in a cross-sectional view of

an axisymmetric shell — i.e. when the shell is sectioned on a plane including the

axis of symmetry. To determine the other radius R

, we ﬁrst note that both centres

of curvature must lie on the common normal to the local piece of shell. Also, the

axisymmetry demands that the centre O

must lie on the axis of symmetry. To ﬁnd

and hence R

, we therefore extend the normal until it cuts the axis, as shown for

various cases in Figure 8.11.

Figure 8.11: Radii of curvature for the shell

Take care not to confuse R

with the local cross-sectional radius r, shown in

Figure 8.12 (a). In determining the meridional stress, r will be the radius of the cross-