Barber J.R. Intermediate Mechanics of Materials
Подождите немного. Документ загружается.


7.1 The governing equation 355
V(z)
V(z+δz)
M(z)
M(z+δz)
p(z)δz
w(z)δz
δz
(b)
Figure 7.3: (a) A beam supported on a Winkler foundation, (b) equilibrium of a beam
element
Equilibrium of vertical forces therefore requires that the shear force V satsify the
equation
V (z +
δ
z) −V(z) −w(z)
δ
z − p(z)
δ
z = 0
and hence
V (z +
δ
z) −V (z)
δ
z
= w(z)+ p(z) .
Allowing
δ
z →0 and using (7.1), we then obtain
dV
dz
= w(z)+ p(z) = w(z)+ ku(z) . (7.2)
As in §6.1, moment equilibrium requires
dM
dz
= V (7.3)
and the bending moment M and the displacement u are related by the bending equa-
tion (1.17)
M = −EI
d
2
u
dz
2
. (7.4)
Eliminating M,V between equations (7.2–7.4), we obtain
EI
d
4
u
dz
4
+ ku = −w , (7.5)
which is the governing equation for an elastic beam supported by a Winkler founda-
tion.
7.1.1 Solution of the governing equation
The applied load w will generally be a known function of z and hence (7.5) consti-
tutes an inhomogeneous ordinary differential equation for the unknown displacement
u(z). Once this equation is solved, the bending moment can be recovered by substi-
tution in (7.4).
beam
u(z)
w(z) per unit length
z
(a)

356 7 Beams on Elastic Foundations
The general solution of (7.5) can be written as the sum of a particular solution
and the general homogeneous solution. The particular solution is any function that
satisfies (7.5) and the homogeneous solution is the general solution of the corre-
sponding homogeneous equation
EI
d
4
u
dz
4
+ ku = 0 . (7.6)
Since (7.6) is a fourth order equation, its solution will contain four arbitrary constants
which permit the satisfaction of two boundary conditions at each end of the beam, as
in elementary beam problems.
The particular solution and the homogeneous solution can be given a physical in-
terpretation. The particular solution corresponds to a state in which the correct load
w(z) is applied, without regard to the end conditions, which will therefore gener-
ally not be those required in the problem. Hence, we must superpose forces and/or
moments at the ends so as to restore the correct end conditions. This is the func-
tion of the general homogeneous solution, which describes all possible states of the
same beam loaded at the ends only — after all, (7.6) is simply (7.5) with w(z) equal
to zero. We shall first examine the homogeneous solution in some detail, since it
affords considerable insight into the general behaviour of beams on elastic founda-
tions. In particular, we shall find that the deformation tends to be quite localized near
the loads, in contrast to the behaviour of beams on discrete supports.
7.2 The homogeneous solution
If the beam has no distributed load w(z), the displacement is given by equation (7.6),
whose form suggests the existence of solutions of the form
u(z) = Ae
bz
, (7.7)
where A,b are constants. Substitution into (7.6) yields
EIb
4
Ae
bz
+ kAe
bz
= 0 ,
showing that (7.7) will be a solution of (7.6) if and only if
b
4
= −
k
EI
. (7.8)
This equation has no real roots, but it has four complex roots which can be written
b = (±1 ±i)
β
,
where
β
=
4
r
k
4EI
. (7.9)
This solution is easily verified by substitution back into (7.8).

7.2 The homogeneous solution 357
It follows that the general solution of the homogeneous equation (7.6) can be
written
u(z) = A
1
e
(1+i)
β
z
+ A
2
e
(1−i)
β
z
+ A
3
e
(−1+i)
β
z
+ A
4
e
(−1−i)
β
z
, (7.10)
where A
1
,A
2
,A
3
,A
4
are four independent complex constants. However, the displace-
ment must be a real function, so we must have A
2
=
¯
A
1
,A
4
=
¯
A
3
, where the overbar
denotes the complex conjugate. After some algebraic manipulations, the most gen-
eral real function of the form (7.10) can be written
u(z) = B
1
e
β
z
cos(
β
z) + B
2
e
β
z
sin(
β
z) + B
3
e
−
β
z
cos(
β
z) + B
4
e
−
β
z
sin(
β
z) . (7.11)
An alternative form which is sometimes more convenient for beams of finite length
is
u(z) = C
1
cosh(
β
z)cos(
β
z) +C
2
sinh(
β
z)sin(
β
z) +C
3
cosh(
β
z)sin(
β
z)
+C
4
sinh(
β
z)cos(
β
z) . (7.12)
Notice that (7.11) and (7.12) are equivalent because of the identities
cosh(
β
z) =
e
β
z
+ e
−
β
z
2
; sinh(
β
z) =
e
β
z
−e
−
β
z
2
.
In fact, (7.12) can be obtained from (7.11) by writing
B
1
=
C
1
−C
4
2
; B
2
=
C
2
+C
3
2
; B
3
=
C
1
+C
4
2
; B
4
=
C
3
−C
2
2
.
The reader uncomfortable with the complex algebra leading to equations (7.11, 7.12)
is encouraged to verify them by direct substitution into (7.6).
7.2.1 The semi-infinite beam
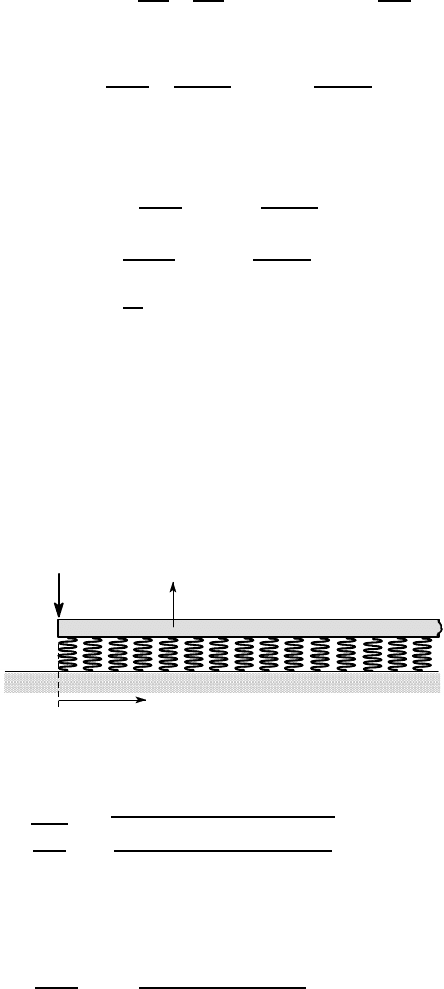
Figure 7.4 shows a semi-infinite beam, z> 0, loaded by a force F
0
and a moment M
0
at the end z = 0. The displacement must be bounded as z →∞ and hence only the
exponentially decaying terms should be retained from (7.11), giving
u(z) = B
3
e
−
β
z
cos(
β
z) + B
4
e
−
β
z
sin(
β
z) . (7.13)
u(z)
z
F
0
0
M
Figure 7.4: The semi-infinite beam loaded only at the end

358 7 Beams on Elastic Foundations
A more rigorous argument showing that the exponentially growing terms should be
dropped can be obtained by considering a beam of finite length L, where
β
L ≫1.
In this case, all four terms in (7.11) should be retained in order to satisfy the two
boundary conditions at each end, but it will be found that the coefficients B
1
,B
2
→0
as
β
L →∞, for any boundary conditions on the end z = L. We shall consider finite
beam problems further in §7.6 below.
Progressive derivatives of equation (7.13) with respect to z provide corresponding
expressions for the slope
θ
, bending moment M, and shear force V as functions of z.
We have
θ
≡
du
dz
= −B
3
β
e
−
β
z
[cos(
β
z) + sin(
β
z)]
+B
4
β
e
−
β
z
[cos(
β
z) −sin(
β
z)] (7.14)
M = −EI
d
2
u
dz
2
= −2B
3
EI
β
2
e
−
β
z
sin(
β
z)
+2B
4
EI
β
2
e
−
β
z
cos(
β
z) (7.15)
V =
dM
dz
= −2B
3
EI
β
3
e
−
β
z
[cos(
β
z) −sin(
β
z)]
−2B
4
EI
β
3
e
−
β
z
[cos(
β
z) + sin(
β
z)] . (7.16)
It is convenient to define the four functions
f
1
(x) = e
−x
cosx ; f
2
(x) = e
−x
sinx ; f
3
(x) = e
−x
(cosx + sinx) ;
f
4
(x) = e
−x
(cosx −sinx) , (7.17)
which permit equations (7.13–7.16) to be written in the compact form
u(z) = B
3
f
1
(
β
z) + B
4
f
2
(
β
z) (7.18)
θ
(z) = −B
3
β
f
3
(
β
z) + B
4
β
f
4
(
β
z) (7.19)
M(z) = −
B
3
k
2
β
2
f
2
(
β
z) +
B
4
k
2
β
2
f
1
(
β
z) (7.20)
V (z) = −
B
3
k
2
β
f
4
(
β
z) −
B
4
k
2
β
f
3
(
β
z) , (7.21)
where we have used (7.9) to eliminate the flexural rigidity EI in favour of the mod-
ulus k in equations (7.20, 7.21). It can be verified by substitution that the functions
f
1
, f
2
, f
3
, f
4
satisfy the relations
f
1
=
1
2
( f
3
+ f
4
) ; f
2
=
1
2
( f
3
− f
4
) ; f
3
= f
1
+ f
2
; f
4
= f
1
− f
2
(7.22)
and
d f
1
dx
= −f
3
;
d f
2
dx
= f
4
;
d f
3
dx
= −2 f
2
;
d f
4
dx
= −2 f
1
. (7.23)
Equations (7.18–7.21) can be used to determine the constants B
3
,B
4
for any two
boundary conditions at the end z=0. For the case illustrated in Figure 7.4, we have
7.2 The homogeneous solution 359
F
0
= V (0) = −
B
3
k
2
β
−
B
4
k
2
β
; M
0
= M(0) =
B
4
k
2
β
2
and hence
B
3
= −
2
β
F
0
k
−
2
β
2
M
0
k
; B
4
=
2
β
2
M
0
k
.
Substituting into (7.18–7.21) and using (7.22) to simplify the resulting expres-
sions, we obtain
u(z) = −
2
β
F
0
k
f
1
(
β
z) −
2
β
2
M
0
k
f
4
(
β
z) (7.24)
θ
(z) =
2
β
2
F
0
k
f
3
(
β
z) +
4
β
3
M
0
k
f
1
(
β
z) (7.25)
M(z) =
F
0
β
f
2
(
β
z) + M
0
f
3
(
β
z) (7.26)
V (z) = F
0
f
4
(
β
z) −2M
0
β
f
2
(
β
z) . (7.27)
Example 7. 1
A semi-infinite steel beam of second moment of area I
x
=0.5 ×10
6
mm
4
is supported
on an elastic foundation of modulus k = 10 MPa and loaded by a downward force
F
0
=10 kN at the end, as shown in Figure 7.5. Find the slope and deflection at the free
end and the location and magnitude of the maximum bending moment (E
steel
= 210
GPa).
Figure 7.5: The semi-infinite beam loaded by an end force
We first use equation (7.9) to calculate
β
=
4
r
k
4EI
=
4
s
10 ×10
6
4 ×210 ×10
9
×0.5 ×10
−6
= 2.209 m
−1
.
The complete solution can be obtained by substituting F
0
= 10 kN, M
0
= 0 into
equations (7.24–7.27). In particular, the end displacement and slope are
u(0) = −
2
β
F
0
k
= −
2 ×2.209 ×10 ×10
3
10 ×10
6
= −4.4 ×10
−3
m
— i.e. 4.4 mm downwards, and
u(z)
z
F
0
360 7 Beams on Elastic Foundations
θ
(0) =
2
β
2
F
0
k
=
2 ×2.209
2
×10 ×10
3
10 ×10
6
= 9.8 ×10
−3
radians (0.56
o
) .
To find the maximum bending moment, we first note that
dM
dz
= V = −
−
2
β
F
0
k
k
2
β
f
4
(
β
z) = F
0
e
−
β
z
[cos(
β
z) −sin(
β
z)] ,
using (7.24). The maximum bending moment occurs when dM/dz= 0 and hence
cos(
β
z) −sin(
β
z) = 0 .
This equation has roots at
β
z =
π
4
,
5
π
4
,
9
π
4
,...
In view of the exponential decay, the magnitude of M will be greatest at the first root,
where
z =
π
4
β
=
π
4 ×2.209
= 0.356 m .
At this point, we have
M
max
=
F
0
e
−
π
/4
√
2
β
= 0.322
F
0
β
=
0.322 ×10 ×10
3
2.209
= 1457 Nm .
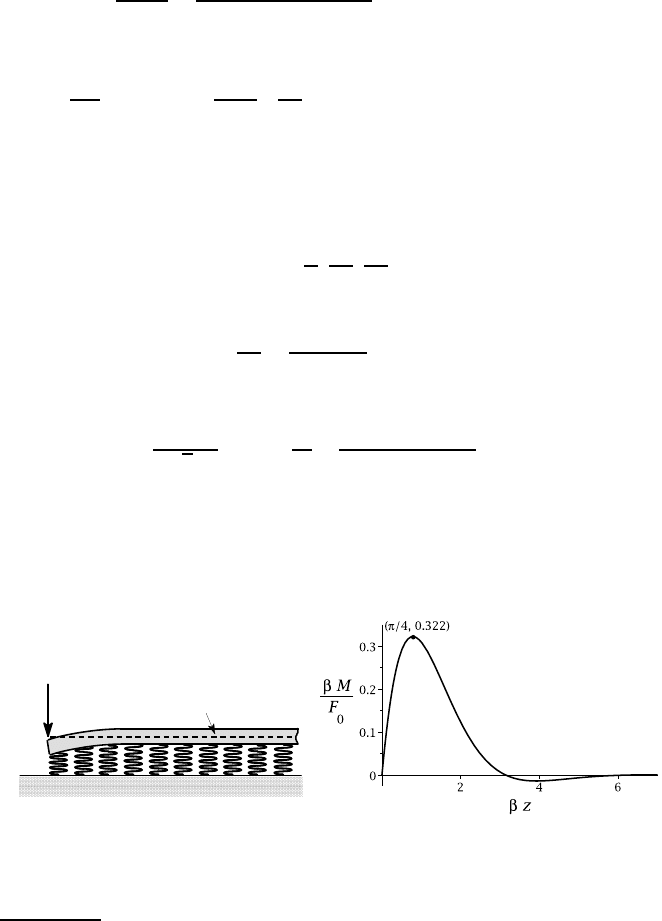
Figure 7.6 shows the deformed shape of the beam and the bending moment as a
function of z. Notice that the disturbance decays rapidly with z, but the trigonometric
functions in equations (7.13–7.16) cause the decay to be oscillatory, so there are
actually regions in which the beam is displaced upwards
3
by the downward force F
0
.
(b)
Figure 7.6: (a) Deformed shape of the beam and (b) the bending moment distribution
3
If the beam is simply resting on the support, rather than being attached to it, an upward
displacement will cause the beam to separate from the foundation and the restoring force
p(z) will then be locally zero, rather than being given by equation (7.1). A foundation of
this kind that exerts a restoring force only for displacements in one direction is known as a
unilateral support. However, in problems with downward loading, the weight of the beam
will probably be sufficient to maintain contact in the upward displacement regions.
F
0
original centreline
(a)
7.3 Localized nature of the solution 361
7.3 Locali zed nature of the solution
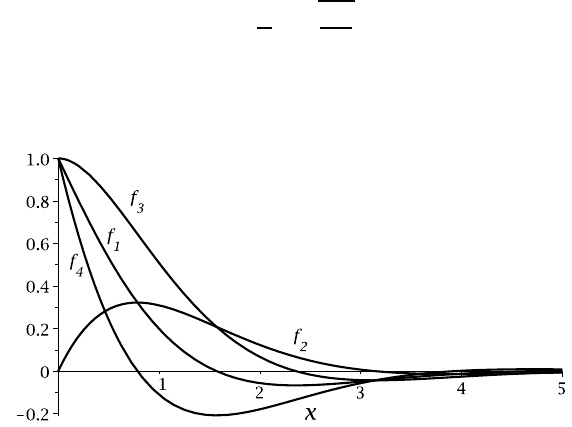
The rapid decay of the disturbance observed in the above example is typical of end
loading problems for beams on elastic foundations. Figure 7.7 shows the four func-
tions f
1
, f
2
, f
3
, f
4
, of equations (7.17) and all have esentially decayed to negligible
values at x= 4. In view of equations (7.18–7.21), we conclude that for any end load-
ing of the beam, the deformation will be restricted to a region at the end defined
approximately by
0 < z < 4l
0
, (7.28)
where
l
0
≡
1
β
=
4
r
4EI
k
(7.29)
has the dimensions of length and functions as a characteristic decay length for the
beam/support system. For Example 7.1, the decay length was l
0
= 1/2.209 = 0.453
m.
Figure 7.7: The functions f
1
, f
2
, f
3
, f
4
, of equations (7.17)
In any practical problem involving a beam on an elastic foundation, the very
first step should always be to calculate l
0
from the properties of the beam and the
foundation. Comparison of this length with other length scales in the problem then
provides important information about the behaviour of the system and can often be
used to justify a simpler solution procedure. If the length of the beam L ≫l
0
(i.e. if
β
L ≫1), it follows that end loads on the beam will have only local effects and there
will be a central region, distant from the ends, where the beam will be unaffected
by the end conditions. This condition is often satisfied in practice and it simplifies
the resulting problem, since effects at the two ends can then be analyzed separately,
using equations (7.18–7.21).
Similar localization occurs when loads are applied over a restricted central region
of the beam. If the loads are at least 4l
0
from either end of the beam, their effects will
not be influenced by conditions at the ends and it is sufficient to solve the simpler
problem in which the same loads are applied to an infinite beam (see §7.4 below).
362 7 Beams on Elastic Foundations
non-local displacements
Figure 7.8: Estimation of the significance of non-local effects
We can also use an estimate of l
0
to determine whether a more realistic ‘non-
local’ foundation can be approximated by an equivalent Winkler foundation in a
particular application (see Figure 7.1 and the associated discussion). Suppose a uni-
form load is applied to the non-local foundation over an extended region, as shown
in Figure 7.8. The Winkler approximation is reasonable if the regions of significant
non-local displacements adjacent to the load extend a distance significantly smaller
than l
0
.
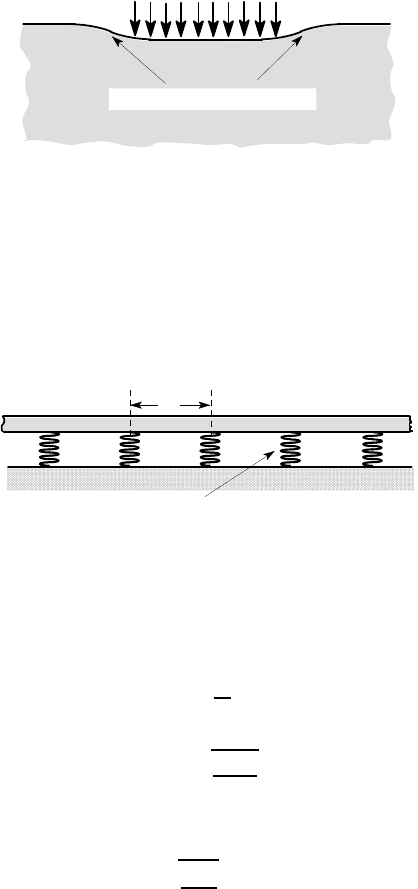
Figure 7.9: A beam supported on discrete springs with spacing d
Another case of some interest concerns a beam supported on a set of discrete
springs, as shown in Figure 7.9. If the springs each have stiffness k
s
and the distance
between adjacent springs is d, the effective modulus of the foundation (the stiffness
associated with a unit length) will be
k =
k
s
d
, (7.30)
giving
l
0
=
4
r
4EId
k
s
. (7.31)
We can then argue that representation of the discrete springs as a continuous founda-
tion will be reasonable if d ≪ l
0
and hence
4
r
d
3
k
s
4EI
≪ 1. (7.32)
7.4 Concentrated force on an infinite beam
In view of the preceding discussion, it is of interest to consider the problem of Fig-
ure 7.10 (a), in which an infinite beam on an elastic foundation is loaded by a con-
centrated force F
0
. We can locate the origin at the point of application of the force
without loss of generality.
d
stiffness k
s
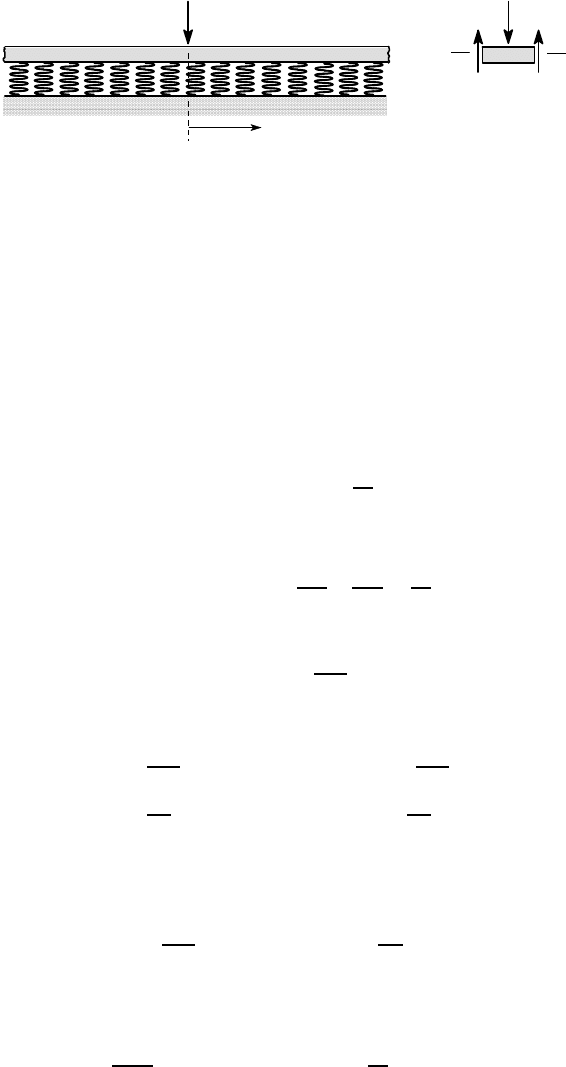
7.4 Concentrated force on an infinite beam 363
F
0
F
0
2
F
0
2
(a) (b)
Figure 7.10: (a) Infinite beam loaded by a concentrated force, (b) equilibrium of an
infinitesimal element at O
Strictly speaking, this is an inhomogeneous problem in which the load w(z) =
F
0
δ
(z), where
δ
(z) is the Dirac delta function. However, we can reduce the prob-
lem to a homogeneous problem for the semi-infinite beam z > 0 using a symmetry
argument.
The problem is symmetrical about O and hence the slope
θ
must be zero at O.
Furthermore, equilibrium of an infinitesimal beam element immediately under the
load [Figure 7.10 (b)] shows that the shear force immediately to the right of the force
must be F
0
/2. Thus the region z> 0 has end conditions
θ
(0) = 0 ; V (0) =
F
0
2
.
Substituting into equations (7.19, 7.21), we obtain the two simultaneous equations
−B
3
+ B
4
= 0 ; −
B
3
k
2
β
−
B
4
k
2
β
=
F
0
2
for B
3
,B
4
, with solution
B
3
= B
4
= −
F
0
β
2k
.
It follows from (7.18, 7.20) that
u(z) = −
F
0
β
2k
e
−
β
z
[cos(
β
z) + sin(
β
z)] = −
F
0
β
2k
f
3
(
β
z) (7.33)
M(z) = −
F
0
4
β
e
−
β
z
[cos(
β
z) −sin(
β
z)] = −
F
0
4
β
f
4
(
β
z) (7.34)
in z>0. The symmetry of the problem requires that the same solution can be used in
z< 0 with z replaced by −z. Thus, expressions that are correct for all values of z can
be written
u(z) = −
F
0
β
2k
f
3
(
β
|z|) ; M(z) = −
F
0
4
β
f
4
(
β
|z|) . (7.35)
The slope
θ
and shear force V are odd functions of z (e.g. V(z) = −V (−z)) and can
be written
θ
(z) =
F
0
β
2
k
sgn(z) f
2
(
β
|z|) ; V (z) =
F
0
2
sgn(z) f
1
(
β
|z|) , (7.36)
z
O
F
0

364 7 Beams on Elastic Foundations
using (7.3, 7.21), where sgn(z)=1 for z>0 and −1 for z< 0.
The maximum displacement and bending moment occur under the load at z = 0
and are
u
max
= u(0) = −
F
0
β
2k
; M
max
= M(0) = −
F
0
4
β
. (7.37)
The deformed shape of the beam is shown in Figure 7.11. As in Example 7.1 [Figure
7.6 (a)], the decay of the disturbance is oscillatory, so there are regions where the
downward force causes an upward (albeit small) displacement.
Figure 7.11: Deformation of the beam under a concentrated force
7.4.1 More general loading of the infinite beam
The preceding solution can be extended to problems involving several concentrated
forces, using superposition. For example, if forces F
1
,F
2
,F
3
act at the points z =
a
1
,a
2
,a
3
respectively, as shown in Figure 7.12, the resulting displacement will be
u(z) = −
F
1
β
2k
f
3
(
β
|z −a
1
|) −
F
2
β
2k
f
3
(
β
|z −a
2
|) −
F
1
β
2k
f
3
(
β
|z −a
3
|) ,
from (7.35). A similar expression can be written for the moment M(z).
Figure 7.12: Infinite beam with several concentrated forces
The same method can be extended to the case of a distributed load w(z) in a <
z <b by considering it to consist of a set of concentrated forces
4
w(z
′
)
δ
z
′
, as shown
in Figure 7.13.
4
Notice that this is another case where we need to introduce a second variable z
′
for the
purposes of integration (cf §6.1.4).
O
z
F
0
O
z
a
1
a
2
a
3
F
3
F
1
F
2
