Barber J.R. Intermediate Mechanics of Materials
Подождите немного. Документ загружается.


Problems 345
6.23. The unsymmetrical square box section of Figure P6.23 transmits a vertical
shear force V
y
whose line of action passes through the middle of the thicker left-hand
section as shown. Find the maximum shear stress in the section.
a
a
t
t
t
2t
V
y
Figure P6.23
6.24. The closed thin-walled section of Figure P6.24 transmits a vertical shear force
V
y
, whose line of action passes through the point O. Find the distribution of shear
stress in the section.
V
y
30
o
30
o
t
O
a
Figure P6.24

346 6 Shear and Torsion of Thin-walled Beams
Section 6.5
6.25. The symmetric box section of Figure P6.25 is loaded by a torque of 4 kNm.
Find the location and magnitude of the maximum shear stress and the twist per unit
length if G=80 GPa.
10
80
120
20
10
all dimensions in mm
Figure P6.25
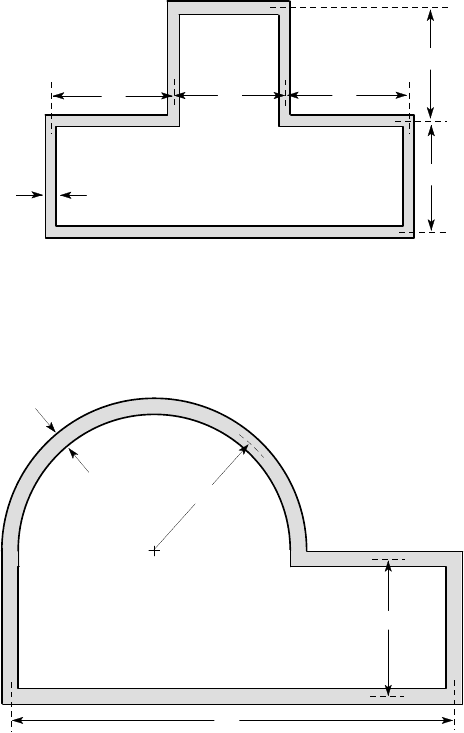
6.26. The hollow thin-walled box section of Figure P6.26 has sides a,b and wall
thickness t and is subjected to a torque T . Find the shear stress distribution and
the torsional stiffness K. Express the results in terms of the perimeter of the section
p=2(a +b) and the ratio r=a/b between the sides. Hence show that a square section
(r =1) has the greatest stiffness and strength for a given volume of material.
a
t
t
b
T
Figure P6.26
Problems 347
6.27. A beam with the section of Figure P6.24 is loaded by a torque T . Find the
maximum shear stress and the twist per unit length, if the material has shear modulus
G.
6.28. Find the torsional stiffness K for the closed thin-walled beam section of Figure
P6.28. The wall thickness is everywhere equal to t.
t
a
a
a
a
a
Figure P6.28
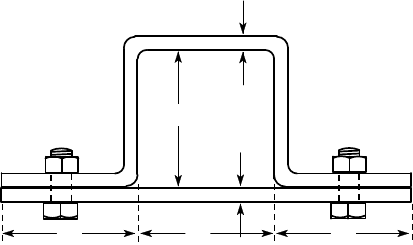
6.29. Find the torsional stiffness K for the closed thin-walled beam section of Figure
P6.29. The wall thickness is everywhere equal to t.
a
t
3a
a
Figure P6.29
6.30. A beam with the section of Figure P6.20 is loaded by a torque T . Find the
maximum shear stress and the twist per unit length, if the material has shear modulus
G.
348 6 Shear and Torsion of Thin-walled Beams
6.31. A beam with the section of Figure P6.21 is loaded by a torque T . Find the
maximum shear stress and the twist per unit length, if the material has shear modulus
G.
6.32. The torsional stiffness of a hat section is to be increased by bolting a flat plate
to it, creating the closed section of Figure P6.32. The bolts are of 3 mm diameter and
have an axial spacing of 50 mm. Estimate the shear stress in the bolts when the beam
is loaded by a torque of 10 Nm.
2
2
20
20
20
20
all dimensions in mm
Figure P6.32
Section 6.6
6.33. Find the twist per unit length for Problem 6.19, if the material has shear mod-
ulus G.
6.34. Find the twist per unit length for Problem 6.20, if the material has shear mod-
ulus G.
6.35. Find the twist per unit length for Problem 6.21, if the material has shear mod-
ulus G.
6.36. Find the twist per unit length for Problem 6.24, if the material has shear mod-
ulus G.
6.37. Find the location of the shear centre for the triangular section of Figure P6.19.
6.38. Find the location of the shear centre for the section of Figure P6.20.

Problems 349
6.39. Find the location of the shear centre for the unsymmetrical box section of Fig-
ure P6.23.
6.40. Find the location of the shear centre for the section of Figure P6.24.
6.41. Find the location of the shear centre for the closed thin-walled section of Figure
P6.41.
t
O
2t
a
Figure P6.41
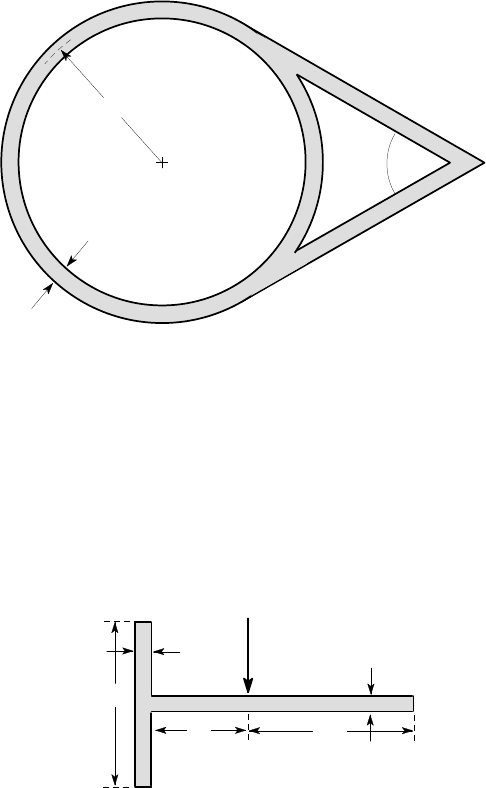
6.42. The two-cell, thin-walled beam section of Figure P6.42 is loaded by a torque
T . Find the location and magnitude of the maximum shear stress and the torsional
stiffness K for the section. The wall thickness is everywhere equal to t. Compare your
results with those obtained when there is no internal partition, as in Figure P6.28.
t
a
a
a
a
a
Figure P6.42
350 6 Shear and Torsion of Thin-walled Beams
6.43. The two-cell, thin-walled beam section of Figure P6.43 is loaded by a torque
T . Find the location and magnitude of the maximum shear stress and the torsional
stiffness K for the section. The wall thickness is everywhere equal to t.
t
O
a
o
60
Figure P6.43
Section 6.7
6.44. Find the torsional stiffness K for the cresent section of Figure P6.6.
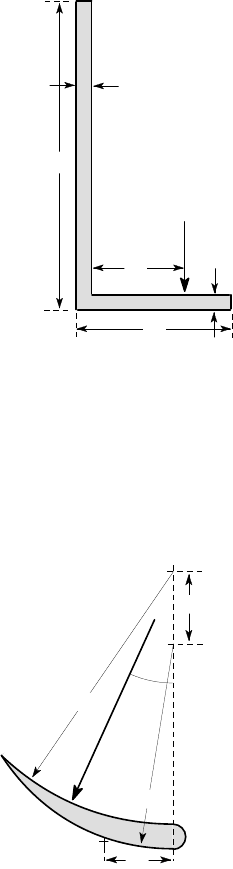
6.45. The T-beam of Figure P6.45 transmits a shear force of 20 kN with the line of
action shown. Find the maximum shear stress and the twist per unit length, if the
material is steel with G=80 GPa.
20 kN
10
10
100
100
70
all dimensions in mm
Figure P6.45
6.46. The unequal angle of Figure P6.46 is loaded by a shear force of 6 kN with the
line of action shown. Find the twist per unit length, if the material of the beam is
steel with G= 80 GPa.
Problems 351
6 kN
4
4
40
80
24
all dimensions in mm
Figure P6.46
6.47*. Use the results of §6.6 to find the twist per unit length for Problem 6.22. Use
your result to determine the line of action of V
y
for which the open section of Figure
P6.5 h as no twist. Com ment on the implication o f your result for the statement that
the shear centre is that point through which V
y
must act in order that there be no twist.
500 N
24
o
12
35
43
12
C
.
P
all dimensions in mm
Figure P6.48
6.48*. A titanium alloy turbine blade is idealized by the section of Figure P6.4 8.
The leading edge is a semicircle of radius 2 mm an d the inner an d outer edges of
the trailing section are cylindrical surfaces o f radius 43 mm and 35 mm respectively,
with centres as shown. The shear centre is located at C and the blade is loaded by
352 6 Shear and Torsion of Thin-walled Beams
a 500 N force no rmal to the inner surface at P as shown. Find the maximum shear
stress due to torsion and the twist of the blade per unit length . The shear modulus for
the alloy is 43 GPa.
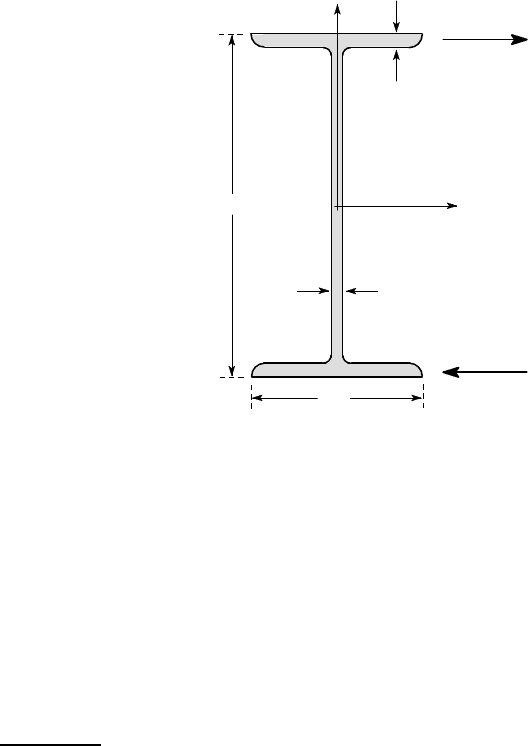
6.49. The W200×22 I-beam of Figure P6.49 is made of steel (G = 80 GPa) and is
15 m long . One end is built in and the other is loaded by two forces F constituting
a torque, as shown. Find the torsional stiffness K for the beam section and hence
determine the value of F needed to cause the end to twist through an angle of 20
o
.
Does the result surprise you? How large an angle of twist
12
could a person of average
strength produ ce in such a beam using his or her hands only?
102
6.2
8
206
O x
y
F
F
all dimensions in mm
Figure P6.49
6.50. The beam of Figure P6.1 is loaded by a torque of 40 Nm. Find the m aximum
shear stress and the twist per unit length, if the material is steel with G = 80 GPa.
6.51. The shear force in Problem 6.2 is displaced b y 1 inch from the plane of symme-
try. Find the percentage increase in the maximum shear stress caused by this offset.
6.52. Use the results of §6.7 to answer Problem 1.19 for the angle iron and compare
the results with experiment.
12
If you want to impress your unsuspecting colleagues with your engineering expertise (or
your immense strength), ask them to guess the answer to this question, along the li nes of
the questions in §1.2, and then perform the experiment.

7
Beams on Elastic Foundations
Many engineering applications involve a relatively rigid structure supported by a
more flexible distributed ‘foundation’. An important class of examples arises in civil
engineering, where buildings or other structures are supported on a soil base. Other
less obvious examples include steel components supported on extended rubber bush-
ings, floating structures (where the support is provided by the buoyancy force) and
the transmission of load between bones through an intervening cartilidge or other
softer tissue layer. The roughness and/or lack of conformity between contacting bod-
ies can also simulate an intervening softer foundation. In all these cases, the founda-
tion has the effect of distributing the load over a more extended area. For example,
the weight of a locomotive transmitted to the track through the relatively concen-
trated wheel/rail contact will be distributed over quite an extended region as a result
of the compliance of the ballast and soil foundation. An important objective in ana-
lyzing such problems is to determine the extent of this distribution in order to choose
appropriate properties for the foundation materials.
A linear elastic foundation is any form of distributed support in which the dis-
placement is a linear function of the applied load. In general, if we apply a localized
load to a foundation, the maximum displacement will occur under the load, but ad-
jacent regions of the surface will also be displaced, as shown in Figure 7.1. You can
demonstrate this effect by pressing the sharp edge of a ruler into a rubber eraser
resting on a plane surface. The extent of this non-local displacement depends on the
geometry of the foundation and also its material properties. Displacements tend to
be more localized if the elastic modulus of the foundation material increases with
depth
1
as in the case of many soils, or if the foundation comprises a thin layer of
flexible material resting on or bonded to a rigid base.
2
1
C.R. Calladine and J.A. Greenwood (1978), Line and point loads on a non-homogeneous
incompressible elastic half-space, Quarterly Journal of Mechanics and Applied Mathemat-
ics, Vol.31, pp.507–529.
2
K.L. Johnson (1985), Contact Mechanics, Cambridge University Press, Cambridge, §5.8.
J.R. Barber, Intermediate Mechanics of Materials, Solid Mechanics and Its Applications 175,
2nd ed., DOI 10.1007/978-94-007-0295-0_7, © Springer Science+Business Media B.V. 2011

354 7 Beams on Elastic Foundations
Figure 7.1: Surface displacements due to a localized load
A limiting case is the Winkler foundation, in which the displacement u(z) at a
point defined by the coordinate z depends only upon the local force per unit length
p(z) — i.e.
u(z) =
p(z)
k
, (7.1)
where k is known as the modulus or the stiffness of the foundation. The modulus is
the support per unit length of beam, per unit displacement, and it therefore has the
same dimensions as a stress (force/length
2
). The Winkler foundation acts essentially
like a bed of unconnected springs, as shown in Figure 7.2. Equation (7.1) leads to
significant simplification in the analysis of problems and hence is often used as an
approximation in situations where the foundation displacement is not strictly local.
We shall discuss ways of determining whether this is an appropriate simplification in
§7.3 below.
Figure 7.2: Schematic representation of the Winkler foundation
7.1 The governing equation
Figure 7.3 (a) shows a uniform beam of flexural rigidity EI, supported by a Winkler
foundation and subjected to a distributed load w(z) per unit length. The forces acting
on a small element of beam of length
δ
z are shown in Figure 7.3 (b). The force
corresponding to the distributed load is w(z)
δ
z and the support provides a downward
force p(z)
δ
z opposing the upward displacement u(z).
Elastic body
Rigid base
