Barber J.R. Intermediate Mechanics of Materials

Подождите немного. Документ загружается.

10.5 Plastic deformation of disks and cylinders 475

The elastic zone

In the elastic zone c <r <a, the stresses are given by equations (10.21, 10.22) as

= −

(3 +

)

ρΩ

+ A +

θθ

= −

(1 + 3

)

ρΩ

+ A −

In contrast to the ﬁrst yield solution, the constant B is not here required to be zero,

since the centre r =0 is not included in the elastic range c<r < a.

The two constants A,B and the unknown radius c are determined from the

traction-free condition

(a) = 0 at the outer radius and the two continuity condi-

tions

−

θθ

−

) at r =c. Substituting for the appropriate

stresses, we obtain

−

(3 +

)

ρΩ

+ A +

= 0

−

(3 +

)

ρΩ

+ A +

= S

−

ρΩ

−

(1 + 3

)

ρΩ

+ A −

= S

Eliminating A,B between these equations, we obtain





−2





(1 + 3

)



(3 +

) −

ρΩ



= 0 ,

which has the solution





= 1 −

(1 + 3

)



Ω

−1



, (10.39)

where we have taken the negative square root, since physically meaningful results

require that 0<c< a.

Complete plastic failure corresponds to the case c=a (i.e. the plastic zone extends

over the whole disk) and hence

Ω

The ratio

Ω

3(3 +

)

increases with

, but is less than 1.15 even at the maximum possible value of

=0.5.

Thus, the speed at complete plastic failure is never more than 15% higher than that at

476 10 Thick-walled Cylinders and Disks

ﬁrst yield. From a design perspective, most of the interesting results can be obtained

from the elastic ‘ﬁrst yield’ analysis and the fully plastic analysis. In the present case,

the latter can of course be obtained directly by imposing the edge condition

= 0

at r = a in the expression for the stresses in the plastic zone.

For this reason, the complexities of an elastic-plastic solution are not justiﬁed in

most practical applications. One exception is Problem 10.21, which describes a test

method for determining the properties of soils.

10.5.4 Other failure modes

There is no guarantee that failure of the cylinder or disk will involve plastic defor-

mation at all radii. For example, an annular disk with a large ratio between inner and

outer radii (such as Problem 10.22) and loaded by internal pressure will fail as soon

as the internal pressure reaches the yield stress in compression and before yielding

has progressed to the outer radius. The innermost layer of material will then yield

in compression, since there is no restraint to axial motion (

=0), and we shall see

a thin layer of material extruded in the axial direction, much as a layer of viscous

liquid could be squozen out from the interface between two disks during a shrink ﬁt.

Problems exhibiting this kind of behavior can generally be identiﬁed by the fact

that the attempt to solve the fully-plastic problem runs into difﬁculties. For example,

the fully-plastic solution for the thick-walled cylinder in §10.5.2 above breaks down

if it predicts

θθ

at the inner radius. This is again an indication that we might

expect axial extrusion of material at the inner radius. However, the cylinder differs

from the disk in that there is nowhere for the material to go. In fact, the assumption

that plane sections remain plane demands that stresses resisting this axial motion

will be developed. As a result, the axial stress distribution

will deviate from

equation (10.31) (which was developed from elastic arguments) sufﬁciently to ensure

that axial motion of material does not occur. In effect,

will decrease at the inner

radius, sufﬁciently to leave (

θθ

−

) as the greatest stress difference, and increase

at the outer radius in order to preserve axial equilibrium. This process can continue

until the whole cylinder is plastic.

10.5.5 Unloading and residual stresses

If a cylinder or disk is loaded into the plastic range and then unloaded, the unloading

process will generally move the stress state inside the yield envelope and hence be

elastic. In extreme cases, complete unloading might cause the state to reach the yield

envelope at a different point and hence cause additional plastic deformation, but

this possibility can be detected by performing an elastic analysis and checking the

predicted ﬁnal stress state.

If unloading is complete (i.e. if the ﬁnal tractions, rotational speed and tempera-

tures are returned to zero), the ﬁnal residual stress ﬁeld is obtained from that at the

maximum load by subtracting the ﬁeld that would have been obtained at the max-

imum load had the system remained elastic. The reader will recall that a similar

10.5 Plastic deformation of disks and cylinders 477

procedure was used in §5.7 to determine the residual stress distribution in a beam

loaded into the plastic range and then released.

The more general case where the loading is reduced, but not necessarily to zero,

can be treated by ﬁnding the residual stress and then superposing the elastic stresses

associated with the ﬁnal loading. Alternatively, we can start from the stress ﬁeld

at the maximum load and superpose an elastic ﬁeld corresponding to the difference

between the maximum and the ﬁnal load. Notice however that the elastic ﬁeld varies

with the square of the rotational speed, so if the speed changes from

Ω

, the

corresponding terms in this differential ﬁeld will contain

Ω

−

Ω

Example 10.5 — The rotating disk

A solid disk of radius a starts from rest, accelerates up to the fully-plastic rotational

speed

Ω

and then returns to rest. Determine the residual stress ﬁeld in the disk, if

the material has Young’s modulus E, Poisson’s ratio

and tensile yield stress S

The analysis of this problem during the loading phase has already been per-

formed in Example 10.4 above. In particular, the elastic solution is

(3 +

)

ρΩ

−r

)

;

θθ

ρΩ



(3 +

−(1 + 3



and the fully plastic solution is

= S

−

ρΩ

;

θθ

= S

with

Ω

To ﬁnd the residual stresses we must subtract, from the fully-plastic solution,

the stresses that would be produced at a rotational speed of

Ω

if the material had

remained elastic — i.e. if there had been no plastic deformation. This in turn is

obtained by substituting

Ω

in the elastic equations above. Thus, the residual

stresses are

= S

−

ρΩ

−

(3 +

)

ρΩ

−r

)

θθ

= S

−

ρΩ



(3 +

−(1 + 3



After substituting for

Ω

, these expressions simplify to

= −

(1 + 3

)



1 −



;

θθ

(1 + 3

)



−1



The stresses (including

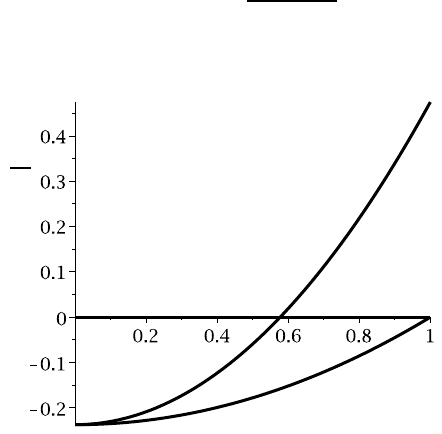
= 0) are illustrated in Figure 10.16. Notice that the

maximum stress difference occurs at the outer edge (r =a) and is

478 10 Thick-walled Cylinders and Disks

θθ

(a) −

(a) =

(1 + 3

)

Since this value is less than S

, we conclude that there will be no further yielding

during unloading.

θθ

r/a

Figure 10.16: Residual stresses in the disk after rotation to near

Ω

(

=0.3)

10.6 Summary

In this chapter, we have developed methods for determining the stresses in cylinders

and disks under axisymmetric loading. Applications include thick-walled pressure

vessels, rotating wheels and disks, and stresses associated with shrink and press ﬁts.

The stresses must satisfy Newton’s second law, the strains must satisfy a kine-

matic compatibility relation and the stresses and strains are related through the con-

stitutive behavior of the material. These factors can be combined to deﬁne the gov-

erning ordinary differential equation for a material with any constitutive law. Radial

traction or displacement can be prescribed at the inner and outer radii. The method

was illustrated here for elastic and elastic-plastic materials, including the effects of

rotation and thermal expansion.

The internal pressure required to cause yielding throughout a thick walled pres-

sure vessel is signiﬁcantly larger than that for ﬁrst yield and a single overload con-

dition leaves a state of residual stress that will prevent plastic deformation under

more moderate loading. Similar favourable residual stress states can be developed

by shrinking one thick cylinder onto another.

Further reading

W.B. Bickford (1998), Advanced Mechanics of Materials, Addison Wesley, Menlo

Park, CA, Chapter 6.

Problems 479

A.P. Boresi, R.J. Schmidt, and O.M. Sidebottom (1993), Advanced Mechanics of

Materials, John Wiley, New York, 5th edn., Chapter 11.

A.H. Burr (1981), Mechanical Analysis and Design, Elsevier, New York, §§8.6–8.14.

Problems

Sections 10.1—10.3

10.1. A rotating disk of radius b has a small central hole of radius a (≪b). If all the

surfaces of the disk are traction-free, show that the hole causes a stress concentration

of 2 — i.e. that the maximum tensile stress is twice as large as that in a similar disk

without a hole, rotating at the same speed.

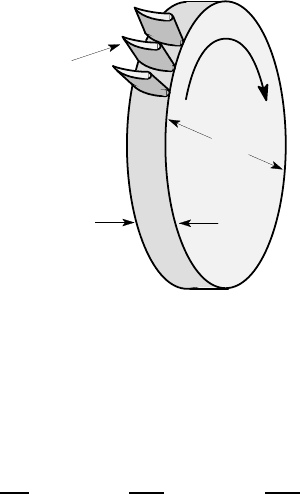
10.2. The turbine disk of Figure P10.2 comprises a solid central disk of diameter 800

mm and thickness 50 mm, to which are attached 50 blades, each of mass 0.4 kg. The

centres of mass of the blades lie on a circle of radius 430 mm. Find the maximum

tensile stress in the disk when the rotational speed is 10,000 rpm. The disk is made

of steel for which E =210 GPa,

=0.3 and

=7700 kg/m

10,000 rpm

800

blades

all dimensions in mm

Figure P10.2

10.3. During a test on an automotive disk brake, it was found that the temperature T

of the disk could be approximated by the expression

T =

(1 −e

−

) −

(1 −e

−

) +

−

where

= t/t

is a dimensionless time, a is the radius of the disk, r is the distance

from the axis, t is time and T

are constants. The disk is continuous at r=0 and all

its surfaces can be assumed to be traction-free.

480 10 Thick-walled Cylinders and Disks

Derive expressions for the radial and circumferential thermal stresses as func-

tions of radius and time, and hence show that the maximum value of the stress dif-

ference (

θθ

−

) at any given time always occurs at the outer edge of the disk.

10.4. A long hollow cylinder has outside diameter 25 inches and inside diameter 15

inches. It is made of steel (E = 30×10

psi,

= 0.3) and is loaded by an external

pressure of 600 psi. The ends of the vessel are prevented from moving axially. Find

the maximum compressive stress in the cylinder and the change in diameter of the

central hole.

10.5. The fuel rods of a nuclear reactor consist of solid uranium cylinders of diam-

eter 70 mm. During operation, a typical rod experiences a temperature distribution

approximated by the equation

T (r) = 600 −0.1r

2 o

C ,

where r is in mm. Find the maximum stress in the fuel rod if the outer surface is

traction-free and plane strain conditions can be assumed. The properties of uranium

are E =172 GPa,

=0.28,

=11×10

−6

per

10.6. A concrete drainpipe has inside diameter 30 inches and wall thickness 4 inches.

When dry, it is loaded by external soil pressure of 10 psi and when full, the maximum

internal pressure is 30 psi. Determine the factor of safety against failure if concrete

obeys the modiﬁed Mohr criterion (§2.2.4) with S

= 0.6 ksi, S

= 5.0 ksi. Assume

that the axial stress

=0.

10.7. A cylinder of internal radius a and external radius b is loaded by internal pres-

sure p. Find an expression for the maximum tensile stress. Then use the membrane

theory of Chapter 8 to obtain an approximate solution of the same problem, treating

the radius of the shell as the mean radius (a+b)/2. What is the maximum value of

the ratio b/a for which the membrane solution is in error by less than 10%?

10.8. A thick elastic cylinder of inside radius a and outside radius 2a is loaded by

internal pressure p. At the outer radius, radial displacement u

is prevented by a

rigid reinforcing sleeve. Also, the cylinder is prevented from expanding in the axial

direction (e

=0).

Find the three stress components

θθ

and sketch a graph of the resulting

functions of radius. Where, and at what internal pressure, will yield ﬁrst occur if the

material has a yield stress S

in uniaxial tension and obeys Tresca’s yield criterion?

Comment on the results for the case where Poisson’s ratio

=0.5.

10.9*. A cylinder is fabricated from a composite material with the ﬁbres laid down

in the circumferential direction, such that the constitutive law is

θθ

Problems 481

where E

= 4E

. (Note that Poisson’s ratio is zero). Use these expressions and the

equilibrium and compatibility conditions to ﬁnd the differential equation satisﬁed

by the radial stress

for the case where there is no rotation and no temperature

variation. Solve this equation using the identity

−i−j









≡

(2i + j)

d f

i(i + j −1) f

(You will need to ﬁnd the appropriate values of i, j to make the right hand side corre-

spond to your differential equation and then use the equivalent left hand side form.)

Use your solution to ﬁnd the stresses in a cylinder of inside radius a and outside

radius 2a, subjected to an internal pressure p.

10.10*. Use the plane stress constitutive relations (10.14, 10.15) to eliminate the

strains e

θθ

from the compatibility equation (10.7). This equation and the equation

of motion (10.3) then constitute two equations for the two unknown stress compo-

nents

θθ

. Eliminate

θθ

between these two equations to obtain a single second

order differential equation for

and then use the identity in Problem 10.9 to obtain

the general solution for

. Verify

that your ﬁnal expression agrees with equation

(10.21).

Section 10.4

10.11. The steel turbine disk of Problem 10.2 is to be drilled with a central hole

and shrunk on to a 100 mm diameter steel shaft with an interference such that the

interface pressure after assembly is 100 MPa.

Find the required radial interference

and the rotational speed in rpm at which

the disk will come loose from the shaft.

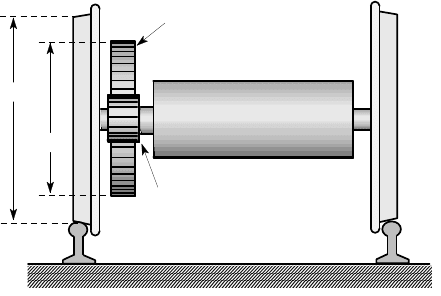
10.12. A wheel of inner radius a and outer radius na is shrunk on to a disk of radius a

with radial interference

. The material has Young’s modulus E and Poisson’s ratio

. Using the plane stress equations, ﬁnd the interface pressure after assembly and the

maximum tensile stress, which will be

θθ

at the inner radius of the wheel.

Obtain an approximate solution to the same problem assuming the disk is rigid

and using the thin-walled cylinder equations, as in the ‘Discussion’ following Exam-

ple 10.3. Sketch graphs of the results by each method as functions of n and identify

This is an alternative derivation of the general solution. These two methods of solution are

available for all elasticity problems. As in this problem, we can use the constitutive law

to express the compatibility equation in terms of stresses and then solve the equilibrium

and compatibility equations simultaneously. Alternatively, as in the text development, we

can use the strain-displacement relations and the constitutive law to express the stresses

in terms of the displacements and hence develop a statement of the equilibrium equation

in terms of displacements (see J.R. Barber (2010), Elasticity, Springer, Dordrecht, Nether-

lands, 3rd edn., §2.3). When we work in terms of displacements, the compatibility equation

is automatically satisﬁed.

482 10 Thick-walled Cylinders and Disks

the range of values of n for which the approximate result is within ±30% of the more

exact solution.

10.13. A steel cylinder of outside diameter 180 mm is shrunk on to a tungsten carbide

liner of outside diameter 60 mm and wall thickness 7.5 mm. If the stress in the liner

is to remain compressive when an internal pressure of 110 MPa is applied to it, what

must be the initial circumferential stress due to interference at the inside surface of

the liner?

Assume that axial stresses

are negligible. For tungsten carbide, E =600 GPa,

=0.21; for steel, E =210 GPa,

=0.3.

10.14. In the ANSI listings of limits and ﬁts, the tightest ﬁt suggested for mounting

a high grade cast iron gear on a steel shaft is FN2. For a nominal shaft diameter of

4.5 in, the tolerances permit the hole diameter to be anywhere in the range 4.5000 to

4.5014 in and the shaft external diameter to be in the range 4.5030 to 4.5039 in.

Suppose the gear outside diameter is 8 in and we have the bad luck to combine the

smallest permitted hole with the largest permitted shaft. What will be the maximum

tensile stress in the cast iron?

For cast iron, E =15×10

psi,

=0.25; for steel, E =30×10

psi,

=0.3.

10.15. Each axle of an electric freight locomotive supports a load of 44,200 lb on

two wheels with a 42 in effective diameter (see Figure P10.15). A gear of 63 teeth

and 31.5 in pitch diameter on the axle is driven by a steel pinion of 16 teeth and 8 in

pitch diameter on the steel shaft of an electric motor hung between the wheels. The

teeth are 1.12 in high on a root (dedendum) diameter of 7 in.

all dimensions in inches

Figure P10.15

The pinion is bored with a hole of 5 in diameter and is 6 in long. It is proposed to

press this onto the motor shaft without keying. The minimum coefﬁcient of friction

at the interference ﬁt is expected to be 0.1, which is low because of the lubricant used

in the pressing operation.

31.5

gear

pinion

motor

Problems 483

The maximum tractive force which can be developed at the wheel-rail contact

corresponds to 35% adhesion — i.e. to a friction coefﬁcient of 0.35 between the

wheel and the rail.

(i) Determine the interference pressure, the diametral interference and the assembly

force required if there is to be a safety factor of 3.33 against slipping in service.

(ii) What is the maximum tensile stress and the maximum shear stress in the pinion?

(iii) If a shrink ﬁt is used instead of pressing, what change of temperature is required

if the pinion is to be slipped over its shaft with a diametral clearance of 0.003 in.

(For steel, E =30×10

psi,

=0.3,

=6.3×10

−6

per

F.)

10.16. Figure P10.16 shows the cross section of a compound cylindrical pressure

vessel, fabricated by shrinking the outer cylinder onto the inner cylinder, so as to

leave a favourable state of prestress. Both cylinders are made of the same material.

It is desired to optimize the interference ﬁt such that when the vessel is loaded by a

gradually increasing internal pressure, the yield condition is reached simultaneously

at the inner surface of the inner cylinder and at the inner surface of the outer cylinder.

What should be the value of the interface pressure after assembly if the uniaxial yield

stress for the material is S

Figure P10.16

Section 10.5

10.17. A thin disk of inner radius a/3 and outer radius a rotates about its axis at speed

Ω

. The inner radius is traction free and the outer radius carries turbine blades which

exert an average tensile traction

due to centrifugal effects when the rotational

speed is

Ω

Show that the disk becomes fully plastic at a speed given by

Ω



Ω



484 10 Thick-walled Cylinders and Disks

where S

is the yield stress in uniaxial tension and the material obeys Tresca’s yield

criterion.

10.18*. Due to defects in the microstructure, a certain material has the biaxial yield

surface shown in Figure P10.18, where S

is the yield stress in uniaxial tension.

( , )

( )

Figure P10.18

The material is used to construct a thick-walled axisymmetric pressure vessel of

inner radius a and outer radius b, which will be subjected to internal pressure p. The

vessel is tested by increasing the pressure until all the material has yielded — i.e. the

conditions are fully plastic. Find the value of p needed to achieve complete plasticity

and the corresponding distribution of radial and circumferential stress.

Assume that the axial stress

(which is the third principal stress

) has no

effect on the yield surface in the range in question.

10.19. A thin circular disk of inner radius a and outer radius na carries blading at

its circumference which imposes there a tensile traction of ka

Ω

, where

Ω

is the

rotational speed. Find expressions for (i) the speed at which ﬁrst yield occurs and (ii)

the speed at which the disk becomes fully plastic. Find the ratio of these values for

the case where n= 2 and

=0.3. Comment on your result.

10.20. Find the rotational speed at which the turbine disk of Problem 10.2 becomes

fully plastic, if the steel has a uniaxial yield stress S

=700 MPa.