Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.

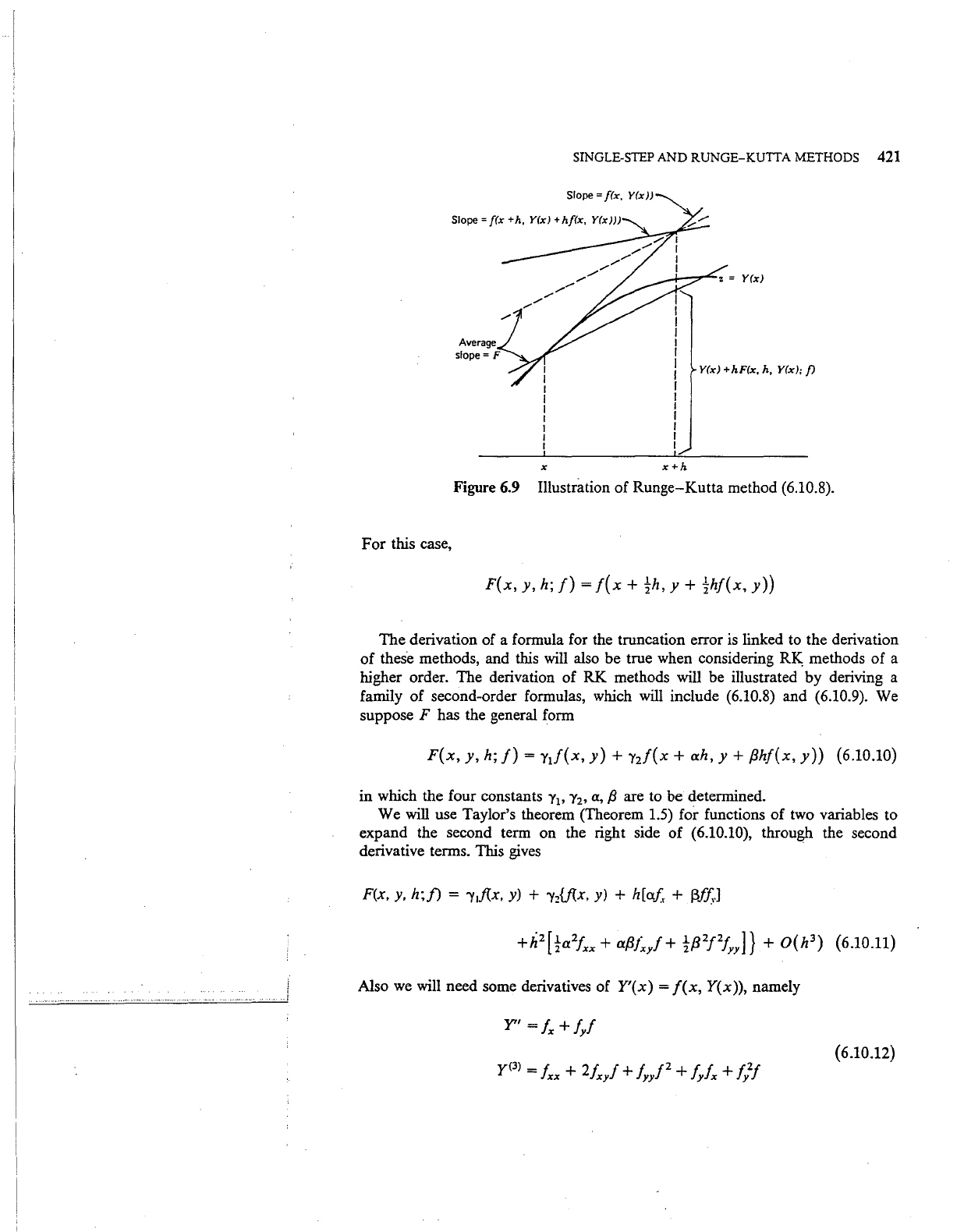
For this case,
SINGLE-STEP
AND
RUNGE-KUTTA
METHODS 421
Slope=
[(x,
Y(x))
Slope=
f(x
+h,
Y(x)
+h[(x,
Y(x)))
Average
slope=
F
X
Y(x)
+hF(x,
h,
Y(x);
fJ
x+h
Figure 6.9 Illustration of Runge-Kutta method (6.10.8).
F(x,
y,
h;
f)=
f(x
+
th,
Y +
thf(x,
y))
The derivation of a formula for the truncation error
is
linked to the derivation
of
these methods, and this will also be true when considering
RI\
methods of a
higher order. The derivation of
RK
methods will be illustrated
by
deriving a
family of second-order formulas, which
will
include (6.10.8) and (6.10.9).
We
suppose F has the general form
F(x,
y,
h;
f)
=
Yd(x,
y)
+ y
2
f(x
+
ah,
y + f3hf(x, y
))
(6.10.10)
in which the four constants y
1
,
y
2
,
a,
f3
are to be determined.
We
will
use Taylor's theorem (Theorem 1.5) for functions of
two
variables to
expand the second term on the right side
of
(6.10.10), through the second
derivative terms. This gives
·
F(x, y,
h;f)
=
-y
1
f(x, y) +
"'(
2
{fix,
y)
+ h[af, +
13/f,.]
I Also
we
will need some derivatives of Y'(x) =
f(x,
Y(x)), namely
~==~~~==~====~~==~~/
{6.10.12)

I
J
422 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
For
the truncation error,
h2
h3
=
hY'
+ - Y" + -
y<
3
l
+
O{h
4
)-
hF(x
Y h·
f)
n 2 n 6 n
n• n•
•
Substituting from (6.10.11) and (6.10.12), and collecting together common powers
of
h, we obtain
All derivatives are evaluated at
(xn, Yn).
We wish to make the truncation error converge to zero
as
rapidly as possible.
The coefficient
of
h
3
cannot be zero
in
general,
iff
is allowed to vary arbitrarily.
The requirement that the coefficients
of
h and h
2
be
zero leads to
and this yields
1
""6/3
=-
2
The system (6.10.14)
is
underdetermined, and its general solution is
1
a=/3=-
2y2
{6;10.14)
{6.10.15)
with y
2
arbitrary. Both (6.10.8) (with y
2
= !) and (6.10.9) (with y
2
= 1) are
special cases
of
this solution.
By
substituting into (6.10.13),
we
can obtain the leading term in the truncation
error, dependent
on
only y
2
.
In
some cases, the value of y
2
has been chosen to
make the coefficient of h
3
as
small as possible, while allowing f to vary
arbitrarily.
For
example, if
we
write (6.10.13)
as
{6.10.16)
then the Cauchy-Schwartz inequality [see (7.1.8)
in
Chapter
7]
can
be
used to
show
(6.10.17)

SINGLE-STEP AND RUNGE-KUTTA METHODS 423
where
(
)
-{(1
I
2)2
(1
/3)2
(I
1
/32)2
1
]1/2
C2
Yz
·-
6 - 2Y2a +
:;
- Y2a + 6 -
2Y2
+ i8
with a,
f3
given
by
(6.10.15).
The
minimum
value
of
c
2
(y
2
)
is
attained with
y
2
= .75,
and
c
2
(.75) =
1/118.
The
resulting second-order numerical method is
Yn+i
= Y, +
~
[!(x,,
y,)
+
3/(
x,
+
}h,
y,
+
}hf(x,,
y,))]
n
~
0
{6.10.18)
It
is
optimal
in the sense
of
minimizing the coefficient c
2
(y
2
)
of
the term c
1
(/)h
3
in
the
truncation
error.
For
an
extensive discussion
of
this means
of
analyzing the
truncation
error
in RK methods, see Shampine (1986).
Higher
order
formulas
can
be
created
and
analyzed
in
an
analogous manner,
although
the
algebra becomes very complicated. Assume a formula for
-F(x,
y,
h;
f)
of
the form
p
F(x,
y,
h;
/)
= L Y}'}
j~l
vi=
f(x,
y)
(6.10.19)
j = 2,
...
, p (6.10.20)
These
coefficients
can
be
chosen
to
make
the
leading
terms
in
the truncation error
equal
to
zero,
just
as was
done
with (6.10.10)
and
(6.10.14). There is obviously a
connection
between the
number
of
evaluations
of
f(x,
y),
call
it
p,
and
the
maximum
possible
order
that
can
be
attained
for the
truncation
error. These are
given
in
Table
6.23, which is
due
in
part-to
Butcher
(1965).
Until
about
1970,
the
most
popular
RK
method
has
probably
been the
original classical formula
that
is a generalization
of
Simpson's
rule.
The
method
is
h
Yn+i
=
Yn
+
6[v;.
+
2V2
+
2Vj
+
V.S]
(6.10.21)
vl
=
f(x,,
y,)
V
2
=t(x,
+
~h,
y,
+
~hV
1
)
Vj =
t(
x,
+
~h,
y,
+
~hV
2
)
V.S
=
f(x,
+
h,
Yn
+ hf.J)
'
I
I
I
I
424 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
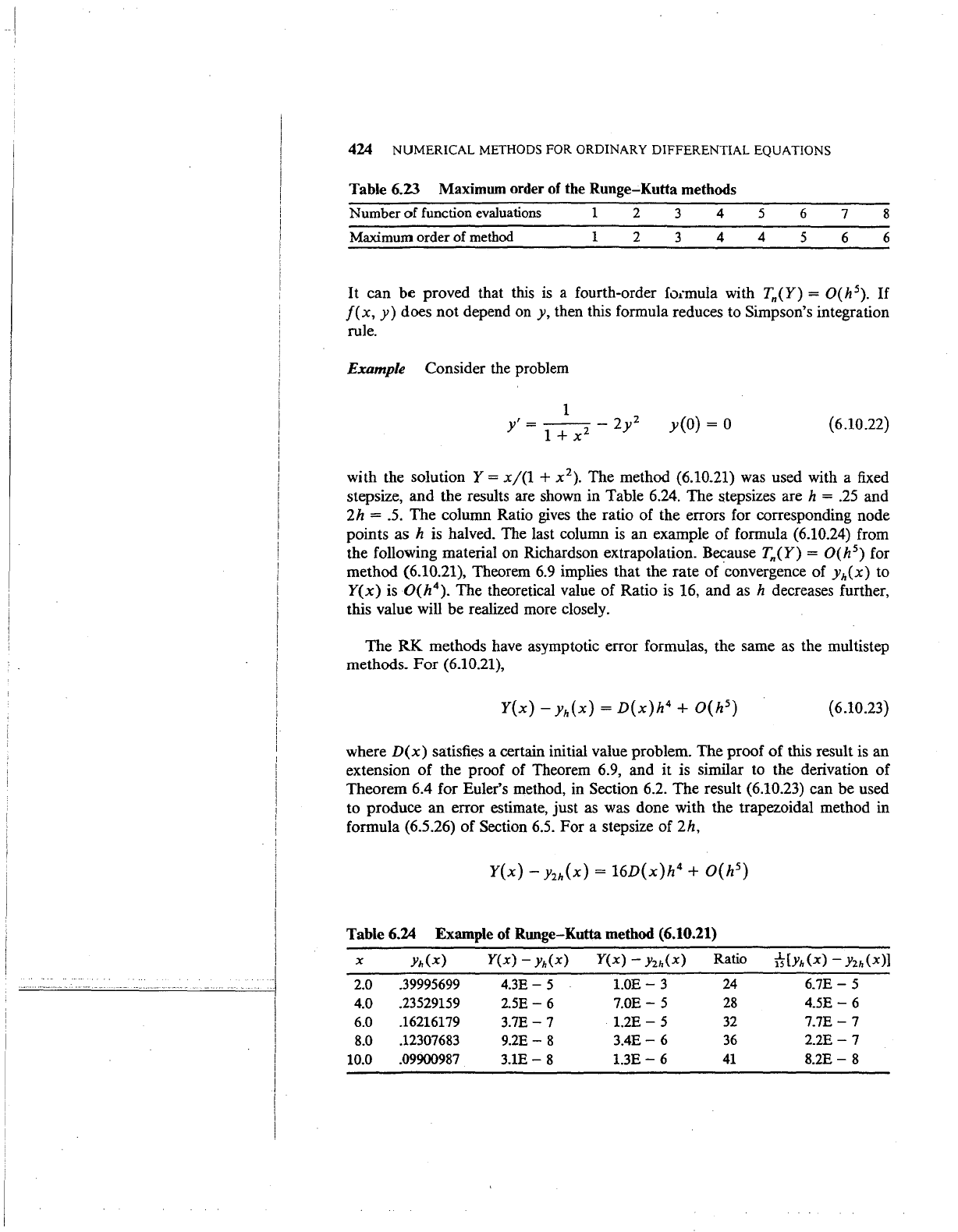
Table 6.23 Maximum order of the Runge-Kutta methods
Number of function
evaluations
1 2 3 4 5
6
7 8
Maximum order of
method
1 2 3 4 4
5
6
6
It can
be
proved that this is a fourth-order foimula with Tn(Y) = O(h
5
).
If
j(x,
y)
does
not
depend on y, then this formula reduces to Simpson's integration
rule.
Example Consider the problem
1
y'=
---2y2
1 + x
2
y(O)
= 0 (6.10.22)
with the solution Y =
xj(1
+ x
2
).
The
method (6.10.21) was used with a fixed
stepsize, and the results are shown in Table 6.24.
The
stepsizes are h = .25 and
2h = .5.
The
column Ratio gives the ratio of the errors for corresponding node
points
as
h is halved. The last column is an example
of
formula (6.10.24) from
the following material on Richardson extrapolation. Because
Tn(Y) =
O(h
5
)
for
method
(6.10.21), Theorem 6.9 implies that the
rate
of
convergence of
yh(x)
to
Y(x)
is
O(h
4
).
The
theoretical value
of
Ratio is 16,
and
as h decreases further,
this value will
be
realized more closely.
The
RK
methods have asymptotic error formulas, the same as the multistep
methods.
For
(6.10.21),
{6.10.23)
where
D(x)
satisfies a certain initial value problem.
The
proof
of
this result is an
extension
of
the proof of Theorem 6.9, and
it
is similar to the derivation
of
Theorem 6.4 for Euler's method, in Section 6.2.
The
result (6.10.23) can
be
used
to
produce
an
error estimate,
just
as was done with the trapezoidal method in
formula (6.5.26)
of
Section 6.5.
For
a stepsize
of
2h,
Table 6.24
Example of Runge-Kutta method (6.10.21)
X
Yh(x)
Y(x)-
Yh(x)
Y(x)
- Yzh(x)
Ratio
i5-[yh(x)-
Yzh(x)]
2.0 .39995699
4.3E-
5
l.OE-
3
24
6.7E-
5
4.0 .23529159
2.5E-
6
7.0E-
5
28
4.5E-
6
6.0
.16216179
3.7E-
7
1.2E-
5
32
7.7E-
7
8.0
.12307683
9.2E-
8
3.4E-
6
36
2.2E-
7
10.0
.09900987
3.1E-8
1.3E-6
41
8.2E-
8

SINGLE-STEP AND
RUNGE-KUTTA
METHODS
425
Proceeding
as
earlier for (6.5.27),
we
obtain
(6.10.24}
and the first term on the right side is an estimate of the left-hand error. This
is
illustrated in the last column of Table
6.24.
Convergence analysis In order to obtain convergence of the general schema
(6.10.4),
we
need to have T,(Y)
-+
0 as h
-+
0. Since
Y(x,+
1
)
-
Y(x,)
T,(Y) = h -
F(x,,
Y(x,),
h;
f)
we require that
F(x,
Y(x),
h;
f)-+
Y'(x) =
f(x,
Y(x))
as
h-+0
More precisely, define
8(h) =
and assume
Max
· 1/(x,
y)-
F(x,
y, h;
f)
I
x
0
S JCS
b
-oo<y<oo
8(h)-+
0
as
h-+0
(6.10.25)
(6.10.26}
This is occasionally called the consistency condition for the RK method (6.10.4).
We will also need a Lipschitz condition on
F:
IF(x,
y,
h;
/)-
F(x,
z,
h;
!)I~
Ljy-
zj
(6.10.27}
for all x
0
~
x
~
b, -
oo
<
y,
z <
oo,
and all small h >
0.
This condition
is
usually proved by using the Lipschitz condition (6.2.12) on
f(x,
y).
For example,
with method
(6.10.9},
jF(x,
y,
h;
/)-
F(x,
z,
h;
f)
I
=/I(
x +
~·
y +
~f(x,
y))-
1(
x +
~'
z +
~f(x,
z))
I
S
1y-
z +
~[J(x,
y)-
f(x,
z)] I
s
x(1
+~K
)IY-
zl
Choose L =
K(l
+
}K}
for h
~
1.

i
I
i
I
I
I
426 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
Theorem 6.9 Assume that the Runge-Kutta method (6.10.4) satisfies the
Lipschitz condition
(6.10.27). Then for the initial value problem
(6.10.1), the solution {
Yn}
satisfies
(6.10.28)
where
T
(h)
=
Max
1-r,
(
Y)
I (6.10.29)
x
0
sx.sh
_
If
the consistency condition (6.10.26)
is
also satisfied. then the
numerical solution {
Yn}
converges to
Y(
x
).
Proof Subtract (6.10.4) from (6.10.7) to obtain
in which
en=
Y(xn)
-
Yn·
Apply the Lipschitz condition ·(6.10.27) and
use
(6.10.29) to obtain
Xo
.=:;;
XN
.=:;;
b (6.10.30)
As with the convergence proof for the Euler method. this leads easily to
the result
(6.10.28) [see (6.2.20)-(6.2.22)].
In
most
cases,"
it
is
known by direct computation that T(
h)
~ 0 as
h
~
0, and in that case, convergence of {
Yn}
to
Y(x)
is immediately
proved. But all that
we
need to know
is
that (6.10.26)
is
satisfied. To see
this, write
Thus
T(h)
~
0
ash~
0,
completing the proof.
•
The following result
is
an immediate consequence of (6.10.28).

SINGLE-STEP
AND
RUNGE-KUTIA
METHODS 427
Corollary
If
the Runge-Kutta method (6.10.4) has a truncation error
T,,(
Y)
=
O(hm+
1
),
then the rate of convergence of
{.Yn}
to
Y(x)
is
O(hm) .
•
It
is not too difficult to derive an asymptotic error formula for the
Runge-Kutta
method (6.10.4), provided one is known for the truncation error. Assume
(6.10.31)
with cp(x) determined by
Y(x)
and
f(x,
Y(x)). As
an
example see the result
(6.10.13) to obtain this expansion for second-order
RK
methods. Strengthened
forms
of
(6.10.26) and (6.10.27) are also necessary. Assume
BF(x,
y,
h;!)
(
2
)
F(
x,
y, h;
f)
-
F(
X,
z, h;
j)
= B ( y - z) + 0 ( y -
z)
.Y
(6.10-.32)
and
also that
I
BJ(x,y)
BF(x,y,h;/)1
o
1
(h) = Max a -
~
0
x
0
5.x5.h
Y
By
-oo<y<c:o
(6.10.33)
In practice,
both
of
these results are straightforward to confirm. With these
assumptions, we can derive the formula
(6.10.34)
with
D(x)
satisfying the linear initial value problem
D' =
f_v(x,
Y(x))D(x)
+ cp(x)
(6.10.35)
Stability results can be given for
RK
methods, in analogy with those for
multistep methods. The basic type
of
stability, defined near the beginning
of
Section 6.8, is easily proved.
The
proof is a simple modification
of
that
of
(6.2.29), the stability
of
Euler's method, and we leave
it
to Problem 49.
An
essential difference with the multistep theory is
that
there -are no parasitic
solutions created by the
RK
methods; thus the concept
of
relative stability does
not
apply
to
RK
methods. The regions
of
absolute stability can be studied as
1
with the multistep theory,
but
we omit
it
here, leaving it to the problems.
•"_.I
Estimation
of
the truncation error
In
order to control
the
size
of
the truncation
error, we must first
be
able to estimate it. Let
un(x)
denote the solution
of
y'
=
f(x,
y)
passing through (xn•.Yn) [see (6.5.9)]. We wish to estimate the error
in Yh(xn +
2h)
relative to un(xn + 2h).

)
i
I
I
,I
428 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
Using (6.10.30) for the error in
Y~r(x)
compared to
u,(x),
and using the
asymptotic formula (6.10.31),
u,(xj+l)
-
Y~r(xj+r)
=
u,(xj)-
Y~r(x)
From
this,
it
is straightforward to prove
u,(x,
+h)-
Y~r(x,
+h)=
cp,(x,)hm+l + O(hm+Z)
u,(x,
+
2h)-
ylr(x, +
2h)
=
2cp,(x,)hm+l
+ O(hm+Z)
Applying the same procedure to
Yz~r(x),
From
the last two equations,
u,(x,
+
2h)-
Y~r(x,
+
2h)
1
=
2
m_
1
[ylr(x, +
2h)
-
Yzh(x,
+ 2h)J- + O(hm+Z) (6.10.36)
and
the first term on the right is an asymptotic estimate of the error on the left
side.
Consider the computation of
Y~r(x,
+
2h)
from
Y~r(x,)
=
y,
as a single step in
an
algorithm. Suppose that a user has given an error tolerance
t:
and
that the
value
of
1 .
trunc =
u,(x,
+
2h)-
y"(x,; +
2h)
=
2
m_
1
[Y~r(x,
+
2h)-
Yz~r(x,
+
2h)]
(6.10.37)
is
to
satisfy
(6.10.38)
This controls the error per unit step
and
it requires that the error
be
neither too
large
nor
too small. Recall
the
concept
of
error
per
unit
stepsize in (6.6.1)
of
Section 6.6.
If
the test is satisfied, then computation continues with the same
h.
But if it is
not
satisfied, then a new value h must be chosen. Let it
be
chosen by

SINGLE-STEP AND RUNGE-KUTTA METHODS 429
where !Jln(xn)
is
determined from ·
trunc
IPn(xJ = 2hm+1
With the new value of
h,
the
new
truncation error should lie near the midpoint
of
(6.10.38). This form of algorithm has been implemented with a number of
methods.
For
example, see Gear (1971, pp.
83-84)
for a similar algorithm for a
fourth-order
RK
method.
With many programs, the error estimation
(6.10.37)
is
added to the current
calculated value of
yh(xn +
2h),
giving a more accurate result. This
is
called local
extrapolation. When it
is
used, the error per unit step criterion of (6.10.38)
is
replaced by an error per step criterion:
(6.10.39)
In such cases, it can be shown that the local error in the extrapolated value of
Yh(xn +
2h)
satisfies a modified error per unit step criteria [see Shampine and
Gordon
(1975), p. 100]. For implementations of the same method, programs that
use local extrapolation and the error per step criterion appear to be more efficient
than those using
(6.10.38) and not using local extrapolation.
To
better understand the expense of RK methods with the error estimation
previously given, consider only fourth-order
RK
methods with four evaluations
of
f(x,
y)
per
RK
step. In going from xn to
xn
+
2h,
eight evaluations will be
required to obtain
Yh(xn +
2h),
and three additional evaluations to obtain
Y2h(xn +
2h).
Thus a single step of the variable-step algorithms will require
eleven evaluations of
f-
Although fairly expensive
to
use when compared with a
multistep method, a variable-stepsize RK method
is
very stable, reliable, and
is
comparatively easy to program for a computer.
Runge-Kutta-Fehlberg methods The Runge-Kutta-Fehlberg methods are
RK
methods.in.which the truncation error
is
computed by comparing the computed
answer
Yn+I
with the result
ofan
associated higher order··RKformula.The most
popular of such methods are due to
E.
Fehlberg, [e.g., see Fehlberg (1970)]; these
are currently the most popular RK methods. To clarify the presentation, we
consider only the most popular pair of Runge-Kutta-Fehlberg (RKF) formulas
of order 4 and
5.
These formulas are computed simultaneously, and their
difference is taken as an estimate of the truncation error in the fourth-order
method.
Note from Table
6.23 that a fifth-order RK method requires six evaluations
of
f per step. Consequently, Fehlberg chose to use
five
evaluations of f for the
fourth-order formula, rather than the usual four. This extra degree of freedom
in
choosing the fourth-order formula allowed
it
to be chosen with a smaller
truncation error, and this
is
illustrated later.
As before, define
j = 2,
...
,6
(6.10.40)
-1
I
430
NUMERICAL
METHODS FOR
ORDINARY
DIFFERENTIAL
EQUATIONS
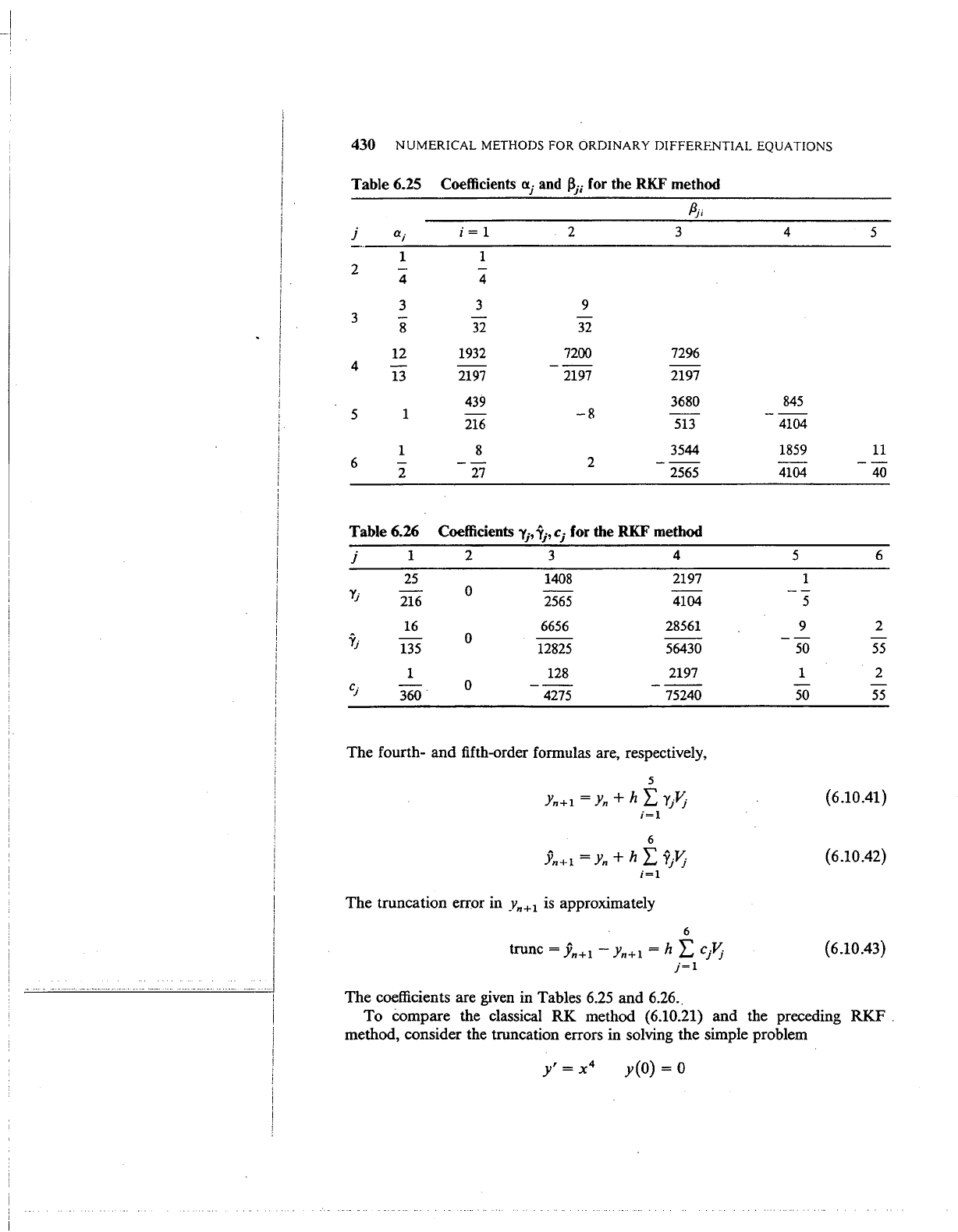
Table 6.25 Coefficients
a.i
and
f3i;
for the RKF method
flji
j
a;
i=1
2 3
1
1
2
4
4
3
3 9
3
8
32
32
12
1932
7200
7296
4
13
2197
2197
2197
439
3680
5
1
216
-8
513
1 8
3544
6
2
27
2
2565
Table 6.26
Coefficients
yi,
ii,
ci
for the RKF method
j
1 2 3
4
25
1408
2197
YJ
216
0
2565
4104
16
6656
28561
.YJ
-
0
--
135
12825
56430
1
128
2197
cJ
-
0
---
360.
4275
75240
The fourth- and fifth-order formulas are, respectively,
5
Yn+l=yn+hL'Yj~
i=l
6
Yn+l
=
Yn
+ h L
Yj~
i=l
The truncation error in
Yn+I
is
approximately
6
trunc =
Yn+l
-
Yn+l
= h L
Cj~
j=l
The coefficients are
given
in Tables
6.25
and
6.26
..
4
5
845
4104
1859
11
4104
40
5
6
1
--
5
9 2
--
-
50
55
1 2
-
-
50
55
(6.10.41)
(6.10.42)
(6.10.43)
To
compare the classical
RK
method (6.10.21) and the preceding
RKF
.
method, consider the truncation errors in solving the simple problem
y(O)
= 0
