Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.

SINGLE-STEP AND
RUNGE-KUTIA
METHODS 431
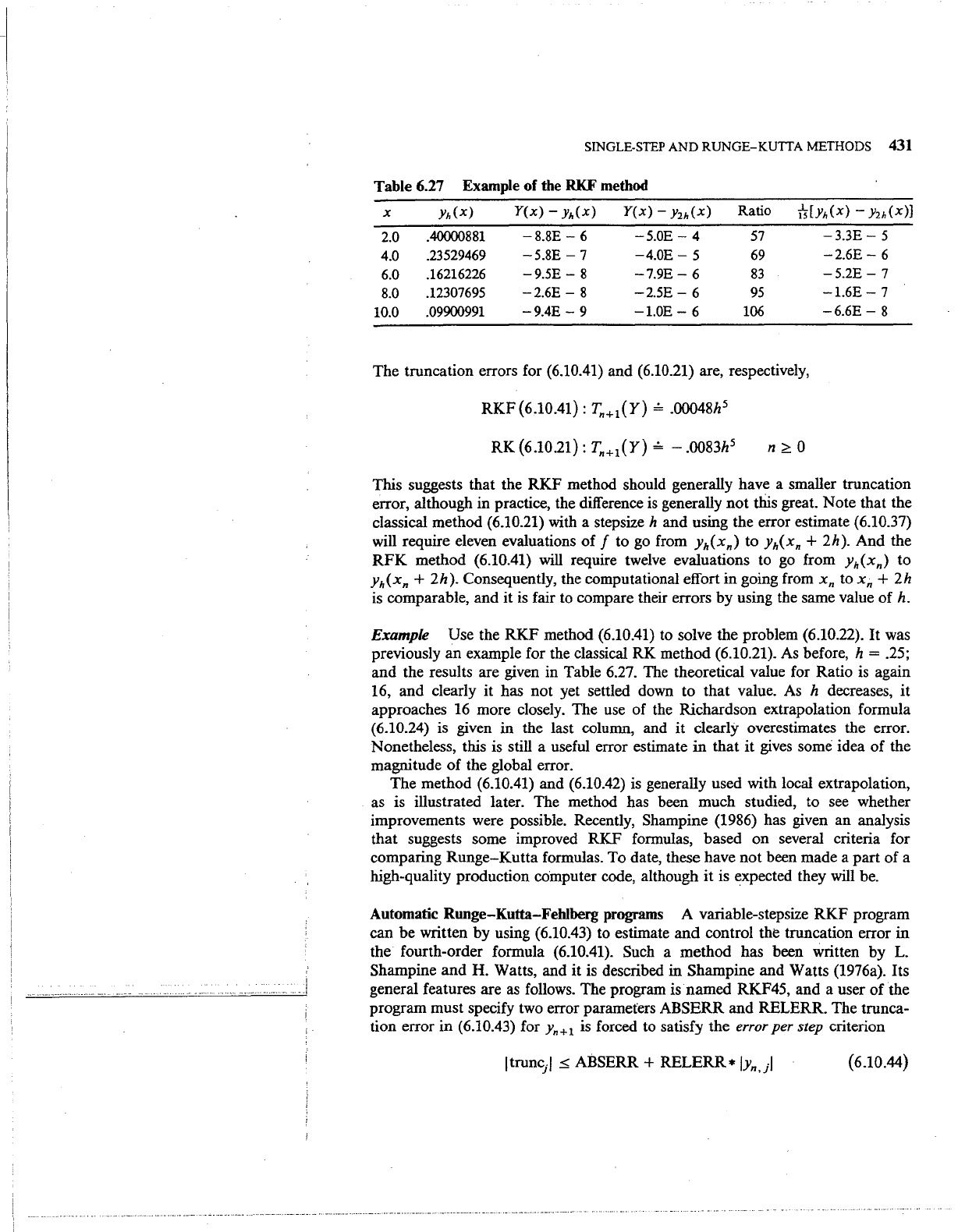
Table 6.27
Example of the
R.KF
method
X
Yh(x)
Y(x)-
Yh(x)
Y(x)-
Y2h(x)
Ratio
f5-[yh(x)-
Y2h(x)]
2.0
.40000881
-8.8E-
6
-5.0E-
4
57
-3.3E-
5
4.0
.23529469
-5.8E-
7
-4.0E-
5
69
-2.6E-
6
6.0
.16216226
-9.5E-
8
-7.9E-
6
83
-5.2E-
7
8.0
.12307695
-2.6E-
8
-2.5E-
6
95
-1.6E-
7
10.0
.09900991
-9.4E-
9
-l.OE-
6
106
-6.6E-
8
The
truncation errors for (6.10.41) and (6.10.21) are, respectively,
RKF(6.10.41):
T,+
1
(Y)
~
.00048h
5
RK
(6.10.21):
Tn+l
(Y)
~
- .0083h
5
n
~
0
This suggests that the
RKF
method should generally have a smaller truncation
error, although in practice, the difference is generally
not
tliis great. Note that the
classical method (6.10.21) with a stepsize
h and using the error estimate (6.10.37)
will require eleven evaluations
off
to go from Yh(xn) to Yh(xn + 2h). And the
RFK
method (6.10.41) will require twelve evaluations to go from Yh(xn)
to
yh(xn + 2h). Consequently, the computational effort in going from xn to xn +
2h
is comparable, and
it
is fair to compare their errors
by
using the same value of h.
Example
Use the
RKF
method (6.10.41) to solve the problem (6.10.22).
It
was
previously
an
example for the classical
RK
method (6.10.21). As before, h = .25;
and
the results are given in Table 6.27. The theoretical value for Ratio is again
16, and clearly it has
not
yet settled down to that value. As h decreases,
it
approaches 16 more closely. The use of the Richardson extrapolation formula
(6.10.24) is given in the last column, and
it
clearly overestimates the error.
Nonetheless, this is still a useful error estimate
in
that
it
gives some idea
of
the
magnitude
of
the global error.
The
method (6.10.41) and (6.10.42) is generally used with local extrapolation,
as is illustrated later. The method has been much studied, to see whether
improvements were possible. Recently, Shampine (1986) has given an analysis
that suggests some improved
RKF
formulas, based on several criteria for
comparing
Runge-Kutta
formulas. To date, these have
not
been made a
part
of
a
high-quality production computer code, although
it
is expected they will be.
Automatic Runge-Kutta-Fehlberg programs A variable-stepsize
RKF
program
can
be
written
by
using (6.10.43) to estimate
and
control the truncation error
in
the fourth-order formula (6.10.41). Such a method has been written by L.
Shampine
and
H. Watts, and
it
is described in Shampine and Watts (1976a). Its
general features are
as
follows. The program is
named
RKF45, and a user
of
the
program must specify two error parameters ABSERR and RELERR. The trunca-
tion error
in
(6.10.43) for
Yn+l
is forced to satisfy the error per step criterion
jtruncjj
~
ABSERR +
RELERR•
IYn,)
(6.10.44)

432 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
for each component
Yn,
j of the computed solution
Yn
of the system of differential
equations being solved. But then the final result of the computation, to be used in
further calculations,
is
taken to be the fifth-order formula
Yn+I
from (6.10.42)
rather than the fourth-order formula
Yn+I·
The terms
Yn
on the right side in
(6.10.41) and (6.10.42) should therefore
be
replaced by
Yn·
Thus RKF45 is really
a fifth-order method, which chooses the stepsize
h by controlling the truncation
error
in
the fourth-order formula (6.10.41). As before, this
is
called local
extrapolation, and it can be shown that the bound (6.10.44) for
Yn+l
will imply
that
Yn+I satisfies a modified error per unit stepsize bound on its truncation
error. The argument
is
similar to that given in Shampine and Gordon (1975, p.
100) for variable-order Adams methods.
The tests of Shampine et al. (1976) show that RKF45 is a superior
RK
program, one that
is
an excellent candidate for inclusion in a library of programs
for solving ordinary differential equations. It has become widely used, and
is
given
in
several texts [e.g., Forsythe et al. (1977), p. 129].
In
general, the comparisons given in Enright and Hull (1976) have shown
RKF
methods to be superior to other
RK
methods. Comparisons with multistep
methods are more difficult. Multistep methods require fewer evaluations of the
derivative
f(x,
y)
than RK methods, but the overhead costs per step are much
greater with multistep than with
RK
methods. A judgment as to which kind of
method to use depends on how costly it is to evaluate
f(x,
y)
as compared with
the overhead costs in the multistep methods. There are other considerations, for
example, the size of the system of differential equations being solved. A general
discussion of these factors and their influence is given in Enright and Hall (1976)
and Shampine et
al.
(1976).
Example Solve the problem
y(O)
= 1
which has the solution
20
Y(x) =
(1
+
19e-xl4).
The problem was solved using RKF45, and values were output at x =
Table6.28
Example of Runge-Kutta-Fehlberg program RKF45
ABSERR =
10-
3
ABSERR = 10
6
ABSERR = 10
9
X
Error NFE
Error
NFE
Error
NFE
4.0
-1.4E-5
19
-2.2E-
7
43
-5.5E-
10
121
8.0
-3.4E-
5
31
-5.6E..,... 7
79
-1.3E-9
229
12.0
-3.7E-
5
43
-5.5E-
7
103
-8.6E-
10
312
16.0
-3.3E-
5
55
-5.4E-
7
127
-1.2E-
9
395
20.0
-1.8E-
6
67
-1.6E-
7
163
-4.3E-
10
503

i
..
I
BOUNDARY VALUE PROBLEMS
433
2,
4,
6,
...
,
20.
Three values of ABSERR
were
used, and RELERR =
10-
12
in
all
cases. The resulting global errors are
given
in Table 6.28. The column headed
by
NFE
gives the number of evaluations of
f(x,
y)
needed to obtain the
given
answer. Compare the results with those
given
in Table 6.15, obtained using the
yariable-order multistep program DDEABM.
A version of RKF45
is
available that estimates the global error in the
computed solution, using Richardson error estimation
as
in (6.10.24). For a
discussion of this code, called GERK,
see
Shampine and Watts (1976b), which
also contains a discussion of the general problem of global error estimation.
Jmplicit
Runge-Kutt:i methods
We
have considered only the explicit RK meth-
ods, since these are the main methods that are in current use. But there are
implicit RK formulas. Generalizing the explicit formula (6.10.19) and
(6.10.20),
we
consider ·
Yn+l
=
Yn
+ hF(xn,
Yn•
h;
/)
(6.10.45)
p
F(x,
y,
h;
f)=
L
r}j
j-1
j=1,
...
,p
(6.10.46)
The coefficients {
aj,
Pji•
"Yj}
specify the method. For an explicit method,
we
have
pji
= 0 for i
"2::.
j.
The implicit methods have been studied extensively in recent years, since some
of
them
possess stability properties favorable for solving stiff differential equa-
tions. For any order of convergence, there are A-stable methods of that order. In
this way, the implicit
RK
methods are superior to the multistep methods, for
which there are no A-stable methods of order greater than
2.
The most widely
used codes for solving stiff differential equations, at present, are based on the
backward differentiation formulas introduced in Section 6.9. But there
is
much
work on developing similar codes based on implicit
RK
methods. For an
introductory survey of this topic,
see
Aiken (1985,
Sec.
3.1).
6.11 Boundary Value Problems
Up to this point,
we
have considered numerical methods for solving only
initi~l
value problems for differential equations. For such problems, conditions on the
solution of the differential equation are specified
at
a single point, called the
initial point. We now consider problems in which the unknown solution has
conditions imposed on it at more than one point. Such problems for differential
equations are called boundary
value
problems, or
BVPs
for short.

434 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
A typical problem that
we
study
is
the two-point
BVP:
y"
=
f(x,
y,
y')
a<x<b
[
u(a)]
[u(b)]
['Y1]
A
u'(
a) + B u'( b) =
'Y2
(6.11.1)
The terms A and B denote given square matrices of order 2 X
2.
and y
1
and y
2
are given constants. The theory for
BVPs
such
as
this one
is
much more
complicated than for the
initial value problem (see Theorems
6.1
and 6.2 in
Section
6.1).
To
illustrate the possible difficulties,
we
give
the following examples.
Example 1. Consider the two-point linear
BVP
y"
=
-Ay
O<x<l
y(O)
= y(1) = 0
(6.11.2)
If
A is
not
one
of the numbers
(6.11.3)
then this BVP has the unique solution
Y(x)
=
0.
Otherwise, there are an infinite
number
of
solutions,
Y(x)
= C sin
(Ax)
with A chosen from (6.11.3) and
Can
arbitrary constant.
2.
Consider the related problem
y"
=
-Ay
+
g(x)
y(O)
= y(1) = 0
O<x<l
(6.11.4)
(6.11.5)
If
A is not chosen from (6.11.3), and if
g(x)
is continuous for
a~
x
~
b,
then
this problem has a unique solution
Y(x)
that
is
twice continuously differentiable
on
[0,
1].
In
contrast, if
A=
'1T
2
,
then the problem (6.11.5) has a solution if and
only if
g(
x)
satisfies
fg(x)sin('TTx)
dx = 0
Iri
the case that this is satisfied, the solution is given by
1
1
x
Y(x)
= Csin('TTx)
+-
g(t)sin('TT(x-
t))
dt
'1T
0
(6.11.6)
with C
an
arbitrary constant. A similar result holds for other A chosen from
(6.11.3).

i
···- f
BOUNDARY VALUE PROBLEMS 435
A
few
results from the theory of two-point
BVPs
is
now given, to help in
further understanding them and
to
aid in the presentation of numerical methods
for their solution.
We
begin with the two-point problem for the second-order
linear equation:
y"
=
p(x)y'
+
q(x)y
+
g(x)
a<x<b
[
u(a)]
[u(b)]
[''~]
A u'(a) + B u'(b) =
Y2
(6.11.7)
The
homogeneous problem
is
the case in which
g(x)
= 0 and y
1
,
y
2
=
0.
Theorem 6.10 The nonhomogeneous problem (6.11.7) has a unique solution
Y(x)
on
[a,
b], for each set of given
data
{g(x),
y
1
,
y
2
},
if and
only if the homogeneous problem has only the trivial solution
Y(x)
=
0.
Proof
See Stakgold (1979, p. 197). The preceding examples are illustrations
of
the theorem. •
For
conditions under which the homogeneous problem for (6.11.7) has only
the zero solution,
we
consider the following more special linear problem:
y"
=
p(x)y'
+
q(x)y
+
g(x)
a<x<b
(6.11.8)
a
0
y(a)-
a
1
y'(a)
= y
1
In
this problem,
we
say the boundary conditions are separated. Assume the
following conditions are satisfied:
q(x)
> 0
a:::;,x:::;,b
'(6.11.9)
lhol
+
lbd
* 0
Then the homogeneous problem for (6.11.8) has only the zero solution, Theorem
6.10
is
applicable, and the nonhomogeneous problem has a unique solution, for
each set
of
data
{g(x),
y
1
, y
2
}.
For a proof
of
this result, see Keller (1968, p. 11).
Example (6.11.5) illustrates this result.
It
also shows that the conditions (6.11.9)
are not necessary; the problem (6.11.5)
is
uniquely solvable for most negative
choices
of
q(x)
=.A.
The theory for the nonlinear problem (6.11.1)
is
far more complicated than
that for the linear problem (6.11.7). We give an introduction to that theory for
the following more limited problem:
y"
=
f(x,
y,
y')
a
0
y(a)-
a
1
y'(a)
= y
1
a<x<b
(6.11.10)

436 NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
The function f
is
assumed
to
satisfy the following Lipschitz condition:
if(x,
u
1
,
v) -
j(x,
u
2
,
v)
I~
Kju
1
-
u
2
j
if(x,
u,
v
1
)-
f(x,
u,
v
2
)
I~
Kiv
1
-
v
2
1
for all points
(x,
u;. v),
(x,
u,
v;) in the region
R = { (x,
u,
v
)Ia
~
x
~
b, -
oo
<
u,
v <
oo}
(6.11.11)
This
is
far stronger than needed, but it simplifies the statement of the following
theorem and the analysis of the numerical methods given later.
Theorem 6.11 For
the
problem (6.11.10), assume
f(x,
u,
v)
is
continuous on the
region
R and that it satisfies the Lipschitz condition (6.11.11). In
addition, assume that on
R, f satisfies
Bj(x,
u, v)
---->0
au
l
aj(x,u,v)l
av
~
M (6.11.12)
for some constant M >
0.
For the boundary conditions of
(6.11.10), assume
lao!
+
ibol
=F
0 (6.11.13)
Then the
BVP
(6.11.10) has a unique solution.
Proof See Keller (1968,
p.
9). The earlier uniqueness result for the linear
problem
(6.11.8)
is
a special case of this theorem. •
Nonlinear
BVPs
may be nonuniquely solvable, with only a finite number of
solutions. This
is
in contrast to the situation for linear problems, in which
nonuniqueness always
means an infinity of solutions, as illustrated in
(6.11.2)-(6.11.6). An example of such nonunique solvability is the second-order
problem
d [
dy]
dx
I(x)dx
+Asin(y)=O
O<x<l
y'(O) =
y'(l)
= 0,
I
y<x>
I
<1r
(6.11.14)
which arises
iii
studying the buckling of a column. The parameter A
is
propor-
tional to the load on the column; when
A exceeds a certain size, there
is
a
solution to the problem
(6.11.14) other than the zero solution.
For
further detail
on this problem,
see
Keller and Antman (1969, p. 43).
As with the earlier material
on
initial value problems [see (6.1.11)-(6.1.15)
in
Section 6.1], all boundary value problems for higher order equations can be

..
,
......
,j
BOUNDARY
VALUE
PROBLEMS
437
reformulated as problems for systems of first-order equations. The general form
of
a two-point BVP for a system of first-order equations
is
y' =
f{x,y)
a<x<b
{6.11.15)
Ay{a)
+
By(b)
= y
This
represents a system of n first-order equations.
The
quantities y(x), f(x,y),
andy
are
vectors with n components, and A and
Bare
matrices
of
order n X n.
There is a theory for such BVPs, analogous
to
that for the two-point problem
(6.11.1),
but
for reasons
of
space, we omit it here.
In
the
remainder of this section, we describe briefly the principal numerical
methods for solving the two-point
BVP (6.11.1). These methods generalize to
first-order systems such as
(6.11.15),
but
for reasons
of
space,
we
omit those
results.
Much
of
our
presentation follows Keller (1968), and
·a
theory for
first-order systems
is
given there. Unlike the situation with initial value problems,
it
.is
often advantageous to directly treat higher order BVPs rather than to
numerically solve their reformulation as a first-order system.
The
numerical
methods for the two-point problem are also less complicated to present, and
therefore we have opted to discuss the two-point problem rather than the system
(6.11.15).
Shooting methods One of the very popular approaches to solving a two-point
BVP is to reduce
it
to. a problem in which a program for solving initial value
problems
can
be used. We now develop such a method for the BVP (6.11.10).
Consider the initial value problem
y"
=
f(x,
y,
y')
a<x<b
( 6.11.16)
depending
on
the
parameters,
where c
0
,
c
1
.
are arbitrary constants satisfying
Denote the solution
of
(6.11.16)
by
Y(x;
s).
Then
it is straightforward to see that
for all
s for which Y exists.
Since Y is a solution of (6.11.1), all that is needed for it
to
be
a solution of
(6.11.10) is
to
have
it
satisfy the remaining
boundary
condition
at
b.
This means
that
Y(x;
s)
must satisfy
(6.11.17)
This is a
non~inear
equation for
s.
If
s*
is a root
of
'P(s), then
Y(x;
s*)
will satisfy

438
NUMERICAL METHODS FOR ORDINARY DIFFERENTIAL EQUATIONS
the
BVP
(6.11.10). It can be shown that under suitable assumptions on f and its
boundary conditions, the equation
(6.11.17)
will
have a unique solution s*
[see
Keller (1968),
p.
9).
We
can
use
a rootfinding method for nonlinear equations to
solve for
s*.
This
way
of finding a solution
to~
BVP
is
called a shooting method.
The name comes from ballistics,
in
which one attempts
to
determine the needed
initial conditions at
x = a in order to obtain a certain value at x =
b.
Any
of
the rootfinding methods of Chapter 2 can be applied
to
solving
cp(s) =
0.
Each evaluation
.of
cp(s)
involves the solution of the initial value
problem
(6.11.16) over [a, b
],
and consequently,
we
want
to
minimize the number
of such evaluations.
As
a specific example of an important and rapidly conver-
gent method,
we
look at Newton's method:
m =
0,1,
...
To
calculate
qJ'(s),
differentiate the definition (6.11.17) to obtain
where
aY(x;
s)
t(x)
=
as
To find
t(x),
differentiate
·the
equation
Y"(x;
s)
=
f(x,
Y(x;
s ),
Y'(x;
s ))
with respect to s. Then
~.
satisfies the initial value problem
g~(x)
= /
2
(x,
Y(x;
s),
Y'(x;
s)H.(x)
+/
3
(x,
Y(x;
s),
Y'(x;
s))~~(x)
(6.11.18)
(6.11.19)
(6.11.20)
(6.11.21)
The functions /
2
and f
3
denote the partial derivatives of
f(x,
u,
v)
with respect
to
u and
v,
respectively. The initial values are obtained from those
in
(
6.
11.16)
and
from
the definition of
g,.
In practice
we
convert the problems (6.11.16) and (6.11.21)
to
a system of four
first-order equations with the unknowns
Y,
Y',
t.
and
E:.
This system
is
solved
numerically, say with a method of order
p and stepsize
h.
Let
jh(x;
s)
denote
the approximation
to
Y(x; s), with a similar notation
for
the remaining un-
knowns. From earlier results for solving initial value problems, it can be shown
that these approximate solutions will be in error by
O(hP).
With suitable
assumptions on the original problem
(6.11.10), it can then be shown that the root
s:
obtained
will
also be in error
by
O(hP),
and
similarly for the approximate

BOUNDARY VALUE PROBLEMS 439
solution
yh(x;
st)
when compared to the solution
Y(x;
s*)
of
the boundary value
problem.
For
the details
of
this analysis, see Keller (1968, pp. 47-54).
Example
Consider the two-point BVP
2(y')2
y"
=
-y
+
--
y
-1
<X<
1
y(
-1)
=
y(1)
= ( e +
e-
1
)
-l
,;,
.324027137
(6.11.22)
The
true solution is
Y(x)
=(ex+
e-x)-
1
.
The initial value problem (6.11.15) for
the shooting method is
(2y')2
y"=
-y+
--
y
The
associated problem (6.11.21) for
~s(x)
is
-1<x::s;1
y'(
-1)
= s
~~(-1)=1
(6.11.23)
(6.11.24)
The
equation
for~~
uses the solution
Y(x;
s)
of
(6.11.23). The function
cp(s)
for
computing
s*
is given by
cp{s)
= Y(1;
s)-
(e +
e-
1
)-
1
For
use in defining Newton's method, we have
cp'(s)
=
~s(1)
From
the true solution
Yof
(6.11.22)
and
the condition
y'(
-1)
= s in (6.11.23),
the desired root s*
of
cp(
s)
is simply
e-
e-
1
s* =
Y'(
-1)
=
,;,
.245777174
(e+e-1)2
To
solve the initial value problem (6.11.23)-(6.11.24), we used the second-order
Runge-Kutta
method (6.10.9) with a stepsize
of
h =
2/n.
The
results for several
values
of
n are given in Table 6.29. The solution
of
(6.11.24) is denoted by
440 NUMERICAL
METH:ODS
FOR ORDINARY DIFFERENTIAL EQUATIONS
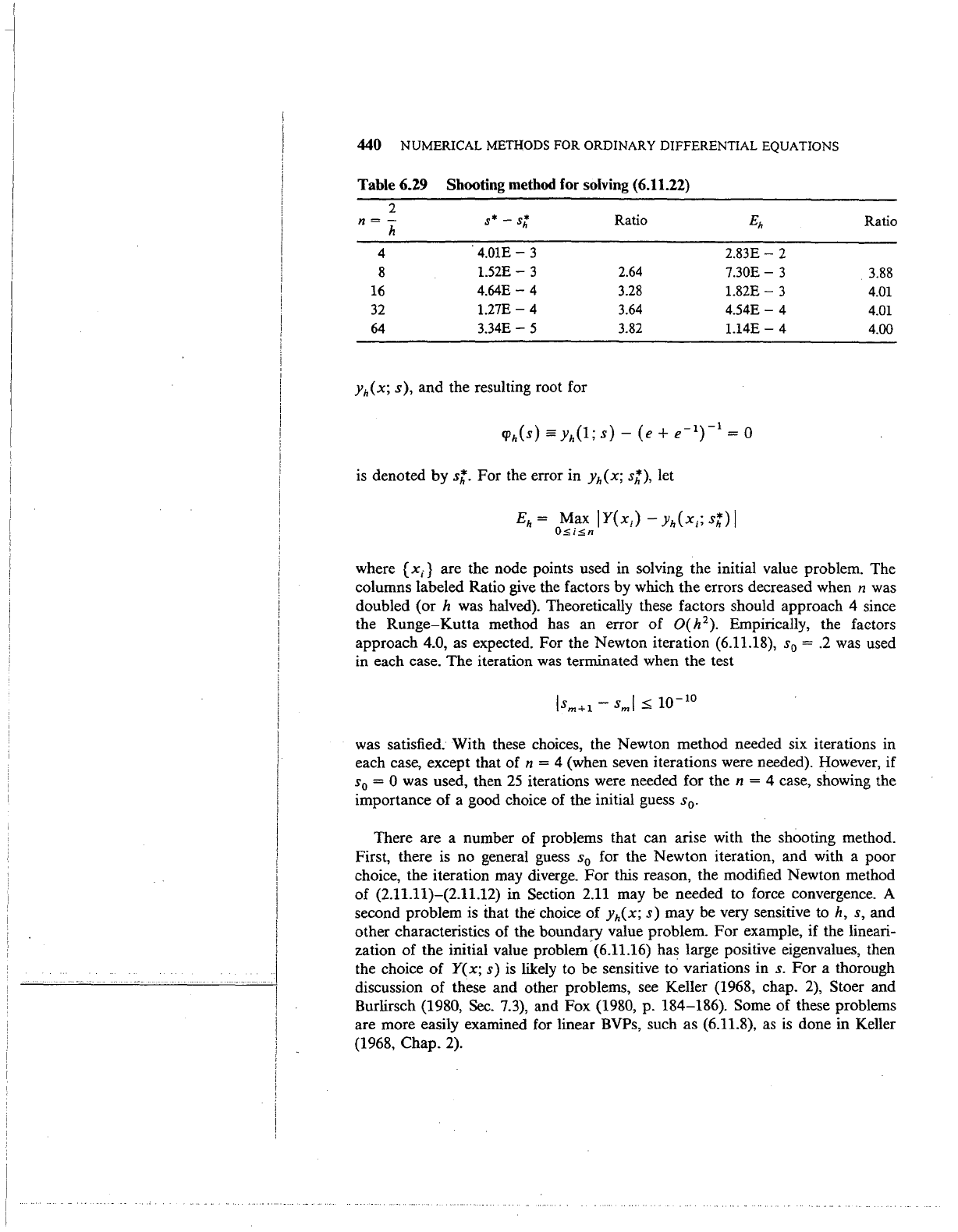
Table 6.29 Shooting method for solving (6.11.22)
2
n
=-
h
s*-
s:
Ratio
Eh
4
4.01E-
3
2.83E-
2
8
1.52E-
3
2.64
7.30E-
3
16
4.64E-
4
3.28
1.82E-
3
32
1.27E-
4
3.64
4.54E-
4
64
3.34E-
5
3.82
1.14E-
4
yh(x;
s),
and the resulting root for
is
denoted
by
s;.
For the error in
yh(x;
st),
let
Ratio
3.88
4.01
4.01
4.00
where
{X;}
are the node points used in solving the initial value problem. The
columns labeled Ratio
give
the factors by which the errors decreased when n was
doubled (or
h was halved). Theoretically these factors should approach 4 since
the
Runge-Kutta
method has an error
of
O(h
2
).
Empirically, the factors
approach
4.0, as expected. For the Newton iteration (6.11.18), s
0
=
.2
was used
in each case. The iteration
was
terminated when the test
was satisfied. With these choices, the Newton method needed six iterations in
each case, except that of
n = 4 (when seven iterations were needed). However, if
s
0
= 0 was used, then
25
iterations were needed for
then
= 4 case, showing the
importance of a good choice of the initial guess
s
0
.
There are a number of problems that can arise with the shooting method.
First, there
is
no general guess s
0
for the Newton iteration, and with a poor
choice, the iteration may diverge.
For
this reason, the modified Newton method
of (2.11.11)-(2.11.12) in Section
2.11
may be needed to force convergence. A
second problem is ihat the choice of
yh(x;
s) may be very sensitive to h, s, and
other characteristics of the boundary value problem. For example, if the lineari-
zation of the initial value
problem-(6.11.16) has large positive eigenvalues, then
the choice
of
Y(x;
s)
is
likely to be sensitive to variations in
s.
For
a thorough
discussion of these and other problems, see Keller (1968, chap.
2),
Stoer and
Burlirsch
(1980,
Sec.
7.3),
and Fox (1980, p. 184-186). Some of these problems
are more easily examined for linear
BVPs, such as (6.11.8), as
is
done
in
Keller
(1968, Chap. 2).
