Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


4 ERROR: ITS SOURCES, PROPAGATION, AND ANALYSIS
In particular, there are points
~
and
:X
in
[a,
b]
for which
m =
/(~),
M =
J(x)
Theorem 1.2 (Mean Value) Let
/(x)
be continuous for
a::;;
x::;;
b, and let it be
differentiable for
a < x <
b.
Then there is at least one point
~
in
. (a,
b)
for which
/(b)-
/(a)=
/'(~)(b-
a)
Theorem 1.3 (Integral Mean Value) Let
w(x)
be
nonnegative~and
integrable
on
[a,
b], and let
f(x)
be continuous
on
[a,
b]. Then
Jbw(x}f(x)
dx =
/(~)
jbw(x)
dx
a a
for
some~
E
[a,
b].
These theorems are discussed in most elementary calculus textbooks,
and
thus
we omit their proofs.
Some implications of these theorems are examined in the
problems
at
the end of the chapter.
One
of
the most important tools of numerical analysis
is
Taylor's theorem and
the associated Taylor series.
It
is
used throughout this text. The theorem gives a
relatively simple method for approximating functions
f(x)
by polynomials,
and
thereby gives a method for computing
f(x).
Theorem
1.4
(Taylor's Theorem) Let
f(x)
have n + 1 continuous derivatives
ori
[a,
b]
for some n
~
0, and let
x,
x
0
E
(a,
b].
Then
.
f(x)
= Pn(x) + Rn+l(x)
(x-
x
0
)
Pn(x) = f(xo) +
1
! f'(xo)
(x-
xor
+ ... +
n!
J<n>(xo)
(
x-x
)n+l
----;--0--:---/
( n + 1) (
~)
(n
+
1}!
for some
~
between x
0
and x.
(1.1.1)
(1.1.2)
(1.1.3)
Proof
The
derivation
of
(1.1.1) is given in most calculus texts.
It
uses carefully
chosen integration by parts in the identity
/(x)
=/(x
0
)
+
jxf'(t)dt
Xo

J
MATHEMATICAL
PRELIMINARIES
5
repeating it n times to obtain (1.1.1)-(1.1.3), with the integral form of
the remainder R,.+
1
(x). The second form of
R,+
1
(x)
is obtained by
using the integral mean value theorem with
w(t)
=
(x
- t)". •
Using Taylor's theorem,
we
obtain the following standard formulas:
x2
x"
xn+l
ez = 1 + x + - + · · · + - +
e~•
2
n!
(n
+ 1)!
(1.1.4)
x2 x4
x2"
cos(x)
=
1--
+--
· · · +(
-1)"--
2!
4!
(2n)!
x2n+2
+(-1)"+1
(2n
+
2)!cos(~J
(1.1.5)
x3
xs
x2n-1
sin(x)
=
x--
+--
· · · +(
-1)"-
1
...,..-----,--
3!
5!
(2n - 1)!
x2n+l
+(
-1)"
(
2
n +
1
)!
cos(EJ
(1.1.6}
(1
+
x)"
= 1 +
(~)x
+
(;)x
2
+ ·
..
+(~)x"
(1.1.7}
with
(
a:)=
a:(a:-1);··(a-k+1)
k
k!.
k =
1,2,3,
...
for any real number a.
For
all
cases,
the unknown
point
~z
is located between x
and
0.
An
important
special case of (1.1.7) is
1
x"+
1
--
= 1 + x + x
2
+ · · ·
+x"
+
--
1-x
1-x
(l.l.8)
This is the case a = -
1,
with x replaced
by
-
x.
The remainder has a simpler
form than
in
(1.1.7); it is easily proved by multiplying
both
sides
of
(1.1.8) by
1 - x
and
then simplifying. Rearranging (1.1.8), we
obtain
the familiar formula
for
a finite geometric series:
1 -
xn+l
1 + x + x
2
+
···
+x"
=
---
1-x
x'i=1
(1.1.9)

6 ERROR: ITS SOURCES, PROPAGATION, AND ANALYSIS
Infinite series representations for the functions on the left side of (1.1.4)
to
(1.1.8) can be obtained by letting n
-+
oo.
The infinite series for (1.1.4) to (1.1.6)
converge for all
x,
and those for
(1.1.7)
and (1.1.8) converge for lxl <
1.
Formula (1.1.8) leads to the well-known infinite geometric series
1
00
--
=
[xk
1 - X
k-0
lxl
< 1
(1.1.10)
The
Taylor series of -any sufficiently differentiable function
f(x)
can be
calculated directly from the definition
(1.1.2), with
as
many terms included
as
desired. But because of the complexity of the differentiation of many functions
f(x),
it
is
often better to obtain indirectly their Taylor polynomial approxima-
tions Pn(x)
or
their Taylor series, by using one
of
the preceding formulas (1.1.4)
through (1.1.8).
We
give
three examples, all of which have simpler error terms
than if
(1.1.3) were used directly.
Example
1.
Let
f(x)
=
e-x
2
•
Replace x by
-x
2
in (1.1.4) to obtain
x4
x2n
x2n+2
_
x2
2 {
1
)
n {
1
)
n+
l t
e = 1 - X + - - · · · + - - + - e'x
2!
n!
(n
+ 1)!
with
-x
2
~~x~O.
2.
Let
/(
x)
= tan
-l
( x ).
Begin
by setting x = - u
2
in
(1.1.8)
Integrate over
[0,
x] to get
x3
xs
x2n+1
tan-l(x)
=
x-
3 +
5-
...
+(
-1)"-2n_+_1
u2n+2
+(
-l)n+llx
__
du
o 1 + u
2
Applying the integral mean value theorem
u2n+2
x2n+3 1
J:
1 + u
2
du = 2n + 3 . 1 +
g;
with
gx
between 0 and x.
(1.1.11)

I
I
MATHEMATICAL PRELIMINARIES 7
3. Let
f(x)
=
Jd
sin(xt)
dt. Using (1.1.6)
1[ x3t3 1
{xt)2n-1
f(x)
=fa
xt-
-3-!
+
...
+(-1r-
-:-(2-n---1):-!
n (xt)2n+1 l
+(-1)
(
2
n+
1
)!cos(~x
1
)
dt
n
x2j-1
x2n+1
"(
)j-1
(
)n
1
1
2n+1
()
f::l
-1
(2j)!
+
-1
(2n + 1)! 0 ( COS
~XI
dt
with
~x
1
between 0 and xt. The integral
in
the remainder
is
easily bounded by
1/(2n
+ 2);
but
we
can also convert it to a simpler form. Although it wasn't
proved, it can be shown that
cos(~x
1
)
is
a continuous function of
t.
Then
applying the integral mean value theorem
. n
x2j-1
x2n+1
f
sin(xt)
dt =
I:
(
-1)j-
1
-(
.)'
+ (
-1r
(
)'cos
Ux)
o
j=l
2;
. 2n + 2 .
for some
fx between 0 and x.
Taylor's theorem
in
two
dimensions Let
f(x,
y)
be a given function of the two
independent variables
x and y.
We
will
show how the earlier Taylor's theorem
can be extended to the expansion of
f(x,
y)
about a given point
(x
0
, y
0
).
The
results will easily extend to functions of more than two variables. As notation, let
L(x
0
,
y
0
;
x
1
, y
1
) denote the set of all points
(x,
y)
on the straight line segment
joining
(x
0
,
y
0
)
and
(xp
y
1
).
Theorem .1.5 Let
(x
0
,
y
0
)
and
(x
0
+ t y
0
+
TJ)
be given points, and assume
f(x,
y)
is
n + 1 times continuously differentiable for all (x,
y)
in
some neighborhood of
L(x
0
,
y
0
;
x
0
+ t y
0
+
TJ).
Then
f(xo
+ t Yo+
TJ)
n 1 [ a a
]j
=
f(xo.
Yo)+
L
-:-
1
~-a
+ 11-a
f(x,
Y)
·=l
).
X y x-xo
J
y-h
1 [ a a ]
n+
1 I
+
(n
+ 1)!
~ax
+
1J
ay
f(x,
y)
x-xo+ll~
{1.1.12)
y-yo+II1J
for some 0
.:5:
()
.:5:
1.
The point
(x
0
+
0~,
y
0
+
011)
is
an unknown
point on the line
L(x
0
,
y
0
;
x
0
+ t Yo+
TJ).

~
!
8 ERROR: ITS SOURCES, PROPAGATION, AND ANALYSIS
Proof
First note the meaning of the derivative notation in (1.1.12).
As
an
example
The
subscript notation, x = x
0
,
y = y
0
,
means the various derivatives
are to be-evaluated at
(x
0
,
y
0
).
The
proof
of (1.1.12)
is
based on applying the earlier Taylor's theorem
to
F(t) =
f(xo
+
t~,
Yo+ !1J)
O~t~1
Using Theorem 1.4,
F'(O)
F<n>(o)
F<n+I>(o)
F(1)
= F(O) +
ll
+ · · · + n! +
(n
+
1
)!
for some 0
~
8
~
1.
Clearly,
F(O)
=
f(x
0
,
y
0
),
F(1) =
f(x
0
+~.Yo+
1'/).
For
the first derivative,
aj(x
0
+
rt
Yo+
r.,.,)
aj(x
0
+
rt
Yo+
t'T/)
F'(t)
=
~
+
11------
ax
ay
=[~:X
+
1'/
:Y
]J(x,
y)lx-xo+t~
y-yo+I1J
The
higher order derivatives are calculated similarly.
•
Example As a simple example, consider expanding
f(x,
y)
=
xjy
about
(x
0
,
y
0
)
= (6, 2). Let n =
1.
Then
x aJ(6,2)
af(6,2)
y =
/(6,2)
+
(x-
6)
.
ax
+
(y-
2)-ay-
1[
2
a
2
/(a,r) a
2
J(a.
r)
+ 2
(x-
6)
. ax2 +
2(x-
6)(y-
2)-ax_a_y_
1 3
= 3 +
2(x
- 6) -
2(y
- 2)
+(y-2)2·
a2J(a,r)]
ayz
1 [ 2 1 2
28]
+
2"
(x
-
6)
· 0 - 2(x -
6)(y-
2)
12
+
(y
-
2)
·
yr

MATHEMATICAL PRELIMINARIES 9
with (o,
y)
a point
on
L(6,2; x,
y).
For
(x,
y)
close to (6,2),
X 1 3
-
~
3 +
-x-
-y
y 2 2
The graph
of
z = 3 +
}x-
}y
is
the plane tangent to the graph of z =
xjy
at
(x,
y,
z)
= (6,2,3).
Some mathematical notation There are several concepts that are taken up in
this text
that
are needed in a simpler form in the earlier chapters. These include
results on divided differences of functions, vector spaces, and vector and matrix
norms. The minimum necessary notation
is
introduced at this point, and a more
complete development
is
left to other more natural places in the text.
For
a given function
f(x),
define
(1.1.13)
assuming
x
0
,
x
1
,
x
2
are distinct. These are called the. first- and second-order
divided differences of
f(x),
respectively. They are related to derivatives of
f(x):
(1.1.14)
with
g between x
0
and x
1
,
and t between the minimum and maximum
of
x
0
,
x
1
,
and x
2
•
The
divided differences are independent
of
the order of their arguments,
contrary to what might be expected from (1.1.13). More precisely,
(1.1.15)
for any permutation
(i,
j,
k)
of (0,
1,
2).
The proofs of these and other properties
are left as problems. A complete development
of
divided differences
is
given in
Section 3.2
of
Chapter
3.
The subjects of vector spaces, matrices, and vector and matrix norms are
covered in Chapter
7,
immediately preceding the chapters on numerical linear
algebra. We introduce some
of
this material here, while leaving the proofs till
Chapter
7.
Two vector spaces are used in a great many applications. They are
C
[a,
b]
= {
/(
t)
1/(
t)
continuous and real valued, a
:s;
t
:s;
b}

10 ERROR: ITS SOURCES, PROPAGATION, AND ANALYSIS
For
x, y E
R"
and a a real number, define x + y and
ax
by
[
xl
~
Ytl
x+y=
:
X"+
Yn
ax=
[a~ll
ax"
For
f, g E
C[a,
b] and a a
real
number, define f + g and
af
by
(!
+
g)(
t) =
/(
t) + g( t)
(af)(t)
=
af(t)
a~t~b
Vector norms are used
to
measure the magnitude of a vector. For
R",
we
define initially two different norms:
For
C[a,
b], define
llxlloo
=
max
Jx;l
1
:s;
i :s;"
11/lloo
=
max
1/(t)l
a:5,t:s;b
X E
R"
(1.1.16)
X E
R"
(1.1.17)
/E
C[a,
b] (1.1.18)
These definitions can be shown
to
satisfy the following three characteristic
properties of
all norms.
1.
llvll
;e:
0;
llvll
= 0
if
and only
if
v =
0,
the zero vector
2.
JJaviJ
=
Jal
·llviJ,
for all vectors v and real numbers a
3. llv +
wJI
~
JlviJ
+
IJwiJ,
for
all vectors v and w
Property (3)
is
usually referred
to
as
the triangle inequality. An explanation of
this name and a further development of properties and norms for
C[a,
b]
is
given
in
Chapter
4.
Norms
ca11
also be introduced
for
matrices. For an n X n matrix
[""
al1
a,.
l
a21
a22
a2n
A=
.
anl
an2
a""
define
n
JIAIIoo
=
m~
I:
Jaijl
(1.1.19)
l:5.t:5.n
j-l
With this definition, the properties of a vector norm will be satisfied. In addition,

COMPUTER REPRESENTATION
OF
NUMBERS
11
it can be shown that
(1.1.20)
(1.1.21)
where A and B are arbitrary n X n matrices. The proofs of these results are left
to the problems. They are also taken up in greater generality in Chapter
7.
Exmnple Consider the vector space R
2
and matrices of order 2 X
2.
In particu-
lar, let
x=
nJ
Then
IIAIIoo
= 5
IIYIIoo
= 7
and
(1.1.21)
is
easily satisfied. To show that (1.1.21) cannot be improved upon,
take
x=
[n
y
=Ax=
[~]
Then
1.2 Computer Representation of Numbers
Digital computers are the principal means of calculation in numerical analysis,
and consequently it is very important to understand how they operate. In this
section
we
consider how numbers are represented in computers, and in the
remaining sections
we
consider some consequences of the computer representa-
tion of numbers and of computer arithmetic.
Most computers have an
integer mode and a floating-point mode for repre-
senting numbers. The integer mode is used only to represent integers, and it will
not
concern us any further. The floating-point form is used to represent real
numbers. The numbers allowed can be
of greatly varying size, but there are
limitations on both the magnitude of the number and on the number of digits.
The floating-point ·representation
is
closely related to what
is
called scientific
notation in many high school mathematics texts.
The number base used in computers is seldom decimal. Most digital com-
puters use the base 2 (binary) number system or some variant of it such
as
base 8
(octal)
or
base 16 (hexadecimal).

12
ERROR:
ITS
SOURCES, PROPAGATION, AND ANALYSIS
Example (a)
In
base
2,
the digits are 0 and
1.
As an example of the conversion
of
a base 2
number
to decimal,
we
have
(1101l.Olh
= 1 · 2
4
+ 1 · 2
3
+ 0 · 2
2
+ 1 · 2
1
+ 1 · 2° +
0.
2-
1
+
1.
2-
2
= 27.25
When
using numbers in some other base, we will often use
(x)p
to indicate that
the
number
x is to
be
interpreted in the base
{3
number system.
(b)
In
base 16, the digits are
0,
1,
...
,
9,
A,·-··,
F.
As an example of the
conversion
of
such a number to decimal, we have
(56C.F)
16
= 5 · 16
2
+ 6 · 16
1
+ 12 · 16° +
15
·
16-
1
= 1388.9375
The
conversion
of
decimal numbers to binary
is
examined in the problems.
Let
{3
denote the number base being used in the computer. Then a nonzero
number
x in the computer is stored essentially in the form
(1.2.1)
with
o = + 1
or
- 1, 0
.:::;
a;
.:::;
{3
-
1,
e an integer, and
The
term o is called the sign, e is called the exponent, and
(.a
1
· • • a
1
)p
is called
the
mantissa
of
the floating-point number x. The number
{3
is also called the
radix, and the point preceding a
1
in (1.2.1) is called the radix point, for example,
decimal
point
(/3
= 10), binary point
(/3
=
2).
The
integer t gives the number of
base
{3
digits in the representation.
We
will always assume
giving
what
is called the normalized floating-point representation, We will also
assume
that
{1.2.2)
which limits the possible size
of
x.
The
number x = 0
is
always allowed,
requiring a special representation. Table 1.1 contains the values
of
{3,
t,
L,
and U
for a
number
of
common computers.
The
use.
of
{3,
t,
L,
and U to specify the
arithmetic characteristics is based
on
that in [Forsythe
et
al. (1977), p. 11]. Some
computers use a different placement of the radix point (e.g.,
CDC
CYBER). We
have modified their exponent bounds so that the limits
on
the size of a
floating-point number will be correct when using the theory
of
this section. We
also include results for double precision representations
on
some computers that
include
it
in
their hardware. In
Table
1.1 there are additional columns that will
be
explained later.
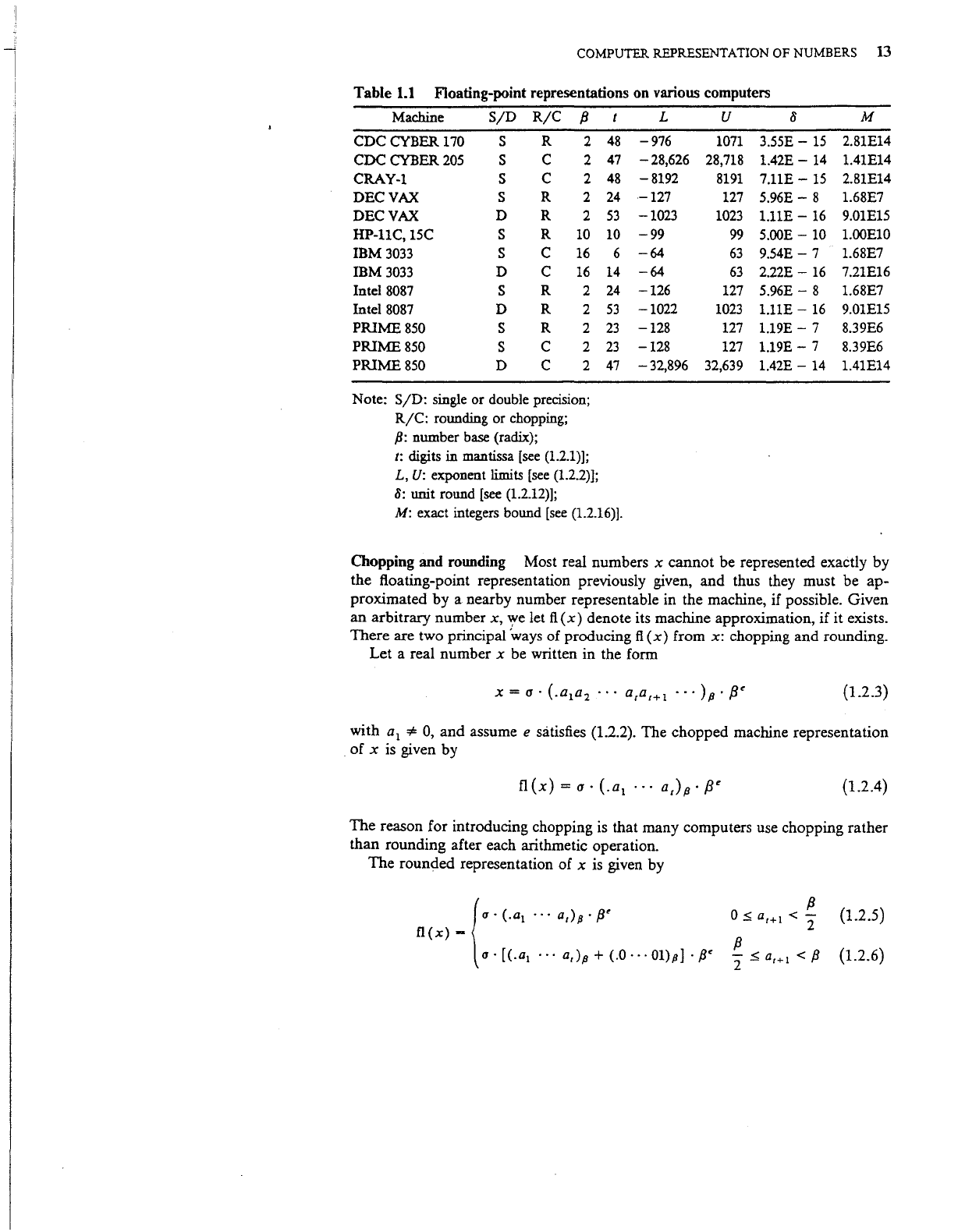
COMPUTER REPRESENTATION OF NUMBERS
13
Table
1.1
Floating-point representations on various computers
Machine
S/D
R/C
fJ
t
L
u 8
M
CDC CYBER
170
s
R
2
48
-976
1071
3.55E-
15
2.81E14
CDC CYBER
205
s
c 2
47
-28,626
28,718
1.42E-
14
1.41E14
CRAY-1
s
c 2
48
-8192
8191
7.11E-
15
2.81E14
DEC
VAX
s
R 2
24
-127
127
5.96E-
8
1.68E7
DEC
VAX
D R 2
53
-1023
1023
l.llE-
16
9.01E15
HP-UC,
15C
s R
10 10
-99
99
5.00E-
10
LOOE10
IBM
3033
s c
16
6
-64
63
9.54E-
7
1.68E7
IBM
3033
D c
16 14
-64
63
2.22E-
16
7.21E16
Intel8087
s
R
2
24
-126
127
5.96E-
8
1.68E7
Intel8087 D R 2
53
-1022
1023
1.11E-
16
9.01E15
PRIME850
s
R 2
23
-128
127
1.19E-
7
8.39E6
PRIME850
s
c 2
23
-128
127
1.19E-
7
8.39E6
PRIME850 D c 2
47
-32,896
32,639
1.42E-
14
1.41E14
Note:
SjD:
single or double precision;
R/C:
rounding or chopping;
{J:
number
base
(radix);
t: digits in mantissa
[see
(1.2.1)];
L,
U:
exponent limits
[see
(1.2.2)];
8:
unit round
[see
(1.2.12)];
M:
exact integers bound
[see
(1.2.16)].
Chopping and rounding Most real numbers x
cannot
be
represented exactly
by
the
floating-point representation previously given,
and
thus they must
be
ap-
proximated
by
a nearby number representable in the machine, if possible. Given
an
arbitrary
number
x,
'Ye
let fl (
x)
denote its machine approximation,
if
it exists.
There
are two principal 'ways of producing fl
(x)
from
x:
chopping
and
rounding.
Let
a real
number
x be written in the form
{1.2.3)
with a
1
=I=
0,
and
assume e satisfies (1.2.2).
The
chopped
machine representation
of
x is given by
(1.2.4)
The
reason for introducing chopping is that many computers use chopping
rather
than
rounding after each arithmetic operation.
The
rounded representation of x is given by
· · ·
a,)p
+ (.0 · · · 01)p] · W
{
u·(.a
1
II(x)-
u·[(.al
···
a,)p
· W
fJ
O.sa,+J<2
fJ
2
.S
a,+J
<
fJ
(1.2.5)
{1.2.6)
