Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


I
l
!
14 ERROR: ITS SOURCES, PROPAGATION, AND ANALYSIS
In the last fonnula, (.0·· · · Ol)p denotes /3-
1
•
Although this definition of
fl(x)
is somewhat fonnal,
it
yields the standard definition of rounding that most
people have learned for decimal numbers. A variation of this definition
is
sometimes used in order
to
have unbiased rounding. In such a case, if
f3
(1)
at+I = 2
and
(2)
aj
= 0 for j
~
t + 2
then whether to round up or down
is
based on whether a
1
is
odd or even,
respectively. This-leads.to the unbiased rounding rule that most people learn for
rounding decimal-numbers; but-we-will-henceforth assume the simpler definition
(1.2.5)-(1.2.6).
With most real numbers
x,
we
have fl
(x)
*
x.
Looking at the relative (or
percentage) error, it can be shown that
x-fl(x)
(1.2.7)
-{
X
with
- /3-t+l
:5:
{
:5:
0
chopped
fl
(
x)
(1.2.8)
_lf3-t+I
< { < lf3-t+I
2 - - 2
rounded
fl
(
x)
(1.2.9)
We will show the result (1.2.8) for chopping; the result (1.2.9) for rounding
is
left
as a problem.
Assume
a = + 1, since the case a =
-1
will not change the sign of
E:.
From
(1.2.3) and (1.2.4),
we
have
Letting
y =
f3
-
1,
x -
fl
(
x)
= ( .00 · · ·
Oat+
1
• • • ) p • W
o
:5:
x-
fl(x)
:5:
(.oo
· · ·
Oyy
· · ·
)p·
W
=
y(/3-1-1
+ {3-t-2 +
...
] .
f3"
This proves (1.2.8), and the proof of (1.2.9)
is
similar.

l
i
COMPUTER REPRESENTATION OF NUMBERS
15
The formula (1.2.7)
is
usually written in the equivalent form
fl(x)=(1+£)x
(1.2.10)
with
£ given by (1.2.8) or (1.2.9). Thus fi
(x)
can be considered to be a small
relative perturbation of x. This formula for
fi (
x)
also allows us to deal precisely
with the effects
of
rounding/chopping errors in computer arithmetic operations.
Examples
of
this are given
in
later sections. The definition of fi (
x)
and the
use
of
(1.2.10)
is
due to [Wilkinson
(1963)],
and
it
is
widely used in analyzing the effects
of rounding errors.
Accuracy of Ooating-point representation
We
now introduce two measures that
give a fairly precise idea of the possible accuracy
in
a floating-point representa-
tion. The first of these
is
closely related to the preceding error result (1.2.7)-(1.2.9)
for fl(x).
The
unit round of a computer
is
the number 8 satisfying:· (1) it
is
a positive
floating-point number, and
(2)
it
is
the smallest such number for which
fl(1+8)>1
(1.2.11)
Thus for any floating-point number
& <
8,
we
have fi
(1
+
8)
=
1,
and 1 + & and
1 are identical within the computer's arithmetic. This gives a precise measure of
how many digits of accuracy are possible in the representation of a number. Most
high-quality portable computer programs
use
the unit round in order to note the
maximal accuracy that
is
possible on the computer being used.
The unit round
8
is
easily calculated, and it is given by
chopped definition
of
fl
( x)
rounded definition of
fl
(
x)
(1.2.12)
We show this for rounded arithmetic on a binary machine. First
we
must show
Write
1 +
2-l
= [{.10
...
)2
+ (.00
...
010
...
h]2
1
i
position t + 1
= (.10
...
010
...
)2. 2
1
(1.2.13)
(1.2.14)
Form fl(1 +
2-
1
),
and note that there
is
a 1 in position t +
1,
of the mantissa.
Then from (1.2.6)
fl
(1
+
2-')
= {.10 · · ·
01h,
2
1
= 1 +
2-
1
+
1
i
position t

16 ERROR: ITS SOURCES, PROPAGATION, AND ANALYSIS
Thus
(1.2.13) is satisfied, although
The
fact
that
8
cannot
be smaller than 2
_,
follows easily
by
reexamining (1.2.14).
If
8 <
8,
then 1 + § has a 0 in position t + 1
of
the mantissa in (1.2.14):
and
the
definition (1.2.5)
of
rounding would
then
imply
fl.
(1 +
6)
=
1.
A second measure
of
the maximal accuracy possible in a floating-point
representation
is
to
find the largest integer M for which
man integer
and
0
~
m
~
M-
fl
(m) = m
(1.2.15)
This
also implies
ft(M
+ 1) * M + 1.
It
is
left as a problem to show that
M =
/3'
(1.2.16}
The
numbers
M and 8 for various computers are given in Table 1.1, along with
whether
the
computers round
(R)
or
chop (C). ·
Example
For
PRIME
computers in single precision,
M
= 2
23
= 8388608.
Thus
all integers with six decimal digits and most with seven decimal digits
can
be
st~red
exactly in the single precision floating-point representation. FGr the
unit
round,
8 =
2-zz,;,
2.38 x
w-
7
chopped arithmetic
s =
rzJ
,;,
1.19
x
w-7
rounded arithmetic
Users
of
the
PRIME
have
both
chopped
and
rounded arithmetic available to
them,
for
single .precision arithmetic.
In
almost
all cases, rounded arithmetic
is
greatly preferable
to
chopped
arithmetic.
This
is
examined
in
more detail in
later
sections,
but
the
main
reason
lies in
the
biased sign
of
£
in
(1.2.8) as compared to the lack
of
such bias in
(1.2.9).
Underflow and overflow When the exponent bounds
of
(1.2.2) are violated, then
the
associated
number
x of (1.2.1)
cannot
be represented
in
the computer. We
now
look
at
what
this says
about
the possible range in magnitude
of
x.
The
smallest positive floating-point.
number
is ·
Using
y =
f3
- 1, the largest positive floating-point number is
xu= (.y
...
y)p.
pu
=
(1-
p-').
pu

DEFINITIONS AND SOURCES
OF
ERROR 17
Thus
all floating-point numbers x must satisfy
(1.2.17)
Within
the
Fortran
language
of
most computers,
if
an arithmetic operation leads
to
a result x for which
lxl
>xu,
then this
will
be
a fatal error and the program
will terminate. This is called an
overflow error.
In
contrast, if
then usually
ft
(x)
will be set to zero
and
computation will continue. This
is
called
an
underflow error.
Example Consider evaluating x = s
10
on an
IBM
mainframe computer. Then
there will
be
an
underflow error if
Thus
x = s
10
will be set to zero if
lsi
<
1.49
X
10-
8
.
Also, there will be
an
overflow
error
if
or
equivalently,
lsi
> 3.9 X 10
7
1.3 Definitions
and
Sources of
Error
We now give a rough classification of the major ways in which error is introduced
into
the solution
of
a problem, including some
that
fall outside the usual scope
of
mathematics.
We
begin with a few simple definitions
about
error.
In
solving a problem,
we
seek
an
exact or
true
solution, which we denote
by
Xr-
Approximations are usually made in solving the problem, resulting in
an
approximate
solution
xA.
We define the error in
xA
by
For
many
purposes, we prefer to study the percentage
or
relative error in xA,
XT-
XA
Rei
( x
A)
= relative error in x A =
---
xT
provided
xT
if=
0. This has already been referred to in (1.2.7), in measuring the
error
in
ft(x).
Example
xT
= e =
2.7182818
...
XA
=
¥=
2.7142857
...
Error
( x
A)
= .003996
...
Rei
(xA)
= .00147
...

J
18 ERROR: ITS SOURCES, PROPAGATION, AND ANALYSIS
In place of relative error,
we
often use the concept of significant digits.
We
say
xA has m significant (decimal) digits with respect to
Xr
if the error
Xr-
xA has
magnitude less than or equal to 5 in the (m
+ 1)st digit of
Xr,
counting to the
right from the first nonzero digit in
Xr·
Example (a)
XA
= .333
Since the error
is
less
than 5 in the fourth digit to the right of the first nonzero
digit in
Xr,
we say that xA has three significant digits with respect
to
xr.
(b)
Xr
= 23:496
XA
= 23.494
The
term xA has four significant digits with respect to
Xr,
since the error
is
less
than 5 in the fifth place to the right of the first nonzero digit in
Xr·
Note that if
x A is rounded to four places, an additional error
is
introduced and x A will no
longer have four significant digits.
· (c)
Xr
= .02138
XA
= .02144
lxr-
xA
I = .00006
The
number
xA
has
two
significant digits, but not three, with respect
to
xr.
The following
is
sometimes used in measuring significant digits.
If
l
xr-
xA I
Xr
.:=:;;
5 x
lo-m-1
(1.3.1)
then
xA has m· significant digits with respect
to
xr.
To show this, consider the
case
.1
.:=:;;
lxrl
<
1.
Then (1.3.1) implies
Since
.1
.:=:;;
Xr
<
1,
this implies xA has m significant digits. The proof for a
general
Xr
is essentially the same, using
Xr
=
Xr
·
lOe,
with
.1
.:=:;;
lxrl
<
1,
e an
integer.
Note
that (1.3.1)
is
a sufficient condition, but not a necessary condition,
in order that
xA
have m significant digits. Examples (a) and (b) just given have
one
more significant digit than that indicated by the test (1.3.1).
Sources of error
We
now
give
a rough classification of the major sources of
error
..
(Sl)
Mathematical modeling of a physical problem A mathematical model
for a physical situation is an attempt to
give
mathematical relationships between
certain quantities of physical interest. Because of the complexity of physical
reality, a variety of simplifying assumptions are
usetl
to
construct a more
tractable mathematical model. The resulting model has limitations on its accu-
racy as a consequence of these assumptions, and these
lirriitations may or may
not
be troublesome, depending on the uses of the model. In the case that the

DEFINITIONS AND SOURCES OF ERROR
19
model
is
not sufficiently accurate, the numerical solution of the model cannot
improve upon this basic lack of accuracy.
Example Consider a projectile
of
mass m to have been fired into the air, its
flight path always remaining close to the earth's surface. Let an
xyz coordinate
system be introduced with origin on the earth's surface and with the positive
z-axis perpendicular to the earth and directed upward. Let the position
of
the
projectile
at
time t be denoted by
r(t)
=
x(t)i
+
y(t)j
+ z(t)k, using the stan-
dard
vector field theory notation. One model for the flight of the projectile
is
given by Newton's second law
as
d
2
r{t)
dr(t)
m--
=
-mgk-
b--
dt2 dt
{1.3.2)
where b > 0
is
a constant and g
is
the acceleration due to gravity. This equation
says that the only forces acting on the projectile are (1) the gravitational force of
the earth, and (2) a frictional force that
is
directly proportional to the speed
lv(t)l =
ldr(t)jdti
and directed opposite to the
path
of flight.
In some situations this
is
an excellent model,
and
it may -not be necessary to
include even the frictional term. But the model doesn't include forces of resis-
tance acting perpendicular
to
the plane of flight, for example, a cross-wind, and it
doesn't allow for the
C<:>riolis
effect. Also, the frictional force in (1.29) may be
proportional to lv(t)la with a
-=F
1.
If
a model
is
adequate for physical purposes, then
we
wish to use a numerical
scheme that willpreserve this accuracy. But if the
model
is
inadequate, then the
numerical analysis cannot improve the accuracy except by chance. On the other
hand,
it
is
not a good idea to create a model that
is
more complicated than
needed, introducing terms that are relatively insignificant with respect to the
phenomenon being studied. A more complicated model can often introduce
additional numerical analysis difficulties, without yielding any significantly greater
accuracy.
For
books concerned explicitly with mathematical modeling in the
sciences, see Bender (1978), Lin and Segal (1974), Maki and Thompson (1973),
Rubinow (1975).
(S2) Blunders In precomputer times, chance arithmetic errors were always a
serious problem. Check schemes, some quite elaborate, were devised to detect if
such errors had occurred and to correct for them before the calculations had
proceeded very far past the error.
For
an example, see Fadeeva (1959) for check
schemes used when solving systems of linear equations.
With the introduction of digital computers, the type
of
blunder has changed.
Chance arithmetic errors (e.g., computer malfunctioning) are now relatively rare,
and programming errors are currently the main difficulty.
Often a program error
will be repeated many times in the course
of
executing the program, and its
existence becomes obvious because of absurd numerical output (although the
source of the error may still be difficult to find). But as computer programs
become more complex and lengthy, the existence of a small program error may
be hard to detect and correct, even though the error may make a subtle, but

20 ERROR: ITS SOURCES, PROPAGATION, AND ANALYSIS
crucial difference in the numerical results. This makes good program debugging
very important, even though it may not seem very rewarding immediately.
To
detect programming errors, it
is
important to have some way of checking
the accuracy of the program output. When first running the program, you should
use cases for which you know the correct answer, if possible. With a complex
program, break it into smaller subprograms, each of which can be tested
separately. When the entire program has been checked out and you believe it
to
be correct, maintain a watchful eye
as
to whether the output
is
reasonable or not.
(83) Uncertainty in physical data Most data from a physical experiment
will
contain error
or
uncertainty within it. This must affect the accuracy of any
calculations based on the data, limiting the accuracy of the answers. The
techniques for analyzing the effects in other calculations of this error are much
the same as those used in analyzing the effects of rounding error, although the
error in data is usually much larger than rounding errors. The material of the
next sections discusses this further.
(84) Machine errors
By
machine errors
we
mean the errors inherent in using
the floating-point representation of numbers. Specifically,
we
mean the round-
ing/
chopping errors and the underflow 1 overflow errors. The.
rounding/
chopping
errors are due to the finite length of the floating-point mantissa; and these errors
· occur with all
of
the computer arithmetic operations. All of these forms of
machine error were discussed in Section 1.2; in the following sections,
we
consider some
of
their consequences. Also, for notational simplicity,
we
hence-
forth let the term
rounding
error
include chopping where applicable.
(85) Mathematical truncation error This name refers
to
the error of ap-
proximation in numerically solving a mathematical problem, and it
is
the error
generally associated with the subject of numerical analysis.
It
involves the
approximation
of
infinite processes by finite ones, replacing noncomputable
problems with computable ones.
We
use some examples to make the idea more
precise.
Example (a) Using the first two terms of the Taylor series from (1.1.7),
.ff+X
= 1 +
tx
(1.3.3)
which is a good approximation when x
is
small.
See
Chapter 4 for the general
area of approximation of functions.
(b)
For
evaluating an integral on
[0,
1],
use
ft(x)
dx =
!._
E
t(-
21
~·
2
---
1
)
o n
j-l
n
n=1,2,3,
...
(1.3.4)
This is called the
midpoint numerical integration
rule:
see the last part of Section
5.2 for more detail. The general topic of numerical integration is examined in
Chapter
5.

DEFINITIONS AND SOURCES
OF
ERROR
21
(c)
For
the differential equation problem
Y'(t) =
f(t,
Y(t))
(1.3.5)
use the approximation of the derivative
Y(
t + h) -
Y(
t)
Y'(
t)
~
___
____;_~
h
for some small
h.
Let
ti
= t
0
+
jh
for j
~
0,
and define an approximate solution
function
y(tj)
by
Thus
we
have
This
is
Euler's
method for
solving_
an initial value problem for an ordinary
differential equation. An-extensive'discussion and analysis of it is-given in Section
6.2. Chapter 6 gives a complete development
of
numerical methods for solving
the initial value problem
(1.3.5). -
Most numerical analysis problems in the following chapters involve mainly
mathematical truncation errors. The major exception
is
the solution of systems of
linear equations
in which rounding errors are often the major source of error.
Noise
in
function evaluation One of the immediate consequences of rounding
errors is that the evaluation of a function
f(x)
using a computer will lead to an
approximate function
/(x)
that
is
not continuous, although it
is
apparent only
when the graph of
/(x)
is
looked at on a sufficiently small scale. After each
arithmetic operation that
is
used in evaluating
f(x),
there will usually be a
rounding error. When the effect of these rounding errors
is
considered,
we
obtain
a computed value
/(x)
whose error
f(x)-
/(x)
appears
to
be a small random
number as
x varies. This error in
/(x)
is
called noise. When the graph of
/(x)
is
looked
at
on
a small enough scale, it appears
as
a fuzzy band of dots, where the x
values range over
all
acceptable floating-point numbers on the machine. This has
consequences for many other programs that make use of
/<x). For example,
calculating the root of
J(x)
by using /<x)
will
lead
to
uncertainty in the location
of
the root, because it will likely be located in the intersection of the x-axis and
the fuzzy banded graph of
/<x). The following example shows that this can result
in considerable uncertainty in the location of the root.
Example
Let
f(x)
= x
3
-
3x
1
+
3x-
1
(1.3.6)
which is
just
(x
- 1)
3
•
We
evaluated (1.3.6) in the single precision BASIC of a
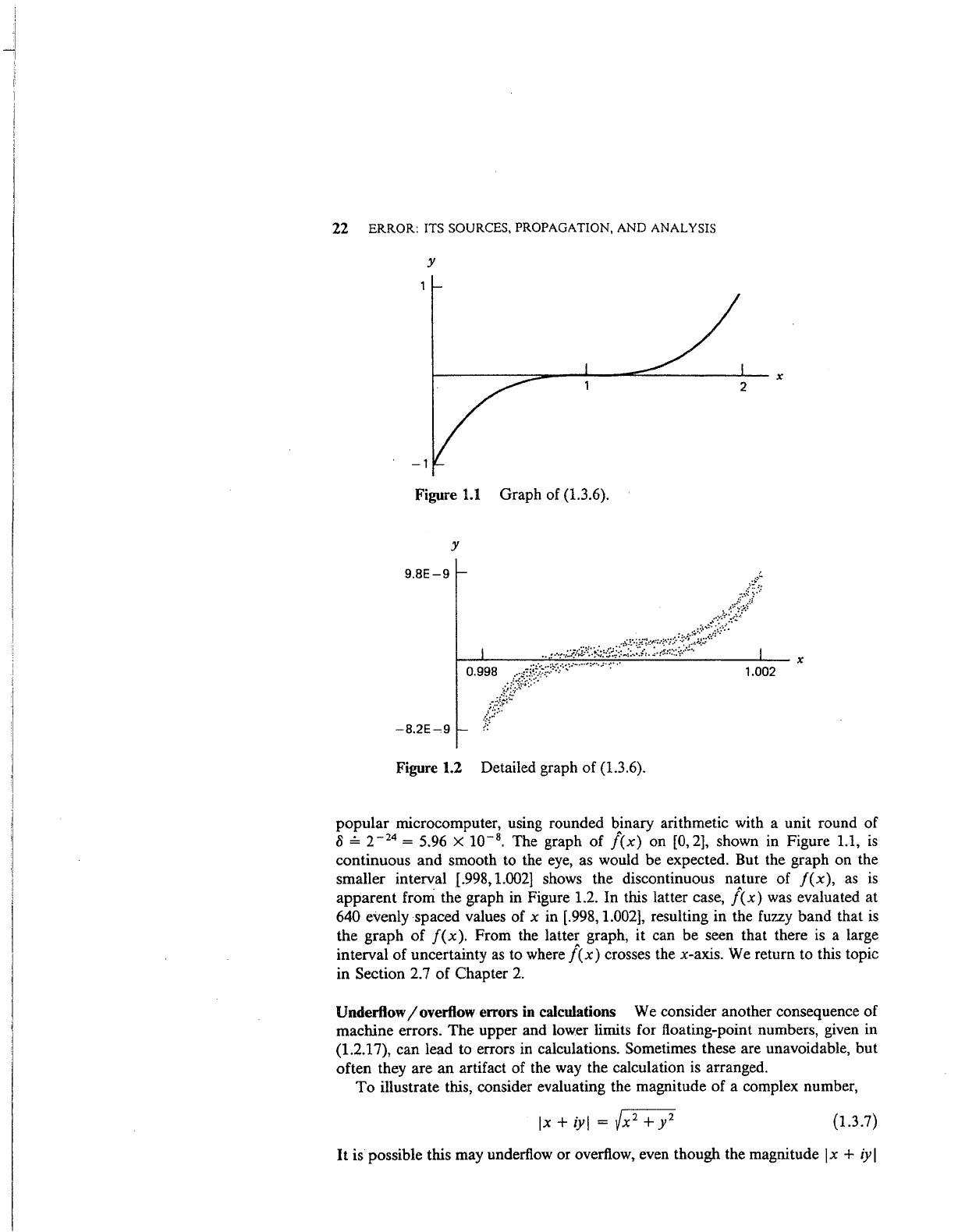
22 ERROR: ITS SOURCES, PROPAGATION, AND ANALYSIS
y
-1
Figure
1.1
Graph of (1.3.6).
y
9.8E-9
Figure 1.2 Detailed graph
of
(1.3.6).
popular
microcomputer, using rounded binary arithmetic with a unit round
of
8
~
r
24
= 5.96 X
10-
8
•
The graph
of
/(x)
on
[0,
2],
shown in Figure 1.1,
is
continuous
and
smooth to the eye, as would
be
expected. But the graph on the
smaller interval [.998,
1.002] shows the discontinuous nature
of
f(x),
as
is
apparent
from the graph in Figure 1.2.
In
this latter case,
/(x)
was evaluated at
640 evenly spaced values
of
x in [.998, 1.002], resulting in the
fu7..zy
band
that is
the
graph
of
f(x).
From the latter graph, it can
be
seen that there is a large
interval
of
uncertainty as to where
/(x)
crosses the x-axis. We return to this topic
in Section
2.7
of
Chapter
2.
Underflow I overflow errors in calculations We consider another consequence
of
machine errors.
The
upper and lower limits for floating-point numbers, given in
(1.2.17),
can
lead to errors in calculations. Sometimes these are unavoidable,
but
often they
are
an
artifact of the way the calculation is arranged.
To
illustrate this, consider evaluating the magnitude
of
a complex number,
(1.3.7)
It
is
possible this may underflow or overflow, even though the magnitude jx + iyl

PROPAGATION OF ERRORS
23
is
within machine limits. For example, if
xu=
1.7 X
10
38
from (1.2.17), then
(1.3.7) will overflow for
x = y =
10
20
,
even
though jx + iyj =
1.4
X
10
20
•
To
avoid this, determine the larger of
x and y, say x. Then rewrite (1.3.7)
as
lx
+ iyl =
lxl
·
~
y
a=-
X
(1.3.8)
We must calculate
·./1
+ a
2
,
with 0
.:$;
a.:$;
1.
This avoids the problems of (1.3.7),
both
for underflow and overflow.
1.4 Propagation of
Errors
In this and the next sections,
we
consider the effect of calculations with numbers
that
are in error. To begin, consider the basic arithmetic operations. Let w denote
one of the arithmetic operations
+,
-,
X,
j;
and let w be the computer version
of
the same operation, which will usually include rounding. Let
xA
and
YA
be the
numbers being used for calculations, and suppose they are
in
error, with true
values
Then
xAwyA
is
the number actually computed,
and
for its error,
XrWYr-
xAwyA
=
[xrWYr-
xAwyA]
+
[xAWYA
- xAwyA]
(1.4.1)
The first quantity in brackets
is
called the propagated error, and the second
quantity
is
normally rounding or chopping error. For this second quantity,
we
usually have
(1.4.2)
which means that
xAwyA
is
computed exactly
and
then rounded. Combining
(1.2.9) and (1.4.2),
(1.4.3)
provided true rounding is used.
For
the propagated error,
we
examine particular cases.
Case (a) Multiplication. For the error
in
xAyA,
