Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


24 ERROR: ITS SOURCES, PROPAGATION, AND ANALYSIS
(1.4.4)
The symbol
"«
" means "much less than."
Case (b) Division.
By
a similar argument,
(1.4.5)
(1.4.6)
For
both multiplication and division, relative errors do not propagate rapidly.
Case
(c)
Addition and subtraction.
(1.4.7)
This appears quite good and reasonable, but it cim be misleading. The relative
error in
xA
±
YA
can be quite poor when compared with
Rei
(xA) and Rei
(YA).
Example Let Xr =
'TT,
xA
= 3.1416,
Yr
= lf,
YA
= 3.1429. Then
Xr-
XA
=
-7.35
X
10-
6
Rel (xA) =
-2.34
X
10-
6
Yr-
YA
=
-4.29
X
10-
5
(xr-
Yr)-
(xA-
YA)
=
-.0012645-
(-
.0013) =
:1.55
X
10-
5
Although the error in
xA
-
YA
is quite small, the relative error in
xA
-
YA
is
much larger than that in
xA
or
YA
alone.
Loss of significance errors This last example shows that
it
is
possible to have a
large decrease
in
accuracy, in a relative error sense, when subtracting nearly equal
quantities. This can be a very important way
in
which accuracy is lost when error
is propagated in a calculation. We now give some examples of this phenomenon,
along with suggestions
on
how
it may be avoided in some cases.

PROPAGATION OF ERRORS 25
Example Consider solving ax
1
+ bx + c = 0 when 4ac
is
small compared
to
b
2
;
use the standard quadratic formula for the roots
-b
+
Vb
2
-
4ac
r<I>
=
------
T
2a
-b-
Vb
2
-
4ac
rf>=
------------
2a
For
definiteness, consider x
2
-
26x + 1 =
0.
The formulas (1.4.8) yield
(1.4.8)
(1.4.9)
Now
imagine using a five-digit decimal machine. On it, /168
,;,
12.961. Then
define
rj
1
> =
13
+ 12.961 = 25.961
rj2>
=
13-
12.961 = .039 (1.4.10)
Using the exact answers,
Rei
(rJl>)
,;,
1.85 X
10-
5
(1.4.11)
Eor the -data entering into the calculation (1.4.10), using the notation of (1.4.7),
Jr=
/168
YA
= 12.961
Rei (yA)
,;,
3.71 x
10-
5
The
accuracy in
rj
2
>
is
much
less
than that of the data
xA
and
YA
entering into
the calculation. We say that significant digits have been lost in the subtraction
rj
2
> =
xA
-
yA,
or
that
we
have had a loss-of-significance
error
in calculating
rjl>.
In
rj
1
>,
we have
five
significant digits of accuracy, whereas
we
have only two
significant digits in
r,f>.
To
cure this particular problem, of accurately calculating
r,.f>,
convert (1.4.9)
to
Then use
13
-
v'168
rf>=
----
1
13
+
1168
13
+ /168
1 1
1
13 +
v'168
-----==
,;,
--
,;,
.038519 =
r<
2
>
13
+
v'168
25.961 . A
(1.4.12)
There are two errors here, that of
v'168
,;,
12.961 and that of the final division.
But each
of
these will have small relative errors [see (1.4.6)], and the new value of
rjl>
will be more accurate than the preceding one.
By
exact calculations,
we
now
have
much better
thim in (1.4.11).

26
ERROR:
ITS SOURCES, PROPAGATION, AND ANALYSIS
This new computation of r,fl demonstrates then the loss-of-significance error
is due to the form of the calculation, not to errors
in
the data of the computation.
In
this example it was easy to find an alternative computation that eliminated the
loss-of-significance error, but this is not always possible. For a complete discus-
sion of the practical computation of roots of a quadratic polynomial, see
Forsythe (1969).
Example With many loss-of-significance calculations, Taylor polynomial ap-
proximations
can
be used
to
eliminate the difficulty. We illustrate this with the
evaluation
of
1
ex-
1
J(x)
= 1 ex
1
dt
=
--
0 X
x#-0
(1.4.13)
For
x = 0, f(O) = 1; and easily,
f(x)
is
continuous at x =
0.
To see that there is a loss-of-significance problem when x
is
small,
we
evaluate
f(x)
at
x = 1.4 X
10-
9
,
using a popular and well-designed ten-digit hand
calculator. The results are
ex = 1.000000001
ex-
1
w-
9
--
= = .714
X 1.4 X
10-
9
(1.4.14)
The right-hand sides give the calculator results, and the true answer, rounded to
10 places, is
f(x)
= 1.000000001
The
calculation (1.4.14) has had a cancellation of the leading nine digits of
accuracy
in
the operands in the numerator.
To avoid the loss-of-significance error, use a quadratic Taylor approximation
to
ex and then simplify
f(x):
x x
2
J(x)
= 1 + - +
-e(
2 6
With the preceding x = 1.4 X
10-
9
,
f(x)
= 1 + 7 X
10-
10
with an error of less than
10-
18
•
(1.4.15)
In
general, use (1.4.15) on some interval
[0,
8], picking 8
to
ensure the error in
X
f(x)
= 1 + -
2
PROPAGATION OF ERRORS
27
is sufficiently small.
Of
course, a higher degree "approximation to ex could be
used, allowing a yet larger value
of
o.
In
general, Taylor approximations are often useful in avoiding loss-of-signifi-
cance calculations. But in some cases, the loss-of-significance error
is
more subtle.
Example Consider calculating a sum
(1.4.16)
with positive
and
negative terms Xp each
of
which is
an
approximate value.
Furthermore, assume the sum
S is much smaller than the maximum magnitude
of
the
xj"
In
calculating such a sum
on
a computer, it is likely that a loss-of-sig-
nificance
error
will occur. We give an illustration
of
this.
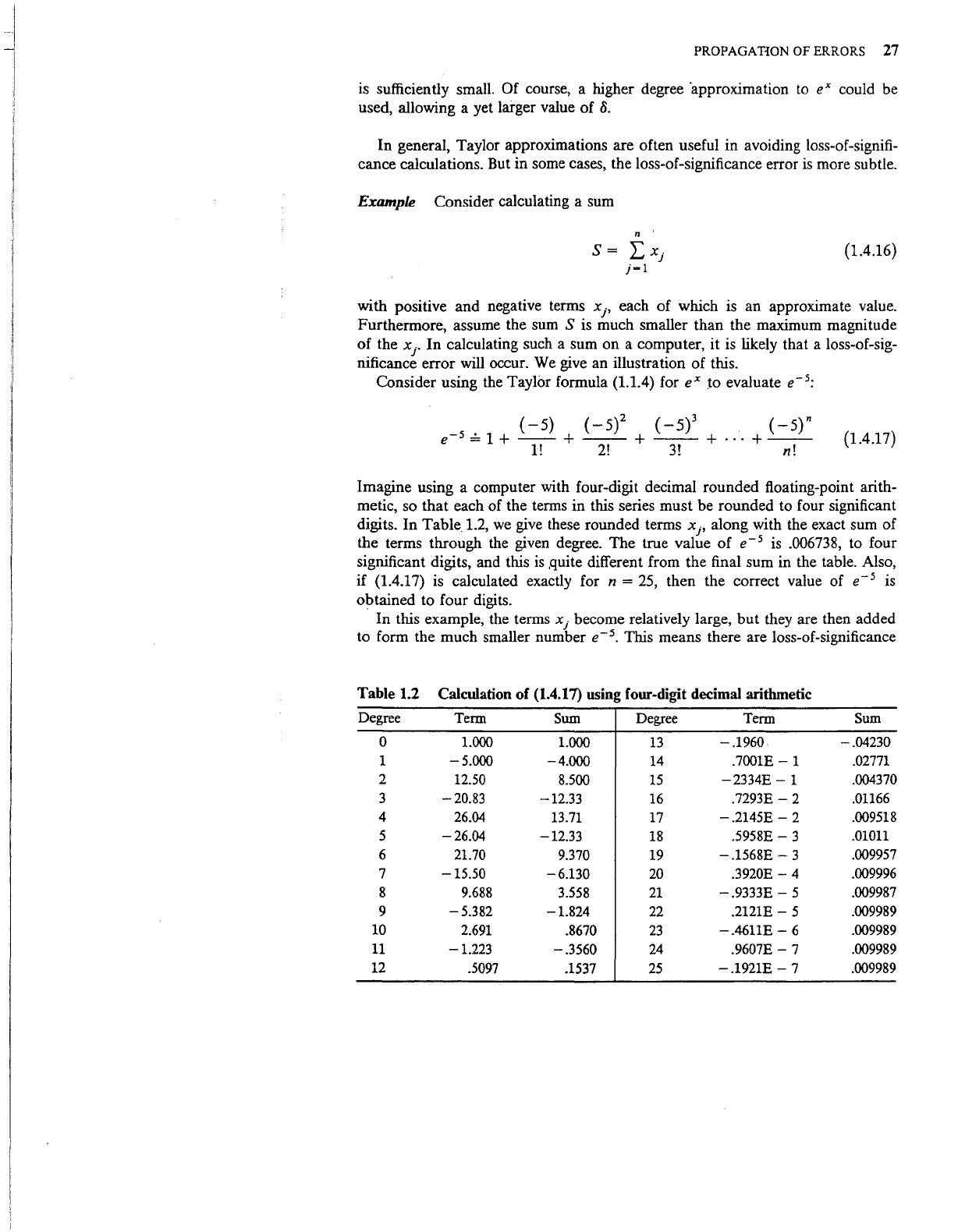
Consider using the Taylor formula (1.1.4) for
ex
to evaluate
e-
5
:
(
-5)
(
-5)
2
(
-5)
3
(
-sr
e-
5
~
1 +
--
+
--
+
--
+ · · · +
--
1!
2!
3!
n!
(1.4.17)
Imagine using a computer with four-digit decimal rounded floating-point
arith-
metic, so
that
each
of
the terms in this series
must
be rounded to four significant
digits.
In
Table
1.2,
we
give these rounded terms x
1
,
along with the exact sum
of
the terms through the given degree.
The
true value
of
e-
5
is
.006738, to four
significant digits, and this
is
.quite different from the final sum in the table. Also,
if (1.4.17) is calculated exactly for
n = 25, then the correct value of
e-
5
is
obtained to four digits.
In
this example, the terms
xj
become relatively large,
but
they are then added
to form the much smaller number
e-
5
•
This means there are loss-of-significance
Table 1.2
Calculation of (1.4.17) using four-digit decimal arithmetic
Degree
Term
Sum Degree Term Sum
0
1.000
1.000
13
-.1960
-.04230
1
-5.000 -4.000
14
.7001E-
1
.02771
2
12.50
8.500
15
-2334E-
1
.004370
3
-20.83
-12.33
16
.7293E-
2
.01166
4 26.04
13.71
17
-.2145E-
2 .009518
5
-26.04
-12.33
18
.5958E-
3
.01011
6 21.70
9.370
19
-.1568E-
3
.009957
7
-15.50
-6.130
20
.3920E-
4 .009996
8
9.688
3.558
21
-.9333E-
5 .009987
9
-5.382
-1.824
22
.2121E-
5 .009989
10
2.691
.8670
23
-.4611E-
6
.009989
11
-1.223
-.3560
24
.9607E-
7 .009989
12
.5097
.1537
25
-.1921E-
7
.009989

28 ERROR: ITS SOURCES, PROPAGATION, AND ANALYSIS
errors· in the calculation of the sum. To avoid this problem
in
this case
is
quite
easy. Either use
and form e
5
with a series not involving cancellation of positive and negative
terms;
or
simply form
e-
1
=
lje,
perhaps using a series, and
mu:jply
it times
itself to form
e-
5
•
With other series, it
is
likely that there
will
not be such a
simple solution.
Propagated error in function evaluations Let
f(x)
be a given function, and let
/(x)
denote the result of evaluating
f(x)
on a computer. Then
f(xr)
denotes the
desired function value and
/cxA)
is
the value actually computed. For the error,
we
write
(1.4.18)
The first quantity
in
brackets
is
called the propagated
error,
and the second
is
the
error due to evaluating
f(xA)
on a computer.
This
second error
is
generally a
small random number, based on an assortment of rounding errors that occurred
in carrying out the arithmetic operations defining
f(x).
We
referred to it earlier
in Section 1.3 as the noise in evaluating
f(x).
For
the propagated error, the mean value theorem
gives
(1.4.19)
This assumes that
xA
and Xr are relatively close and that
f'(x)
does not vary
greatly for
x between x A and Xr.
Example
sin('IT/5)-
sin(.628) = cos('1T/5)[('1T/5)-
.628]
= .00026, which
is
an excellent estimation of the error.
Using Taylor's theorem (1.1.12) for functions of two variables,
we
can gener-
alize the preceding
to
propagation of error in functions of two variables:
(1.4.20)
with
fx =
aj;ax.
We
are assuming that
fx(x,
y)
and
/y(x,
y)
do not vary greatly
for
(x,
y)
between
(xr,
Yr)
and (xA,
YA).
Example
For
f(x,
y)
= xY,
we
have fx =
yxrt,
/y =
xY
log(x). Then (1.4.20)
yields
(1.4.21)

ERRORS
IN
SUMMATION
29
The
relative error in
x~"
may be large, even though Rel(xA) and Rel(yA) are
small. As a further illustration, take
Yr =
YA
= 500,
xT
= 1.2, x A = 1.2001. Then
xfr
= 3.89604 X 10
39
,
x~"
= 4.06179 X 10
39
,
Rei
(x~")
= - .0425. Compare this
with Rel(xA)
=
8.3
X
w-s.
Error
in
data
If
the input
data
to an algorithm contain only r digits of
accuracy, then it is sometimes suggested that only r-digit arithmetic should be
used in any calculations involving these data. This is nonsense.
It
is certainly true
that
the limited accuracy of the data will affect the eventual results of the
algorithmic calculations, giving answers that are in error. Nonetheless, there
is
no
reason to make matters worse by using r-digit arithmetic with correspondingly
sized rounding errors. Instead one should use a higher precision arithmetic, to
avoid any further degradation in the accuracy
of
results of the algorithm. This
will lead to arithmetic rounding errors that are less significant than the error in
the data, helping to preserve the accuracy associated with the data.
1.5 Errors
in
Summation
Many
numerical methods, especially in linear algebra, involve sununations. In
this section, we look at various aspects
of
summation, particularly as carried out
in
floating-point arithmetic.
Consider the computation of the sum
m
with x
1
,
•••
, xm floating-point numbers. Define
s2 =
fl
(xl
+ x2) =
(xl
+
x2)(1
+ £2)
where we have made use of (1.4.2) and (1.2.10). Define recursively
r = 2,
...
,
m-
1
Then
(1.5 .1)
(1.5.2)
(1.5.3)
The
quantities
t:
2
,
•••
,
t:m
satisfy (1.2.8) or (1.2.9), depending on whether chop-
ping
or
rounding is used.
Expanding the first
few
sums,
we
obtain the following:
s2-
(xl
+ x2) = €2(xl +
x2)
S3-
(xl
+
X2
+ x3) =
(xl
+ x2)€2 +
(xi+
x2)(1
+ €2)€3 +
X3£3
=
(xl
+ x2)£2 +
(xl
+
X2
+ x3)t:3
S4-
(xl
+
X2
+
X3
+ x4) =
(xl
+ x2)t:2 +
(xi
+
X2
+ x3)t:3
+(xi+
x2 +
x3
+ x4)t:4
30 ERROR: ITS SOURCES, PROPAGATION, AND ANALYSIS
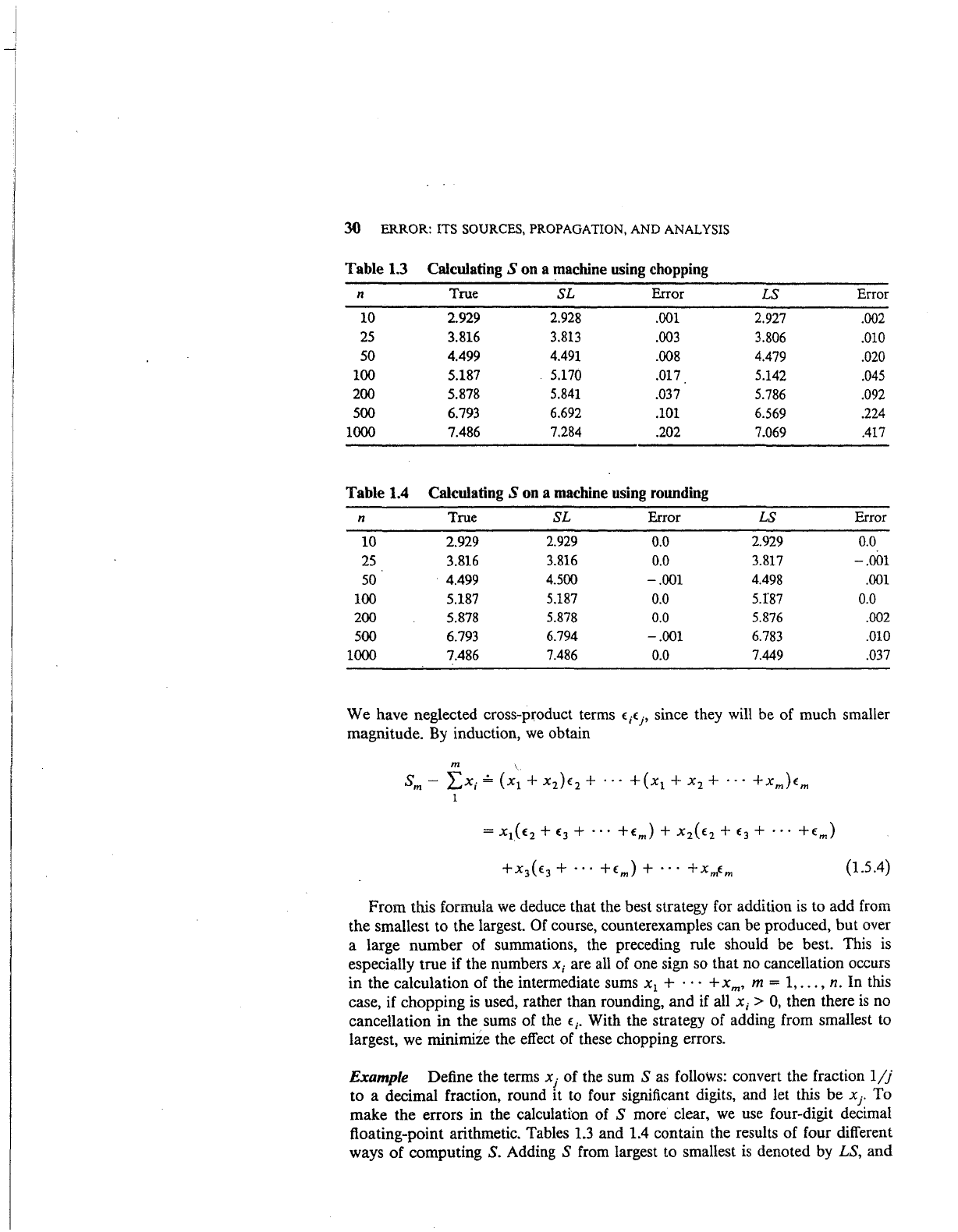
Table 1.3 Calculating S on a machine using chopping
n True
SL
Error
LS
Error
10 2.929 2.928 .001
2.927 .002
25
3.816 3.813
.003 3.806
.010
50
4.499 4.491 .008
4.479
.020
100
5.187 5.170 .017 5.142
.045
200
5.878 5.841
.037 5.786
.092
500
6.793
6.692
.101
6.569
.224
1000
7.486 7.284
.202 7.069 .417
Table 1.4 Calculating S on a machine using rounding
n
True
SL Error
LS
Error
10
2.929
2.929
0.0
2.929 0.0
25 3.816
3.816
0.0
3.817
-.001
50 4.499
4.500
-.001
4.498 .001
100
5.187
5.187
0.0
5.I87 0.0
200
5.878
5.878
0.0 5.876
.002
500
6.793
6.794
-.001
6.783 .010
1000 7.486
7.486
0.0
7.449
.037
We have neglected cross-product terms
€;€
1
,
since they
will
be of much smaller
magnitude.
By
induction,
we
obtain
m \
sm-
LX;=
(xl +
x2)€2
+
...
+(xl
+
x2
+
...
+xm)(m
1
(1.5.4)
From this formula
we
deduce that the best strategy for addition
is
to add from
the smallest to the largest.
Of course, counterexamples can be produced, but over
a large number of summations, the preceding rule should be best. This
is
especially true if the numbers
X;
are
all
of one sign
so
that no cancellation occurs
in the calculation of the intermediate sums x
1
+ · · · +xm, m =
1,
...
, n. In this
case, if chopping
is
used, rather than rounding, and if
all
x;
>
0,
then there
is
no
cancellation in the sums of the
€;.
With the strategy of adding from smallest
to
largest,
we
minimize the effect of these chopping errors.
Example Define the terms x
1
of the sum S
as
follows: convert the fraction
1/j
to a decimal fraction, round it
to
four significant digits, and let this be x
1
.
To
make the errors in the calculation of S more clear,
we
use
four-digit decimal
floating-point arithmetic. Tables
1.3
and 1.4 contain the results of four different
ways of computing S. Adding
S from largest to smallest
is
denoted by LS, and

ERRORS
IN SUMMATION
31
adding from smallest to largest
is
denoted by
SL.
Table
1.3
uses
chopped
arithmetic, with
(1.5 .5)
and Table 1.4 uses rounded arithmetic, with
-
.0005
.::::;
Ej
.::::;
.0005
(1.5.6)
The numbers
£.
1
refer to (1.5.4), and their bounds come from (1.2.8) and (1.2.9).
In
both tables, it
is
clear that the strategy of adding S from the smallest term
to the largest
is
superior to the summation from the largest term
to
the smallest.
Of much more significance, however,
is
the far smaller error with rounding as
compared to chopping. The difference
is
much more than the factor of 2 that
would come from the relative size of the bounds in
(1.5.5) and (1.5.6).
We
next
give an analysis of this.
A statistical analysis of error propagation Consider a general error sum
n
E = L
f.}
j=l
of the type that occurs in the summation error (1.5.4). A simple bound
is
lEI.::::;
nS
(1.5.7)
(1.5 .8)
where S is a bound on £
1
,
...
,
f.n.
Then S = .001 or
.0005
in
the preceding
example, depending on whether chopping or rounding
is
used. This bound (1.5.8)
is
for the worst possible case
in
which all the errors £
1
are as large
as
possible and
of the same sign.
-----When-using-rounding,-the
symmetry
in
sign behavior of the
£.
1
,
as shown in
(1.2.9), makes a major difference in the
size
of
E.
In
this case, a better model
is
to
assume that the errors
£
1
are uniformly distributed random variables in the
interval
[-
8,
8]
and that they are independent. Then
The sample mean
i
is
a new random variable, having a probability distribution
with mean
0 and variance S
1
j3n.
To calculate probabilities for statements
involving
i,
it
is
important to note that the probability distribution for i
is
well-approximated by the normal distribution with the same mean and variance,
even for small values such as
n
;;;:
10. This follows from the Central Limit
Theorem of probability theory [e.g., see Hogg and Craig (1978, chap.
5)].
Using
the approximating normal distribution, the probability
is
t that
lEI
.::::;
.39SVn

32 ERROR: ITS SOURCES, PROPAGATION, AND ANALYSIS
and
the probability
is
.99 that
lEI
~
1.498vn
(1.5.9)
The
result (1.5.9) is a considerable improvement upon (1.5.8) if n
is
at all large.
This analysis can also be applied to the case
of
chopping error. But in that
case,
-8
~
ei
~
0.
The
sample mean € now has a mean of
-oj2,
while
retaining the
same
variance
of
o
2
/3n.
Thus
there
is a probability of .99 that
(1.5.10)
For
large n, this ensures that E will approximately equal n8j2, which
is
much
larger
than
(1.5.9) for the case
of
rounding errors.
When these results,
(1.5.9) and (1.5.10), are applied to the general summation
error
(1.5.4), we see the likely reason for the significantly different error behavior
of
chopping
and
rounding in Tables 1.3 and 1.4.
In
general, rounded arithmetic
is
almost always
to
be preferred to chopped arithmetic.
Although statistical
analyses give more realistic bounds, they are usually much
more difficult
to
compute.
As
a more sophisticated example, see Henrici (1962,
pp.
41-59)
for a statistical analysis of the error in the numerical solution
of
differ~tial
equations. An example is given in Table 6.3 of Chapter 6 of the
present textbook.
Inner
products Given two vectors x,
Y.
E
Rm,
we
call
m
xTy = L
xjyj
j-1
(1.5.11)
the inner product of x and
y.
(The notation
xT
denotes the matrix transpose
of
x.)
Properties of the inner product are examined
in
Chapter
7,
but
we
note
here
that
(1.5.12)
(1.5.13)
The
latter inequality is called the Cauchy-Schwarz inequality, and it is proved in
a more general setting in Chapter
4.
Sums of the form (1.5.11) occur commonly
in
linear algebra problems (for example, matrix multiplication). We now consider
the numerical computation of such sums.
Assume
X;
and
Y;,
i = 1,
...
, m, are floating-point numbers. Define
k=l,2,
...
,m-1
(1.5.14)

ERRORS IN SUMMATION 33
Then as before, using
(1.2.10),
with the tenns f.j,
Tlj
satisfying (1.2.8) or (1.2.9), depending on whether chopping
or
rounding, respectively,
is
used. Combining and rearranging the preceding
formulas,
we
obtain
with
m
sm
=
L:
xjy/1-
'Yj)
j-1
~
1 + f.j +
Tlj
+
Tlj+l
+ · · ·
+11m
~
(1.5.15)
Til=
0
(1.5.16}
The
last approximation
is
based on ignoring the products of the small tenns
'll;'llk,f.;'llk· This brings
us
back to the same kind
of
analysis as was done earlier for
the sum (1.5.1). The statistical error analysis following (1.5.7) is also valid.
For
a
rigorous bound, it can be shown that if
m~
< .01, then
j = 1,
...
,
m,
(1.5.17)
where
~
is
the unit round given in (1.2.12) [see Forsythe and Moler (1967, p. 92)].
Applying this to (1.5.15) and using (1.5.13),
m
IS-
Sml
!5:
L IXjY/Yjl
j-1
(1.5.18)
This says nothing about the relative error, since
x
Ty
can be zero even though all
x;
and
Y;
are nonzero.
These results say that the absolute error in
Sm
~
XTJ
does not increase very
rapidly, especially if true rounding
is
used and we consider the earlier statistical
analysis
of
(1.5.7). Nonetheless,
it
is often possible to easily and inexpensively
reduce this error a great deal further, and this is usually very important
in
linear
algebra problems.
Calculate each product xjyj in a higher precision arithmetic, and carry out the
summation
in
this higher precision arithmetic. When the complete sum has been
computed, then round or chop the result back to the original arithmetic precision.
