Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


ROOTFINDING FOR NONLINEAR EQUATIONS 55
The
general iteration formula is then obtained by repeating the process, with x
1
replacing x
0
,
ad infinitum, to get
(2.0.4)
A form more convenient for theoretical purposes
is
obtained by introducing
the scaled residual
(2.0.5)
Using it,
n~O
(2.0.6)
For
the error,
1
'n
e
=--x
=-
" a n a
(2.0.7)
We will analyze the convergence
of
this method, its speed, and its dependence
on
x
0
•
First,
(2.0.8)
Inductively,
n~O
(2.0.9)
From
(2.0.7), the error
en
converges to zero as n
~
oo
if and only if
rn
converges
to zero.
From
(2.0.9), '"converges to zero if and only if
lrol
<
1,
or
equivalently,
-1
<
1-
ax
0
< 1
2
0 < x
0
<-
a
(2.0.10)
.
In
order
that
x" converge to
1/a,
it
is
necessary
and
sufficient that x
0
be
chosen
to satisfy (2.0.10).
To
examine the speed
of
convergence when (2.0.10) is satisfied, we obtain
formulas for the error and relative error. For the speed
of
convergence when
(2.0.10) is satisfied, ·
2 2 2
'n+l
'"
ena
e
=--=-=--
n+l
a a a
(2.0.11)
n~O
(2.0.12)

56 ROOTFINDING FOR NONLINEAR EQUATIONS
The
notation Rel
(x")
denotes the relative error in x". Based on equation (2.0.11),
we say
e" converges
to
zero tpUJdratically. To illustrate
how
rapidly the error will
decrease, suppose that
Rel(x
0
)
= 0.1. Then
Rel(x
4
)
=
10-
16
• Each iteration
doubles the number of
significant digits.
This example illustrates the construction of an iterative method for solving an
equation; a complete convergence analysis has been given. This analysis included
a proof of convergence, a determination of the
interval
of
convergence for the
choice of
x
0
,
and
a determination of the speed of convergence. These ideas are
examined
in
more detail in the following sections using more general approaches
to solving
(2.0.1).
Definition A sequence of iterates {
xnln
~
0}
is
said
to
converge with order
p
~
1 to a point a if
Ia
- x I _<cia-
xniP
n+l
n~O
(2.0.13)
for some
c >
0.
If
p =
1,
the sequence
is
said
to
converge linearly to
a.
In
that case,
we
require c <
1;
the constant c
is
called the rate
of
linear convergence of x n to
a.
Using this definition, the earlier example (2.0.5)-(2.0.6) has order of conver-
gence 2, which
is
also called quadratic convergence. This definition of order
is
not
always a convenient one for some linearly convergent iterative methods.
Using
induction on (2.0.13) with p =
1,
we obtain
n=2:0
(2.0.14)
This shows directly the convergence
of
x"
to
a.
For some iterative methods
we
can
show
(2.0.14) directly, whereas (2.0.13) may not be true for any c <
1.
In such a
case, the method
will
still be said to converge linearly with a rate of
c.
2.1 The Bisection Method
Assume that
f(x)
is
continuous on a given interval [a,
b]
and that it also satisfies
f(a)f(b)
< 0
(2.1.1)
Using the
intermediat~
value Theorem
1.1
from Chapter
1,
the function
f(x)
must have
at
least one root in
[a,
b].
Usually
[a,
b]
is
chosen to contain only one
root
a,
but
the following algorithm for the bisection method will always converge
to some root
a
in
[a,
b], because of (2.1.1).
Algorithm
Bisect (J, a, b,root,
!)
1. Define c
•=
(a+
b)/2.
l.
If
b - c
~
!,
then accept root
•=
c,
and exit.
I
I
J
I
.I
~I
II
!1
THE
BISECTION METHOD
57
3.
If
sign(f(b))
·
sign(f(c))
s;
0, then
a:=
c;
otherwise, b
:=c.
4. Return to step
1.
The
interval
[a,
b] is halved in size for every pass through the algorithm.
Because
of
step 3,
[a,
b] will always contain a
root
of
f(x).
Since a root a
is
in
[a,
b],
it
must lie within either
[a,
c]
or
[c, b];
and
consequently
lc-
al
,::5;
b-
c =
c-
a
This is justification for the test in step
2.
On completion
of
the algorithm, c will
be
an approximation to the root with
lc-
al
,::5;
£
Example
Find
the largest real root a
of
f(
X)
=: x
6
- X -
1 = 0
(2.1.2)
It
is
.straightforward to show that 1 < a <
2,
and
we will use this as
our
initial
interval
[a,
b
].
The
algorithm Bisect was used with t:. = .00005. The results are
shown
in
Table 2.1. The first two iterates give
the
initial interval enclosing a, and
the remaining values
en,
n
;;::
1, denote the successive midpoints found using
Bisect.
The
final value c
15
= 1.13474 was accepted as
an
approximation to a with
Ia-
C1sl
s;
.00004.
The
true
solution is
a=
1.13472413840152 (2.1.3)
The
true
error
in
c
15
is
a - c
15
=.
- .000016
It
is much smaller than the predicted error bound.
It
might seem as though we
could have saved some computation by stopping with
an
earlier iterate. But there
Table 2.1 Example of bisection method
n
en
f(en) n
en
/(en)
2.0 = b 61.0
8
1.13672
.02062
1.0
=a
-1.0
9
1.13477
.00043
1
1.5
8.89063
10
1.13379
-.00960
2
1.25
1.56470
11
1.13428
-.00459
3 1.125
-.09771
12 1.13452 -.00208.
4
1.1875 .61665
13
1.13464
-.00083
5
1.15625
.23327 14 1.13470
-.00020
6
1.14063 .06158
15
1.13474 .00016
7 1.13281
-.01958

58
ROOTFINDING
FOR NONLINEAR EQUATIONS
is
no way to predict the possibly better accuracy in an earlier iterate, and thus
there
is
no way
we
can know the iterate
is
sufficiently accurate. For example, c
9
is
sufficiently accurate, but there
was
no way of telling that fact during the
computation.
To examine the speed of convergence, let
en
denote the
nth
value of c in the
algorithm. Then it
is
easy
to
see
that
a = limite"
n
.....
oo
(2.1.4)
where b - a denotes the length of the original interval input into Bisect. Using
the variant (2.0.14) for defining linear convergence,
we
say that the bisection
method converges linearly with a rate of
t.
The actual error may not decrease by
a factor
oft
at
each step, but the average rate of decrease
is
t,
based on (2.1.4).
The preceding example illustrates the result (2.1.4).
There are several deficiencies in the algorithm
Bisect. First, it does not take
account of the limits of machine precision,
as
described in Section 1.2 of Chapter
1.
A practical program would take account of the unit round on the machine [see
(1.2.12)], adjusting the given
t:
if
necessary. The second major problem with
Bisect
is
that it converges
very
slowly when compared with the methods defined
in the following sections. The major advantages of the bisection method are:
(1)
it
is
guaranteed to converge (provided f
is
continuous on [a, b] and (2.1.1)
is
satisfied), and (2) a reasonable error bound
is
available. Methods that at every
step giveJupper and lower bounds on the root
a are called enclosure methods. In
Section 2.8, we describe an enclosure algorithm that combines the previously
stated advantages of the bisection method with the faster convergence of the
secant method (described
in
Section 2.3).
2.2 Newton's Method
Assume that
an
initial estimate x
0
is
known for the desired root a of
f(x)·=
0.
Newton's method
will
produce a sequence of iterates { x": n 2 1
},
which
we
hope
will
converge to
a.
Since x
0
is
assumed close to a, approximate the graph of
y =
f(x)
in the vicinity of its root a by constructing its tangent line at
(x
0
,
/(x
0
)).
Then use the root of this tangent line to approximate a; call this new
approximation
x
1
•
Repeat this process, ad infinitum, to obtain a sequence of
iterates
x". As with the example (2.0.3) beginning this chapter, this leads to the
iteration formula
·
n20
(2.2.1)
The process
is
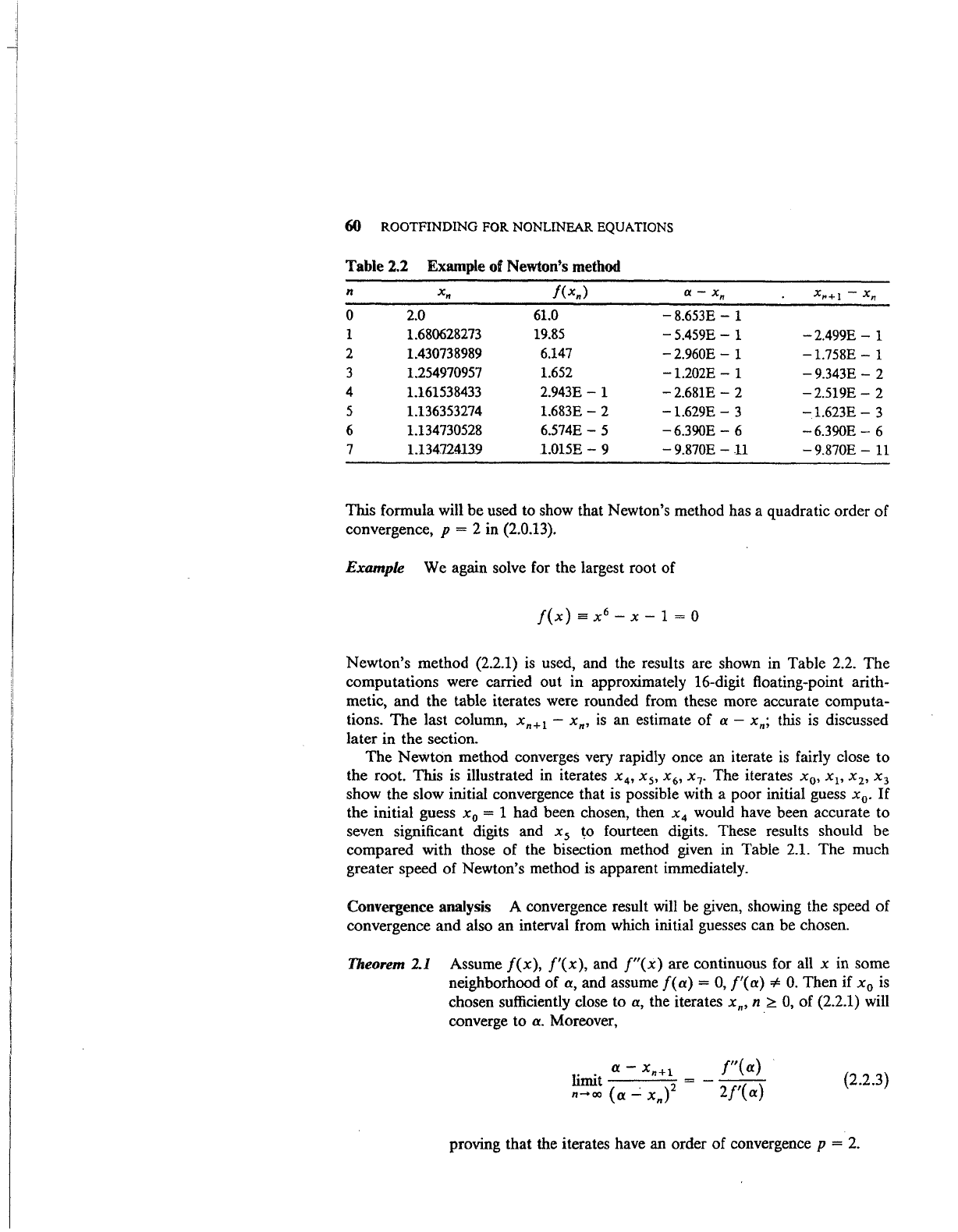
illustrated in Figure
2.2,
for the iterates x
1
and x
2
•

NEWTON'S METHOD 59
Figure
2.2 Newton's method.
Newton's method
is
the best known procedure for finding the roots of an
equation.
It
has been generalized
in
many
ways
for the solution of other, more
difficult nonlinear problems, for example, systems of nonlinear equations and
nonlinear integral and differential equations. It
is
not always the best method for
a given problem, but its formal simplicity and its great speed often lead it to be
the first method that people use in attempting to solve a nonlinear problem.
As another approach
to
(2.2.1),
we
use
a Taylor series development.
Ex-
panding
f(x)
about
xn,
with
~
between x and
xn.
Letting x
=a
and using
f(a)
=
0,
we
solve for a to
obtain
f(xJ
(a-
xJ
2
f"(~n)
a=x
----
n f'(xn)
·---
2 f'(xn)
with
~n
between
xn
and a.
We
can drop the error term (the last term) to obtain a
better approximation to
a than
xn,
and
we
recognize this approximation
as
xn+I
from (2.2.1). Then
n~O
(2.2.2)
60 ROOTFINDING FOR NONLINEAR EQUATIONS
Table 2.2
Example of Newton's method
n
Xn
f(x")
a -
xn
x"+J
-
xn
0 2.0
61.0
-8.653E-
1
1
1.680628273
19.85
-
5.459E-
1
-2.499E-
1
2 1.430738989
6.147
-2.960E-
1
-1.758E-
1
3
1.254970957
1.652
-1.202E-
1
-9.343E-
2
4
1.161538433
2.943E-
1
-2.681E-
2
-2.519E-
2
5
1.136353274
1.683E-
2
-1.629E-
3
-1.623E-
3
6
1.134730528
6.574E-
5
-6.390E-
6
-6.390E-
6
7
1.134724H9
1.015E-
9
-9.870E-
11
-9.870E-
11
This formula will be used to show that Newton's method has a quadratic order of
convergence,
p = 2 in (2.0.13).
Example We again solve for the largest root of
f(x)
= x
6
-
x - 1 = 0
Newton's method (2.2.1)
is
used, and the results are shown in Table 2.2. The
computations were carried out in approximately 16-digit floating-point arith-
metic, and the table iterates were rounded from these more accurate computa-
tions. The last column,
Xn+l
- Xn,
is
an estimate of
a-
xn;
this
is
discussed
later in the section.
The Newton method converges very rapidly once an iterate
is
fairly close to
the root. This
is
illustrated in iterates x
4
,
x
5
,
x
6
,
x
1
•
The iterates x
0
,
x
1
,
x
2
,
x
3
show the slow initial convergence that
is
possible with a poor initial guess x
0
•
If
the initial guess x
0
= 1 had been chosen, then x
4
would have been accurate to
seven significant digits and
x
5
~o
fourteen digits. These results should be
compared with those of the bisection method given in Table
2.1.
The much
greater speed of Newton's method
is
apparent immediately.
Convergence analysis A convergence result will be given, showing the speed
of
convergence and also an interval from which initial guesses can be chosen.
Theorem
2.1
Assume
f(x),
f'(x),
and
f"(x)
are continuous for all x in some
neighborhood of
a, and assume
/(a)=
0,
/'(ex)*
0.
Then if x
0
is
chosen sufficiently close to
a,
the iterates
xn,
n
~
0,
of (2.2.1) will
converge to
a.
Moreover, ·
a - x /"(a}
li
.
n+l
n~~
(a...:.
xJ
2
= -
2/'(cr.}
(2.2.3}
proving that the iterates have an order of convergence
p =
2.

NEWTON'S METHOD
61
Proof
Pick a sufficiently small interval
I=
[a
- t:,
a+
t:]
on which
f'(x)
=t-
0
[this exists by continuity of f'(x}], and then let
Max
lf"(x)
I
M =
.....::;.:XE=..!/'------
2 Min
l!'(x)
I
xe/
From (2.2.2),
Pick
Ia-
x
0
1
.::;;
t:
and
Mia-
x
0
1 < 1. Then
Mia-
x
1
1 < 1, and
Mia-
x
1
1
.::;;
Mia-
x
0
1,
which says
Ia-
x
1
1
.::;;
t:.
We
can apply the
same argument to x
1
,
x
2
,
.•.
, inductively, showing that
Ia-
xnl
.::;;
t:
and
Mia
- xnl < 1 for all n
:2:
1.
To show convergence,
use
(2.2.2)
to
give
(2.2.4)
and inductively,
(2.2.5)
Since
Mia
- x
0
1 <
1,
this
shows
that xn
~
a as n
~
oo.
In formula (2.2.2), the unknown point
~n
is between
xn
and a,
implying
~n
~
a
as
n
~
oo.
Thus
L
. .
a -
Xn+l
L"
.
_f_"(..:..._~_:_:_n:......)
lffilt
=
-.
lffilt-
n-+oo
(a
-.xn)
2
n-+oo
2f'(xn)
-f"(a)
2/'(
a)
•
The error column in Table 2.2 can be used to illustrate (2.2.3). In particular,
for that example,
f"(a)
-
2
/'{a)
=
-2.417
a - x
6
---'--2
=
-2.41
(a-x
5
)
Let M denote the limit on the right side of (2.2.2). Then if xn
is
near a, (2.2.2)
implies

62 ROOTFINDING FOR NONLINEAR EQUATIONS
y
X
Figure 2.3 The
Newton-Fourier
method.
In order to have convergence of
xn
to
o:,
this statement says that
we
should
probably have
1
Jo:-
xol
<-
M
(2.2.6)
Thus
M is a measure
of
how close x
0
must be chosen to
o:
to ensure convergence
to
o:.
Some examples with large values
of
Mare
given in the problems at the end
of
the chapter.
Another approach to the error analysis of Newton's method
is
given by the
following construction and theorem. Assume
f(x)
is
twice continuously differen-
tiable
on
an
interval
[a,
b]
containing
o:.
Further assume
f(a)
<
0,
f(b)
>
0,
and that
f'(x)>O
f"(x)>O
for a::;; x::;; b
(2.2.7)
Then
f(x)
is strictly increasing on
[a,
b],
and there
is
a unique root a in [a,
b].
Also,
f(x)
< 0 for a::;; x
<a,
and
f(x)
> 0 for a < x
::;;
b.
Let x
0
= b
and
define the Newton iterates
xn
as in (2.2.1). Next, define a new
sequence
of
iterates by
n
~
0
(2.2.8)
with
z
0
=
a.
The
resulting iterates are illustrated in Figure 2.3. With the use of
{
zn
},
we
obtain
excellent upper and lower bounds for a. The use of (2.2.8) with
Newton's
method
is called the
Newton-Fourier
method.
Theorem 2.2 As previously, assume
f(x)
is
twice continuously differentiable
on
[a,
b
],
f(
a)
<
0,
f(
b)
>
0,
and condition (2.2.
7).
Then the iterates
xn are strictly decreasing to
o:,
and the iterates z n are strictly
increasing to
o:.
Moreover,
X - Z
L
•
.
n+l
n+l
urut
2
n->oo
(xn-
zn)
f"(o:)
2f'(a)
(2.2.9)
showing that the distance between
xn
and
zn
decreases quadrati-
cally with
n.

NEWTON'S METHOD
63
Proof
We first show that
(2.2.10)
From
the definitions (2.2.1) and (2.2.8),
-[(xo)
x l -
Xo
=
-~-,
(-=-x-o-:-)-
< 0
-f(zo)
zl
-
Zo
=
-f-'(_x_o_)
> 0
From
the error formula (2.2.2),
Finally,
some
Zo
<
ro
< a
= ( _
)[f'(xo)
-
f'Uo)
l
0
a z
0
( ) >
f'
Xo
because
f'(x)
is
an increasing function
on
[a,
b
].
Combining these results
proves (2.2.10). This proof can be repeated inductively to prove that
n;;:=:O
(2.2.11)
The
sequence { x
n}
is bounded below
by
a,
and thus it has an infimum
.X;
similarly, the sequence { zn} has a supremum
z:
Limitxn =
X;;:::
a Limitzn = z
:$;
a
n-co
n-co
Taking limits in (2.2.1) and (2.2.8),
we
obtain
_ _
f(x)
- - f(Z)
x=x---
f'(x)
z=z---
f'(x)
which leads to
f(x)
= 0 = f(Z). Since a
is
the unique root of
f(x)
in
[a,
b
],
this proves { x
n}
and { z
n}
converge to a.
The
proof of (2.2.9) is more complicated, and
we
refer the reader to
Ostrowski (1973, p.
70). From Theorem
2.1
and formula (2.2.3), the

64
ROOTFINDING FOR NONLINEAR EQUATIONS
sequence { x"} converges
to
a quadratically. The result (2.2.9) shows that
lo:
-
Xnl
~
lzn
-
Xnl
is
an
error bound that decreases quadratically.
II
The hypotheses of Theorem 2.2 can be reduced to
/(x)
being twice ·continu-
ously differentiable in a neighborhood of
a and
/'(o:)f"(o:) * 0
(2.2.12)
From this, there will be an interval [a,
b]
about a with
f'(x)
and
f"(x)
nonzero
on the interval. Then the rootfinding problem
/(x)
= 0
will
satisfy (2.2.7) or it
can be easily modified
to
an equivalent problem that
will
satisfy
it.
For example,
if
/'(a)<
0, f"(o:) >
0,
then consider the rootfinding problem
g(x)
= 0 with
g(x)
=
f(
-x).
The root of g
will
be
-a,
and the conditions in (2.2.7)
will
be
satisfied by g(
x)
on some interval about
-a.
The numerical illustration of
Theorem
2.2
will
be left until the Problems section.
Error estimation The preceding procedure
gives
upper and lower bounds for
the root, with the distance
x"-
z"
decreasing quadratically. However, in most
applications, Newton's method
is
used alone, without (2.2.8).
In
that case,
we
use
the following.
Using the mean value theorem,
f(xJ
=
f(x")-
/(a)=
/'(~")(xn-
a)
-j(xn)
!'(~")
with
~n
between xn and a.
If
f'(x)
is not changing rapidly between
x"
and
o:,
then
we
have/'(~"),;,
f'(xn),
and
with the last equality following from the definition of Newton's method. For
Newton's method, the standard error estimate
is
(2.2.13)
and this
is
illustrated in Table 2.2. For relative error, use
a -
Xn
,;,
Xn+l
-
Xn
a xn+l
The Newton algorithm Using the Newton formula (2.2.1) and the error estimate
(2.2.13),
we
give the following algorithm.
