Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


THE
SECANT METHOD 65
Algorithm Newton
(f,
df,
x
0
,
t:, root, itmax, ier)
1.
Remark:
df
is
the derivative function
f'(x),
itmax
is
the
maximum number of iterates to be computed, and ier
is
an error
flag
to
the user.
2.
itnum
:=
1
3. denom
:=
df(x
0
).
4.
If
denom =
0,
then ier
:=
2 and exit.
5.
x
1
:=
x
0
-
/(x
0
)/denom
6.
If
lx
1
- x
0
1
~
t:, then set ier
:=
0, root
:=
x
1
,
and exit.
7.
If
itnum = itmax, set ier
:=
1 and exit.
8. Otherwise, itnum
:=
itnum +
1,
x
0
:=
x
1
,
and
go
to step
3.
As with the earlier algorithm Bisect, no account
is
taken of the limits of the
computer arithmetic, although a practical program would need to do such. Also,
Newton's method
is
not guaranteed to converge,
and
thus a test on the number of
iterates (step
7)
is
necessary.
When Newton's method converges, it generally does so quite rapidly, an
advantage over the bisection method. But again, it need not converge. Another
source of difficulty in some cases
is
the necessity of knowing
f'(x)
explicitly.
With some rootfinding problems, this
is
not possible. The method of the next
section remedies this situation, at the cost of a somewhat slower speed of
convergence.
2.3 The Secant Method
As with Newton's method, the graph of y =
f(x)
is
approximated by a straight
line in the vicinity of the root
a. In this case, assume that x
0
and x
1
are two
initial estimates of the root
a. Approximate the graph of y =
f(x)
by the secant
line
determined
by
(x
0
,
/(x
0
))
and
(x
1
,
f(x
1
)).
Let its root be denoted by x
2
;
we
hope it will be an improved approximation of a. This
is
illustrated in Figure 2.4.
Using the slope formula with the secant line,
we
have
Solving for x
2
,
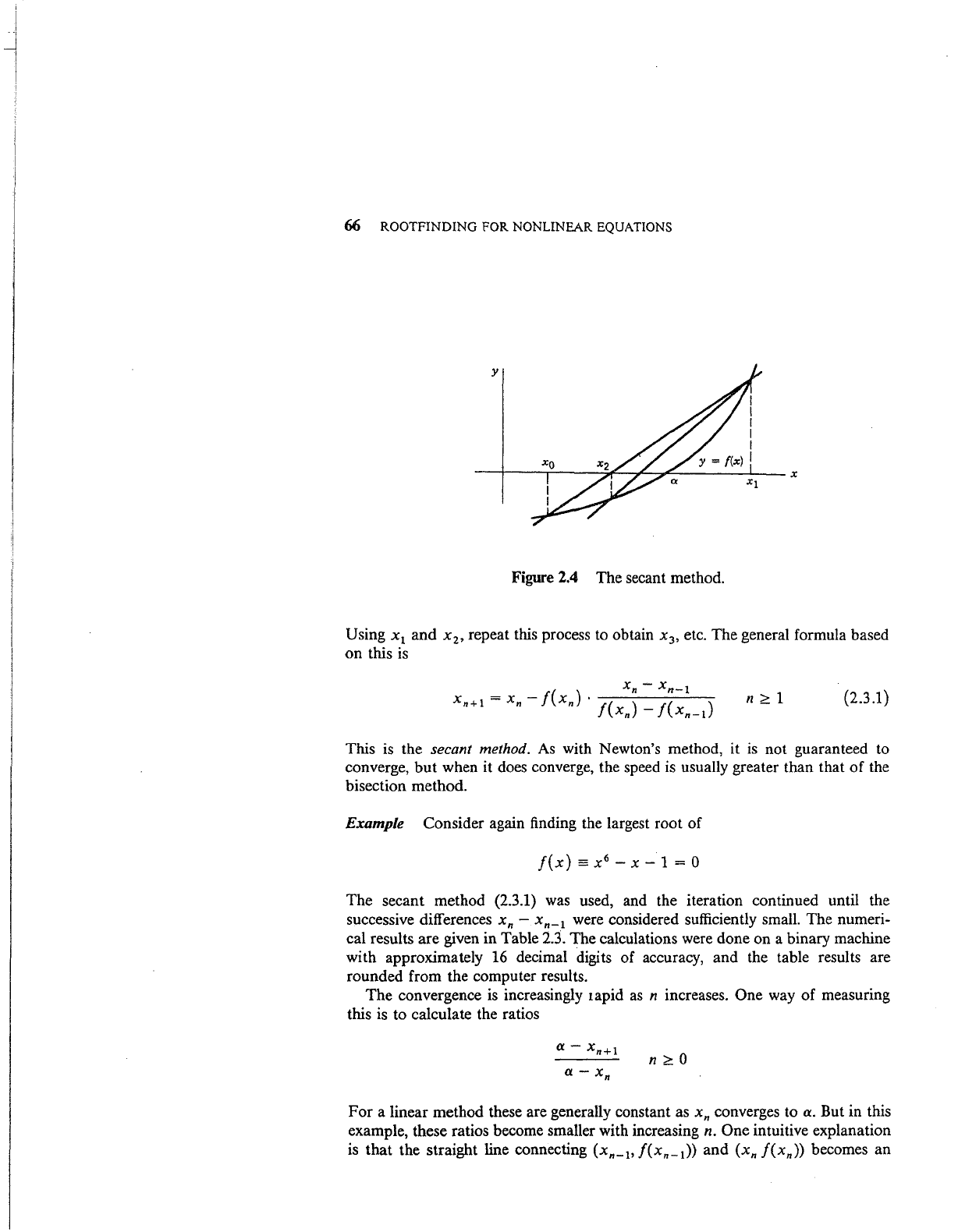
66 ROOTFINDING FOR NONLINEAR EQUATIONS
Figure 2.4 The secant method.
Using x
1
and x
2
,
repeat this process to obtain x
3
,
etc. The general formula based
on
this
is
n
~
1 (2.3.1)
This
is
the secant method.
As
with Newton's method, it
is
not guaranteed to
converge,
but
when it does converge, the speed
is
usually greater than that
of
the
bisection method.
Example Consider again finding the largest root of
f(x)
= x
6
-
x - 1 = 0
The secant method (2.3.1) was used, and the iteration continued until the
successive differences
xn-
xn_
1
were considered sufficiently small. The numeri-
cal results are given in Table 2.3. The calculations were done on a binary machine
with approximately
16
decimal digits of accuracy, and the table results are
rounded from the computer results.
The
convergence
is
increasingly rapid
as
n increases. One way of measuring
this is to calculate the ratios
n~O
For
a linear method these are generally constant as xn converges to a. But in this
example, these ratios become smaller with increasing
n.
One intuitive explanation
is
that the straight line connecting (xn_
1
,
f(xn_
1
))
and (xn
f(xn))
becomes an

THE
SECANT METHOD
67
Table 2.3 Example of secant method
n
X"
f(x")
a - x"
xn+l
-
xn
0 2.0
61.0
8.65E-
1
1
1.0
-1.0
1.35E-
1
1.61E-
2
2 1.016129032
-9.154E-
1
1.19E-
1
1.74E-
1
3 1.190577769
6.575E-
1
-5.59E-
2
-7.29E-
2
4
1.117655831
-1.685E-
1
-1.71E-
2
1.49E-
2
5
1.132531550
-2.244E-
2
2.19E-
3
·2.29E-
3
6
1.134816808
9.536E-
4
-9.27E-5
-9.32E-
5
7 1.134723646
-5.066E-
6
4.92E-
7
4.92E-
7
9 1.134724138
-1.135E-
9
l.lOE-
10
l.lOE-
10
increasingly accurate approximation to the graph of y =
f(x)
in
the vicinity
of
x =
a,
and
consequently the root xn+l
~f
the straight line is an increasingly
improved estimate of a. Also note that the iterates
x"
move above and below the
root a in
an
apparently random fashion as n increases. An explanation of this
will come from the error formula (2.3.3) given below.
Error
analysis Multiply both sides
of
(2~3:1)
by
-1
and then add a to
both
sides, obtaining
The
right-hand side can be
manipulat~d
algebraically to obtain the formula
(2.3.2)
The
quantities
f[xn-l•
xn]
and
j[xn_
1
, xn,
a] are-first- and second-order Newton
divided differences, defined in (1.1.13) of Chapter 1. The reader should check
(2.3.2) by substituting from (1.1.13) and then simplifying. Using (1.1.14), formula
(2.3.2) becomes
(2.3.3)
with~"
between x"_
1
and x",
and
f" between xn_
1
,
x",
and
a.
Using this error
formula, we can examine the convergence
of
the secant method.
Theorem 2.3 Assume
f(x),
f'(x),
and
f"(x)
are continuous for all values of x
in some interval containing a, and assume
f'(
a)
-:#
0.
Then if the
initial guesses x
0
and x
1
are chosen sufficiently close to
a,
the
iterates
x"
o((2.3.1) will converge to a. The order
of
convergence
will be p =
(1
+
/5)/2
= 1.62.

I
J
68 ROOTFINDING FOR NONLINEAR EQUATIONS
Proof
For
the neighborhood
I=
[a - t:, a +
t:]
with some
t:
>
0,
f'(x)
=I=
0
everywhere on
I.
Then define
Max
if"(x)
I
M =
_.:;,:_XE=/:...._
__
_
2Minlf'(x)l
xel
Then for all x
0
,
x
1
E
[a
- t:, a +
t:],
using (2.3.3),
le2l
.S:
led · leolM,
Mle2l
.S:
Mle1l · Mleol
Further assume that x
1
and x
0
are so chosen that
Then
Mje
2
1 < 1 since
(2.3.4)
and thus x
2
E
[a
-
t:,
a +
t:}.
We
apply this argument inductively to
show that
xn
E
[a
-
t:,
a +
t:}
and Mien I
.S:
8 for n
;e:
2.
To
prove convergence and obtain the order of convergence, continue
applying (2.3.3) to get
For
(2.3.5)
Thus
n;e:l
(2.3.6)
with
q
0
= q
1
=
1.
This is a
Fibonacci
sequence
of numbers, and an

THE
SECANT METHOD 69
explicit formula can be given:
1
qn
=
..j5
[ron+l-
rt+l]
n~O
Thus
1 +
..j5
'o
=
---
= 1.618
2
1-
..j5
't
=
---
=
-.618
2
for large· n
(2.3.7)
(2.3 .8)
For example q
5
=
8,
and formula (2.3.8) gives 8.025. Returning to
(2.3.5),
we
obtain the error bound
1
l
e I <
-8q·
n-
M
n~O
(2.3.9)
with
qn
given by {2.3.7). Since
qn--+
oo
as n --+
oo,
we
have
xn
--+ a.
By doing a more careful derivation, we can actually show that the
order of convergence
is
p =
(1
+
..f5
)/2.
To simplify the presentation,
we
instead show that this
is
the rate
at
which the bound in (2.3.9)
decreases. Let
Bn
denote the upper bound in (2.3.9). Then
1
-/)qn+l
Bn+l
M
--
=
r-:..;...,---
=
M'o-ll)qn+l-roqn
B;a
[
~
]'".
l)'oq.
which implies an order of convergence p = r
0
=
(1
+
..f5
)/2.
A similar
result holds for the actual errors
en;
moreover,
L
..
len+tl
I
/"(a)
l(.,f5-l)/
2
liDlt
--
=
---
n->oo
len!'"
2/'(a)
(2.3.10)
•
The error formula (2.3.3) can be used
to
explain the oscillating behavior
of
the
iterates
xn
about the root a in the last example.
For
xn
and
xn-l
near to
a,
(2.3.3) implies
f"(a)
a-
xn+l
=
-(a-
xJ(a-
Xn-1)
•
2
/'(a)
(2.3.11)

70 ROOTFINDING FOR NONLINEAR EQUATIONS
The
sign
of
a -
xn+l
is determined from that of the previous two errors, together
with the sign
of/"(
a)//'(
a).
The
condition (2.3.4) gives some information on how close the initial values x
0
and
x
1
should
be
to a in order to have convergence.
If
the quantity M is large, or
more specifically,
if
I
!J!ll
2/'(a)
is very large, then a - x
0
and a - x
1
must be correspondingly smaller. Conver-
gence can occur without (2.3.4),
but
it is likely to initially
be
quite haphazard in
such a case.
For
an
error test, use the same error estimate (2.2.13) that
was
used with
Newton's method, namely
Its use is illustrated in Table 2.3 in the last example. Because the secant method
may
not
converge, programs implementing it should have an upper limit on the
number
of
iterates,
as
with the algorithm Newton in the last section.
A possible problem with the secant method is the calculation of the approxi-
mate
derivative
a =
n
where the secant method (2.3.1)
is
then written
(2.3.12)
(2.3.13)
The
calculation
of
an involves loss of significance errors, in both the numerator
and
denominator. Thus it
is
a less accurate approximation of the derivative of f
as
xn
~
a. Nonetheless,
we
continue to obtain improvements in the accuracy of
xn,
until we approach the noise level of
f(x)
for x near a.
At
that point,
an
may
become very different from
f'(a),
and
xn+l
can
jump
rapidly away from the
root.
For
this reason, Dennis and Schnabel (1983, pp. 31-32) recommend the use
of
(2.3.12) until
xn
-xn-I
becomes sufficiently small. They then-recommend
another approximation of
f'(x):
with a fixed
h.
For
h,
they recommend
where
Ta
is a reasonable nonzero approximation to a, say
xn,
and 8
is
the

THE
SECANT METHOD
71
computer's unit round [see (1.2.12)]. They recommend the use of h .when
lx,-
x,_d
is
smaller than
h.
The cost of the secant method in function
evaluations
will rise slightly, but probably by not more than one
or
two.
The secant method
is
well
recommended as
an
efficient and easy-to-use
rootfinding procedure for a wide variety
of
problems.
It
also has the advantage of
not
requiring a knowledge of
f'(x),
unlike Newton's method.
In
Section
2.8,
the
secant method
will form
an
important
part
of another rootfind.ing algorithm that
is guaranteed to converge.
Comparison of Newton's rnetbod
and
the
secant method Newton's method and
the secant method are closely related.
If
the approximation
is used
in the Newton formula (2.2.1), we obtain the secant formula (2.3.1). The
conditions for convergence are almost the same [for example, see (2.2.6) and
(2.3.4) for conditions on the initial error], and the error formulas are similar [see
"(2.2.2)
and
(2.3.3)]. Nonetheless, there are two major differences. Newton's
method-requires-two function evaluations per iterate, that
of
f(x,)
and
f'(x,),
whereas the secant method requires only one function evaluation per iterate, that
of
f(x,.)
[provided the needed function value
f(x,_
1
)
is retained from the last
iteration]. Newton's method
is
generally more expensive per iteration. On the
other hand, Newton's method converges more rapidly [order
p = 2
vs.
the secant
method's
p = 1.62], and consequently it will require fewer iterations to attain a
given desired accuracy.
An
analysis of the effect
of
these two differences in the
secant and Newton methods
is
given below.
We now consider the expenditure of time necessary to reach a desired root a
within
a desired tolerance of t:.
To
simplify the analysis, we assume that the
initial guesses are quite close to the desired root. Define
xn+l
n;:::O
·and
let x
0
= x
0
•
We define
.X
1
based on the following convergence formula. From
(2.2.3) and
(2.3.10), respectively,
l
f"(a)
I
n
~
0, c =
2
/'(
a)
r=
1 +
v'5
2

72 ROOTFINDING FOR NONLINEAR EQUATIONS
Inductively for the error
in
the Newton iterates,
1 2"
Ia-
xnl
=
-(cia-
Xol)
c
n~O
Similarly for the secant method iterates,
~
d1+r+
...
+r"-11 - I'"
-
a-
x
0
Using the formula (1.1.9) for a finite geometric series,
we
obtain
d1+r+
...
+r•-l
=
d(r"-1)/(r-1)
=
c'"-1
and thus
To satisfy
Ia
-
xnl
~£,for
the Newton iterates,
we
must have
K
n>--
- log2
2"
(cia-
x
0
1)
~
Cf.
K=
log
[
log
EC ]
log
cia-
x
0
1
Let m be the time to evaluate
f(x),
and let s · m be the time to evaluate
f'(x).
Then the minimum time to obtain the desired accuracy with Newton's method
is
(1
+
s)mK
TN=
(m
+ ms)n = log2
(2.3.14)
For
the secant method, a similar calculation shows that
Ia
-
.Xnl
~
£ if
K
n>--
-
logr
Thus the minimum time necessary to obtain the desired accuracy
is
mK
T.
= mn =
--
s
logr
(2.3.15)

MULLER'S METHOD
73
To compare the times for the secant method
and
Newton's method,
we
have
The secant method
is
faster than the Newton method if the ratio
is
less than one,
log
2
s >
---1
= .44
log r
(2.3.16)
If
the time to evaluate
f'(x)
is
more than
44
percent of that necessary to evaluate
f(x),
then the secant method
is
more efficient.
In
practice, many other factors
will affect the relative costs of the two methods, so that the .44 factor should be
used with caution.
The preceding argument
is
useful in illustrating that the mathematical speed of
convergence
is~noUhe
complete picture. Total computing time, ease
of
use-of an
algorithm, stability, and other factors also have a bearing on the relative
desirability of one algorithm over another one.
2.4
Muller's Method
Muller's method
is
useful for obtaining both real and complex roots
of
a
function,
and
it
is
reasonably straightforward to implement as a computer
program. We derive it, discuss its convergence,
and
give some numerical exam-
ples.
Muller's method
is
a generalization of the approach that led to the secant
method. Given three points
Xo,
xl, Xz, a quadratic polynomial
is
constructed that
passes through the three points
(x;. f(x;)), i = 0,
1,
2;
one of the roots of this
polynomial is used
as
an improved estimate for a root a of
f(x).
The quadratic polynomial
is
given by
p(x)
=
f(x
2
)
+
(x-
x
2
)/[x
2
,
x
1
]
+
(x-
x
2
)(x-
x
1
)/[x
2
,
x
1
,
x
0
].
(2.4.1)
The divided differences
f[x
2
,
xd
and
f[x
2
,
x
1
,
x
0
]
were defined in (1.1.13) of
Chapter 1. To check that
p(x;)
=
f(x;)
i =
0,1,2
just substitute
X;
into (2.4.1) and then reduce the resulting expression using
(1.1.13). There are other formulas for
p(x)
given in Chapter
3,
but
the form
shown in
(2.4.1)
is
the most convenient for defining Muller's method. The

74
ROOTFINDING FOR NONLINEAR EQUATIONS
formula (2.4.1) is called Newton's divided difference form of the interpolating
polynomial, and it
is
developed in general in Section 3.2 of Chapter
3.
To
find the zeros oi (2.4.1)
we
first rewrite it in the more convenient form
y =
/(x
2
)
+
w(x-
x
2
)
+
f[x
2
,
x
1
,
x
0
]](x-
x
2
)
2
w =
/[x
2
,
x
1
]
+
(x
2
-
x
1
)/[x
2
,
x
1
,
x
0
]
=
/[x
2
,
x
1
]
+
/[x
2
,
x
0
]
-
J[x
0
,
x
1
]
We want to find the smallest value of x - x
2
that satisfies the equation y = 0,
thus finding the root of (2.4.1) that
is
closest to x
2
•
The solution
is
-w
±
/w
2
-
4f(x
2
)/[x
2
,
x
1
,
x
0
]
2f[x
2
,
x
1
,
x
0
]
with the sign chosen
to
make the numerator
as
small
as
possible. Because of the
loss-of-significance errors implicit in this formula,
we
rationalize the numerator
to obtain the new iteration formula
(2.4.2)
J
with the sign chosen
to
maximize the magnitude of the denominator.
Repeat (2.4.2) recursively
to
define a sequence of iterates {
xn:
n
:2::.
0}.
If
they
converge to a point
a, and if
['(a)
:1=
0, then a
is
a root of
f(x).
To
see
this, use
(1.1.14)
of
Chapter 1 and (2.4.2) to
give
w
~
f'(a)
as
n
~
co
2/(a)
a = a -
----;::=========-
['(a:)±
V[f'(a)]
2
-
2/(a)f"(a:)
showing that the right-hand fraction must be zero. Since
/'(a)
:1=
0 by assump-
tion, the method of choosing the sign in the denominator implies that the
denominator is nonzero. Then the numerator must be zero, showing
/(a)=
0.
The
assumption
/'(a)
:1=
0
will
say that a
is
a simple root.
(See
Section 2.7 for a
discussion
of
simple and multiple roots.)
By
an argument similar
to
that used for the secant method, it can be shown
that
..
Ia-
xn+ti lt(3>(a)
l<p-1)/2
Ltmtt =
n-+oo
Ia-
xnlp
6f'(a)
p
~
1.84 (2.4.3)
provided
f(x)
is three times continuously differentiable in a neighborhood
of
a
