Atkinson K. An Introduction to Numerical Analysis
Подождите немного. Документ загружается.


ROOTS
OF
POLYNOMIALS
95
Location theorems Because
p(x)
is a polynomial, many results can be given
about the roots of
p(x),
results that are not true for other functions. The best
known of these
is
the fundamental theorem
of
algPbra, which allows
us
to write
p(x)
as a unique product (except for order) involving the roots
(2.9.2)
and z
1
,
•••
,
zn
are the roots of
p(x),
repeated according to their multiplicity.
w_e
now give some classical results on locating and bounding these roots.
Descartes's rule
of
signs
is
used to bound the number of positive real roots of
p(x),
assuming the coefficients a
0
,
..•
,
an
are all real.
Let
v be the number of changes of sign
in
the coefficients of
p(x)
in (2.9.1),
ignoring the zero terms. Let k denote the number of positive real roots of
p(x
), counted according to their multiplicity. Then k
~
v and v - k
is
even.
A proof of this
is
given in Henrici (1974,
p.
442)
and
Householder (1970,
p.
82).
Example The expression
p(x)
= x
6
-
x-
1 has v = 1 changes of sign. There-
fore,
k = 1; otherwise, k =
0,
and v - k = 1
-is
not-an
-even-integer, a contradic-
tion.
Descartes's rule of signs can also be used to bound the number of negative
roots of
p(x).
Apply it to the polynomial
q(."~")
=
p(-x)
Its positive roots are the negative roots of
p(x).
Applying this to the last
example,
q(x)
= x
6
+
x-
1.
Again there
is
one positive real root [of
q(x)],
and
thus one negative real root of
p(x).
An upper bound for all of the roots of
p(x)
is
given by the following:
(2.9.3)
This is due to Augustin Cauchy, in 1829, and a proof
is
given
in
Householder
(1970, p.
71).
Another such result of Cauchy
is
based on considering the
polynomials
(2.9
.4)
(2.9.5)
Assume that a
0
=I=
0,
which
is
equivalent to assuming x = 0
is
not a root of
p(x).
Then by Descartes's law of signs, each of these polynomials has exactly one
positive root; call them
p
1
and p
2
,
respectively. Then all roots
zj
of
p(x)
satisfy
(2.9.6)

96 ROOTFINDING FOR NONLINEAR EQUATIONS
The
proof
of
the upper
bound
is given in Henrici (1974, p. 458)
and
Householder
(1970,
p.
70).
The
proof
of
the lower
bound
can
be
based
on
the following
approach,
which
can
also
be
used in constructing a lower
bound
for (2.9.3).
Consider
the
polynomial
a
0
=F
0 (2.9.7)
Then
the
roots
of
g(x)
are
1/z,
where z is a
root
of
p(x).
If
the upper
bound
result
of
(2.9.6) is.applied to (2.9.7), the lower
bound
result
of
(2.9.6) is obtained.
We
leave-this··application to
be
shown
in
a ·problem.
Because
each
of
the polynomials (2.9.4), (2.9.5) has a single simple positive
root,
Newton's
method
can
be
easily used to construct R
1
and
R
2
•
As
an
initial
guess,
use
the
upper
bound
from (2.9.3)
or
experiment with smaller positive
initial guesses.
We
leave the illustration
of
these results
to
the problems.
There
are
many
other results
of
the preceding type,
and
both
Henrici (1974,
chap.
6)
and
Householder (1970) wrote excellent treatises
on
the subject.
Nested
multiplication A very efficient way to evaluate the polynomial
p(x)
given
in
(2.9.1) is
to
use nested multiplication:
p(x)
= a
0
+
x(a
1
+
x(a
2
+ · · ·
+x(an_
1
+
anx)
· ·
·)
(2.9.8)
With
formula
(2.9.1), there are n additions
and
2n
- 1 multiplications,
and
with
(2.9 .8)
there
are
n additions
and
n multiplications, a considerable saving.
For
later
work, it is convenient to introduce the following auxiliary coeffi-
cients.
Let
bn
=a",
k=n-1,n-2,
...
,0
By
considering
(2.9.8),
it
is easy to see
that
p(z)
= b
0
Introduce
the
polynomial
Then
b
0
+
(x-
z)q(x)
= b
0
+
(x-
z)[b
1
+ b
2
x + · · ·
+bnx"-
1
]
=
(b
0
-
b
1
z) +
(b
1
-
b
2
z)x
+ · · ·
+{bn-1-
bnz}xn-1
+ bnx"
= a
0
+ a
1
x + ·
·.·
+anx"
=
p(x)
p(x)
= b
0
+
(x-
z)q(x)
(2.9.9)
(2.9.10)
(2.9.11)
(2.9.12)

ROOTS
OF
POLYNOMIALS 97
where
q(x)
is
the quotient and b
0
the remainder when
p(x)
is
divided
by
x -
z.
The use of (2.9.9) to evaluate
p(z)
and
to
form
the quotient polynomial
q(x)
is
also called
Horner's
method.
If
z is a root of
p(x),
then b
0
= 0 and
p(x)
=
(x-
z)q(x).
To
find
additional roots of
p(x),
we
can restrict our search to the roots of
q(x).
This
reduction process
is
called deflation; it must
be
used with some caution, a point
we
will return to later.
Newton's method
If
we
want to apply Newton's method to
find
a root of
p(x),
we
must be able to evaluate both
p(x)
and
p'(x)
at any point
z.
From (2.9.12),
p'(x)
=
(x-
z)q'(x)
+
q(x)
p'(z)
=
q(z)
(2.9.13)
We use (2.9.10) and (2.9.13) in the following adaption of Newton's method
to
polynomial rootfinding.
Algorithm Polynew
(a,
n, x
0
,
t:,
itma:X,
root,
b,
ier)
1.
Remark: a
is
a vector of
coefficients~
-itmax the maximum
number of iterates
to
be computed, b the vector of coefficients
for the deflated polynomial, and ier an error indicator.
2.
itnum
:=
1
4.
Fork=
n
-1,
...
,1, bk
==
ak
+
zbk+I•
c
:=
bk +
zc
6.
If
c =
0,
ier
==
2 and exit.
7. x
1
==
x
0
-
b
0
jc
8.
If
jx
1
- x
0
l
::;:
t:, then ier
==
0,
root
==
x
1
,
and exit.
9.
If
itnum = itmax, then ier
==
1 and exit.
10.
Otherwise, itnum
==
itnum + 1, x
0
==
x
1
,
and
go
to step
3.
Stability problems There are many polynomials in which the roots are quite
sensitive to small changes in the coefficients. Some of these are problems with
multiple roots, and it
is
not surprising that these roots are quite sensitive
to
small
changes in the coefficients. But there are many polynomials with only simple
roots that appear to be well separated, and for which the roots are still quite
sensitive to small perturbations. Formulas are derived below that explain this
sensitivity, and numerical examples are
also
given.

98 ROOTFINDING FOR NONLINEAR EQUATIONS
For
the theory, introduce
and
define a perturbation of
p(x)
by
p(x;
t:)
=
p(x)
+ t:q(x)
(2.9.15)
Denote
the-zeros of
p(
x;
t:)
by z
1
(
t:
),
...
, z n (
t:
),
repeated according
to
their
multiplicity, and let
z
1
=
z/0),
i =
1,
...
, n, denote the corresponding n zeros of
p(x)
=
p(x;
E>).
It
is
well
known that the zeros of a polynomial are continuous
functions
of
the coefficients of the polynomial
[see,
for example, Henrici (1974,
p.
281)].
Cons~uently,
z/t:}
is
a continuous function of t:. What
we
want
to
determine is how rapidly the root
z/t:)
varies with
t:,
fort: near
0.
Example Define
p(x;
t:)
=
(x-
1)
3
-
t:
p(x)
=
(x-
1)
3
t:>O
Then the roots
of
p(x)
are z
1
= z
1
= z
3
=
1.
The roots of
p(x;
t:)
are
with w = }(
-1
+
i/3).
For
all three roots
of
p(x;
t:),
To
illustrate this, let
t:
=
.001.
Then
p(x;
e)
= x
3
-
3x
2
+ 3x -
1.001
which
is
a relatively small change in
p(x).
But for the roots,
a relatively large change in the roots
z
1
=
1.
We now give some more general estimates for z
1
(t:)-
z
1
.
Case
(1) z
1
is a simple root of
p(x),
and thus
p'(z)
=F
0.
Using the theory of
functions of a complex variable,
it
is
known that z /
t:)
can be written
as
a power
series:
00
zJ(t:)
=
zJ
+ L 'fl£1
(2.9.16)
1-1

ROOTS
OF
POLYNOMIALS 99
To
estimate
z/£)-
z
1
,
we
obtain a formula for the first term y
1
£ in the
series·.
To
begin, it
is
easy to
see
that
i'r
=
zf(O)
To
calculate zj(£), differentiate the identity
which holds for all sufficiently small
£..
We
obtain
p'(z/£))zf(£)
+ q(z/£)) +
£q'(z/t:))zJ(t:)
= 0
-q(z/t:))
Z I (
()
-
--r--:--:-r-'~--7---,--,...,.
1
-
p'(z/t:))
+
£q'(z/£))
Substituting
£.
=
0,
we
obtain
Returning to (2.9.16),
(2.9.17)
(2.9.18)
for some constants
£
0
> 0 and K >
0.
To estimate
z/£)
for small
t:,
we
use
(2.9.19)
The coefficient of
t:
determines
how
rapidly
z/t:)
changes relative to
t:;·
if it
is
large, the root z
1
is called ill-conditioned.
Case (2) z
1
has multiplicity m >
1.
By
using techniques related
to
those used in
1,
we
can obtain
(2.9.20)
for some
£
0
>
0,
K >
0.
There are m possible values
to
y
1
,
given
as
the m
complex roots of

J
I
I
,I
100 ROOTFINDING FOR NONLINEAR EQUATIONS
Exompk
Consider the simple polynomial
p(x)
=
(x-
1)(x-
2) · · ·
(x-
7)
+
13068x
-
5040
(2.9.21)
For
the perturbation, take
q(
x)
= x
6
£ = - .002
Then
for the root
zj
=
j,
p'(z)
= nu
-I)
l+j
From
(2.9.19), we have the estimate
(2.9.22)
The
numerical values
of
o(j)
are given in Table 2.16.
The
relative error in the
coefficient
of
x
6
is .002/28 = 7.1E - 5, but the relative errors in the roots are
much larger. In fact, the size of some of the perturbations
8())
casts doubt
on
the validity
of
using the linear estimate (2.9.22).
The
actual roots of
p(x)
+
£q(x)
are given in
Table
2.17, and they correspond closely to the predicted perturba-
tions.
The
major departure is in the roots for j = 5 and j =
6.
They are complex,
which was
not
predicted by the linear estimate (2.9.22).
In
these two cases, £ is
outside the radius of convergence of the power series (2.9.16), since the latter will
only have the real coefficients
1
Y
=
-z~'>(o)
I
..
/! J
obtained
from differentiating (2.9.17).
Table
2.16
Values of
8(j)
from (2.9.22)
j
1
2
3
4
5
6
7
8(})
2.78E-
6
-1.07E-
3
3.04E-
2
-2.28E-
1
6.51E-
1
-7.77E-
1
3.27E
-1

ROOTS
OF
POLYNOMIALS
101
Table 2.17 Roots of
p(x;
f.)
for (2.9.21)
j
zj(
£)
Z/£)-
z/0)
1 1.0000028
2.80E-
6
2 1.9989382
-1.06E-
3
3 3.0331253
3.31E-
2
4
3.8195692
-1.80E-
1
5
5.4586758
+ .54012578i
6 5.4586758 - .54012578i
7
7.2330128
2.33E-
1
We say
that
a polynomial whose roots are unstable with respect to small
relative changes in the coefficients is ill-conditioned. Many such polynomials
occur naturally in applications. The previous example should illustrate the
difficulty in detennining with only a cursory examination whether or not a
polynomial is ill-conditioned.
Polynomial deflation Another
problem~occurs
with deflation
of
a polynomial to
a lower degree polynomial, a process defined following (2.9.12). Since the zeros
will not
be
found exactly, the lower degree polynomial (2.9.11) found by
extracting the latest root
will
generally be in error in all of its coefficients. Clearly
from the past example, this can cause a significant perturbation in the roots for
some classes
of
polynomials. Wilkinson (1963) has analyzed the effects of
deflation
and
has recommended the following general strategy: (1) Solve for the
roots
of
smallest magnitude first, ending with those
of
largest size; (2) after
obtaining approximations to all roots, iterate again using the original polynomial
and
using the previously calculated values as initial guesses. A complete discus-
sion can be found in Wilkinson (1963, pp. 55-65).
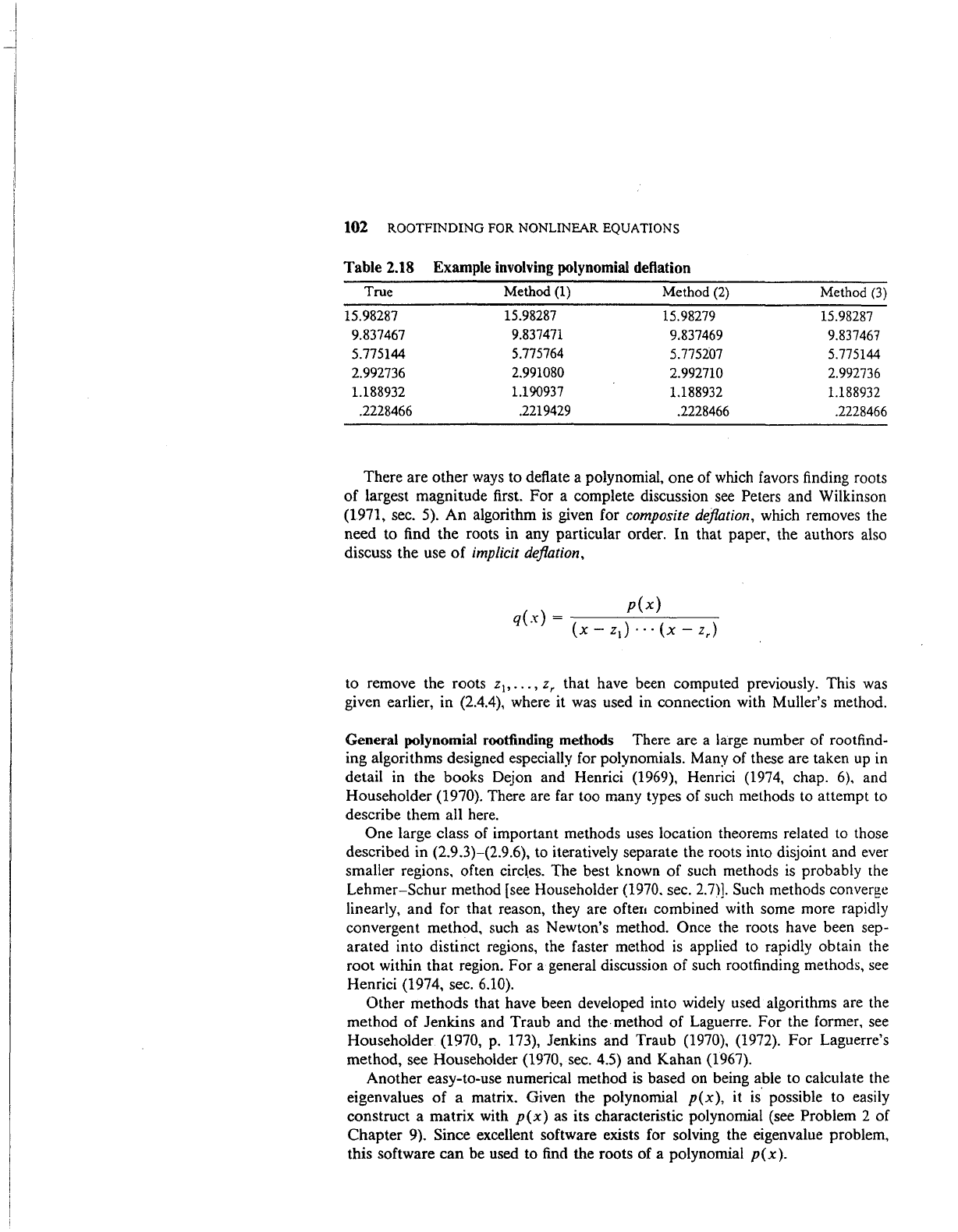
Example Consider finding the roots
of
the degree 6 Laguerre polynomial
p (
x)
= 720 - 4320x + 5400x
2
- 2400x
3
+ 450x
4
- 36x
5
+ x
6
The
Newton algorithm of the last section was used to solve for the roots, with
deflation following the acceptance of each new root.
The
roots were calculated in
two ways: (1) from largest to smallest, and (2) from smallest to largest. The
calculations were
in
single precision arithmetic
on
an
IBM 360,
and
the numeri-
cal results are given in Table 2.18. A comparison
of
the columns headed Method
(1)
and
Method (2) shows clearly the superiority
of
calculating the roots in the
order
of
in-::reasing magnitude.
If
the results of method (1) are used as initial
guesses for further iteration with the original polynomial, then approximate roots
are obtained with
an
accuracy better than that
of
method (2); see the column
headed Method (3) in the table. This table shows the importance
of
iterating
again with the original polynomial to remove the effects
of
the deflation process.
102 ROOTFINDING FOR NONLINEAR EQUATIONS
Table 2.18 Example involving polynomial deHation
True
Method
(1)
Method
(2)
15.98287
15.98287
15.98279
9.837467
9.837471
9.837469
5.775144
5.775764
5.775207
2.992736
2.991080
2.992710
1.188932
1.190937
1.188932
.2228466
.2219429
.2228466
Method
(3)
15.98287
9.837467
5.775144
2.992736
1.188932
.2228466
There are other
ways
to deflate a polynomial, one of which favors finding roots
of largest magnitude first. For a complete discussion
see
Peters and Wilkinson
(1971,
sec.
5).
An
algorithm
is
given for composite deflation, which removes the
need to find the roots in any particular order. In that paper, the authors also
discuss the use
of
implicit deflation,
to remove the roots z
1
,
•••
, z, that have been computed previously. This
was
given earlier, in (2.4.4), where it
was
used in connection with Muller's method.
General polynomial rootfinding methods There are a large number of rootfind-
ing algorithms designed especially for polynomials. Many of these are taken
up
in
detail
in
the books Dejon and Henrici (1969), Henrici (1974, chap. 6), and
Householder
(1970). There are far too many types of such methods
to
attempt to
describe them all
here.
One large class of important methods
uses
location theorems related
to
those
described in (2.9.3)-(2.9.6),
to
iteratively separate the roots into disjoint and ever
smaller regions, often
circl.es.
The best known
of
such methods
is
probably the
Lehmer-Schur method [see Householder
(1970. sec. 2.7)]. Such methods converge
linearly, and for that reason, they are ofteit combined with some more rapidly
convergent method, such
as
Newton's method. Once the roots have been sep-
arated into distinct regions, the faster method
is
applied
to
rapidly obtain the
root within that region. For a general discussion of such rootfinding methods,
see
Henrici (1974, sec. 6.10).
Other methods that have been developed into widely used algorithms are the
method of Jenkins and Traub and the method of Laguerre. For the former, see
Householder
(1970,
p.
173), Jenkins and Traub (1970), (1972). For Laguerre's
method, see Householder
(1970,
sec.
4.5) and Kahan (1967).
Another easy-to-use numerical method
is
based on being able to calculate the
eigenvalues
of
a matrix. Given the polynomial
p(x),
it
is.
possible to easily
construct a matrix with
p(x)
as
its characteristic polynomial (see Problem 2 of
Chapter 9). Since excellent software exists for solving the eigenvalue problem,
this software can be used to
find
the roots of a polynomial
p(x).

SYSTEMS
OF
NONLINEAR EQUATIONS 103
2.10 Systems of Nonlinear Equations
This section
and
the next are concerned with the numerical solution
of
systems
of
nonlinear equations in several variables. These problems are widespread in
applications,
and
they are varied in form. There is a great variety
of
methods for
the
solution
of
such systems, so
we
only introduce the subject.
We
give some
general theory and some numerical methods that are easily programmed.
To
do
a
complete development
of
the numerical analysis
of
solving nonlinear systems, we
would need a number of results from numerical linear algebra, which is not taken
up
until Chapters 7-9.
For
simplicity
of
presentation and ease
of
understanding,
the
theory
is
presented for only two equations:
(2.10.1)
The
generalization to n equations in n variables should be straightforward once
the
principal ideas have been grasped. As an additional aid, we will simulta-
neously consider the solution of
(2.10.1) in vector notation:
f(x)
= 0
X=
[~~]
(2.10.2)
The
solution
of
(2.10.1) can be looked upon as a two-step process: (1)
Find
the
zero curves
in
the x
1
x
2
-plane of the surfaces z = /
1
{x
1
,
x
2
)
and z = /
2
(x
1
,
x
2
),
and
(2) find the points
of
intersection
of
these zero curves in the x
1
x
2
-plane. This
perspective is used in the next section to generalize Newton's method to solve
(2.10.1).
Fixed-point theory We begin by generalizing some
of
the fixed-point iteration
theory
of
Section 2.5. Assume that the rootfinding problem (2.10.1) has been
reformulated in an equivalent form as
(2.10.3)
Denote
its solution by
We
study the fixed-point iteration
(2.10.4)
Using
vector notation, we write this as
xn+l =
g(xJ
(2.10.5)

104
ROOTFINDING
FOR NONLINEAR EQUATIONS
Table 2.19 Example (2.10.7) of fixed-point iteration
n
xl,n
x2,n
f1(Xl.n>
X2,n)
f2
( X1,
n'
X 2,
n)
0
-.5
.25
0.0
1.56E-
2
1
- .497343750
.254062500
2.43E-
4
5.46E-
4
2
-.497254194
.254077922
9.35E-
6
2.12E-
5
3
-
.497251343
.254078566
3.64E-
7
8.26E-
7
4 -.497251208
.254078592
1.50E-
8
3.30E-
8
with
Example Consider solving
/
1
=
3x?
+
4xi
- 1 = 0 /
2
=
x~
-
8xi
- 1 = 0
(2.10.6)
for the solution
a near
(x
1
, x
2
)
=
(-
.5,
.25). We solve this system iteratively with
[
xl,n+ll
=
[xl,n]-
[.016
x2,
n+
1
x2,
n .52
-.17][3x~.n
+
4x~.n-
1]
-.26
x2,n-8xl,n-1
(2.10.7)
The
origin
of
this reformulation
of
(2.10.6) is given later. The numerical results of
(2.10.7) are given in Table 2.19. Clearly the iterates are converging rapidly.
To
analyze the convergence of (2.10.5), begin by subtracting the two equations
in (2.10.4) from the corresponding equations
involving the
true
solution ct. Apply the mean value theorem for functions of two
variables (Theorem 1.5 with
n = 1) to these differences to obtain
for
i = 1,
2.
The
points
E~;)
=
(~{:>n,
~~:>n)
are on the line segment joining « and
xn.
In
matrix form, these error equations become
agl
(
E~
1
>)
agl
(
E~
1
>)
[«1-
xl,n+l]
=
axl
ax2
[
«1
-
xl,
n]
(2.10.8)
«2-
x2,n+l
og2 (
E~
2
>)
ag2(
E~
2
>)
a2-x2,n
oxl
ax2
